"Hec algorism' ars p'sens dicit' in qua
Talib; indor fruim bis quinq; figuris.[41]
fruim bis quinq; figuris.[41]
Title: The Hindu-Arabic Numerals
Author: David Eugene Smith
Louis Charles Karpinski
Release date: September 14, 2007 [eBook #22599]
Most recently updated: January 2, 2021
Language: English
Credits: Produced by David Newman, Chuck Greif, Keith Edkins and
the Online Distributed Proofreading Team at
https://www.pgdp.net (This file was produced from images
from the Cornell University Library: Historical Mathematics
Monographs collection.)
| Transcriber's note: | Sections in Greek or Hebrew will yield a transliteration when the pointer is moved over them, and words using diacritic characters in the Latin Extended Additional block, which may not display in some fonts or browsers, will display an unaccented version. |
BY
DAVID EUGENE SMITH
AND
LOUIS CHARLES KARPINSKI
BOSTON AND LONDON
GINN AND COMPANY, PUBLISHERS
1911
COPYRIGHT, 1911, BY DAVID EUGENE SMITH
AND LOUIS CHARLES KARPINSKI
ALL RIGHTS RESERVED
811.7
The Athenæum Press
GINN AND COMPANY · PROPRIETORS
BOSTON · U.S.A.
So familiar are we with the numerals that bear the misleading name of Arabic, and so extensive is their use in Europe and the Americas, that it is difficult for us to realize that their general acceptance in the transactions of commerce is a matter of only the last four centuries, and that they are unknown to a very large part of the human race to-day. It seems strange that such a labor-saving device should have struggled for nearly a thousand years after its system of place value was perfected before it replaced such crude notations as the one that the Roman conqueror made substantially universal in Europe. Such, however, is the case, and there is probably no one who has not at least some slight passing interest in the story of this struggle. To the mathematician and the student of civilization the interest is generally a deep one; to the teacher of the elements of knowledge the interest may be less marked, but nevertheless it is real; and even the business man who makes daily use of the curious symbols by which we express the numbers of commerce, cannot fail to have some appreciation for the story of the rise and progress of these tools of his trade.
This story has often been told in part, but it is a long time since any effort has been made to bring together the fragmentary narrations and to set forth the general problem of the origin and development of these [iv]numerals. In this little work we have attempted to state the history of these forms in small compass, to place before the student materials for the investigation of the problems involved, and to express as clearly as possible the results of the labors of scholars who have studied the subject in different parts of the world. We have had no theory to exploit, for the history of mathematics has seen too much of this tendency already, but as far as possible we have weighed the testimony and have set forth what seem to be the reasonable conclusions from the evidence at hand.
To facilitate the work of students an index has been prepared which we hope may be serviceable. In this the names of authors appear only when some use has been made of their opinions or when their works are first mentioned in full in a footnote.
If this work shall show more clearly the value of our number system, and shall make the study of mathematics seem more real to the teacher and student, and shall offer material for interesting some pupil more fully in his work with numbers, the authors will feel that the considerable labor involved in its preparation has not been in vain.
We desire to acknowledge our especial indebtedness to Professor Alexander Ziwet for reading all the proof, as well as for the digest of a Russian work, to Professor Clarence L. Meader for Sanskrit transliterations, and to Mr. Steven T. Byington for Arabic transliterations and the scheme of pronunciation of Oriental names, and also our indebtedness to other scholars in Oriental learning for information.
CHAPTER
PRONUNCIATION OF ORIENTAL NAMES vi
I. EARLY IDEAS OF THEIR ORIGIN 1
II. EARLY HINDU FORMS WITH NO PLACE VALUE 12
III. LATER HINDU FORMS, WITH A PLACE VALUE 38
IV. THE SYMBOL ZERO 51
V. THE QUESTION OF THE INTRODUCTION OF THE
NUMERALS INTO EUROPE BY BOETHIUS 63
VI. THE DEVELOPMENT OF THE NUMERALS AMONG THE ARABS 91
VII. THE DEFINITE INTRODUCTION OF THE NUMERALS INTO EUROPE 99
VIII. THE SPREAD OF THE NUMERALS IN EUROPE 128
INDEX 153
(S) = in Sanskrit names and words; (A) = in Arabic names and words.
b, d, f, g, h, j, l, m, n, p, sh (A), t, th (A), v, w, x, z, as in English.
a, (S) like u in but: thus pandit, pronounced pundit. (A) like a in ask or in man. ā, as in father.
c, (S) like ch in church (Italian c in cento).
ḍ, ṇ, ṣ, ṭ, (S) d, n, sh, t, made with the tip of the tongue turned up and back into the dome of the palate. ḍ, ṣ, ṭ, ẓ, (A) d, s, t, z, made with the tongue spread so that the sounds are produced largely against the side teeth. Europeans commonly pronounce ḍ, ṇ, ṣ, ṭ, ẓ, both (S) and (A), as simple d, n, sh (S) or s (A), t, z. ḏ (A), like th in this.
e, (S) as in they. (A) as in bed.
ġ, (A) a voiced consonant formed below the vocal cords; its sound is compared by some to a g, by others to a guttural r; in Arabic words adopted into English it is represented by gh (e.g. ghoul), less often r (e.g. razzia).
h preceded by b, c, t, ṭ, etc. does not form a single sound with these letters, but is a more or less distinct h sound following them; cf. the sounds in abhor, boathook, etc., or, more accurately for (S), the "bhoys" etc. of Irish brogue. h (A) retains its consonant sound at the end of a word. ḥ, (A) an unvoiced consonant formed below the vocal cords; its sound is sometimes compared to German hard ch, and may be represented by an h as strong as possible. In Arabic words adopted into English it is represented by h, e.g. in sahib, hakeem. ḥ (S) is final consonant h, like final h (A).
i, as in pin. ī, as in pique.
k, as in kick.
kh, (A) the hard ch of Scotch loch, German ach, especially of German as pronounced by the Swiss.
ṁ, ṅ, (S) like French final m or n, nasalizing the preceding vowel.
ṇ, see ḍ. ñ, like ng in singing.
o, (S) as in so. (A) as in obey.
q, (A) like k (or c) in cook; further back in the mouth than in kick.
r, (S) English r, smooth and untrilled. (A) stronger. ṛ, (S) r used as vowel, as in apron when pronounced aprn and not apern; modern Hindus say ri, hence our amrita, Krishna, for a-mṛta, Kṛṣṇa.
s, as in same. ṣ, see ḍ. ś, (S) English sh (German sch).
ṭ, see ḍ.
u, as in put. ū, as in rule.
y, as in you.
ẓ, see ḍ.
‛, (A) a sound kindred to the spiritus lenis (that is, to our ears, the mere distinct separation of a vowel from the preceding sound, as at the beginning of a word in German) and to ḥ. The ‛ is a very distinct sound in Arabic, but is more nearly represented by the spiritus lenis than by any sound that we can produce without much special training. That is, it should be treated as silent, but the sounds that precede and follow it should not run together. In Arabic words adopted into English it is treated as silent, e.g. in Arab, amber, Caaba (‛Arab, ‛anbar, ka‛abah).
(A) A final long vowel is shortened before al ('l) or ibn (whose i is then silent).
Accent: (S) as if Latin; in determining the place of the accent ṁ and ṅ count as consonants, but h after another consonant does not. (A), on the last syllable that contains a long vowel or a vowel followed by two consonants, except that a final long vowel is not ordinarily accented; if there is no long vowel nor two consecutive consonants, the accent falls on the first syllable. The words al and ibn are never accented.
EARLY IDEAS OF THEIR ORIGIN
It has long been recognized that the common numerals used in daily life are of comparatively recent origin. The number of systems of notation employed before the Christian era was about the same as the number of written languages, and in some cases a single language had several systems. The Egyptians, for example, had three systems of writing, with a numerical notation for each; the Greeks had two well-defined sets of numerals, and the Roman symbols for number changed more or less from century to century. Even to-day the number of methods of expressing numerical concepts is much greater than one would believe before making a study of the subject, for the idea that our common numerals are universal is far from being correct. It will be well, then, to think of the numerals that we still commonly call Arabic, as only one of many systems in use just before the Christian era. As it then existed the system was no better than many others, it was of late origin, it contained no zero, it was cumbersome and little used, [2]and it had no particular promise. Not until centuries later did the system have any standing in the world of business and science; and had the place value which now characterizes it, and which requires a zero, been worked out in Greece, we might have been using Greek numerals to-day instead of the ones with which we are familiar.
Of the first number forms that the world used this is not the place to speak. Many of them are interesting, but none had much scientific value. In Europe the invention of notation was generally assigned to the eastern shores of the Mediterranean until the critical period of about a century ago,—sometimes to the Hebrews, sometimes to the Egyptians, but more often to the early trading Phœnicians.[1]
The idea that our common numerals are Arabic in origin is not an old one. The mediæval and Renaissance writers generally recognized them as Indian, and many of them expressly stated that they were of Hindu origin.[2] [3]Others argued that they were probably invented by the Chaldeans or the Jews because they increased in value from right to left, an argument that would apply quite as well to the Roman and Greek systems, or to any other. It was, indeed, to the general idea of notation that many of these writers referred, as is evident from the words of England's earliest arithmetical textbook-maker, Robert Recorde (c. 1542): "In that thinge all men do agree, that the Chaldays, whiche fyrste inuented thys arte, did set these figures as thei set all their letters. for they wryte backwarde as you tearme it, and so doo they reade. And that may appeare in all Hebrewe, Chaldaye and Arabike bookes ... where as the Greekes, Latines, and all nations of Europe, do wryte and reade from the lefte hand towarde the ryghte."[3] Others, and [4]among them such influential writers as Tartaglia[4] in Italy and Köbel[5] in Germany, asserted the Arabic origin of the numerals, while still others left the matter undecided[6] or simply dismissed them as "barbaric."[7] Of course the Arabs themselves never laid claim to the invention, always recognizing their indebtedness to the Hindus both for the numeral forms and for the distinguishing feature of place value. Foremost among these writers was the great master of the golden age of Bagdad, one of the first of the Arab writers to collect the mathematical classics of both the East and the West, preserving them and finally passing them on to awakening Europe. This man was Moḥammed the Son of Moses, from Khowārezm, or, more after the manner of the Arab, Moḥammed ibn Mūsā al-Khowārazmī,[8] a man of great [5]learning and one to whom the world is much indebted for its present knowledge of algebra[9] and of arithmetic. Of him there will often be occasion to speak; and in the arithmetic which he wrote, and of which Adelhard of Bath[10] (c. 1130) may have made the translation or paraphrase,[11] he stated distinctly that the numerals were due to the Hindus.[12] This is as plainly asserted by later Arab [6]writers, even to the present day.[13] Indeed the phrase ‛ilm hindī, "Indian science," is used by them for arithmetic, as also the adjective hindī alone.[14]
Probably the most striking testimony from Arabic sources is that given by the Arabic traveler and scholar Mohammed ibn Aḥmed, Abū 'l-Rīḥān al-Bīrūnī (973-1048), who spent many years in Hindustan. He wrote a large work on India,[15] one on ancient chronology,[16] the "Book of the Ciphers," unfortunately lost, which treated doubtless of the Hindu art of calculating, and was the author of numerous other works. Al-Bīrūnī was a man of unusual attainments, being versed in Arabic, Persian, Sanskrit, Hebrew, and Syriac, as well as in astronomy, chronology, and mathematics. In his work on India he gives detailed information concerning the language and [7]customs of the people of that country, and states explicitly[17] that the Hindus of his time did not use the letters of their alphabet for numerical notation, as the Arabs did. He also states that the numeral signs called aṅka[18] had different shapes in various parts of India, as was the case with the letters. In his Chronology of Ancient Nations he gives the sum of a geometric progression and shows how, in order to avoid any possibility of error, the number may be expressed in three different systems: with Indian symbols, in sexagesimal notation, and by an alphabet system which will be touched upon later. He also speaks[19] of "179, 876, 755, expressed in Indian ciphers," thus again attributing these forms to Hindu sources.
Preceding Al-Bīrūnī there was another Arabic writer of the tenth century, Moṭahhar ibn Ṭāhir,[20] author of the Book of the Creation and of History, who gave as a curiosity, in Indian (Nāgarī) symbols, a large number asserted by the people of India to represent the duration of the world. Huart feels positive that in Moṭahhar's time the present Arabic symbols had not yet come into use, and that the Indian symbols, although known to scholars, were not current. Unless this were the case, neither the author nor his readers would have found anything extraordinary in the appearance of the number which he cites.
Mention should also be made of a widely-traveled student, Al-Mas‛ūdī (885?-956), whose journeys carried him from Bagdad to Persia, India, Ceylon, and even [8]across the China sea, and at other times to Madagascar, Syria, and Palestine.[21] He seems to have neglected no accessible sources of information, examining also the history of the Persians, the Hindus, and the Romans. Touching the period of the Caliphs his work entitled Meadows of Gold furnishes a most entertaining fund of information. He states[22] that the wise men of India, assembled by the king, composed the Sindhind. Further on[23] he states, upon the authority of the historian Moḥammed ibn ‛Alī ‛Abdī, that by order of Al-Manṣūr many works of science and astrology were translated into Arabic, notably the Sindhind (Siddhānta). Concerning the meaning and spelling of this name there is considerable diversity of opinion. Colebrooke[24] first pointed out the connection between Siddhānta and Sindhind. He ascribes to the word the meaning "the revolving ages."[25] Similar designations are collected by Sédillot,[26] who inclined to the Greek origin of the sciences commonly attributed to the Hindus.[27] Casiri,[28] citing the Tārīkh al-ḥokamā or Chronicles of the Learned,[29] refers to the work [9]as the Sindum-Indum with the meaning "perpetuum æternumque." The reference[30] in this ancient Arabic work to Al-Khowārazmī is worthy of note.
This Sindhind is the book, says Mas‛ūdī,[31] which gives all that the Hindus know of the spheres, the stars, arithmetic,[32] and the other branches of science. He mentions also Al-Khowārazmī and Ḥabash[33] as translators of the tables of the Sindhind. Al-Bīrūnī[34] refers to two other translations from a work furnished by a Hindu who came to Bagdad as a member of the political mission which Sindh sent to the caliph Al-Manṣūr, in the year of the Hejira 154 (A.D. 771).
The oldest work, in any sense complete, on the history of Arabic literature and history is the Kitāb al-Fihrist, written in the year 987 A.D., by Ibn Abī Ya‛qūb al-Nadīm. It is of fundamental importance for the history of Arabic culture. Of the ten chief divisions of the work, the seventh demands attention in this discussion for the reason that its second subdivision treats of mathematicians and astronomers.[35]
The first of the Arabic writers mentioned is Al-Kindī (800-870 A.D.), who wrote five books on arithmetic and four books on the use of the Indian method of reckoning. Sened ibn ‛Alī, the Jew, who was converted to Islam under the caliph Al-Māmūn, is also given as the author of a work on the Hindu method of reckoning. Nevertheless, there is a possibility[36] that some of the works ascribed to Sened ibn ‛Alī are really works of Al-Khowārazmī, whose name immediately precedes his. However, it is to be noted in this connection that Casiri[37] also mentions the same writer as the author of a most celebrated work on arithmetic.
To Al-Ṣūfī, who died in 986 A.D., is also credited a large work on the same subject, and similar treatises by other writers are mentioned. We are therefore forced to the conclusion that the Arabs from the early ninth century on fully recognized the Hindu origin of the new numerals.
Leonard of Pisa, of whom we shall speak at length in the chapter on the Introduction of the Numerals into Europe, wrote his Liber Abbaci[38] in 1202. In this work he refers frequently to the nine Indian figures,[39] thus showing again the general consensus of opinion in the Middle Ages that the numerals were of Hindu origin.
Some interest also attaches to the oldest documents on arithmetic in our own language. One of the earliest [11]treatises on algorism is a commentary[40] on a set of verses called the Carmen de Algorismo, written by Alexander de Villa Dei (Alexandra de Ville-Dieu), a Minorite monk of about 1240 A.D. The text of the first few lines is as follows:
"Hec algorism' ars p'sens dicit' in qua
Talib; indor fruim bis quinq; figuris.[41]
fruim bis quinq; figuris.[41]
"This boke is called the boke of algorim or augrym after lewder use. And this boke tretys of the Craft of Nombryng, the quych crafte is called also Algorym. Ther was a kyng of Inde the quich heyth Algor & he made this craft.... Algorisms, in the quych we use teen figurys of Inde."
EARLY HINDU FORMS WITH NO PLACE VALUE
While it is generally conceded that the scientific development of astronomy among the Hindus towards the beginning of the Christian era rested upon Greek[42] or Chinese[43] sources, yet their ancient literature testifies to a high state of civilization, and to a considerable advance in sciences, in philosophy, and along literary lines, long before the golden age of Greece. From the earliest times even up to the present day the Hindu has been wont to put his thought into rhythmic form. The first of this poetry—it well deserves this name, being also worthy from a metaphysical point of view[44]—consists of the Vedas, hymns of praise and poems of worship, collected during the Vedic period which dates from approximately 2000 B.C. to 1400 B.C.[45] Following this work, or possibly contemporary with it, is the Brahmanic literature, which is partly ritualistic (the Brāhmaṇas), and partly philosophical (the Upanishads). Our especial interest is [13]in the Sūtras, versified abridgments of the ritual and of ceremonial rules, which contain considerable geometric material used in connection with altar construction, and also numerous examples of rational numbers the sum of whose squares is also a square, i.e. "Pythagorean numbers," although this was long before Pythagoras lived. Whitney[46] places the whole of the Veda literature, including the Vedas, the Brāhmaṇas, and the Sūtras, between 1500 B.C. and 800 B.C., thus agreeing with Bürk[47] who holds that the knowledge of the Pythagorean theorem revealed in the Sūtras goes back to the eighth century B.C.
The importance of the Sūtras as showing an independent origin of Hindu geometry, contrary to the opinion long held by Cantor[48] of a Greek origin, has been repeatedly emphasized in recent literature,[49] especially since the appearance of the important work of Von Schroeder.[50] Further fundamental mathematical notions such as the conception of irrationals and the use of gnomons, as well as the philosophical doctrine of the transmigration of souls,—all of these having long been attributed to the Greeks,—are shown in these works to be native to India. Although this discussion does not bear directly upon the [14]origin of our numerals, yet it is highly pertinent as showing the aptitude of the Hindu for mathematical and mental work, a fact further attested by the independent development of the drama and of epic and lyric poetry.
It should be stated definitely at the outset, however, that we are not at all sure that the most ancient forms of the numerals commonly known as Arabic had their origin in India. As will presently be seen, their forms may have been suggested by those used in Egypt, or in Eastern Persia, or in China, or on the plains of Mesopotamia. We are quite in the dark as to these early steps; but as to their development in India, the approximate period of the rise of their essential feature of place value, their introduction into the Arab civilization, and their spread to the West, we have more or less definite information. When, therefore, we consider the rise of the numerals in the land of the Sindhu,[51] it must be understood that it is only the large movement that is meant, and that there must further be considered the numerous possible sources outside of India itself and long anterior to the first prominent appearance of the number symbols.
No one attempts to examine any detail in the history of ancient India without being struck with the great dearth of reliable material.[52] So little sympathy have the people with any save those of their own caste that a general literature is wholly lacking, and it is only in the observations of strangers that any all-round view of scientific progress is to be found. There is evidence that primary schools [15]existed in earliest times, and of the seventy-two recognized sciences writing and arithmetic were the most prized.[53] In the Vedic period, say from 2000 to 1400 B.C., there was the same attention to astronomy that was found in the earlier civilizations of Babylon, China, and Egypt, a fact attested by the Vedas themselves.[54] Such advance in science presupposes a fair knowledge of calculation, but of the manner of calculating we are quite ignorant and probably always shall be. One of the Buddhist sacred books, the Lalitavistara, relates that when the Bōdhisattva[55] was of age to marry, the father of Gopa, his intended bride, demanded an examination of the five hundred suitors, the subjects including arithmetic, writing, the lute, and archery. Having vanquished his rivals in all else, he is matched against Arjuna the great arithmetician and is asked to express numbers greater than 100 kotis.[56] In reply he gave a scheme of number names as high as 1053, adding that he could proceed as far as 10421,[57] all of which suggests the system of Archimedes and the unsettled question of the indebtedness of the West to the East in the realm of ancient mathematics.[58] Sir Edwin Arnold, [16]in The Light of Asia, does not mention this part of the contest, but he speaks of Buddha's training at the hands of the learned Viṣvamitra:
"And Viswamitra said, 'It is enough,
Let us to numbers. After me repeat
Your numeration till we reach the lakh,[59]
One, two, three, four, to ten, and then by tens
To hundreds, thousands.' After him the child
Named digits, decads, centuries, nor paused,
The round lakh reached, but softly murmured on,
Then comes the kōti, nahut, ninnahut,
Khamba, viskhamba, abab, attata,
To kumuds, gundhikas, and utpalas,
By pundarīkas into padumas,
Which last is how you count the utmost grains
Of Hastagiri ground to finest dust;[60]
But beyond that a numeration is,
The Kātha, used to count the stars of night,
The Kōti-Kātha, for the ocean drops;
Ingga, the calculus of circulars;
Sarvanikchepa, by the which you deal
With all the sands of Gunga, till we come
To Antah-Kalpas, where the unit is
The sands of the ten crore Gungas. If one seeks
More comprehensive scale, th' arithmic mounts
By the Asankya, which is the tale
Of all the drops that in ten thousand years
Would fall on all the worlds by daily rain;
Thence unto Maha Kalpas, by the which
The gods compute their future and their past.'"
Thereupon Viṣvamitra Ācārya[61] expresses his approval of the task, and asks to hear the "measure of the line" as far as yōjana, the longest measure bearing name. This given, Buddha adds:
... "'And master! if it please,
I shall recite how many sun-motes lie
From end to end within a yōjana.'
Thereat, with instant skill, the little prince
Pronounced the total of the atoms true.
But Viswamitra heard it on his face
Prostrate before the boy; 'For thou,' he cried,
'Art Teacher of thy teachers—thou, not I,
Art Gūrū.'"
It is needless to say that this is far from being history. And yet it puts in charming rhythm only what the ancient Lalitavistara relates of the number-series of the Buddha's time. While it extends beyond all reason, nevertheless it reveals a condition that would have been impossible unless arithmetic had attained a considerable degree of advancement.
To this pre-Christian period belong also the Vedāṅgas, or "limbs for supporting the Veda," part of that great branch of Hindu literature known as Smṛiti (recollection), that which was to be handed down by tradition. Of these the sixth is known as Jyotiṣa (astronomy), a short treatise of only thirty-six verses, written not earlier than 300 B.C., and affording us some knowledge of the extent of number work in that period.[62] The Hindus [18]also speak of eighteen ancient Siddhāntas or astronomical works, which, though mostly lost, confirm this evidence.[63]
As to authentic histories, however, there exist in India none relating to the period before the Mohammedan era (622 A.D.). About all that we know of the earlier civilization is what we glean from the two great epics, the Mahābhārata[64] and the Rāmāyana, from coins, and from a few inscriptions.[65]
It is with this unsatisfactory material, then, that we have to deal in searching for the early history of the Hindu-Arabic numerals, and the fact that many unsolved problems exist and will continue to exist is no longer strange when we consider the conditions. It is rather surprising that so much has been discovered within a century, than that we are so uncertain as to origins and dates and the early spread of the system. The probability being that writing was not introduced into India before the close of the fourth century B.C., and literature existing only in spoken form prior to that period,[66] the number work was doubtless that of all primitive peoples, palpable, merely a matter of placing sticks or cowries or pebbles on the ground, of marking a sand-covered board, or of cutting notches or tying cords as is still done in parts of Southern India to-day.[67]
The early Hindu numerals[68] may be classified into three great groups, (1) the Kharoṣṭhī, (2) the Brāhmī, and (3) the word and letter forms; and these will be considered in order.
The Kharoṣṭhī numerals are found in inscriptions formerly known as Bactrian, Indo-Bactrian, and Aryan, and appearing in ancient Gandhāra, now eastern Afghanistan and northern Punjab. The alphabet of the language is found in inscriptions dating from the fourth century B.C. to the third century A.D., and from the fact that the words are written from right to left it is assumed to be of Semitic origin. No numerals, however, have been found in the earliest of these inscriptions, number-names probably having been written out in words as was the custom with many ancient peoples. Not until the time of the powerful King Aśoka, in the third century B.C., do numerals appear in any inscriptions thus far discovered; and then only in the primitive form of marks, quite as they would be found in Egypt, Greece, Rome, or in [20]various other parts of the world. These Aśoka[69] inscriptions, some thirty in all, are found in widely separated parts of India, often on columns, and are in the various vernaculars that were familiar to the people. Two are in the Kharoṣṭhī characters, and the rest in some form of Brāhmī. In the Kharoṣṭhī inscriptions only four numerals have been found, and these are merely vertical marks for one, two, four, and five, thus:
In the so-called Śaka inscriptions, possibly of the first century B.C., more numerals are found, and in more highly developed form, the right-to-left system appearing, together with evidences of three different scales of counting,—four, ten, and twenty. The numerals of this period are as follows:
There are several noteworthy points to be observed in studying this system. In the first place, it is probably not as early as that shown in the Nānā Ghāt forms hereafter given, although the inscriptions themselves at Nānā Ghāt are later than those of the Aśoka period. The [21]four is to this system what the X was to the Roman, probably a canceling of three marks as a workman does to-day for five, or a laying of one stick across three others. The ten has never been satisfactorily explained. It is similar to the A of the Kharoṣṭhī alphabet, but we have no knowledge as to why it was chosen. The twenty is evidently a ligature of two tens, and this in turn suggested a kind of radix, so that ninety was probably written in a way reminding one of the quatre-vingt-dix of the French. The hundred is unexplained, although it resembles the letter ta or tra of the Brāhmī alphabet with 1 before (to the right of) it. The two hundred is only a variant of the symbol for hundred, with two vertical marks.[70]
This system has many points of similarity with the Nabatean numerals[71] in use in the first centuries of the Christian era. The cross is here used for four, and the Kharoṣṭhī form is employed for twenty. In addition to this there is a trace of an analogous use of a scale of twenty. While the symbol for 100 is quite different, the method of forming the other hundreds is the same. The correspondence seems to be too marked to be wholly accidental.
It is not in the Kharoṣṭhī numerals, therefore, that we can hope to find the origin of those used by us, and we turn to the second of the Indian types, the Brāhmī characters. The alphabet attributed to Brahmā is the oldest of the several known in India, and was used from the earliest historic times. There are various theories of its origin, [22]none of which has as yet any wide acceptance,[72] although the problem offers hope of solution in due time. The numerals are not as old as the alphabet, or at least they have not as yet been found in inscriptions earlier than those in which the edicts of Aśoka appear, some of these having been incised in Brāhmī as well as Kharoṣṭhī. As already stated, the older writers probably wrote the numbers in words, as seems to have been the case in the earliest Pali writings of Ceylon.[73]
The following numerals are, as far as known, the only ones to appear in the Aśoka edicts:[74]
These fragments from the third century B.C., crude and unsatisfactory as they are, are the undoubted early forms from which our present system developed. They next appear in the second century B.C. in some inscriptions in the cave on the top of the Nānā Ghāt hill, about seventy-five miles from Poona in central India. These inscriptions may be memorials of the early Andhra dynasty of southern India, but their chief interest lies in the numerals which they contain.
The cave was made as a resting-place for travelers ascending the hill, which lies on the road from Kalyāna to Junar. It seems to have been cut out by a descendant [23]of King Śātavāhana,[75] for inside the wall opposite the entrance are representations of the members of his family, much defaced, but with the names still legible. It would seem that the excavation was made by order of a king named Vedisiri, and "the inscription contains a list of gifts made on the occasion of the performance of several yagnas or religious sacrifices," and numerals are to be seen in no less than thirty places.[76]
There is considerable dispute as to what numerals are really found in these inscriptions, owing to the difficulty of deciphering them; but the following, which have been copied from a rubbing, are probably number forms:[77]
The inscription itself, so important as containing the earliest considerable Hindu numeral system connected with our own, is of sufficient interest to warrant reproducing part of it in facsimile, as is done on page 24.
The next very noteworthy evidence of the numerals, and this quite complete as will be seen, is found in certain other cave inscriptions dating back to the first or second century A.D. In these, the Nasik[78] cave inscriptions, the forms are as follows:
From this time on, until the decimal system finally adopted the first nine characters and replaced the rest of the Brāhmī notation by adding the zero, the progress of these forms is well marked. It is therefore well to present synoptically the best-known specimens that have come down to us, and this is done in the table on page 25.[79]
| Numerals | 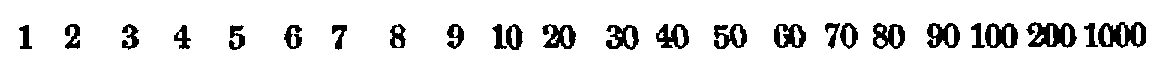 |
| Aśoka[80] |  |
| Śaka[81] |  |
| Aśoka[82] |  |
| Nāgarī[83] |  |
| Nasik[84] |  |
| Kṣatrapa[85] | 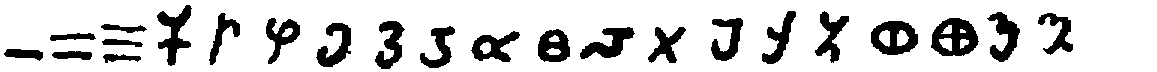 |
| Kuṣana[86] | 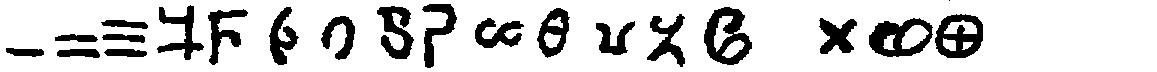 |
| Gupta[87] |  |
| Valhabī[88] |  |
| Nepal[89] | 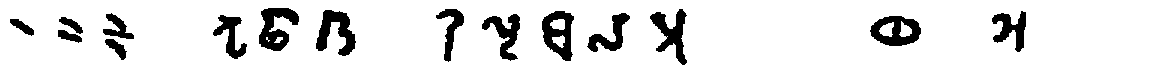 |
| Kaliṅga[90] |  |
| Vākāṭaka[91] | 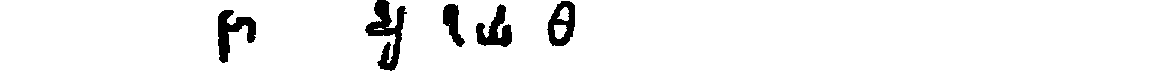 |
[Most of these numerals are given by Bühler, loc. cit., Tafel IX.]
With respect to these numerals it should first be noted that no zero appears in the table, and as a matter of fact none existed in any of the cases cited. It was therefore impossible to have any place value, and the numbers like twenty, thirty, and other multiples of ten, one hundred, and so on, required separate symbols except where they were written out in words. The ancient Hindus had no less than twenty of these symbols,[92] a number that was afterward greatly increased. The following are examples of their method of indicating certain numbers between one hundred and one thousand:
To these may be added the following numerals below one hundred, similar to those in the table:
We have thus far spoken of the Kharoṣṭhī and Brāhmī numerals, and it remains to mention the third type, the word and letter forms. These are, however, so closely connected with the perfecting of the system by the invention of the zero that they are more appropriately considered in the next chapter, particularly as they have little relation to the problem of the origin of the forms known as the Arabic.
Having now examined types of the early forms it is appropriate to turn
our attention to the question of their origin. As to the first three
there is no question. The 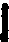 or
or  is
simply one stroke, or one stick laid down by the computer. The
is
simply one stroke, or one stick laid down by the computer. The  or
or 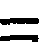 represents two
strokes or two sticks, and so for the
represents two
strokes or two sticks, and so for the 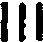 and
and 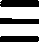 .
From some primitive
.
From some primitive  came
the two of Egypt, of Rome, of early Greece, and of various other
civilizations. It appears in the three Egyptian numeral systems in the
following forms:
came
the two of Egypt, of Rome, of early Greece, and of various other
civilizations. It appears in the three Egyptian numeral systems in the
following forms:
The last of these is merely a cursive form as in the Arabic 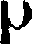 , which becomes our 2 if tipped
through a right angle. From some primitive
, which becomes our 2 if tipped
through a right angle. From some primitive  came the Chinese [28]symbol, which is
practically identical with the symbols found commonly in India from 150
B.C. to 700 A.D. In
the cursive form it becomes
came the Chinese [28]symbol, which is
practically identical with the symbols found commonly in India from 150
B.C. to 700 A.D. In
the cursive form it becomes  , and this was frequently used for two
in Germany until the 18th century. It finally went into the modern form
2, and the
, and this was frequently used for two
in Germany until the 18th century. It finally went into the modern form
2, and the 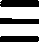 in
the same way became our 3.
in
the same way became our 3.
There is, however, considerable ground for interesting speculation with respect to these first three numerals. The earliest Hindu forms were perpendicular. In the Nānā Ghāt inscriptions they are vertical. But long before either the Aśoka or the Nānā Ghāt inscriptions the Chinese were using the horizontal forms for the first three numerals, but a vertical arrangement for four.[101] Now where did China get these forms? Surely not from India, for she had them, as her monuments and literature[102] show, long before the Hindus knew them. The tradition is that China brought her civilization around the north of Tibet, from Mongolia, the primitive habitat being Mesopotamia, or possibly the oases of Turkestan. Now what numerals did Mesopotamia use? The Babylonian system, simple in its general principles but very complicated in many of its details, is now well known.[103] In particular, one, two, and three were represented by vertical arrow-heads. Why, then, did the Chinese write [29]theirs horizontally? The problem now takes a new interest when we find that these Babylonian forms were not the primitive ones of this region, but that the early Sumerian forms were horizontal.[104]
What interpretation shall be given to these facts? Shall we say that it was mere accident that one people wrote "one" vertically and that another wrote it horizontally? This may be the case; but it may also be the case that the tribal migrations that ended in the Mongol invasion of China started from the Euphrates while yet the Sumerian civilization was prominent, or from some common source in Turkestan, and that they carried to the East the primitive numerals of their ancient home, the first three, these being all that the people as a whole knew or needed. It is equally possible that these three horizontal forms represent primitive stick-laying, the most natural position of a stick placed in front of a calculator being the horizontal one. When, however, the cuneiform writing developed more fully, the vertical form may have been proved the easier to make, so that by the time the migrations to the West began these were in use, and from them came the upright forms of Egypt, Greece, Rome, and other Mediterranean lands, and those of Aśoka's time in India. After Aśoka, and perhaps among the merchants of earlier centuries, the horizontal forms may have come down into India from China, thus giving those of the Nānā Ghāt cave and of later inscriptions. This is in the realm of speculation, but it is not improbable that further epigraphical studies may confirm the hypothesis.
As to the numerals above three there have been very many conjectures. The figure one of the Demotic looks like the one of the Sanskrit, the two (reversed) like that of the Arabic, the four has some resemblance to that in the Nasik caves, the five (reversed) to that on the Kṣatrapa coins, the nine to that of the Kuṣana inscriptions, and other points of similarity have been imagined. Some have traced resemblance between the Hieratic five and seven and those of the Indian inscriptions. There have not, therefore, been wanting those who asserted an Egyptian origin for these numerals.[105] There has already been mentioned the fact that the Kharoṣṭhī numerals were formerly known as Bactrian, Indo-Bactrian, and Aryan. Cunningham[106] was the first to suggest that these numerals were derived from the alphabet of the Bactrian civilization of Eastern Persia, perhaps a thousand years before our era, and in this he was supported by the scholarly work of Sir E. Clive Bayley,[107] who in turn was followed by Canon Taylor.[108] The resemblance has not proved convincing, however, and Bayley's drawings [31]have been criticized as being affected by his theory. The following is part of the hypothesis:[109]
| Numeral | Hindu | Bactrian | Sanskrit |
| 4 | 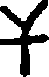 |  = ch = ch | chatur, Lat. quattuor |
| 5 | 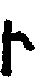 |  = p = p | pancha, Gk. πέντε |
| 6 | 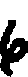 | 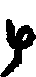 = s = s | ṣaṣ |
| 7 | 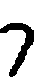 | 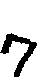 = ṣ = ṣ | sapta |
| (the s and ṣ are interchanged as occasionally in N. W. India) | |||
Bühler[110] rejects this hypothesis, stating that in four cases (four, six, seven, and ten) the facts are absolutely against it.
While the relation to ancient Bactrian forms has been generally doubted, it is agreed that most of the numerals resemble Brāhmī letters, and we would naturally expect them to be initials.[111] But, knowing the ancient pronunciation of most of the number names,[112] we find this not to be the case. We next fall back upon the hypothesis [32]that they represent the order of letters[113] in the ancient alphabet. From what we know of this order, however, there seems also no basis for this assumption. We have, therefore, to confess that we are not certain that the numerals were alphabetic at all, and if they were alphabetic we have no evidence at present as to the basis of selection. The later forms may possibly have been alphabetical expressions of certain syllables called akṣaras, which possessed in Sanskrit fixed numerical values,[114] but this is equally uncertain with the rest. Bayley also thought[115] that some of the forms were Phœnician, as notably the use of a circle for twenty, but the resemblance is in general too remote to be convincing.
There is also some slight possibility that Chinese influence is to be seen in certain of the early forms of Hindu numerals.[116]
More absurd is the hypothesis of a Greek origin, supposedly supported by derivation of the current symbols from the first nine letters of the Greek alphabet.[117] This difficult feat is accomplished by twisting some of the letters, cutting off, adding on, and effecting other changes to make the letters fit the theory. This peculiar theory was first set up by Dasypodius[118] (Conrad Rauhfuss), and was later elaborated by Huet.[119]
A bizarre derivation based upon early Arabic (c. 1040 A.D.) sources is given by Kircher in his work[120] on number mysticism.
He quotes from Abenragel,[121] giving the Arabic and a Latin
translation[122] and
stating that the ordinary Arabic forms are derived from sectors of a
circle,  .
.
Out of all these conflicting theories, and from all the resemblances seen or imagined between the numerals of the West and those of the East, what conclusions are we prepared to draw as the evidence now stands? Probably none that is satisfactory. Indeed, upon the evidence at [35]hand we might properly feel that everything points to the numerals as being substantially indigenous to India. And why should this not be the case? If the king Srong-tsan-Gampo (639 A.D.), the founder of Lhāsa,[123] could have set about to devise a new alphabet for Tibet, and if the Siamese, and the Singhalese, and the Burmese, and other peoples in the East, could have created alphabets of their own, why should not the numerals also have been fashioned by some temple school, or some king, or some merchant guild? By way of illustration, there are shown in the table on page 36 certain systems of the East, and while a few resemblances are evident, it is also evident that the creators of each system endeavored to find original forms that should not be found in other systems. This, then, would seem to be a fair interpretation of the evidence. A human mind cannot readily create simple forms that are absolutely new; what it fashions will naturally resemble what other minds have fashioned, or what it has known through hearsay or through sight. A circle is one of the world's common stock of figures, and that it should mean twenty in Phœnicia and in India is hardly more surprising than that it signified ten at one time in Babylon.[124] It is therefore quite probable that an extraneous origin cannot be found for the very sufficient reason that none exists.
Of absolute nonsense about the origin of the symbols which we use much has been written. Conjectures, [36]however, without any historical evidence for support, have no place in a serious discussion of the gradual evolution of the present numeral forms.[125]
 | |
| Siam |  |
| Burma[126] | 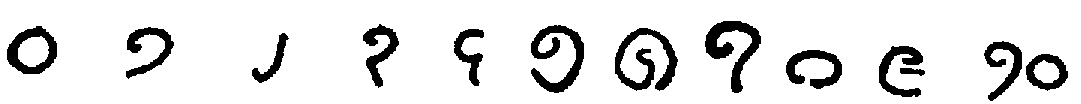 |
| Malabar[127] | 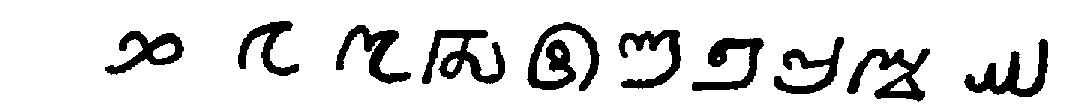 |
| Tibet[128] | 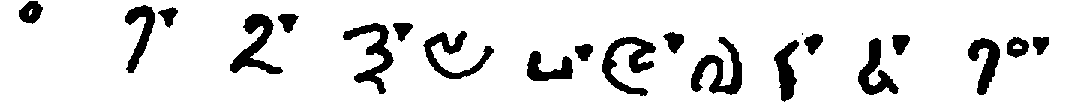 |
| Ceylon[129] | 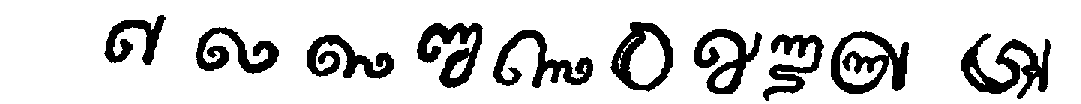 |
| Malayalam[129] |  |
We may summarize this chapter by saying that no one knows what suggested certain of the early numeral forms used in India. The origin of some is evident, but the origin of others will probably never be known. There is no reason why they should not have been invented by some priest or teacher or guild, by the order of some king, or as part of the mysticism of some temple. Whatever the origin, they were no better than scores of other ancient systems and no better than the present Chinese system when written without the zero, and there would never have been any chance of their triumphal progress westward had it not been for this relatively late symbol. There could hardly be demanded a stronger proof of the Hindu origin of the character for zero than this, and to it further reference will be made in Chapter IV.
LATER HINDU FORMS, WITH A PLACE VALUE
Before speaking of the perfected Hindu numerals with the zero and the place value, it is necessary to consider the third system mentioned on page 19,—the word and letter forms. The use of words with place value began at least as early as the 6th century of the Christian era. In many of the manuals of astronomy and mathematics, and often in other works in mentioning dates, numbers are represented by the names of certain objects or ideas. For example, zero is represented by "the void" (śūnya), or "heaven-space" (ambara ākāśa); one by "stick" (rupa), "moon" (indu śaśin), "earth" (bhū), "beginning" (ādi), "Brahma," or, in general, by anything markedly unique; two by "the twins" (yama), "hands" (kara), "eyes" (nayana), etc.; four by "oceans," five by "senses" (viṣaya) or "arrows" (the five arrows of Kāmadēva); six by "seasons" or "flavors"; seven by "mountain" (aga), and so on.[130] These names, accommodating themselves to the verse in which scientific works were written, had the additional advantage of not admitting, as did the figures, easy alteration, since any change would tend to disturb the meter.
As an example of this system, the date "Śaka Saṃvat, 867" (A.D. 945 or 946), is given by "giri-raṣa-vasu," meaning "the mountains" (seven), "the flavors" (six), and the gods "Vasu" of which there were eight. In reading the date these are read from right to left.[131] The period of invention of this system is uncertain. The first trace seems to be in the Śrautasūtra of Kātyāyana and Lāṭyāyana.[132] It was certainly known to Varāha-Mihira (d. 587),[133] for he used it in the Bṛhat-Saṃhitā.[134] It has also been asserted[135] that Āryabhaṭa (c. 500 A.D.) was familiar with this system, but there is nothing to prove the statement.[136] The earliest epigraphical examples of the system are found in the Bayang (Cambodia) inscriptions of 604 and 624 A.D.[137]
Mention should also be made, in this connection, of a curious system of alphabetic numerals that sprang up in southern India. In this we have the numerals represented by the letters as given in the following table:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| k | kh | g | gh | ṅ | c | ch | j | jh | ñ |
| ṭ | ṭh | ḍ | ḍh | ṇ | t | th | d | th | n |
| p | ph | b | bh | m | |||||
| y | r | l | v | ś | ṣ | s | h | l |
By this plan a numeral might be represented by any one of several letters, as shown in the preceding table, and thus it could the more easily be formed into a word for mnemonic purposes. For example, the word
| 2 | 3 | 1 | 5 | 6 | 5 | 1 |
| kha | gont | yan | me | ṣa | mā | pa |
has the value 1,565,132, reading from right to left.[138] This, the oldest specimen (1184 A.D.) known of this notation, is given in a commentary on the Rigveda, representing the number of days that had elapsed from the beginning of the Kaliyuga. Burnell[139] states that this system is even yet in use for remembering rules to calculate horoscopes, and for astronomical tables.
A second system of this kind is still used in the pagination of manuscripts in Ceylon, Siam, and Burma, having also had its rise in southern India. In this the thirty-four consonants when followed by a (as ka ... la) designate the numbers 1-34; by ā (as kā ... lā), those from 35 to 68; by i (ki ... li), those from 69 to 102, inclusive; and so on.[140]
As already stated, however, the Hindu system as thus far described was no improvement upon many others of the ancients, such as those used by the Greeks and the Hebrews. Having no zero, it was impracticable to designate the tens, hundreds, and other units of higher order by the same symbols used for the units from one to nine. In other words, there was no possibility of place value without some further improvement. So the Nānā Ghāt [41]symbols required the writing of "thousand seven twenty-four" about like T 7, tw, 4 in modern symbols, instead of 7024, in which the seven of the thousands, the two of the tens (concealed in the word twenty, being originally "twain of tens," the -ty signifying ten), and the four of the units are given as spoken and the order of the unit (tens, hundreds, etc.) is given by the place. To complete the system only the zero was needed; but it was probably eight centuries after the Nānā Ghāt inscriptions were cut, before this important symbol appeared; and not until a considerably later period did it become well known. Who it was to whom the invention is due, or where he lived, or even in what century, will probably always remain a mystery.[141] It is possible that one of the forms of ancient abacus suggested to some Hindu astronomer or mathematician the use of a symbol to stand for the vacant line when the counters were removed. It is well established that in different parts of India the names of the higher powers took different forms, even the order being interchanged.[142] Nevertheless, as the significance of the name of the unit was given by the order in reading, these variations did not lead to error. Indeed the variation itself may have necessitated the introduction of a word to signify a vacant place or lacking unit, with the ultimate introduction of a zero symbol for this word.
To enable us to appreciate the force of this argument a large number, 8,443,682,155, may be considered as the Hindus wrote and read it, and then, by way of contrast, as the Greeks and Arabs would have read it.
Modern American reading, 8 billion, 443 million, 682 thousand, 155.
Hindu, 8 padmas, 4 vyarbudas, 4 kōṭis, 3 prayutas, 6 lakṣas, 8 ayutas, 2 sahasra, 1 śata, 5 daśan, 5.
Arabic and early German, eight thousand thousand thousand and four hundred thousand thousand and forty-three thousand thousand, and six hundred thousand and eighty-two thousand and one hundred fifty-five (or five and fifty).
Greek, eighty-four myriads of myriads and four thousand three hundred sixty-eight myriads and two thousand and one hundred fifty-five.
As Woepcke[143] pointed out, the reading of numbers of this kind shows that the notation adopted by the Hindus tended to bring out the place idea. No other language than the Sanskrit has made such consistent application, in numeration, of the decimal system of numbers. The introduction of myriads as in the Greek, and thousands as in Arabic and in modern numeration, is really a step away from a decimal scheme. So in the numbers below one hundred, in English, eleven and twelve are out of harmony with the rest of the -teens, while the naming of all the numbers between ten and twenty is not analogous to the naming of the numbers above twenty. To conform to our written system we should have ten-one, ten-two, ten-three, and so on, as we have twenty-one, twenty-two, and the like. The Sanskrit is consistent, the units, however, preceding the tens and hundreds. Nor did any other ancient people carry the numeration as far as did the Hindus.[144]
When the aṅkapalli,[145] the decimal-place system of writing numbers, was perfected, the tenth symbol was called the śūnyabindu, generally shortened to śūnya (the void). Brockhaus[146] has well said that if there was any invention for which the Hindus, by all their philosophy and religion, were well fitted, it was the invention of a symbol for zero. This making of nothingness the crux of a tremendous achievement was a step in complete harmony with the genius of the Hindu.
It is generally thought that this śūnya as a symbol was not used before about 500 A.D., although some writers have placed it earlier.[147] Since Āryabhaṭa gives our common method of extracting roots, it would seem that he may have known a decimal notation,[148] although he did not use the characters from which our numerals are derived.[149] Moreover, he frequently speaks of the [44]void.[150] If he refers to a symbol this would put the zero as far back as 500 A.D., but of course he may have referred merely to the concept of nothingness.
A little later, but also in the sixth century, Varāha-Mihira[151] wrote a work entitled Bṛhat Saṃhitā[152] in which he frequently uses śūnya in speaking of numerals, so that it has been thought that he was referring to a definite symbol. This, of course, would add to the probability that Āryabhaṭa was doing the same.
It should also be mentioned as a matter of interest, and somewhat related to the question at issue, that Varāha-Mihira used the word-system with place value[153] as explained above.
The first kind of alphabetic numerals and also the word-system (in both of which the place value is used) are plays upon, or variations of, position arithmetic, which would be most likely to occur in the country of its origin.[154]
At the opening of the next century (c. 620 A.D.) Bāṇa[155] wrote of Subandhus's Vāsavadattā as a celebrated work, [45]and mentioned that the stars dotting the sky are here compared with zeros, these being points as in the modern Arabic system. On the other hand, a strong argument against any Hindu knowledge of the symbol zero at this time is the fact that about 700 A.D. the Arabs overran the province of Sind and thus had an opportunity of knowing the common methods used there for writing numbers. And yet, when they received the complete system in 776 they looked upon it as something new.[156] Such evidence is not conclusive, but it tends to show that the complete system was probably not in common use in India at the beginning of the eighth century. On the other hand, we must bear in mind the fact that a traveler in Germany in the year 1700 would probably have heard or seen nothing of decimal fractions, although these were perfected a century before that date. The élite of the mathematicians may have known the zero even in Āryabhaṭa's time, while the merchants and the common people may not have grasped the significance of the novelty until a long time after. On the whole, the evidence seems to point to the west coast of India as the region where the complete system was first seen.[157] As mentioned above, traces of the numeral words with place value, which do not, however, absolutely require a decimal place-system of symbols, are found very early in Cambodia, as well as in India.
Concerning the earliest epigraphical instances of the use of the nine symbols, plus the zero, with place value, there [46]is some question. Colebrooke[158] in 1807 warned against the possibility of forgery in many of the ancient copper-plate land grants. On this account Fleet, in the Indian Antiquary,[159] discusses at length this phase of the work of the epigraphists in India, holding that many of these forgeries were made about the end of the eleventh century. Colebrooke[160] takes a more rational view of these forgeries than does Kaye, who seems to hold that they tend to invalidate the whole Indian hypothesis. "But even where that may be suspected, the historical uses of a monument fabricated so much nearer to the times to which it assumes to belong, will not be entirely superseded. The necessity of rendering the forged grant credible would compel a fabricator to adhere to history, and conform to established notions: and the tradition, which prevailed in his time, and by which he must be guided, would probably be so much nearer to the truth, as it was less remote from the period which it concerned."[161] Bühler[162] gives the copper-plate Gurjara inscription of Cedi-saṃvat 346 (595 A.D.) as the oldest epigraphical use of the numerals[163] "in which the symbols correspond to the alphabet numerals of the period and the place." Vincent A. Smith[164] quotes a stone inscription of 815 A.D., dated Saṃvat 872. So F. Kielhorn in the Epigraphia Indica[165] gives a Pathari pillar inscription of Parabala, dated Vikrama-saṃvat 917, which corresponds to 861 A.D., [47]and refers also to another copper-plate inscription dated Vikrama-saṃvat 813 (756 A.D.). The inscription quoted by V. A. Smith above is that given by D. R. Bhandarkar,[166] and another is given by the same writer as of date Saka-saṃvat 715 (798 A.D.), being incised on a pilaster. Kielhorn[167] also gives two copper-plate inscriptions of the time of Mahendrapala of Kanauj, Valhabī-saṃvat 574 (893 A.D.) and Vikrama-saṃvat 956 (899 A.D.). That there should be any inscriptions of date as early even as 750 A.D., would tend to show that the system was at least a century older. As will be shown in the further development, it was more than two centuries after the introduction of the numerals into Europe that they appeared there upon coins and inscriptions. While Thibaut[168] does not consider it necessary to quote any specific instances of the use of the numerals, he states that traces are found from 590 A.D. on. "That the system now in use by all civilized nations is of Hindu origin cannot be doubted; no other nation has any claim upon its discovery, especially since the references to the origin of the system which are found in the nations of western Asia point unanimously towards India."[169]
The testimony and opinions of men like Bühler, Kielhorn, V. A. Smith, Bhandarkar, and Thibaut are entitled to the most serious consideration. As authorities on ancient Indian epigraphy no others rank higher. Their work is accepted by Indian scholars the world over, and their united judgment as to the rise of the system with a place value—that it took place in India as early as the [48]sixth century A.D.—must stand unless new evidence of great weight can be submitted to the contrary.
Many early writers remarked upon the diversity of Indian numeral forms. Al-Bīrūnī was probably the first; noteworthy is also Johannes Hispalensis,[170] who gives the variant forms for seven and four. We insert on p. 49 a table of numerals used with place value. While the chief authority for this is Bühler,[171] several specimens are given which are not found in his work and which are of unusual interest.
The Śāradā forms given in the table use the circle as a symbol for 1 and the dot for zero. They are taken from the paging and text of The Kashmirian Atharva-Veda[172], of which the manuscript used is certainly four hundred years old. Similar forms are found in a manuscript belonging to the University of Tübingen. Two other series presented are from Tibetan books in the library of one of the authors.
For purposes of comparison the modern Sanskrit and Arabic numeral forms are added.
| Sanskrit, | 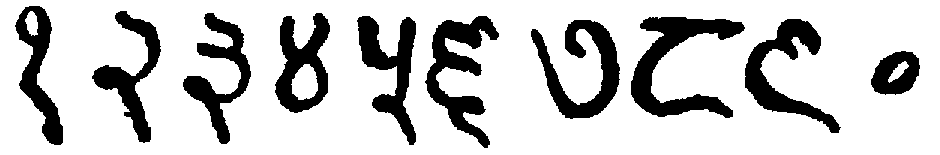 |
| Arabic, | 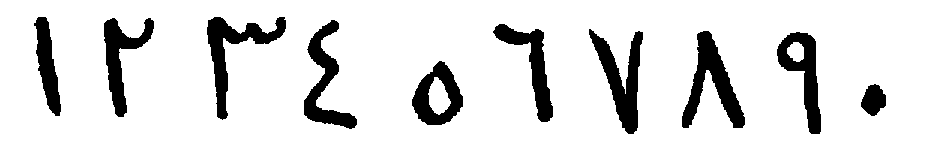 |
 | |
| a [173] | 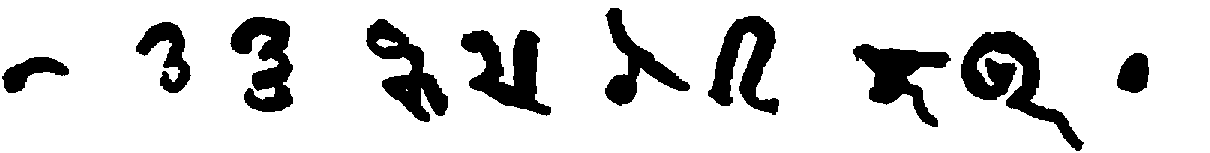 |
| b [174] | 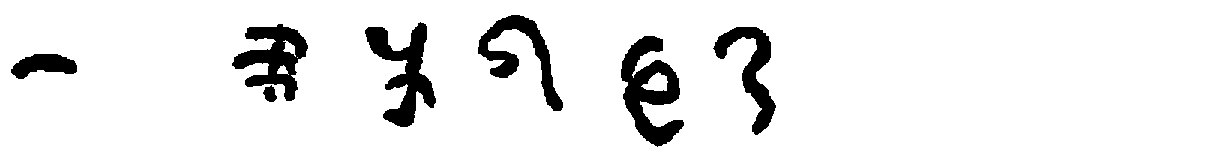 |
| c [175] |  |
| d [176] | 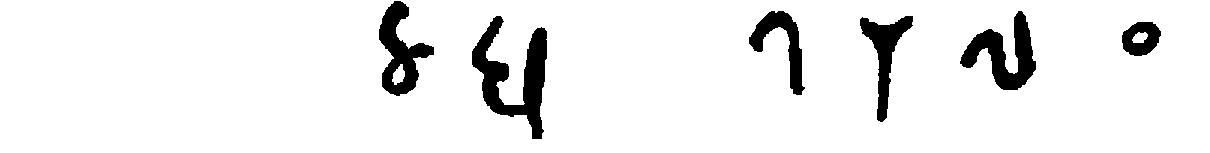 |
| e [177] | 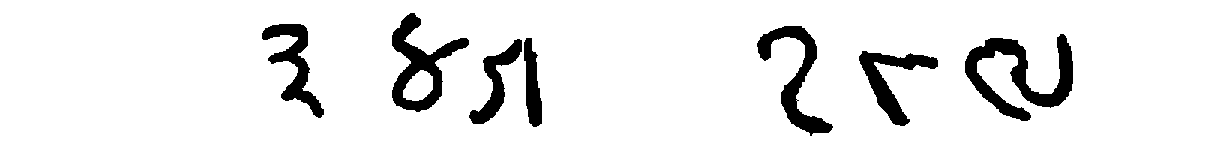 |
| f [178] | 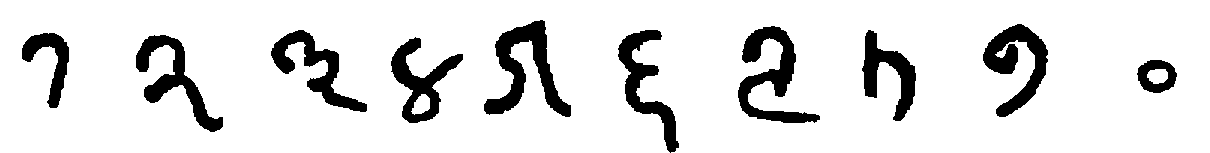 |
| g [179] | 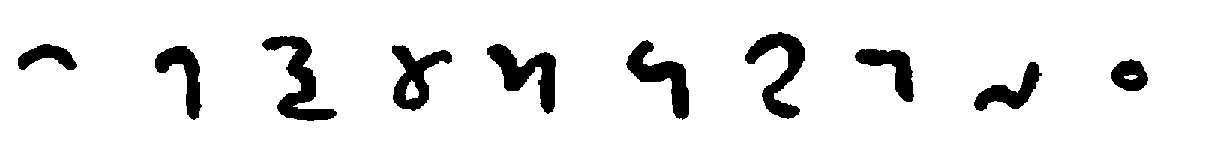 |
| h [180] | 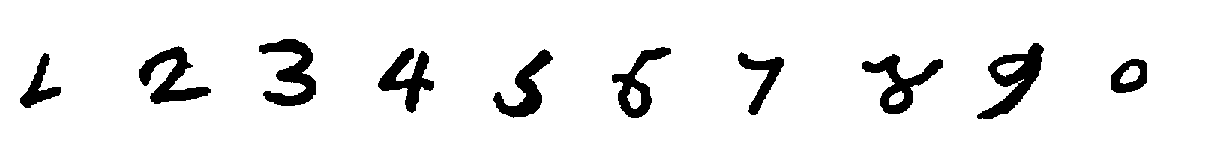 |
| i [180] | 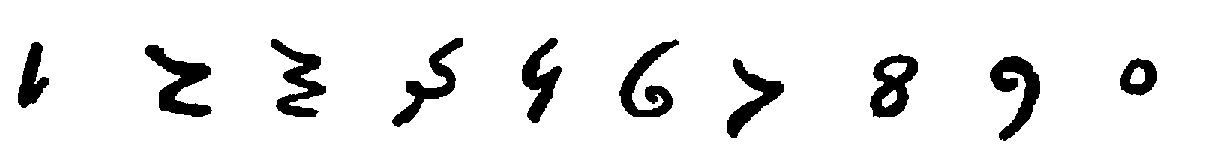 |
| j [181] | 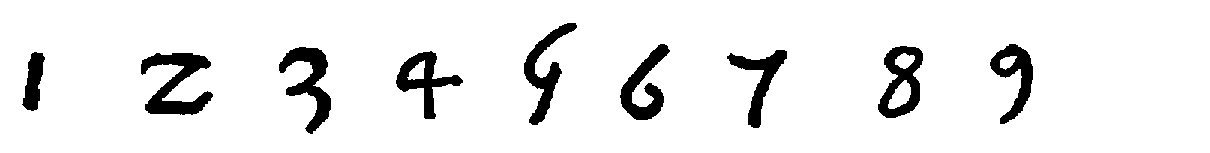 |
| k [181] | 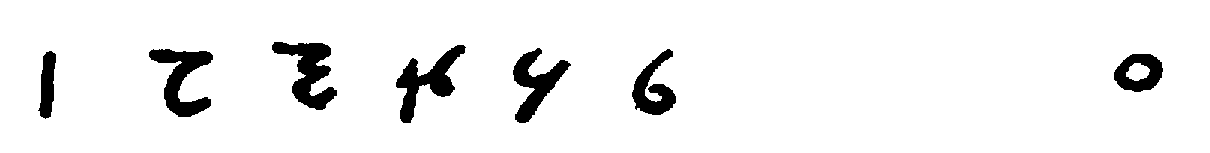 |
| l [182] | 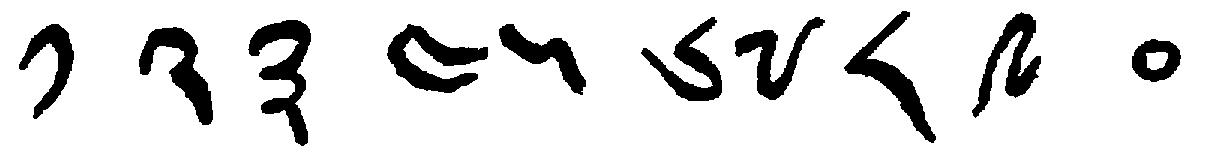 |
| m [183] |  |
| n [184] | 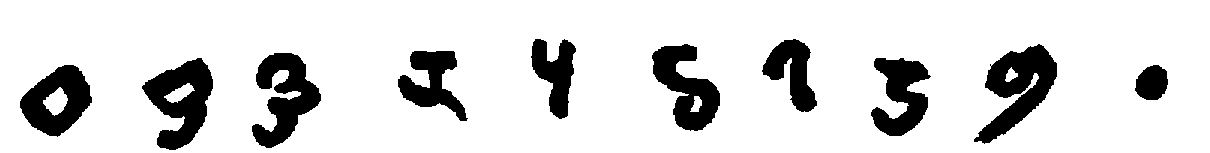 |
THE SYMBOL ZERO
What has been said of the improved Hindu system with a place value does not touch directly the origin of a symbol for zero, although it assumes that such a symbol exists. The importance of such a sign, the fact that it is a prerequisite to a place-value system, and the further fact that without it the Hindu-Arabic numerals would never have dominated the computation system of the western world, make it proper to devote a chapter to its origin and history.
It was some centuries after the primitive Brāhmī and Kharoṣṭhī
numerals had made their appearance in India that the zero first appeared
there, although such a character was used by the Babylonians[185] in the centuries
immediately preceding the Christian era. The symbol is 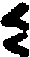 or
or  , and apparently it
was not used in calculation. Nor does it always occur when units of any
order are lacking; thus 180 is written
, and apparently it
was not used in calculation. Nor does it always occur when units of any
order are lacking; thus 180 is written 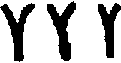 with the meaning three sixties and no units, since
181 immediately following is
with the meaning three sixties and no units, since
181 immediately following is  , three sixties and one unit.[186] The main [52]use of this Babylonian
symbol seems to have been in the fractions, 60ths, 3600ths, etc., and
somewhat similar to the Greek use of ο, for οὐδέν, with the meaning
vacant.
, three sixties and one unit.[186] The main [52]use of this Babylonian
symbol seems to have been in the fractions, 60ths, 3600ths, etc., and
somewhat similar to the Greek use of ο, for οὐδέν, with the meaning
vacant.
"The earliest undoubted occurrence of a zero in India is an
inscription at Gwalior, dated Samvat 933 (876 A.D.). Where 50 garlands are mentioned (line 20), 50
is written 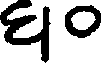 . 270
(line 4) is written
. 270
(line 4) is written 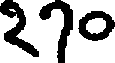 ."[187] The Bakhṣālī
Manuscript[188] probably
antedates this, using the point or dot as a zero symbol. Bayley mentions
a grant of Jaika Rashtrakúta of Bharuj, found at Okamandel, of date 738
A.D., which contains a zero, and also a coin
with indistinct Gupta date 707 (897 A.D.), but
the reliability of Bayley's work is questioned. As has been noted, the
appearance of the numerals in inscriptions and on coins would be of much
later occurrence than the origin and written exposition of the system.
From the period mentioned the spread was rapid over all of India, save
the southern part, where the Tamil and Malayalam people retain the old
system even to the present day.[189]
."[187] The Bakhṣālī
Manuscript[188] probably
antedates this, using the point or dot as a zero symbol. Bayley mentions
a grant of Jaika Rashtrakúta of Bharuj, found at Okamandel, of date 738
A.D., which contains a zero, and also a coin
with indistinct Gupta date 707 (897 A.D.), but
the reliability of Bayley's work is questioned. As has been noted, the
appearance of the numerals in inscriptions and on coins would be of much
later occurrence than the origin and written exposition of the system.
From the period mentioned the spread was rapid over all of India, save
the southern part, where the Tamil and Malayalam people retain the old
system even to the present day.[189]
Aside from its appearance in early inscriptions, there is still another indication of the Hindu origin of the symbol in the special treatment of the concept zero in the early works on arithmetic. Brahmagupta, who lived in Ujjain, the center of Indian astronomy,[190] in the early part [53]of the seventh century, gives in his arithmetic[191] a distinct treatment of the properties of zero. He does not discuss a symbol, but he shows by his treatment that in some way zero had acquired a special significance not found in the Greek or other ancient arithmetics. A still more scientific treatment is given by Bhāskara,[192] although in one place he permits himself an unallowed liberty in dividing by zero. The most recently discovered work of ancient Indian mathematical lore, the Ganita-Sāra-Saṅgraha[193] of Mahāvīrācārya (c. 830 A.D.), while it does not use the numerals with place value, has a similar discussion of the calculation with zero.
What suggested the form for the zero is, of course, purely a matter of conjecture. The dot, which the Hindus used to fill up lacunæ in their manuscripts, much as we indicate a break in a sentence,[194] would have been a more natural symbol; and this is the one which the Hindus first used[195] and which most Arabs use to-day. There was also used for this purpose a cross, like our X, and this is occasionally found as a zero symbol.[196] In the Bakhṣālī manuscript above mentioned, the word śūnya, with the dot as its symbol, is used to denote the unknown quantity, as well as to denote zero. An analogous use of the [54]zero, for the unknown quantity in a proportion, appears in a Latin manuscript of some lectures by Gottfried Wolack in the University of Erfurt in 1467 and 1468.[197] The usage was noted even as early as the eighteenth century.[198]
The small circle was possibly suggested by the spurred circle which
was used for ten.[199] It
has also been thought that the omicron used by Ptolemy in his
Almagest, to mark accidental blanks in the sexagesimal system
which he employed, may have influenced the Indian writers.[200] This symbol was used
quite generally in Europe and Asia, and the Arabic astronomer
Al-Battānī[201] (died 929 A.D.) used a similar symbol in connection with the
alphabetic system of numerals. The occasional use by
Al-Battānī of the Arabic negative, lā, to
indicate the absence of minutes [55](or seconds), is noted by Nallino.[202] Noteworthy is also the
use of the  for unity in the
Śāradā characters of the Kashmirian Atharva-Veda, the
writing being at least 400 years old. Bhāskara (c. 1150) used a
small circle above a number to indicate subtraction, and in the Tartar
writing a redundant word is removed by drawing an oval around it. It
would be interesting to know whether our score mark
for unity in the
Śāradā characters of the Kashmirian Atharva-Veda, the
writing being at least 400 years old. Bhāskara (c. 1150) used a
small circle above a number to indicate subtraction, and in the Tartar
writing a redundant word is removed by drawing an oval around it. It
would be interesting to know whether our score mark 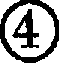 , read "four in the hole,"
could trace its pedigree to the same sources. O'Creat[203] (c. 1130), in a letter to his
teacher, Adelhard of Bath, uses τ
for zero, being an abbreviation for the word teca which we shall
see was one of the names used for zero, although it could quite as well
be from τζίφρα. More rarely O'Creat uses
, read "four in the hole,"
could trace its pedigree to the same sources. O'Creat[203] (c. 1130), in a letter to his
teacher, Adelhard of Bath, uses τ
for zero, being an abbreviation for the word teca which we shall
see was one of the names used for zero, although it could quite as well
be from τζίφρα. More rarely O'Creat uses  , applying the name
cyfra to both forms. Frater Sigsboto[204] (c. 1150) uses the same symbol. Other
peculiar forms are noted by Heiberg[205] as being in use among the Byzantine
Greeks in the fifteenth century. It is evident from the text that some of
these writers did not understand the import of the new system.[206]
, applying the name
cyfra to both forms. Frater Sigsboto[204] (c. 1150) uses the same symbol. Other
peculiar forms are noted by Heiberg[205] as being in use among the Byzantine
Greeks in the fifteenth century. It is evident from the text that some of
these writers did not understand the import of the new system.[206]
Although the dot was used at first in India, as noted above, the small
circle later replaced it and continues in use to this day. The Arabs,
however, did not adopt the [56]circle, since it bore some resemblance to
the letter which expressed the number five in the alphabet system.[207] The earliest Arabic
zero known is the dot, used in a manuscript of 873 A.D.[208] Sometimes both the dot and the circle
are used in the same work, having the same meaning, which is the case in
an Arabic MS., an abridged arithmetic of Jamshid,[209] 982 A.H. (1575 A.D.). As given in this work the numerals are  . The form for 5 varies, in some
works becoming
. The form for 5 varies, in some
works becoming 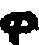 or
or 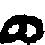 ;
; 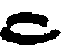 is found in Egypt and
is found in Egypt and 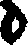 appears in some fonts of type. To-day the Arabs use the 0 only
when, under European influence, they adopt the ordinary system. Among the
Chinese the first definite trace of zero is in the work of Tsin[210] of 1247 A.D. The form is the circular one of the Hindus, and
undoubtedly was brought to China by some traveler.
appears in some fonts of type. To-day the Arabs use the 0 only
when, under European influence, they adopt the ordinary system. Among the
Chinese the first definite trace of zero is in the work of Tsin[210] of 1247 A.D. The form is the circular one of the Hindus, and
undoubtedly was brought to China by some traveler.
The name of this all-important symbol also demands some attention, especially as we are even yet quite undecided as to what to call it. We speak of it to-day as zero, naught, and even cipher; the telephone operator often calls it O, and the illiterate or careless person calls it aught. In view of all this uncertainty we may well inquire what it has been called in the past.[211]
As already stated, the Hindus called it śūnya, "void."[212] This passed over into the Arabic as aṣ-ṣifr or ṣifr.[213] When Leonard of Pisa (1202) wrote upon the Hindu numerals he spoke of this character as zephirum.[214] Maximus Planudes (1330), writing under both the Greek and the Arabic influence, called it tziphra.[215] In a treatise on arithmetic written in the Italian language by Jacob of Florence[216] [58](1307) it is called zeuero,[217] while in an arithmetic of Giovanni di Danti of Arezzo (1370) the word appears as çeuero.[218] Another form is zepiro,[219] which was also a step from zephirum to zero.[220]
Of course the English cipher, French chiffre, is derived from the same Arabic word, aṣ-ṣifr, but in several languages it has come to mean the numeral figures in general. A trace of this appears in our word ciphering, meaning figuring or computing.[221] Johann Huswirt[222] uses the word with both meanings; he gives for the tenth character the four names theca, circulus, cifra, and figura nihili. In this statement Huswirt probably follows, as did many writers of that period, the Algorismus of Johannes de Sacrobosco (c. 1250 A.D.), who was also known as John of Halifax or John of Holywood. The commentary of [59]Petrus de Dacia[223] (c. 1291 A.D.) on the Algorismus vulgaris of Sacrobosco was also widely used. The widespread use of this Englishman's work on arithmetic in the universities of that time is attested by the large number[224] of MSS. from the thirteenth to the seventeenth century still extant, twenty in Munich, twelve in Vienna, thirteen in Erfurt, several in England given by Halliwell,[225] ten listed in Coxe's Catalogue of the Oxford College Library, one in the Plimpton collection,[226] one in the Columbia University Library, and, of course, many others.
From aṣ-ṣifr has come zephyr, cipher, and finally the abridged form zero. The earliest printed work in which is found this final form appears to be Calandri's arithmetic of 1491,[227] while in manuscript it appears at least as early as the middle of the fourteenth century.[228] It also appears in a work, Le Kadran des marchans, by Jehan [60]Certain,[229] written in 1485. This word soon became fairly well known in Spain[230] and France.[231] The medieval writers also spoke of it as the sipos,[232] and occasionally as the wheel,[233] circulus[234] (in German das Ringlein[235]), circular [61]note,[236] theca,[237] long supposed to be from its resemblance to the Greek theta, but explained by Petrus de Dacia as being derived from the name of the iron[238] used to brand thieves and robbers with a circular mark placed on the forehead or on the cheek. It was also called omicron[239] (the Greek o), being sometimes written õ or φ to distinguish it from the letter o. It also went by the name null[240] (in the Latin books [62]nihil[241] or nulla,[242] and in the French rien[243]), and very commonly by the name cipher.[244] Wallis[245] gives one of the earliest extended discussions of the various forms of the word, giving certain other variations worthy of note, as ziphra, zifera, siphra, ciphra, tsiphra, tziphra, and the Greek τζίφρα.[246]
THE QUESTION OF THE INTRODUCTION OF THE NUMERALS INTO EUROPE BY BOETHIUS
Just as we were quite uncertain as to the origin of the numeral forms, so too are we uncertain as to the time and place of their introduction into Europe. There are two general theories as to this introduction. The first is that they were carried by the Moors to Spain in the eighth or ninth century, and thence were transmitted to Christian Europe, a theory which will be considered later. The second, advanced by Woepcke,[247] is that they were not brought to Spain by the Moors, but that they were already in Spain when the Arabs arrived there, having reached the West through the Neo-Pythagoreans. There are two facts to support this second theory: (1) the forms of these numerals are characteristic, differing materially from those which were brought by Leonardo of Pisa from Northern Africa early in the thirteenth century (before 1202 A.D.); (2) they are essentially those which [64]tradition has so persistently assigned to Boethius (c. 500 A.D.), and which he would naturally have received, if at all, from these same Neo-Pythagoreans or from the sources from which they derived them. Furthermore, Woepcke points out that the Arabs on entering Spain (711 A.D.) would naturally have followed their custom of adopting for the computation of taxes the numerical systems of the countries they conquered,[248] so that the numerals brought from Spain to Italy, not having undergone the same modifications as those of the Eastern Arab empire, would have differed, as they certainly did, from those that came through Bagdad. The theory is that the Hindu system, without the zero, early reached Alexandria (say 450 A.D.), and that the Neo-Pythagorean love for the mysterious and especially for the Oriental led to its use as something bizarre and cabalistic; that it was then passed along the Mediterranean, reaching Boethius in Athens or in Rome, and to the schools of Spain, being discovered in Africa and Spain by the Arabs even before they themselves knew the improved system with the place value.
A recent theory set forth by Bubnov[249] also deserves mention, chiefly because of the seriousness of purpose shown by this well-known writer. Bubnov holds that the forms first found in Europe are derived from ancient symbols used on the abacus, but that the zero is of Hindu origin. This theory does not seem tenable, however, in the light of the evidence already set forth.
Two questions are presented by Woepcke's theory: (1) What was the nature of these Spanish numerals, and how were they made known to Italy? (2) Did Boethius know them?
The Spanish forms of the numerals were called the ḥurūf al-ġobār, the ġobār or dust numerals, as distinguished from the ḥurūf al-jumal or alphabetic numerals. Probably the latter, under the influence of the Syrians or Jews,[250] were also used by the Arabs. The significance of the term ġobār is doubtless that these numerals were written on the dust abacus, this plan being distinct from the counter method of representing numbers. It is also worthy of note that Al-Bīrūnī states that the Hindus often performed numerical computations in the sand. The term is found as early as c. 950, in the verses of an anonymous writer of Kairwān, in Tunis, in which the author speaks of one of his works on ġobār calculation;[251] and, much later, the Arab writer Abū Bekr Moḥammed ibn ‛Abdallāh, surnamed al-Ḥaṣṣār [66](the arithmetician), wrote a work of which the second chapter was "On the dust figures."[252]
The ġobār numerals themselves were first made known to
modern scholars by Silvestre de Sacy, who discovered them in an Arabic
manuscript from the library of the ancient abbey of
St.-Germain-des-Prés.[253] The system has nine characters, but
no zero. A dot above a character indicates tens, two dots hundreds, and
so on, 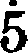 meaning 50, and
meaning 50, and
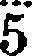 meaning 5000. It has been
suggested that possibly these dots, sprinkled like dust above the
numerals, gave rise to the word ġobār,[254] but this is not at all
probable. This system of dots is found in Persia at a much later date
with numerals quite like the modern Arabic;[255] but that it was used at all is
significant, for it is hardly likely that the western system would go
back to Persia, when the perfected Hindu one was near at hand.
meaning 5000. It has been
suggested that possibly these dots, sprinkled like dust above the
numerals, gave rise to the word ġobār,[254] but this is not at all
probable. This system of dots is found in Persia at a much later date
with numerals quite like the modern Arabic;[255] but that it was used at all is
significant, for it is hardly likely that the western system would go
back to Persia, when the perfected Hindu one was near at hand.
At first sight there would seem to be some reason for believing that this feature of the ġobār system was of [67]Arabic origin, and that the present zero of these people,[256] the dot, was derived from it. It was entirely natural that the Semitic people generally should have adopted such a scheme, since their diacritical marks would suggest it, not to speak of the possible influence of the Greek accents in the Hellenic number system. When we consider, however, that the dot is found for zero in the Bakhṣālī manuscript,[257] and that it was used in subscript form in the Kitāb al-Fihrist[258] in the tenth century, and as late as the sixteenth century,[259] although in this case probably under Arabic influence, we are forced to believe that this form may also have been of Hindu origin.
The fact seems to be that, as already stated,[260] the Arabs did not immediately adopt the Hindu zero, because it resembled their 5; they used the superscript dot as serving their purposes fairly well; they may, indeed, have carried this to the west and have added it to the ġobār forms already there, just as they transmitted it to the Persians. Furthermore, the Arab and Hebrew scholars of Northern Africa in the tenth century knew these numerals as Indian forms, for a commentary on the Sēfer Yeṣīrāh by Abū Sahl ibn Tamim (probably composed at Kairwān, c. 950) speaks of "the Indian arithmetic known under the name of ġobār or dust calculation."[261] All this suggests that the Arabs may very [68]likely have known the ġobār forms before the numerals reached them again in 773.[262] The term "ġobār numerals" was also used without any reference to the peculiar use of dots.[263] In this connection it is worthy of mention that the Algerians employed two different forms of numerals in manuscripts even of the fourteenth century,[264] and that the Moroccans of to-day employ the European forms instead of the present Arabic.
The Indian use of subscript dots to indicate the tens, hundreds, thousands, etc., is established by a passage in the Kitāb al-Fihrist[265] (987 A.D.) in which the writer discusses the written language of the people of India. Notwithstanding the importance of this reference for the early history of the numerals, it has not been mentioned by previous writers on this subject. The numeral forms given are those which have usually been called Indian,[266] in opposition to ġobār. In this document the dots are placed below the characters, instead of being superposed as described above. The significance was the same.
In form these ġobār numerals resemble our own much more closely than the Arab numerals do. They varied more or less, but were substantially as follows:
| 1 [267] | 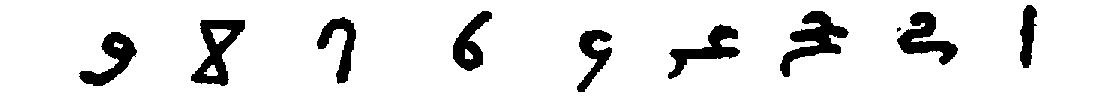 |
| 2 [268] | 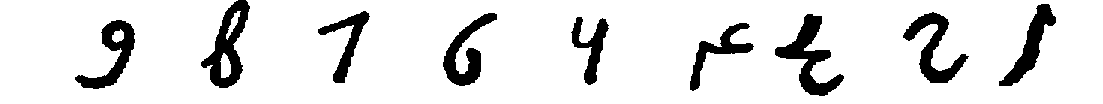 |
| 3 [269] | 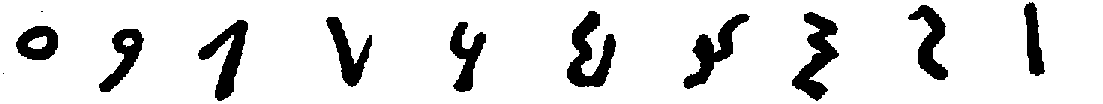 |
| 4 [270] |  |
| 5 [271] |  |
| 6 [271] | 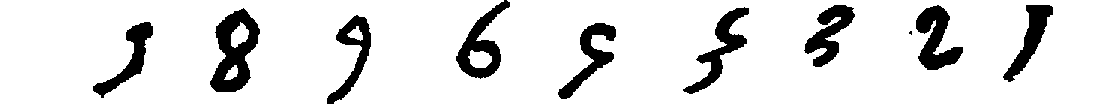 |
The question of the possible influence of the Egyptian demotic and hieratic ordinal forms has been so often suggested that it seems well to introduce them at this point, for comparison with the ġobār forms. They would as appropriately be used in connection with the Hindu forms, and the evidence of a relation of the first three with all these systems is apparent. The only further resemblance is in the Demotic 4 and in the 9, so that the statement that the Hindu forms in general came from [70]this source has no foundation. The first four Egyptian cardinal numerals[272] resemble more the modern Arabic.
This theory of the very early introduction of the numerals into Europe
fails in several points. In the first place the early Western forms are
not known; in the second place some early Eastern forms are like the
ġobār, as is seen in the third line on p. 69, where the forms are from a manuscript written at
Shiraz about 970 A.D., and in which some
western Arabic forms, e.g.  for 2, are also used. Probably most significant of all is the fact
that the ġobār numerals as given by Sacy are all, with the
exception of the symbol for eight, either single Arabic letters or
combinations of letters. So much for the Woepcke theory and the meaning
of the ġobār numerals. We now have to consider the question
as to whether Boethius knew these ġobār forms, or forms akin
to them.
for 2, are also used. Probably most significant of all is the fact
that the ġobār numerals as given by Sacy are all, with the
exception of the symbol for eight, either single Arabic letters or
combinations of letters. So much for the Woepcke theory and the meaning
of the ġobār numerals. We now have to consider the question
as to whether Boethius knew these ġobār forms, or forms akin
to them.
This large question[273] suggests several minor ones: (1) Who was Boethius? (2) Could he have known these numerals? (3) Is there any positive or strong circumstantial evidence that he did know them? (4) What are the probabilities in the case?
First, who was Boethius,—Divus[274] Boethius as he was called in the Middle Ages? Anicius Manlius Severinus Boethius[275] was born at Rome c. 475. He was a member of the distinguished family of the Anicii,[276] which had for some time before his birth been Christian. Early left an orphan, the tradition is that he was taken to Athens at about the age of ten, and that he remained there eighteen years.[277] He married Rusticiana, daughter of the senator Symmachus, and this union of two such powerful families allowed him to move in the highest circles.[278] Standing strictly for the right, and against all iniquity at court, he became the object of hatred on the part of all the unscrupulous element near the throne, and his bold defense of the ex-consul Albinus, unjustly accused of treason, led to his imprisonment at Pavia[279] and his execution in 524.[280] Not many generations after his death, the period being one in which historical criticism was at its lowest ebb, the church found it profitable to look upon his execution as a martyrdom.[281] He was [72]accordingly looked upon as a saint,[282] his bones were enshrined,[283] and as a natural consequence his books were among the classics in the church schools for a thousand years.[284] It is pathetic, however, to think of the medieval student trying to extract mental nourishment from a work so abstract, so meaningless, so unnecessarily complicated, as the arithmetic of Boethius.
He was looked upon by his contemporaries and immediate successors as a master, for Cassiodorus[285] (c. 490-c. 585 A.D.) says to him: "Through your translations the music of Pythagoras and the astronomy of Ptolemy are read by those of Italy, and the arithmetic of Nicomachus and the geometry of Euclid are known to those of the West."[286] Founder of the medieval scholasticism, [73]distinguishing the trivium and quadrivium,[287] writing the only classics of his time, Gibbon well called him "the last of the Romans whom Cato or Tully could have acknowledged for their countryman."[288]
The second question relating to Boethius is this: Could he possibly have known the Hindu numerals? In view of the relations that will be shown to have existed between the East and the West, there can only be an affirmative answer to this question. The numerals had existed, without the zero, for several centuries; they had been well known in India; there had been a continued interchange of thought between the East and West; and warriors, ambassadors, scholars, and the restless trader, all had gone back and forth, by land or more frequently by sea, between the Mediterranean lands and the centers of Indian commerce and culture. Boethius could very well have learned one or more forms of Hindu numerals from some traveler or merchant.
To justify this statement it is necessary to speak more fully of these relations between the Far East and Europe. It is true that we have no records of the interchange of learning, in any large way, between eastern Asia and central Europe in the century preceding the time of Boethius. But it is one of the mistakes of scholars to believe that they are the sole transmitters of knowledge. [74]As a matter of fact there is abundant reason for believing that Hindu numerals would naturally have been known to the Arabs, and even along every trade route to the remote west, long before the zero entered to make their place-value possible, and that the characters, the methods of calculating, the improvements that took place from time to time, the zero when it appeared, and the customs as to solving business problems, would all have been made known from generation to generation along these same trade routes from the Orient to the Occident. It must always be kept in mind that it was to the tradesman and the wandering scholar that the spread of such learning was due, rather than to the school man. Indeed, Avicenna[289] (980-1037 A.D.) in a short biography of himself relates that when his people were living at Bokhāra his father sent him to the house of a grocer to learn the Hindu art of reckoning, in which this grocer (oil dealer, possibly) was expert. Leonardo of Pisa, too, had a similar training.
The whole question of this spread of mercantile knowledge along the trade routes is so connected with the ġobār numerals, the Boethius question, Gerbert, Leonardo of Pisa, and other names and events, that a digression for its consideration now becomes necessary.[290]
Even in very remote times, before the Hindu numerals were sculptured in the cave of Nānā Ghāt, there were trade relations between Arabia and India. Indeed, long before the Aryans went to India the great Turanian race had spread its civilization from the Mediterranean to the Indus.[291] At a much later period the Arabs were the intermediaries between Egypt and Syria on the west, and the farther Orient.[292] In the sixth century B.C., Hecatæus,[293] the father of geography, was acquainted not only with the Mediterranean lands but with the countries as far as the Indus,[294] and in Biblical times there were regular triennial voyages to India. Indeed, the story of Joseph bears witness to the caravan trade from India, across Arabia, and on to the banks of the Nile. About the same time as Hecatæus, Scylax, a Persian admiral under Darius, from Caryanda on the coast of Asia Minor, traveled to [76]northwest India and wrote upon his ventures.[295] He induced the nations along the Indus to acknowledge the Persian supremacy, and such number systems as there were in these lands would naturally have been known to a man of his attainments.
A century after Scylax, Herodotus showed considerable knowledge of India, speaking of its cotton and its gold,[296] telling how Sesostris[297] fitted out ships to sail to that country, and mentioning the routes to the east. These routes were generally by the Red Sea, and had been followed by the Phœnicians and the Sabæans, and later were taken by the Greeks and Romans.[298]
In the fourth century B.C. the West and East came into very close relations. As early as 330, Pytheas of Massilia (Marseilles) had explored as far north as the northern end of the British Isles and the coasts of the German Sea, while Macedon, in close touch with southern France, was also sending her armies under Alexander[299] through Afghanistan as far east as the Punjab.[300] Pliny tells us that Alexander the Great employed surveyors to measure [77]the roads of India; and one of the great highways is described by Megasthenes, who in 295 B.C., as the ambassador of Seleucus, resided at Pātalīpuṭra, the present Patna.[301]
The Hindus also learned the art of coining from the Greeks, or possibly from the Chinese, and the stores of Greco-Hindu coins still found in northern India are a constant source of historical information.[302] The Rāmāyana speaks of merchants traveling in great caravans and embarking by sea for foreign lands.[303] Ceylon traded with Malacca and Siam, and Java was colonized by Hindu traders, so that mercantile knowledge was being spread about the Indies during all the formative period of the numerals.
Moreover the results of the early Greek invasion were embodied by Dicæarchus of Messana (about 320 B.C.) in a map that long remained a standard. Furthermore, Alexander did not allow his influence on the East to cease. He divided India into three satrapies,[304] placing Greek governors over two of them and leaving a Hindu ruler in charge of the third, and in Bactriana, a part of Ariana or ancient Persia, he left governors; and in these the western civilization was long in evidence. Some of the Greek and Roman metrical and astronomical terms [78]found their way, doubtless at this time, into the Sanskrit language.[305] Even as late as from the second to the fifth centuries A.D., Indian coins showed the Hellenic influence. The Hindu astronomical terminology reveals the same relationship to western thought, for Varāha-Mihira (6th century A.D.), a contemporary of Āryabhaṭa, entitled a work of his the Bṛhat-Saṃhitā, a literal translation of μεγάλη σύνταξις of Ptolemy;[306] and in various ways is this interchange of ideas apparent.[307] It could not have been at all unusual for the ancient Greeks to go to India, for Strabo lays down the route, saying that all who make the journey start from Ephesus and traverse Phrygia and Cappadocia before taking the direct road.[308] The products of the East were always finding their way to the West, the Greeks getting their ginger[309] from Malabar, as the Phœnicians had long before brought gold from Malacca.
Greece must also have had early relations with China, for there is a notable similarity between the Greek and Chinese life, as is shown in their houses, their domestic customs, their marriage ceremonies, the public story-tellers, the puppet shows which Herodotus says were introduced from Egypt, the street jugglers, the games of dice,[310] the game of finger-guessing,[311] the water clock, the [79]music system, the use of the myriad,[312] the calendars, and in many other ways.[313] In passing through the suburbs of Peking to-day, on the way to the Great Bell temple, one is constantly reminded of the semi-Greek architecture of Pompeii, so closely does modern China touch the old classical civilization of the Mediterranean. The Chinese historians tell us that about 200 B.C. their arms were successful in the far west, and that in 180 B.C. an ambassador went to Bactria, then a Greek city, and reported that Chinese products were on sale in the markets there.[314] There is also a noteworthy resemblance between certain Greek and Chinese words,[315] showing that in remote times there must have been more or less interchange of thought.
The Romans also exchanged products with the East. Horace says, "A busy trader, you hasten to the farthest Indies, flying from poverty over sea, over crags, over fires."[316] The products of the Orient, spices and jewels from India, frankincense from Persia, and silks from China, being more in demand than the exports from the Mediterranean lands, the balance of trade was against the West, and thus Roman coin found its way eastward. In 1898, for example, a number of Roman coins dating from 114 B.C. to Hadrian's time were found at Paklī, a part of the Hazāra district, sixteen miles north of Abbottābād,[317] and numerous similar discoveries have been made from time to time.
Augustus speaks of envoys received by him from India, a thing never before known,[318] and it is not improbable that he also received an embassy from China.[319] Suetonius (first century A.D.) speaks in his history of these relations,[320] as do several of his contemporaries,[321] and Vergil[322] tells of Augustus doing battle in Persia. In Pliny's time the trade of the Roman Empire with Asia amounted to a million and a quarter dollars a year, a sum far greater relatively then than now,[323] while by the time of Constantine Europe was in direct communication with the Far East.[324]
In view of these relations it is not beyond the range of possibility that proof may sometime come to light to show that the Greeks and Romans knew something of the [81]number system of India, as several writers have maintained.[325]
Returning to the East, there are many evidences of the spread of knowledge in and about India itself. In the third century B.C. Buddhism began to be a connecting medium of thought. It had already permeated the Himalaya territory, had reached eastern Turkestan, and had probably gone thence to China. Some centuries later (in 62 A.D.) the Chinese emperor sent an ambassador to India, and in 67 A.D. a Buddhist monk was invited to China.[326] Then, too, in India itself Aśoka, whose name has already been mentioned in this work, extended the boundaries of his domains even into Afghanistan, so that it was entirely possible for the numerals of the Punjab to have worked their way north even at that early date.[327]
Furthermore, the influence of Persia must not be forgotten in considering this transmission of knowledge. In the fifth century the Persian medical school at Jondi-Sapur admitted both the Hindu and the Greek doctrines, and Firdusī tells us that during the brilliant reign of [82]Khosrū I,[328] the golden age of Pahlavī literature, the Hindu game of chess was introduced into Persia, at a time when wars with the Greeks were bringing prestige to the Sassanid dynasty.
Again, not far from the time of Boethius, in the sixth century, the Egyptian monk Cosmas, in his earlier years as a trader, made journeys to Abyssinia and even to India and Ceylon, receiving the name Indicopleustes (the Indian traveler). His map (547 A.D.) shows some knowledge of the earth from the Atlantic to India. Such a man would, with hardly a doubt, have observed every numeral system used by the people with whom he sojourned,[329] and whether or not he recorded his studies in permanent form he would have transmitted such scraps of knowledge by word of mouth.
As to the Arabs, it is a mistake to feel that their activities began with Mohammed. Commerce had always been held in honor by them, and the Qoreish[330] had annually for many generations sent caravans bearing the spices and textiles of Yemen to the shores of the Mediterranean. In the fifth century they traded by sea with India and even with China, and Ḥira was an emporium for the wares of the East,[331] so that any numeral system of any part of the trading world could hardly have remained isolated.
Long before the warlike activity of the Arabs, Alexandria had become the great market-place of the world. From this center caravans traversed Arabia to Hadramaut, where they met ships from India. Others went north to Damascus, while still others made their way [83]along the southern shores of the Mediterranean. Ships sailed from the isthmus of Suez to all the commercial ports of Southern Europe and up into the Black Sea. Hindus were found among the merchants[332] who frequented the bazaars of Alexandria, and Brahmins were reported even in Byzantium.
Such is a very brief résumé of the evidence showing that the numerals of the Punjab and of other parts of India as well, and indeed those of China and farther Persia, of Ceylon and the Malay peninsula, might well have been known to the merchants of Alexandria, and even to those of any other seaport of the Mediterranean, in the time of Boethius. The Brāhmī numerals would not have attracted the attention of scholars, for they had no zero so far as we know, and therefore they were no better and no worse than those of dozens of other systems. If Boethius was attracted to them it was probably exactly as any one is naturally attracted to the bizarre or the mystic, and he would have mentioned them in his works only incidentally, as indeed they are mentioned in the manuscripts in which they occur.
In answer therefore to the second question, Could Boethius have known the Hindu numerals? the reply must be, without the slightest doubt, that he could easily have known them, and that it would have been strange if a man of his inquiring mind did not pick up many curious bits of information of this kind even though he never thought of making use of them.
Let us now consider the third question, Is there any positive or strong circumstantial evidence that Boethius did know these numerals? The question is not new, [84]nor is it much nearer being answered than it was over two centuries ago when Wallis (1693) expressed his doubts about it[333] soon after Vossius (1658) had called attention to the matter.[334] Stated briefly, there are three works on mathematics attributed to Boethius:[335] (1) the arithmetic, (2) a work on music, and (3) the geometry.[336]
The genuineness of the arithmetic and the treatise on music is generally recognized, but the geometry, which contains the Hindu numerals with the zero, is under suspicion.[337] There are plenty of supporters of the idea that Boethius knew the numerals and included them in this book,[338] and on the other hand there are as many who [85]feel that the geometry, or at least the part mentioning the numerals, is spurious.[339] The argument of those who deny the authenticity of the particular passage in question may briefly be stated thus:
1. The falsification of texts has always been the subject of complaint. It was so with the Romans,[340] it was common in the Middle Ages,[341] and it is much more prevalent [86]to-day than we commonly think. We have but to see how every hymn-book compiler feels himself authorized to change at will the classics of our language, and how unknown editors have mutilated Shakespeare, to see how much more easy it was for medieval scribes to insert or eliminate paragraphs without any protest from critics.[342]
2. If Boethius had known these numerals he would have mentioned them in his arithmetic, but he does not do so.[343]
3. If he had known them, and had mentioned them in any of his works, his contemporaries, disciples, and successors would have known and mentioned them. But neither Capella (c. 475)[344] nor any of the numerous medieval writers who knew the works of Boethius makes any reference to the system.[345]
4. The passage in question has all the appearance of an interpolation by some scribe. Boethius is speaking of angles, in his work on geometry, when the text suddenly changes to a discussion of classes of numbers.[346] This is followed by a chapter in explanation of the abacus,[347] in which are described those numeral forms which are called apices or caracteres.[348] The forms[349] of these characters vary in different manuscripts, but in general are about as shown on page 88. They are commonly written with the 9 at the left, decreasing to the unit at the right, numerous writers stating that this was because they were derived from Semitic sources in which the direction of writing is the opposite of our own. This practice continued until the sixteenth century.[350] The writer then leaves the subject entirely, using the Roman numerals for the rest of his discussion, a proceeding so foreign to the method of Boethius as to be inexplicable on the hypothesis of authenticity. Why should such a scholarly writer have given them with no mention of their origin or use? Either he would have mentioned some historical interest attaching to them, or he would have used them in some discussion; he certainly would not have left the passage as it is.
 | |
| a [352] | 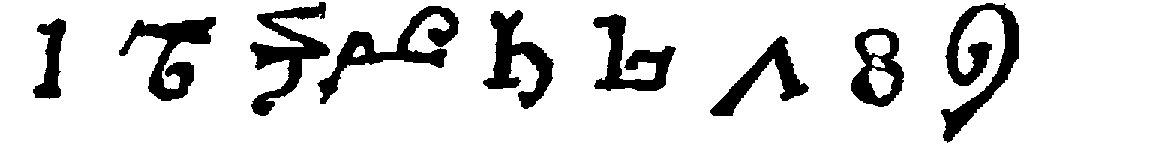 |
| b [353] | 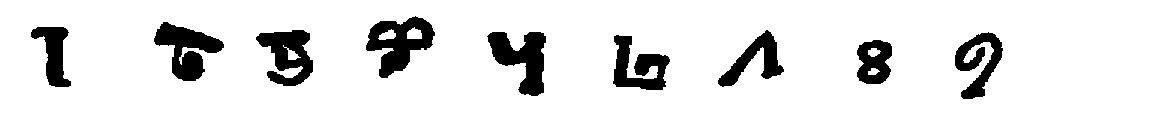 |
| c [354] |  |
| d [355] | 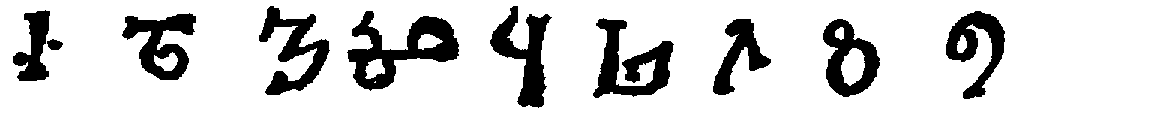 |
| e [356] |  |
| f [357] |  |
| g [358] | 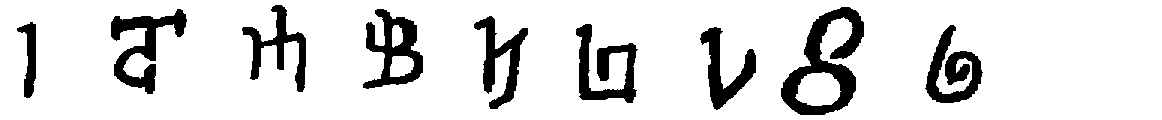 |
| h [359] | 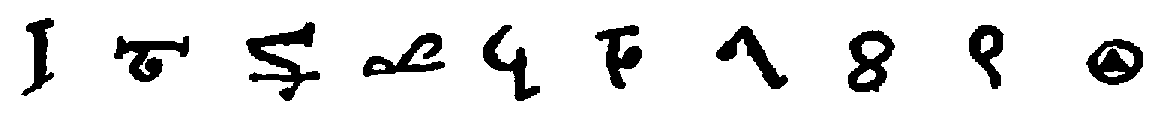 |
| i [360] | 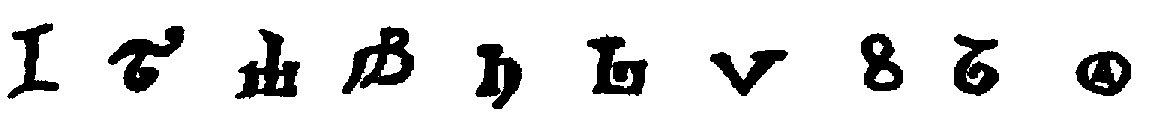 |
Sir E. Clive Bayley has added[361] a further reason for believing them spurious, namely that the 4 is not of the Nānā Ghāt type, but of the Kabul form which the Arabs did not receive until 776;[362] so that it is not likely, even if the characters were known in Europe in the time of Boethius, that this particular form was recognized. It is worthy of mention, also, that in the six abacus forms from the chief manuscripts as given by Friedlein,[363] each contains some form of zero, which symbol probably originated in India about this time or later. It could hardly have reached Europe so soon.
As to the fourth question, Did Boethius probably know the numerals? It seems to be a fair conclusion, according to our present evidence, that (1) Boethius might very easily have known these numerals without the zero, but, (2) there is no reliable evidence that he did know them. And just as Boethius might have come in contact with them, so any other inquiring mind might have done so either in his time or at any time before they definitely appeared in the tenth century. These centuries, five in number, represented the darkest of the Dark Ages, and even if these numerals were occasionally met and studied, no trace of them would be likely to show itself in the [90]literature of the period, unless by chance it should get into the writings of some man like Alcuin. As a matter of fact, it was not until the ninth or tenth century that there is any tangible evidence of their presence in Christendom. They were probably known to merchants here and there, but in their incomplete state they were not of sufficient importance to attract any considerable attention.
As a result of this brief survey of the evidence several conclusions seem reasonable: (1) commerce, and travel for travel's sake, never died out between the East and the West; (2) merchants had every opportunity of knowing, and would have been unreasonably stupid if they had not known, the elementary number systems of the peoples with whom they were trading, but they would not have put this knowledge in permanent written form; (3) wandering scholars would have known many and strange things about the peoples they met, but they too were not, as a class, writers; (4) there is every reason a priori for believing that the ġobār numerals would have been known to merchants, and probably to some of the wandering scholars, long before the Arabs conquered northern Africa; (5) the wonder is not that the Hindu-Arabic numerals were known about 1000 A.D., and that they were the subject of an elaborate work in 1202 by Fibonacci, but rather that more extended manuscript evidence of their appearance before that time has not been found. That they were more or less known early in the Middle Ages, certainly to many merchants of Christian Europe, and probably to several scholars, but without the zero, is hardly to be doubted. The lack of documentary evidence is not at all strange, in view of all of the circumstances.
THE DEVELOPMENT OF THE NUMERALS AMONG THE ARABS
If the numerals had their origin in India, as seems most probable, when did the Arabs come to know of them? It is customary to say that it was due to the influence of Mohammedanism that learning spread through Persia and Arabia; and so it was, in part. But learning was already respected in these countries long before Mohammed appeared, and commerce flourished all through this region. In Persia, for example, the reign of Khosrū Nuśīrwān,[364] the great contemporary of Justinian the law-maker, was characterized not only by an improvement in social and economic conditions, but by the cultivation of letters. Khosrū fostered learning, inviting to his court scholars from Greece, and encouraging the introduction of culture from the West as well as from the East. At this time Aristotle and Plato were translated, and portions of the Hito-padēśa, or Fables of Pilpay, were rendered from the Sanskrit into Persian. All this means that some three centuries before the great intellectual ascendancy of Bagdad a similar fostering of learning was taking place in Persia, and under pre-Mohammedan influences.
The first definite trace that we have of the introduction of the Hindu system into Arabia dates from 773 A.D.,[365] when an Indian astronomer visited the court of the caliph, bringing with him astronomical tables which at the caliph's command were translated into Arabic by Al-Fazārī.[366] Al-Khowārazmī and Ḥabash (Aḥmed ibn ‛Abdallāh, died c. 870) based their well-known tables upon the work of Al-Fāzarī. It may be asserted as highly probable that the numerals came at the same time as the tables. They were certainly known a few decades later, and before 825 A.D., about which time the original of the Algoritmi de numero Indorum was written, as that work makes no pretense of being the first work to treat of the Hindu numerals.
The three writers mentioned cover the period from the end of the eighth to the end of the ninth century. While the historians Al-Maś‛ūdī and Al-Bīrūnī follow quite closely upon the men mentioned, it is well to note again the Arab writers on Hindu arithmetic, contemporary with Al-Khowārazmī, who were mentioned in chapter I, viz. Al-Kindī, Sened ibn ‛Alī, and Al-Ṣūfī.
For over five hundred years Arabic writers and others continued to apply to works on arithmetic the name "Indian." In the tenth century such writers are ‛Abdallāh ibn al-Ḥasan, Abū 'l-Qāsim[367] (died 987 A.D.) of Antioch, and Moḥammed ibn ‛Abdallāh, Abū Naṣr[368] (c. 982), of Kalwādā near Bagdad. Others of the same period or [93]earlier (since they are mentioned in the Fihrist,[369] 987 A.D.), who explicitly use the word "Hindu" or "Indian," are Sinān ibn al-Fatḥ[370] of Ḥarrān, and Ahmed ibn ‛Omar, al-Karābīsī.[371] In the eleventh century come Al-Bīrūnī[372] (973-1048) and ‛Ali ibn Aḥmed, Abū 'l-Ḥasan, Al-Nasawī[373] (c. 1030). The following century brings similar works by Ishāq ibn Yūsuf al-Ṣardafī[374] and Samū'īl ibn Yaḥyā ibn ‛Abbās al-Maġrebī al-Andalusī[375] (c. 1174), and in the thirteenth century are ‛Abdallatīf ibn Yūsuf ibn Moḥammed, Muwaffaq al-Dīn Abū Moḥammed al-Baġdādī[376] (c. 1231), and Ibn al-Bannā.[377]
The Greek monk Maximus Planudes, writing in the first half of the fourteenth century, followed the Arabic usage in calling his work Indian Arithmetic.[378] There were numerous other Arabic writers upon arithmetic, as that subject occupied one of the high places among the sciences, but most of them did not feel it necessary to refer to the origin of the symbols, the knowledge of which might well have been taken for granted.
One document, cited by Woepcke,[379] is of special interest since it shows at an early period, 970 A.D., the use of the ordinary Arabic forms alongside the ġobār. The title of the work is Interesting and Beautiful Problems on Numbers copied by Aḥmed ibn Moḥammed ibn ‛Abdaljalīl, Abū Sa‛īd, al-Sijzī,[380] (951-1024) from a work by a priest and physician, Naẓīf ibn Yumn,[381] al-Qass (died c. 990). Suter does not mention this work of Naẓīf.
The second reason for not ascribing too much credit to the purely Arab influence is that the Arab by himself never showed any intellectual strength. What took place after Moḥammed had lighted the fire in the hearts of his people was just what always takes place when different types of strong races blend,—a great renaissance in divers lines. It was seen in the blending of such types at Miletus in the time of Thales, at Rome in the days of the early invaders, at Alexandria when the Greek set firm foot on Egyptian soil, and we see it now when all the nations mingle their vitality in the New World. So when the Arab culture joined with the Persian, a new civilization rose and flourished.[382] The Arab influence came not from its purity, but from its intermingling with an influence more cultured if less virile.
As a result of this interactivity among peoples of diverse interests and powers, Mohammedanism was to the world from the eighth to the thirteenth century what Rome and Athens and the Italo-Hellenic influence generally had [95]been to the ancient civilization. "If they did not possess the spirit of invention which distinguished the Greeks and the Hindus, if they did not show the perseverance in their observations that characterized the Chinese astronomers, they at least possessed the virility of a new and victorious people, with a desire to understand what others had accomplished, and a taste which led them with equal ardor to the study of algebra and of poetry, of philosophy and of language."[383]
It was in 622 A.D. that Moḥammed fled from Mecca, and within a century from that time the crescent had replaced the cross in Christian Asia, in Northern Africa, and in a goodly portion of Spain. The Arab empire was an ellipse of learning with its foci at Bagdad and Cordova, and its rulers not infrequently took pride in demanding intellectual rather than commercial treasure as the result of conquest.[384]
It was under these influences, either pre-Mohammedan or later, that the Hindu numerals found their way to the North. If they were known before Moḥammed's time, the proof of this fact is now lost. This much, however, is known, that in the eighth century they were taken to Bagdad. It was early in that century that the Mohammedans obtained their first foothold in northern India, thus foreshadowing an epoch of supremacy that endured with varied fortunes until after the golden age of Akbar the Great (1542-1605) and Shah Jehan. They also conquered Khorassan and Afghanistan, so that the learning and the commercial customs of India at once found easy [96]access to the newly-established schools and the bazaars of Mesopotamia and western Asia. The particular paths of conquest and of commerce were either by way of the Khyber Pass and through Kabul, Herat and Khorassan, or by sea through the strait of Ormuz to Basra (Busra) at the head of the Persian Gulf, and thence to Bagdad. As a matter of fact, one form of Arabic numerals, the one now in use by the Arabs, is attributed to the influence of Kabul, while the other, which eventually became our numerals, may very likely have reached Arabia by the other route. It is in Bagdad,[385] Dār al-Salām—"the Abode of Peace," that our special interest in the introduction of the numerals centers. Built upon the ruins of an ancient town by Al-Manṣūr[386] in the second half of the eighth century, it lies in one of those regions where the converging routes of trade give rise to large cities.[387] Quite as well of Bagdad as of Athens might Cardinal Newman have said:[388]
"What it lost in conveniences of approach, it gained in its neighborhood to the traditions of the mysterious East, and in the loveliness of the region in which it lay. Hither, then, as to a sort of ideal land, where all archetypes of the great and the fair were found in substantial being, and all departments of truth explored, and all diversities of intellectual power exhibited, where taste and philosophy were majestically enthroned as in a royal court, where there was no sovereignty but that of mind, and no nobility but that of genius, where professors were [97]rulers, and princes did homage, thither flocked continually from the very corners of the orbis terrarum the many-tongued generation, just rising, or just risen into manhood, in order to gain wisdom." For here it was that Al-Manṣūr and Al-Māmūn and Hārūn al-Rashīd (Aaron the Just) made for a time the world's center of intellectual activity in general and in the domain of mathematics in particular.[389] It was just after the Sindhind was brought to Bagdad that Moḥammed ibn Mūsā al-Khowārazmī, whose name has already been mentioned,[390] was called to that city. He was the most celebrated mathematician of his time, either in the East or West, writing treatises on arithmetic, the sundial, the astrolabe, chronology, geometry, and algebra, and giving through the Latin transliteration of his name, algoritmi, the name of algorism to the early arithmetics using the new Hindu numerals.[391] Appreciating at once the value of the position system so recently brought from India, he wrote an arithmetic based upon these numerals, and this was translated into Latin in the time of Adelhard of Bath (c. 1180), although possibly by his contemporary countryman Robert Cestrensis.[392] This translation was found in Cambridge and was published by Boncompagni in 1857.[393]
Contemporary with Al-Khowārazmī, and working also under Al-Māmūn, was a Jewish astronomer, Abū 'l-Ṭeiyib, [98]Sened ibn ‛Alī, who is said to have adopted the Mohammedan religion at the caliph's request. He also wrote a work on Hindu arithmetic,[394] so that the subject must have been attracting considerable attention at that time. Indeed, the struggle to have the Hindu numerals replace the Arabic did not cease for a long time thereafter. ‛Alī ibn Aḥmed al-Nasawī, in his arithmetic of c. 1025, tells us that the symbolism of number was still unsettled in his day, although most people preferred the strictly Arabic forms.[395]
We thus have the numerals in Arabia, in two forms: one the form now used there, and the other the one used by Al-Khowārazmī. The question then remains, how did this second form find its way into Europe? and this question will be considered in the next chapter.
THE DEFINITE INTRODUCTION OF THE NUMERALS INTO EUROPE
It being doubtful whether Boethius ever knew the Hindu numeral forms, certainly without the zero in any case, it becomes necessary now to consider the question of their definite introduction into Europe. From what has been said of the trade relations between the East and the West, and of the probability that it was the trader rather than the scholar who carried these numerals from their original habitat to various commercial centers, it is evident that we shall never know when they first made their inconspicuous entrance into Europe. Curious customs from the East and from the tropics,—concerning games, social peculiarities, oddities of dress, and the like,—are continually being related by sailors and traders in their resorts in New York, London, Hamburg, and Rotterdam to-day, customs that no scholar has yet described in print and that may not become known for many years, if ever. And if this be so now, how much more would it have been true a thousand years before the invention of printing, when learning was at its lowest ebb. It was at this period of low esteem of culture that the Hindu numerals undoubtedly made their first appearance in Europe.
There were many opportunities for such knowledge to reach Spain and Italy. In the first place the Moors went into Spain as helpers of a claimant of the throne, and [100]remained as conquerors. The power of the Goths, who had held Spain for three centuries, was shattered at the battle of Jerez de la Frontera in 711, and almost immediately the Moors became masters of Spain and so remained for five hundred years, and masters of Granada for a much longer period. Until 850 the Christians were absolutely free as to religion and as to holding political office, so that priests and monks were not infrequently skilled both in Latin and Arabic, acting as official translators, and naturally reporting directly or indirectly to Rome. There was indeed at this time a complaint that Christian youths cultivated too assiduously a love for the literature of the Saracen, and married too frequently the daughters of the infidel.[396] It is true that this happy state of affairs was not permanent, but while it lasted the learning and the customs of the East must have become more or less the property of Christian Spain. At this time the ġobār numerals were probably in that country, and these may well have made their way into Europe from the schools of Cordova, Granada, and Toledo.
Furthermore, there was abundant opportunity for the numerals of the East to reach Europe through the journeys of travelers and ambassadors. It was from the records of Suleimān the Merchant, a well-known Arab trader of the ninth century, that part of the story of Sindbād the Sailor was taken.[397] Such a merchant would have been particularly likely to know the numerals of the people whom he met, and he is a type of man that may well have taken such symbols to European markets. A little later, [101]Abū 'l-Ḥasan ‛Alī al-Mas‛ūdī (d. 956) of Bagdad traveled to the China Sea on the east, at least as far south as Zanzibar, and to the Atlantic on the west,[398] and he speaks of the nine figures with which the Hindus reckoned.[399]
There was also a Bagdad merchant, one Abū 'l-Qāsim ‛Obeidallāh ibn Aḥmed, better known by his Persian name Ibn Khordāḍbeh,[400] who wrote about 850 A.D. a work entitled Book of Roads and Provinces[401] in which the following graphic account appears:[402] "The Jewish merchants speak Persian, Roman (Greek and Latin), Arabic, French, Spanish, and Slavic. They travel from the West to the East, and from the East to the West, sometimes by land, sometimes by sea. They take ship from France on the Western Sea, and they voyage to Farama (near the ruins of the ancient Pelusium); there they transfer their goods to caravans and go by land to Colzom (on the Red Sea). They there reëmbark on the Oriental (Red) Sea and go to Hejaz and to Jiddah, and thence to the Sind, India, and China. Returning, they bring back the products of the oriental lands.... These journeys are also made by land. The merchants, leaving France and Spain, cross to Tangier and thence pass through the African provinces and Egypt. They then go to Ramleh, visit Damascus, Kufa, Bagdad, and Basra, penetrate into Ahwaz, Fars, Kerman, Sind, and thus reach India and China." Such travelers, about 900 A.D., must necessarily have spread abroad a knowledge of all number [102]systems used in recording prices or in the computations of the market. There is an interesting witness to this movement, a cruciform brooch now in the British Museum. It is English, certainly as early as the eleventh century, but it is inlaid with a piece of paste on which is the Mohammedan inscription, in Kufic characters, "There is no God but God." How did such an inscription find its way, perhaps in the time of Alcuin of York, to England? And if these Kufic characters reached there, then why not the numeral forms as well?
Even in literature of the better class there appears now and then some stray proof of the important fact that the great trade routes to the far East were never closed for long, and that the customs and marks of trade endured from generation to generation. The Gulistān of the Persian poet Sa‛dī[403] contains such a passage:
"I met a merchant who owned one hundred and forty camels, and fifty slaves and porters.... He answered to me: 'I want to carry sulphur of Persia to China, which in that country, as I hear, bears a high price; and thence to take Chinese ware to Roum; and from Roum to load up with brocades for Hind; and so to trade Indian steel (pûlab) to Halib. From Halib I will convey its glass to Yeman, and carry the painted cloths of Yeman back to Persia.'"[404] On the other hand, these men were not of the learned class, nor would they preserve in treatises any knowledge that they might have, although this knowledge would occasionally reach the ears of the learned as bits of curious information.
There were also ambassadors passing back and forth from time to time, between the East and the West, and in particular during the period when these numerals probably began to enter Europe. Thus Charlemagne (c. 800) sent emissaries to Bagdad just at the time of the opening of the mathematical activity there.[405] And with such ambassadors must have gone the adventurous scholar, inspired, as Alcuin says of Archbishop Albert of York (766-780),[406] to seek the learning of other lands. Furthermore, the Nestorian communities, established in Eastern Asia and in India at this time, were favored both by the Persians and by their Mohammedan conquerors. The Nestorian Patriarch of Syria, Timotheus (778-820), sent missionaries both to India and to China, and a bishop was appointed for the latter field. Ibn Wahab, who traveled to China in the ninth century, found images of Christ and the apostles in the Emperor's court.[407] Such a learned body of men, knowing intimately the countries in which they labored, could hardly have failed to make strange customs known as they returned to their home stations. Then, too, in Alfred's time (849-901) emissaries went [104]from England as far as India,[408] and generally in the Middle Ages groceries came to Europe from Asia as now they come from the colonies and from America. Syria, Asia Minor, and Cyprus furnished sugar and wool, and India yielded her perfumes and spices, while rich tapestries for the courts and the wealthy burghers came from Persia and from China.[409] Even in the time of Justinian (c. 550) there seems to have been a silk trade with China, which country in turn carried on commerce with Ceylon,[410] and reached out to Turkestan where other merchants transmitted the Eastern products westward. In the seventh century there was a well-defined commerce between Persia and India, as well as between Persia and Constantinople.[411] The Byzantine commerciarii were stationed at the outposts not merely as customs officers but as government purchasing agents.[412]
Occasionally there went along these routes of trade men of real learning, and such would surely have carried the knowledge of many customs back and forth. Thus at a period when the numerals are known to have been partly understood in Italy, at the opening of the eleventh century, one Constantine, an African, traveled from Italy through a great part of Africa and Asia, even on to India, for the purpose of learning the sciences of the Orient. He spent thirty-nine years in travel, having been hospitably received in Babylon, and upon his return he was welcomed with great honor at Salerno.[413]
A very interesting illustration of this intercourse also appears in the tenth century, when the son of Otto I [105](936-973) married a princess from Constantinople. This monarch was in touch with the Moors of Spain and invited to his court numerous scholars from abroad,[414] and his intercourse with the East as well as the West must have brought together much of the learning of each.
Another powerful means for the circulation of mysticism and philosophy, and more or less of culture, took its start just before the conversion of Constantine (c. 312), in the form of Christian pilgrim travel. This was a feature peculiar to the zealots of early Christianity, found in only a slight degree among their Jewish predecessors in the annual pilgrimage to Jerusalem, and almost wholly wanting in other pre-Christian peoples. Chief among these early pilgrims were the two Placentians, John and Antonine the Elder (c. 303), who, in their wanderings to Jerusalem, seem to have started a movement which culminated centuries later in the crusades.[415] In 333 a Bordeaux pilgrim compiled the first Christian guide-book, the Itinerary from Bordeaux to Jerusalem,[416] and from this time on the holy pilgrimage never entirely ceased.
Still another certain route for the entrance of the numerals into Christian Europe was through the pillaging and trading carried on by the Arabs on the northern shores of the Mediterranean. As early as 652 A.D., in the thirtieth year of the Hejira, the Mohammedans descended upon the shores of Sicily and took much spoil. Hardly had the wretched Constans given place to the [106]young Constantine IV when they again attacked the island and plundered ancient Syracuse. Again in 827, under Asad, they ravaged the coasts. Although at this time they failed to conquer Syracuse, they soon held a good part of the island, and a little later they successfully besieged the city. Before Syracuse fell, however, they had plundered the shores of Italy, even to the walls of Rome itself; and had not Leo IV, in 849, repaired the neglected fortifications, the effects of the Moslem raid of that year might have been very far-reaching. Ibn Khordāḍbeh, who left Bagdad in the latter part of the ninth century, gives a picture of the great commercial activity at that time in the Saracen city of Palermo. In this same century they had established themselves in Piedmont, and in 906 they pillaged Turin.[417] On the Sorrento peninsula the traveler who climbs the hill to the beautiful Ravello sees still several traces of the Arab architecture, reminding him of the fact that about 900 A.D. Amalfi was a commercial center of the Moors.[418] Not only at this time, but even a century earlier, the artists of northern India sold their wares at such centers, and in the courts both of Hārūn al-Rashīd and of Charlemagne.[419] Thus the Arabs dominated the Mediterranean Sea long before Venice
"held the gorgeous East in fee
And was the safeguard of the West,"
and long before Genoa had become her powerful rival.[420]
Only a little later than this the brothers Nicolo and Maffeo Polo entered upon their famous wanderings.[421] Leaving Constantinople in 1260, they went by the Sea of Azov to Bokhara, and thence to the court of Kublai Khan, penetrating China, and returning by way of Acre in 1269 with a commission which required them to go back to China two years later. This time they took with them Nicolo's son Marco, the historian of the journey, and went across the plateau of Pamir; they spent about twenty years in China, and came back by sea from China to Persia.
The ventures of the Poli were not long unique, however: the thirteenth century had not closed before Roman missionaries and the merchant Petrus de Lucolongo had penetrated China. Before 1350 the company of missionaries was large, converts were numerous, churches and Franciscan convents had been organized in the East, travelers were appealing for the truth of their accounts to the "many" persons in Venice who had been in China, Tsuan-chau-fu had a European merchant community, and Italian trade and travel to China was a thing that occupied two chapters of a commercial handbook.[422]
It is therefore reasonable to conclude that in the Middle Ages, as in the time of Boethius, it was a simple matter for any inquiring scholar to become acquainted with such numerals of the Orient as merchants may have used for warehouse or price marks. And the fact that Gerbert seems to have known only the forms of the simplest of these, not comprehending their full significance, seems to prove that he picked them up in just this way.
Even if Gerbert did not bring his knowledge of the Oriental numerals from Spain, he may easily have obtained them from the marks on merchant's goods, had he been so inclined. Such knowledge was probably obtainable in various parts of Italy, though as parts of mere mercantile knowledge the forms might soon have been lost, it needing the pen of the scholar to preserve them. Trade at this time was not stagnant. During the eleventh and twelfth centuries the Slavs, for example, had very great commercial interests, their trade reaching to Kiev and Novgorod, and thence to the East. Constantinople was a great clearing-house of commerce with the Orient,[423] and the Byzantine merchants must have been entirely familiar with the various numerals of the Eastern peoples. In the eleventh century the Italian town of Amalfi established a factory[424] in Constantinople, and had trade relations with Antioch and Egypt. Venice, as early as the ninth century, had a valuable trade with Syria and Cairo.[425] Fifty years after Gerbert died, in the time of Cnut, the Dane and the Norwegian pushed their commerce far beyond the northern seas, both by caravans through Russia to the Orient, and by their venturesome barks which [109]sailed through the Strait of Gibraltar into the Mediterranean.[426] Only a little later, probably before 1200 A.D., a clerk in the service of Thomas à Becket, present at the latter's death, wrote a life of the martyr, to which (fortunately for our purposes) he prefixed a brief eulogy of the city of London.[427] This clerk, William Fitz Stephen by name, thus speaks of the British capital:
Aurum mittit Arabs: species et thura Sabæus:
Arma Sythes: oleum palmarum divite sylva
Pingue solum Babylon: Nilus lapides pretiosos:
Norwegi, Russi, varium grisum, sabdinas:
Seres, purpureas vestes: Galli, sua vina.
Although, as a matter of fact, the Arabs had no gold to send, and the Scythians no arms, and Egypt no precious stones save only the turquoise, the Chinese (Seres) may have sent their purple vestments, and the north her sables and other furs, and France her wines. At any rate the verses show very clearly an extensive foreign trade.
Then there were the Crusades, which in these times brought the East in touch with the West. The spirit of the Orient showed itself in the songs of the troubadours, and the baudekin,[428] the canopy of Bagdad,[429] became common in the churches of Italy. In Sicily and in Venice the textile industries of the East found place, and made their way even to the Scandinavian peninsula.[430]
We therefore have this state of affairs: There was abundant intercourse between the East and West for [110]some centuries before the Hindu numerals appear in any manuscripts in Christian Europe. The numerals must of necessity have been known to many traders in a country like Italy at least as early as the ninth century, and probably even earlier, but there was no reason for preserving them in treatises. Therefore when a man like Gerbert made them known to the scholarly circles, he was merely describing what had been familiar in a small way to many people in a different walk of life.
Since Gerbert[431] was for a long time thought to have been the one to introduce the numerals into Italy,[432] a brief sketch of this unique character is proper. Born of humble parents,[433] this remarkable man became the counselor and companion of kings, and finally wore the papal tiara as Sylvester II, from 999 until his death in 1003.[434] He was early brought under the influence of the monks at Aurillac, and particularly of Raimund, who had been a pupil of Odo of Cluny, and there in due time he himself took holy orders. He visited Spain in about 967 in company with Count Borel,[435] remaining there three years, [111]and studying under Bishop Hatto of Vich,[436] a city in the province of Barcelona,[437] then entirely under Christian rule. Indeed, all of Gerbert's testimony is as to the influence of the Christian civilization upon his education. Thus he speaks often of his study of Boethius,[438] so that if the latter knew the numerals Gerbert would have learned them from him.[439] If Gerbert had studied in any Moorish schools he would, under the decree of the emir Hishām (787-822), have been obliged to know Arabic, which would have taken most of his three years in Spain, and of which study we have not the slightest hint in any of his letters.[440] On the other hand, Barcelona was the only Christian province in immediate touch with the Moorish civilization at that time.[441] Furthermore we know that earlier in the same century King Alonzo of Asturias (d. 910) confided the education of his son Ordoño to the Arab scholars of the court of the [112]wālī of Saragossa,[442] so that there was more or less of friendly relation between Christian and Moor.
After his three years in Spain, Gerbert went to Italy, about 970, where he met Pope John XIII, being by him presented to the emperor Otto I. Two years later (972), at the emperor's request, he went to Rheims, where he studied philosophy, assisting to make of that place an educational center; and in 983 he became abbot at Bobbio. The next year he returned to Rheims, and became archbishop of that diocese in 991. For political reasons he returned to Italy in 996, became archbishop of Ravenna in 998, and the following year was elected to the papal chair. Far ahead of his age in wisdom, he suffered as many such scholars have even in times not so remote by being accused of heresy and witchcraft. As late as 1522, in a biography published at Venice, it is related that by black art he attained the papacy, after having given his soul to the devil.[443] Gerbert was, however, interested in astrology,[444] although this was merely the astronomy of that time and was such a science as any learned man would wish to know, even as to-day we wish to be reasonably familiar with physics and chemistry.
That Gerbert and his pupils knew the ġobār numerals is a fact no longer open to controversy.[445] Bernelinus and Richer[446] call them by the well-known name of [113]"caracteres," a word used by Radulph of Laon in the same sense a century later.[447] It is probable that Gerbert was the first to describe these ġobār numerals in any scientific way in Christian Europe, but without the zero. If he knew the latter he certainly did not understand its use.[448]
The question still to be settled is as to where he found these numerals. That he did not bring them from Spain is the opinion of a number of careful investigators.[449] This is thought to be the more probable because most of the men who made Spain famous for learning lived after Gerbert was there. Such were Ibn Sīnā (Avicenna) who lived at the beginning, and Gerber of Seville who flourished in the middle, of the eleventh century, and Abū Roshd (Averroës) who lived at the end of the twelfth.[450] Others hold that his proximity to [114]the Arabs for three years makes it probable that he assimilated some of their learning, in spite of the fact that the lines between Christian and Moor at that time were sharply drawn.[451] Writers fail, however, to recognize that a commercial numeral system would have been more likely to be made known by merchants than by scholars. The itinerant peddler knew no forbidden pale in Spain, any more than he has known one in other lands. If the ġobār numerals were used for marking wares or keeping simple accounts, it was he who would have known them, and who would have been the one rather than any Arab scholar to bring them to the inquiring mind of the young French monk. The facts that Gerbert knew them only imperfectly, that he used them solely for calculations, and that the forms are evidently like the Spanish ġobār, make it all the more probable that it was through the small tradesman of the Moors that this versatile scholar derived his knowledge. Moreover the part of the geometry bearing his name, and that seems unquestionably his, shows the Arab influence, proving that he at least came into contact with the transplanted Oriental learning, even though imperfectly.[452] There was also the persistent Jewish merchant trading with both peoples then as now, always alive to the acquiring of useful knowledge, and it would be very natural for a man like Gerbert to welcome learning from such a source.
On the other hand, the two leading sources of information as to the life of Gerbert reveal practically nothing to show that he came within the Moorish sphere of influence during his sojourn in Spain. These sources [115]are his letters and the history written by Richer. Gerbert was a master of the epistolary art, and his exalted position led to the preservation of his letters to a degree that would not have been vouchsafed even by their classic excellence.[453] Richer was a monk at St. Remi de Rheims, and was doubtless a pupil of Gerbert. The latter, when archbishop of Rheims, asked Richer to write a history of his times, and this was done. The work lay in manuscript, entirely forgotten until Pertz discovered it at Bamberg in 1833.[454] The work is dedicated to Gerbert as archbishop of Rheims,[455] and would assuredly have testified to such efforts as he may have made to secure the learning of the Moors.
Now it is a fact that neither the letters nor this history makes any statement as to Gerbert's contact with the Saracens. The letters do not speak of the Moors, of the Arab numerals, nor of Cordova. Spain is not referred to by that name, and only one Spanish scholar is mentioned. In one of his letters he speaks of Joseph Ispanus,[456] or Joseph Sapiens, but who this Joseph the Wise of Spain may have been we do not know. Possibly [116]it was he who contributed the morsel of knowledge so imperfectly assimilated by the young French monk.[457] Within a few years after Gerbert's visit two young Spanish monks of lesser fame, and doubtless with not that keen interest in mathematical matters which Gerbert had, regarded the apparently slight knowledge which they had of the Hindu numeral forms as worthy of somewhat permanent record[458] in manuscripts which they were transcribing. The fact that such knowledge had penetrated to their modest cloisters in northern Spain—the one Albelda or Albaida—indicates that it was rather widely diffused.
Gerbert's treatise Libellus de numerorum divisione[459] is characterized by Chasles as "one of the most obscure documents in the history of science."[460] The most complete information in regard to this and the other mathematical works of Gerbert is given by Bubnov,[461] who considers this work to be genuine.[462]
So little did Gerbert appreciate these numerals that in his works known as the Regula de abaco computi and the Libellus he makes no use of them at all, employing only the Roman forms.[463] Nevertheless Bernelinus[464] refers to the nine ġobār characters.[465] These Gerbert had marked on a thousand jetons or counters,[466] using the latter on an abacus which he had a sign-maker prepare for him.[467] Instead of putting eight counters in say the tens' column, Gerbert would put a single counter marked 8, and so for the other places, leaving the column empty where we would place a zero, but where he, lacking the zero, had no counter to place. These counters he possibly called caracteres, a name which adhered also to the figures themselves. It is an interesting speculation to consider whether these apices, as they are called in the Boethius interpolations, were in any way suggested by those Roman jetons generally known in numismatics as tesserae, and bearing the figures I-XVI, the sixteen referring to the number of assi in a sestertius.[468] The [118]name apices adhered to the Hindu-Arabic numerals until the sixteenth century.[469]
To the figures on the apices were given the names Igin, andras, ormis, arbas, quimas, calctis or caltis, zenis, temenias, celentis, sipos,[470] the origin and meaning of which still remain a mystery. The Semitic origin of several of the words seems probable. Wahud, thaneine, [119]thalata, arba, kumsa, setta, sebba, timinia, taseud are given by the Rev. R. Patrick[471] as the names, in an Arabic dialect used in Morocco, for the numerals from one to nine. Of these the words for four, five, and eight are strikingly like those given above.
The name apices was not, however, a common one in later times. Notae was more often used, and it finally gave the name to notation.[472] Still more common were the names figures, ciphers, signs, elements, and characters.[473]
So little effect did the teachings of Gerbert have in making known the new numerals, that O'Creat, who lived a century later, a friend and pupil of Adelhard [120]of Bath, used the zero with the Roman characters, in contrast to Gerbert's use of the ġobār forms without the zero.[474] O'Creat uses three forms for zero, o, ō, and τ, as in Maximus Planudes. With this use of the zero goes, naturally, a place value, for he writes III III for 33, ICCOO and I. II. τ. τ for 1200, I. O. VIII. IX for 1089, and I. IIII. IIII. ττττ for the square of 1200.
The period from the time of Gerbert until after the appearance of Leonardo's monumental work may be called the period of the abacists. Even for many years after the appearance early in the twelfth century of the books explaining the Hindu art of reckoning, there was strife between the abacists, the advocates of the abacus, and the algorists, those who favored the new numerals. The words cifra and algorismus cifra were used with a somewhat derisive significance, indicative of absolute uselessness, as indeed the zero is useless on an abacus in which the value of any unit is given by the column which it occupies.[475] So Gautier de Coincy (1177-1236) in a work on the miracles of Mary says:
A horned beast, a sheep,
An algorismus-cipher,
Is a priest, who on such a feast day
Does not celebrate the holy Mother.[476]
So the abacus held the field for a long time, even against the new algorism employing the new numerals. [121]Geoffrey Chaucer[477] describes in The Miller's Tale the clerk with
"His Almageste and bokes grete and smale,
His astrelabie, longinge for his art,
His augrim-stones layen faire apart
On shelves couched at his beddes heed."
So, too, in Chaucer's explanation of the astrolabe,[478] written for his son Lewis, the number of degrees is expressed on the instrument in Hindu-Arabic numerals: "Over the whiche degrees ther ben noumbres of augrim, that devyden thilke same degrees fro fyve to fyve," and "... the nombres ... ben writen in augrim," meaning in the way of the algorism. Thomas Usk about 1387 writes:[479] "a sypher in augrim have no might in signification of it-selve, yet he yeveth power in signification to other." So slow and so painful is the assimilation of new ideas.
Bernelinus[480] states that the abacus is a well-polished board (or table), which is covered with blue sand and used by geometers in drawing geometrical figures. We have previously mentioned the fact that the Hindus also performed mathematical computations in the sand, although there is no evidence to show that they had any column abacus.[481] For the purposes of computation, Bernelinus continues, the board is divided into thirty vertical columns, three of which are reserved for fractions. Beginning with the units columns, each set of [122]three columns (lineae is the word which Bernelinus uses) is grouped together by a semicircular arc placed above them, while a smaller arc is placed over the units column and another joins the tens and hundreds columns. Thus arose the designation arcus pictagore[482] or sometimes simply arcus.[483] The operations of addition, subtraction, and multiplication upon this form of the abacus required little explanation, although they were rather extensively treated, especially the multiplication of different orders of numbers. But the operation of division was effected with some difficulty. For the explanation of the method of division by the use of the complementary difference,[484] long the stumbling-block in the way of the medieval arithmetician, the reader is referred to works on the history of mathematics[485] and to works relating particularly to the abacus.[486]
Among the writers on the subject may be mentioned Abbo[487] of Fleury (c. 970), Heriger[488] of Lobbes or Laubach [123](c. 950-1007), and Hermannus Contractus[489] (1013-1054), all of whom employed only the Roman numerals. Similarly Adelhard of Bath (c. 1130), in his work Regulae Abaci,[490] gives no reference to the new numerals, although it is certain that he knew them. Other writers on the abacus who used some form of Hindu numerals were Gerland[491] (first half of twelfth century) and Turchill[492] (c. 1200). For the forms used at this period the reader is referred to the plate on page 88.
After Gerbert's death, little by little the scholars of Europe came to
know the new figures, chiefly through the introduction of Arab learning.
The Dark Ages had passed, although arithmetic did not find another
advocate as prominent as Gerbert for two centuries. Speaking of this
great revival, Raoul Glaber[493] (985-c. 1046), a monk of the great
Benedictine abbey of Cluny, of the eleventh century, says: "It was as
though the world had arisen and tossed aside the worn-out garments of
ancient time, and wished to apparel itself in a white robe of churches."
And with this activity in religion came a corresponding interest in other
lines. Algorisms began to appear, and knowledge from the outside world
found [124]interested listeners. Another Raoul, or
Radulph, to whom we have referred as Radulph of Laon,[494] a teacher in the cloister school of
his city, and the brother of Anselm of Laon[495] the celebrated theologian, wrote a
treatise on music, extant but unpublished, and an arithmetic which Nagl
first published in 1890.[496] The latter work, preserved to us in a
parchment manuscript of seventy-seven leaves, contains a curious mixture
of Roman and ġobār numerals, the former for expressing large
results, the latter for practical calculation. These ġobār
"caracteres" include the sipos (zero),  , of which, however, Radulph did not know the full significance;
showing that at the opening of the twelfth century the system was still
uncertain in its status in the church schools of central France.
, of which, however, Radulph did not know the full significance;
showing that at the opening of the twelfth century the system was still
uncertain in its status in the church schools of central France.
At the same time the words algorismus and cifra were coming into general use even in non-mathematical literature. Jordan [497] cites numerous instances of such use from the works of Alanus ab Insulis[498] (Alain de Lille), Gautier de Coincy (1177-1236), and others.
Another contributor to arithmetic during this interesting period was a prominent Spanish Jew called variously John of Luna, John of Seville, Johannes Hispalensis, Johannes Toletanus, and Johannes Hispanensis de Luna.[499] [125]His date is rather closely fixed by the fact that he dedicated a work to Raimund who was archbishop of Toledo between 1130 and 1150.[500] His interests were chiefly in the translation of Arabic works, especially such as bore upon the Aristotelian philosophy. From the standpoint of arithmetic, however, the chief interest centers about a manuscript entitled Joannis Hispalensis liber Algorismi de Practica Arismetrice which Boncompagni found in what is now the Bibliothèque nationale at Paris. Although this distinctly lays claim to being Al-Khowārazmī's work,[501] the evidence is altogether against the statement,[502] but the book is quite as valuable, since it represents the knowledge of the time in which it was written. It relates to the operations with integers and sexagesimal fractions, including roots, and contains no applications.[503]
Contemporary with John of Luna, and also living in Toledo, was Gherard of Cremona,[504] who has sometimes been identified, but erroneously, with Gernardus,[505] the [126]author of a work on algorism. He was a physician, an astronomer, and a mathematician, translating from the Arabic both in Italy and in Spain. In arithmetic he was influential in spreading the ideas of algorism.
Four Englishmen—Adelhard of Bath (c. 1130), Robert of Chester (Robertus Cestrensis, c. 1143), William Shelley, and Daniel Morley (1180)—are known[506] to have journeyed to Spain in the twelfth century for the purpose of studying mathematics and Arabic. Adelhard of Bath made translations from Arabic into Latin of Al-Khowārazmī's astronomical tables[507] and of Euclid's Elements,[508] while Robert of Chester is known as the translator of Al-Khowārazmī's algebra.[509] There is no reason to doubt that all of these men, and others, were familiar with the numerals which the Arabs were using.
The earliest trace we have of computation with Hindu numerals in
Germany is in an Algorismus of 1143, now in the Hofbibliothek in
Vienna.[510] It is bound
in with a [127]Computus by the same author and
bearing the date given. It contains chapters "De additione," "De
diminutione," "De mediatione," "De divisione," and part of a chapter on
multiplication. The numerals are in the usual medieval forms except the 2
which, as will be seen from the illustration,[511] is somewhat different, and the 3,
which takes the peculiar shape 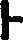 , a form characteristic of the twelfth century.
, a form characteristic of the twelfth century.
It was about the same time that the Sefer ha-Mispar,[512] the Book of Number, appeared in the Hebrew language. The author, Rabbi Abraham ibn Meïr ibn Ezra,[513] was born in Toledo (c. 1092). In 1139 he went to Egypt, Palestine, and the Orient, spending also some years in Italy. Later he lived in southern France and in England. He died in 1167. The probability is that he acquired his knowledge of the Hindu arithmetic[514] in his native town of Toledo, but it is also likely that the knowledge of other systems which he acquired on travels increased his appreciation of this one. We have mentioned the fact that he used the first letters of the Hebrew alphabet, א ב ג ד ה ו ז ח ט, for the numerals 9 8 7 6 5 4 3 2 1, and a circle for the zero. The quotation in the note given below shows that he knew of the Hindu origin; but in his manuscript, although he set down the Hindu forms, he used the above nine Hebrew letters with place value for all computations.
THE SPREAD OF THE NUMERALS IN EUROPE
Of all the medieval writers, probably the one most influential in introducing the new numerals to the scholars of Europe was Leonardo Fibonacci, of Pisa.[515] This remarkable man, the most noteworthy mathematical genius of the Middle Ages, was born at Pisa about 1175.[516]
The traveler of to-day may cross the Via Fibonacci on his way to the Campo Santo, and there he may see at the end of the long corridor, across the quadrangle, the statue of Leonardo in scholars garb. Few towns have honored a mathematician more, and few mathematicians have so distinctly honored their birthplace. Leonardo was born in the golden age of this city, the period of its commercial, religious, and intellectual prosperity.[517] [129]Situated practically at the mouth of the Arno, Pisa formed with Genoa and Venice the trio of the greatest commercial centers of Italy at the opening of the thirteenth century. Even before Venice had captured the Levantine trade, Pisa had close relations with the East. An old Latin chronicle relates that in 1005 "Pisa was captured by the Saracens," that in the following year "the Pisans overthrew the Saracens at Reggio," and that in 1012 "the Saracens came to Pisa and destroyed it." The city soon recovered, however, sending no fewer than a hundred and twenty ships to Syria in 1099,[518] founding a merchant colony in Constantinople a few years later,[519] and meanwhile carrying on an interurban warfare in Italy that seemed to stimulate it to great activity.[520] A writer of 1114 tells us that at that time there were many heathen people—Turks, Libyans, Parthians, and Chaldeans—to be found in Pisa. It was in the midst of such wars, in a cosmopolitan and commercial town, in a center where literary work was not appreciated,[521] that the genius of Leonardo appears as one of the surprises of history, warning us again that "we should draw no horoscope; that we should expect little, for what we expect will not come to pass."[522]
Leonardo's father was one William,[523] and he had a brother named Bonaccingus,[524] but nothing further is [130]known of his family. As to Fibonacci, most writers[525] have assumed that his father's name was Bonaccio,[526] whence filius Bonaccii, or Fibonacci. Others[527] believe that the name, even in the Latin form of filius Bonaccii as used in Leonardo's work, was simply a general one, like our Johnson or Bronson (Brown's son); and the only contemporary evidence that we have bears out this view. As to the name Bigollo, used by Leonardo, some have thought it a self-assumed one meaning blockhead, a term that had been applied to him by the commercial world or possibly by the university circle, and taken by him that he might prove what a blockhead could do. Milanesi,[528] however, has shown that the word Bigollo (or Pigollo) was used in Tuscany to mean a traveler, and was naturally assumed by one who had studied, as Leonardo had, in foreign lands.
Leonardo's father was a commercial agent at Bugia, the modern Bougie,[529] the ancient Saldae on the coast of Barbary,[530] a royal capital under the Vandals and again, a century before Leonardo, under the Beni Hammad. It had one of the best harbors on the coast, sheltered as it is by Mt. Lalla Guraia,[531] and at the close of the twelfth century it was a center of African commerce. It was here that Leonardo was taken as a child, and here he went to school to a Moorish master. When he reached the years of young manhood he started on a tour of the Mediterranean Sea, and visited Egypt, Syria, Greece, Sicily, and Provence, meeting with scholars as well as with [131]merchants, and imbibing a knowledge of the various systems of numbers in use in the centers of trade. All these systems, however, he says he counted almost as errors compared with that of the Hindus.[532] Returning to Pisa, he wrote his Liber Abaci[533] in 1202, rewriting it in 1228.[534] In this work the numerals are explained and are used in the usual computations of business. Such a treatise was not destined to be popular, however, because it was too advanced for the mercantile class, and too novel for the conservative university circles. Indeed, at this time mathematics had only slight place in the newly established universities, as witness the oldest known statute of the Sorbonne at Paris, dated 1215, where the subject is referred to only in an incidental way.[535] The period was one of great commercial activity, and on this very [132]account such a book would attract even less attention than usual.[536]
It would now be thought that the western world would at once adopt the new numerals which Leonardo had made known, and which were so much superior to anything that had been in use in Christian Europe. The antagonism of the universities would avail but little, it would seem, against such an improvement. It must be remembered, however, that there was great difficulty in spreading knowledge at this time, some two hundred and fifty years before printing was invented. "Popes and princes and even great religious institutions possessed far fewer books than many farmers of the present age. The library belonging to the Cathedral Church of San Martino at Lucca in the ninth century contained only nineteen volumes of abridgments from ecclesiastical commentaries."[537] Indeed, it was not until the early part of the fifteenth century that Palla degli Strozzi took steps to carry out the project that had been in the mind of Petrarch, the founding of a public library. It was largely by word of mouth, therefore, that this early knowledge had to be transmitted. Fortunately the presence of foreign students in Italy at this time made this transmission feasible. (If human nature was the same then as now, it is not impossible that the very opposition of the faculties to the works of Leonardo led the students to investigate [133]them the more zealously.) At Vicenza in 1209, for example, there were Bohemians, Poles, Frenchmen, Burgundians, Germans, and Spaniards, not to speak of representatives of divers towns of Italy; and what was true there was also true of other intellectual centers. The knowledge could not fail to spread, therefore, and as a matter of fact we find numerous bits of evidence that this was the case. Although the bankers of Florence were forbidden to use these numerals in 1299, and the statutes of the university of Padua required stationers to keep the price lists of books "non per cifras, sed per literas claros,"[538] the numerals really made much headway from about 1275 on.
It was, however, rather exceptional for the common people of Germany to use the Arabic numerals before the sixteenth century, a good witness to this fact being the popular almanacs. Calendars of 1457-1496[539] have generally the Roman numerals, while Köbel's calendar of 1518 gives the Arabic forms as subordinate to the Roman. In the register of the Kreuzschule at Dresden the Roman forms were used even until 1539.
While not minimizing the importance of the scientific work of Leonardo of Pisa, we may note that the more popular treatises by Alexander de Villa Dei (c. 1240 A.D.) and John of Halifax (Sacrobosco, c. 1250 A.D.) were much more widely used, and doubtless contributed more to the spread of the numerals among the common people.
The Carmen de Algorismo[540] of Alexander de Villa Dei was written in verse, as indeed were many other textbooks of that time. That it was widely used is evidenced by the large number of manuscripts[541] extant in European libraries. Sacrobosco's Algorismus,[542] in which some lines from the Carmen are quoted, enjoyed a wide popularity as a textbook for university instruction.[543] The work was evidently written with this end in view, as numerous commentaries by university lecturers are found. Probably the most widely used of these was that of Petrus de Dacia[544] written in 1291. These works throw an interesting light upon the method of instruction in mathematics in use in the universities from the thirteenth even to the sixteenth century. Evidently the text was first read and copied by students.[545] Following this came line by line an exposition of the text, such as is given in Petrus de Dacia's commentary.
Sacrobosco's work is of interest also because it was probably due to the extended use of this work that the [135]term Arabic numerals became common. In two places there is mention of the inventors of this system. In the introduction it is stated that this science of reckoning was due to a philosopher named Algus, whence the name algorismus,[546] and in the section on numeration reference is made to the Arabs as the inventors of this science.[547] While some of the commentators, Petrus de Dacia[548] among them, knew of the Hindu origin, most of them undoubtedly took the text as it stood; and so the Arabs were credited with the invention of the system.
The first definite trace that we have of an algorism in the French language is found in a manuscript written about 1275.[549] This interesting leaf, for the part on algorism consists of a single folio, was noticed by the Abbé Lebœuf as early as 1741,[550] and by Daunou in 1824.[551] It then seems to have been lost in the multitude of Paris manuscripts; for although Chasles[552] relates his vain search for it, it was not rediscovered until 1882. In that year M. Ch. Henry found it, and to his care we owe our knowledge of the interesting manuscript. The work is anonymous and is devoted almost entirely to geometry, only [136]two pages (one folio) relating to arithmetic. In these the forms of the numerals are given, and a very brief statement as to the operations, it being evident that the writer himself had only the slightest understanding of the subject.
Once the new system was known in France, even thus superficially, it would be passed across the Channel to England. Higden,[553] writing soon after the opening of the fourteenth century, speaks of the French influence at that time and for some generations preceding:[554] "For two hundred years children in scole, agenst the usage and manir of all other nations beeth compelled for to leave hire own language, and for to construe hir lessons and hire thynges in Frensche.... Gentilmen children beeth taught to speke Frensche from the tyme that they bith rokked in hir cradell; and uplondissche men will likne himself to gentylmen, and fondeth with greet besynesse for to speke Frensche."
The question is often asked, why did not these new numerals attract more immediate attention? Why did they have to wait until the sixteenth century to be generally used in business and in the schools? In reply it may be said that in their elementary work the schools always wait upon the demands of trade. That work which pretends to touch the life of the people must come reasonably near doing so. Now the computations of business until about 1500 did not demand the new figures, for two reasons: First, cheap paper was not known. Paper-making of any kind was not introduced into Europe until [137]the twelfth century, and cheap paper is a product of the nineteenth. Pencils, too, of the modern type, date only from the sixteenth century. In the second place, modern methods of operating, particularly of multiplying and dividing (operations of relatively greater importance when all measures were in compound numbers requiring reductions at every step), were not yet invented. The old plan required the erasing of figures after they had served their purpose, an operation very simple with counters, since they could be removed. The new plan did not as easily permit this. Hence we find the new numerals very tardily admitted to the counting-house, and not welcomed with any enthusiasm by teachers.[555]
Aside from their use in the early treatises on the new art of reckoning, the numerals appeared from time to time in the dating of manuscripts and upon monuments. The oldest definitely dated European document known [138]to contain the numerals is a Latin manuscript,[556] the Codex Vigilanus, written in the Albelda Cloister not far from Logroño in Spain, in 976 A.D. The nine characters (of ġobār type), without the zero, are given as an addition to the first chapters of the third book of the Origines by Isidorus of Seville, in which the Roman numerals are under discussion. Another Spanish copy of the same work, of 992 A.D., contains the numerals in the corresponding section. The writer ascribes an Indian origin to them in the following words: "Item de figuris arithmeticę. Scire debemus in Indos subtilissimum ingenium habere et ceteras gentes eis in arithmetica et geometria et ceteris liberalibus disciplinis concedere. Et hoc manifestum est in nobem figuris, quibus designant unumquemque gradum cuiuslibet gradus. Quarum hec sunt forma." The nine ġobār characters follow. Some of the abacus forms[557] previously given are doubtless also of the tenth century. The earliest Arabic documents containing the numerals are two manuscripts of 874 and 888 A.D.[558] They appear about a century later in a work[559] written at Shiraz in 970 A.D. There is also an early trace of their use on a pillar recently discovered in a church apparently destroyed as early as the tenth century, not far from the Jeremias Monastery, in Egypt. [139]A graffito in Arabic on this pillar has the date 349 A.H., which corresponds to 961 A.D.[560] For the dating of Latin documents the Arabic forms were used as early as the thirteenth century.[561]
On the early use of these numerals in Europe the only scientific study worthy the name is that made by Mr. G. F. Hill of the British Museum.[562] From his investigations it appears that the earliest occurrence of a date in these numerals on a coin is found in the reign of Roger of Sicily in 1138.[563] Until recently it was thought that the earliest such date was 1217 A.D. for an Arabic piece and 1388 for a Turkish one.[564] Most of the seals and medals containing dates that were at one time thought to be very early have been shown by Mr. Hill to be of relatively late workmanship. There are, however, in European manuscripts, numerous instances of the use of these numerals before the twelfth century. Besides the example in the Codex Vigilanus, another of the tenth century has been found in the St. Gall MS. now in the University Library at Zürich, the forms differing materially from those in the Spanish codex.
The third specimen in point of time in Mr. Hill's list is from a Vatican MS. of 1077. The fourth and fifth specimens are from the Erlangen MS. of Boethius, of the same [140](eleventh) century, and the sixth and seventh are also from an eleventh-century MS. of Boethius at Chartres. These and other early forms are given by Mr. Hill in this table, which is reproduced with his kind permission.
This is one of more than fifty tables given in Mr. Hill's valuable paper, and to this monograph students [141]are referred for details as to the development of number-forms in Europe from the tenth to the sixteenth century. It is of interest to add that he has found that among the earliest dates of European coins or medals in these numerals, after the Sicilian one already mentioned, are the following: Austria, 1484; Germany, 1489 (Cologne); Switzerland, 1424 (St. Gall); Netherlands, 1474; France, 1485; Italy, 1390.[565]
The earliest English coin dated in these numerals was struck in 1551,[566] although there is a Scotch piece of 1539.[567] In numbering pages of a printed book these numerals were first used in a work of Petrarch's published at Cologne in 1471.[568] The date is given in the following form in the Biblia Pauperum,[569] a block-book of 1470,
while in another block-book which possibly goes back to c. 1430[570] the numerals appear in several illustrations, with forms as follows:
Many printed works anterior to 1471 have pages or chapters numbered by
hand, but many of these numerals are [142]of date much later than
the printing of the work. Other works were probably numbered directly
after printing. Thus the chapters 2, 3, 4, 5, 6 in a book of 1470[571] are numbered as
follows: Capitulem  m.,...
m.,...  m.,... 4m.,... v,... vi, and
followed by Roman numerals. This appears in the body of the text, in
spaces left by the printer to be filled in by hand. Another book[572] of 1470 has pages
numbered by hand with a mixture of Roman and Hindu numerals, thus,
m.,... 4m.,... v,... vi, and
followed by Roman numerals. This appears in the body of the text, in
spaces left by the printer to be filled in by hand. Another book[572] of 1470 has pages
numbered by hand with a mixture of Roman and Hindu numerals, thus,
 | for 125 | 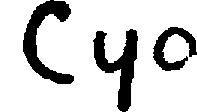 | for 150 |
 | for 147 |  | for 202 |
As to monumental inscriptions,[573] there was once thought to be a gravestone at Katharein, near Troppau, with the date 1007, and one at Biebrich of 1299. There is no doubt, however, of one at Pforzheim of 1371 and one at Ulm of 1388.[574] Certain numerals on Wells Cathedral have been assigned to the thirteenth century, but they are undoubtedly considerably later.[575]
The table on page 143 will serve to supplement that from Mr. Hill's work.[576]
 | ||
| a [577] | 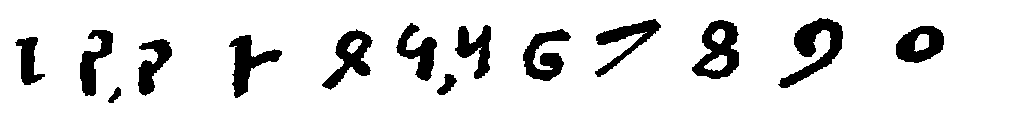 | Twelfth century A.D. |
| b [578] | 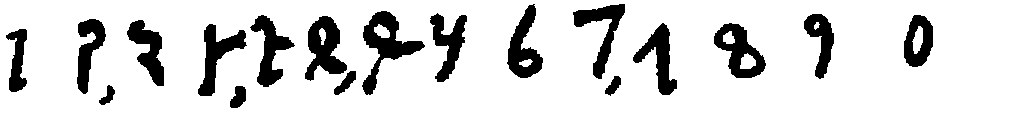 | 1197 A.D. |
| c [579] | 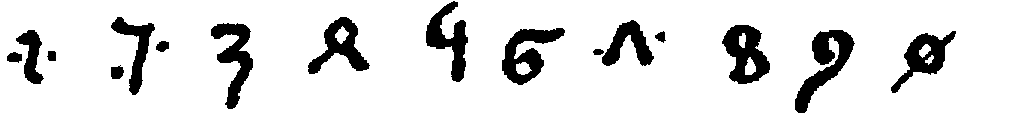 | 1275 A.D. |
| d [580] |  | c. 1294 A.D. |
| e [581] |  | c. 1303 A.D. |
| f [582] | 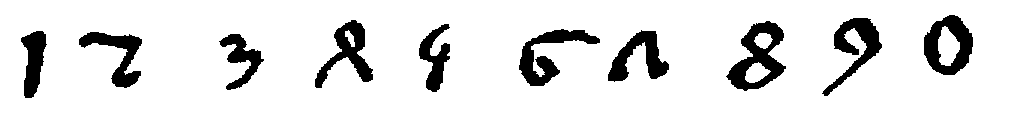 | c. 1360 A.D. |
| g [583] | 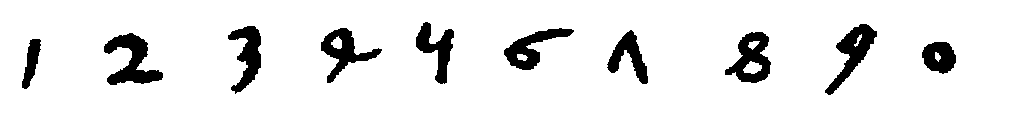 | c. 1442 A.D. |
For the sake of further comparison, three illustrations from works in Mr. Plimpton's library, reproduced from the Rara Arithmetica, may be considered. The first is from a Latin manuscript on arithmetic,[584] of which the original was written at Paris in 1424 by Rollandus, a Portuguese physician, who prepared the work at the command of John of Lancaster, Duke of Bedford, at one time Protector of England and Regent of France, to whom the work is dedicated. The figures show the successive powers of 2. The second illustration is from Luca da Firenze's Inprencipio darte dabacho,[585] c. 1475, and the third is from an anonymous manuscript[586] of about 1500.
As to the forms of the numerals, fashion played a leading part until printing was invented. This tended to fix these forms, although in writing there is still a great variation, as witness the French 5 and the German 7 and 9. Even in printing there is not complete uniformity, [145]and it is often difficult for a foreigner to distinguish between the 3 and 5 of the French types.
As to the particular numerals, the following are some of the forms to be found in the later manuscripts and in the early printed books.
1. In the early printed books "one" was often i, perhaps to save types, just as some modern typewriters use the same character for l and 1.[587] In the manuscripts the "one" appears in such forms as[588]
2. "Two" often appears as z in the early printed books, 12 appearing as iz.[589] In the medieval manuscripts the following forms are common:[590]
It is evident, from the early traces, that it is merely a cursive form
for the primitive 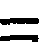 ,
just as 3 comes from
,
just as 3 comes from  , as
in the Nānā Ghāt inscriptions.
, as
in the Nānā Ghāt inscriptions.
3. "Three" usually had a special type in the first printed books,
although occasionally it appears as 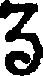 .[591] In the
medieval manuscripts it varied rather less than most of the others. The
following are common forms:[592]
.[591] In the
medieval manuscripts it varied rather less than most of the others. The
following are common forms:[592]
4. "Four" has changed greatly; and one of the first tests as to the
age of a manuscript on arithmetic, and the place where it was written, is
the examination of this numeral. Until the time of printing the most
common form was 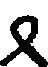 , although the
Florentine manuscript of Leonard of Pisa's work has the form
, although the
Florentine manuscript of Leonard of Pisa's work has the form 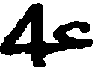 ;[593] but the manuscripts show that the
Florentine arithmeticians and astronomers rather early began to
straighten the first of these forms up to forms like
;[593] but the manuscripts show that the
Florentine arithmeticians and astronomers rather early began to
straighten the first of these forms up to forms like  [594] and
[594] and  [594] or
[594] or 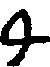 ,[595] more closely resembling our own. The
first printed books generally used our present form[596] with the closed top
,[595] more closely resembling our own. The
first printed books generally used our present form[596] with the closed top 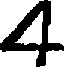 , the open top used in writing (
, the open top used in writing ( 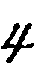 ) being [147]purely modern. The
following are other forms of the four, from various manuscripts:[597]
) being [147]purely modern. The
following are other forms of the four, from various manuscripts:[597]
5. "Five" also varied greatly before the time of printing. The following are some of the forms:[598]
6. "Six" has changed rather less than most of the others. The chief variation has been in the slope of the top, as will be seen in the following:[599]
7. "Seven," like "four," has assumed its present erect form only since the fifteenth century. In medieval times it appeared as follows:[600]
8. "Eight," like "six," has changed but little. In medieval times there are a few variants of interest as follows:[601]
In the sixteenth century, however, there was manifested a tendency to
write it  .[602]
.[602]
9. "Nine" has not varied as much as most of the others. Among the medieval forms are the following:[603]
0. The shape of the zero also had a varied history. The following are common medieval forms:[604]
The explanation of the place value was a serious matter to most of the early writers. If they had been using an abacus constructed like the Russian chotü, and had placed this before all learners of the positional system, there would have been little trouble. But the medieval [149]line-reckoning, where the lines stood for powers of 10 and the spaces for half of such powers, did not lend itself to this comparison. Accordingly we find such labored explanations as the following, from The Crafte of Nombrynge:
"Euery of these figuris bitokens hym selfe & no more, yf he stonde in the first place of the rewele....
"If it stonde in the secunde place of the rewle, he betokens ten tymes hym selfe, as this figure 2 here 20 tokens ten tyme hym selfe, that is twenty, for he hym selfe betokens tweyne, & ten tymes twene is twenty. And for he stondis on the lyft side & in the secunde place, he betokens ten tyme hym selfe. And so go forth....
"Nil cifra significat sed dat signare sequenti. Expone this verse. A cifre tokens noȝt, bot he makes the figure to betoken that comes after hym more than he shuld & he were away, as thus 10. here the figure of one tokens ten, & yf the cifre were away & no figure byfore hym he schuld token bot one, for than he schuld stonde in the first place...."[605]
It would seem that a system that was thus used for dating documents, coins, and monuments, would have been generally adopted much earlier than it was, particularly in those countries north of Italy where it did not come into general use until the sixteenth century. This, however, has been the fate of many inventions, as witness our neglect of logarithms and of contracted processes to-day.
As to Germany, the fifteenth century saw the rise of the new symbolism; the sixteenth century saw it slowly [150]gain the mastery; the seventeenth century saw it finally conquer the system that for two thousand years had dominated the arithmetic of business. Not a little of the success of the new plan was due to Luther's demand that all learning should go into the vernacular.[606]
During the transition period from the Roman to the Arabic numerals, various anomalous forms found place. For example, we have in the fourteenth century cα for 104;[607] 1000. 300. 80 et 4 for 1384;[608] and in a manuscript of the fifteenth century 12901 for 1291.[609] In the same century m. cccc. 8II appears for 1482,[610] while MoCCCCo50 (1450) and MCCCCXL6 (1446) are used by Theodoricus Ruffi about the same time.[611] To the next century belongs the form 1vojj for 1502. Even in Sfortunati's Nuovo lume[612] the use of ordinals is quite confused, the propositions on a single page being numbered "tertia," "4," and "V."
Although not connected with the Arabic numerals in any direct way, the medieval astrological numerals may here be mentioned. These are given by several early writers, but notably by Noviomagus (1539),[613] as follows[614]:
Thus we find the numerals gradually replacing the Roman forms all over Europe, from the time of Leonardo of Pisa until the seventeenth century. But in the Far East to-day they are quite unknown in many countries, and they still have their way to make. In many parts of India, among the common people of Japan and China, in Siam and generally about the Malay Peninsula, in Tibet, and among the East India islands, the natives still adhere to their own numeral forms. Only as Western civilization is making its way into the commercial life of the East do the numerals as used by us find place, save as the Sanskrit forms appear in parts of India. It is therefore with surprise that the student of mathematics comes to realize how modern are these forms so common in the West, how limited is their use even at the present time, and how slow the world has been and is in adopting such a simple device as the Hindu-Arabic numerals.
Transcriber's note: many of the entries refer to footnotes linked from the page numbers given.
Abbo of Fleury, 122
‛Abdallāh ibn al-Ḥasan, 92
‛Abdallatīf ibn Yūsuf, 93
‛Abdalqādir ibn ‛Alī al-Sakhāwī, 6
Abenragel, 34
Abraham ibn Meïr ibn Ezra, see Rabbi ben Ezra
Abū ‛Alī al-Ḥosein ibn Sīnā, 74
Abū 'l-Qāsim, 92
Abū 'l-Ṭeiyib, 97
Abū Naṣr, 92
Abū Roshd, 113
Abu Sahl Dunash ibn Tamim, 65, 67
Adelhard of Bath, 5, 55, 97, 119, 123, 126
Adhemar of Chabanois, 111
Aḥmed al-Nasawī, 98
Aḥmed ibn Moḥammed, 94
Aḥmed ibn ‛Omar, 93
Akṣaras, 32
Alanus ab Insulis, 124
Al-Baġdādī, 93
Al-Battānī, 54
Albelda (Albaida) MS., 116
Albert, J., 62
Albert of York, 103
Al-Bīrūnī, 6, 41, 49, 65, 92, 93
Alcuin, 103
Alexander the Great, 76
Alexander de Villa Dei, 11, 133
Al-Fazārī, 92
Alfred, 103
Algebra, etymology, 5
Algerian numerals, 68
Algorism, 97
Algorismus cifra, 120
Al-Ḥaṣṣār, 65
‛Alī ibn Abī Bekr, 6
Al-Karābīsī, 93
Al-Khowārazmī, 4, 9, 10, 92, 97, 98, 125, 126
Almagest, 54
Al-Maġrebī, 93
Al-Maḥallī, 6
Al-Nadīm, 9
Alphabetic numerals, 39, 40, 43
Al-Qāsim, 92
Al-Qass, 94
Al-Sakhāwī, 6
Al-Ṣardafī, 93
Al-Sijzī, 94
Ambrosoli, 118
Aṅkapalli, 43
Arbuthnot, 141
[154]Arcus Pictagore, 122
Arjuna, 15
Ars memorandi, 141
Aryan numerals, 19
Aschbach, 134
Ashmole, 134
Astrological numerals, 150
Augustus, 80
Averroës, 113
Babylonian numerals, 28
Babylonian zero, 51
Bacon, R., 131
Bakhṣālī manuscript, 43, 49, 52, 53
Ball, C. J., 35
Bāṇa, 44
Barth, A., 39
Bayang inscriptions, 39
Bayer, 33
Bayley, E. C., 19, 23, 30, 32, 52, 89
Beazley, 75
Bede, see Bæda
Beldomandi, 137
Beloch, J., 77
Benfey, T., 26
Besagne, 128
Besant, W., 109
Bettino, 36
Biernatzki, 32
Biot, 32
Blassière, 119
Bloomfield, 48
Blume, 85
Boeckh, 62
Boehmer, 143
Boeschenstein, 119
Boissière, 63
Bombelli, 81
Bonaini, 128
Boncompagni, 5, 6, 10, 48, 49, 123, 125
Borghi, 59
Borgo, 119
Bougie, 130
Bowring, J., 56
Brahmagupta, 52
Brandis, J., 54
Brockhaus, 43
Büdinger, 110
Bugia, 130
Bühler, G., 15, 19, 22, 31, 44, 49
Burgess, 25
Bürk, 13
Burmese numerals, 36
Buteo, 61
Caldwell, R., 19
Calendars, 133
Calmet, 34
[155]Capella, 86
Cappelli, 143
Cardan, 119
Casagrandi, 132
Cassiodorus, 72
Cataldi, 62
Cataneo, 3
Ceretti, 32
Ceylon numerals, 36
Chalfont, F. H., 28
Champenois, 60
Characters, see Caracteres
Charlemagne, 103
Chasles, 54, 60, 85, 116, 122, 135
Chassant, L. A., 142
Chaucer, 121
Chiffre, 58
Chinese zero, 56
Cipher, 58
Codex Vigilanus, 138
Codrington, O., 139
Coins dated, 141
Cosmas, 82
Cossali, 5
Counters, 117
Courteille, 8
Coxe, 59
Crafte of Nombrynge, 11, 87, 149
Crusades, 109
Cyfra, 55
Dagomari, 146
D'Alviella, 15
Dante, 72
Daunou, 135
Delambre, 54
Devanāgarī, 7
Devoulx, A., 68
Dhruva, 49
Dicæarchus of Messana, 77
Digits, 119
Diodorus Siculus, 76
Du Cange, 62
Dumesnil, 36
Dvivedī, 44
East and West, relations, 73-81, 100-109
Egyptian numerals, 27
Eisenlohr, 28
Elia Misrachi, 57
Enchiridion Algorismi, 58
Eneström, 5, 48, 59, 97, 125, 128
Europe, numerals in, 63, 99, 128, 136
Eusebius Caesariensis, 142
Euting, 21
Ewald, P., 116
Fibonacci, see Leonardo of Pisa
Figura nihili, 58
Figures, 119. See numerals.
Finaeus, 57
Firdusī, 81
Fitz Stephen, W., 109
[156]Florus, 80
Flügel, G., 68
Francisco de Retza, 142
François, 58
Friedlein, G., 84, 113, 116, 122
Froude, J. A., 129
Gandhāra, 19
Garbe, 48
Gasbarri, 58
Gerber, 113
Gerhardt, C. I., 43, 56, 93, 118
Gherard of Cremona, 125
Gibbon, 72
Giles, H. A., 79
Ginanni, 81
Giovanni di Danti, 58
Ġobār numerals, 65, 100, 112, 124, 138
Gow, J., 81
Grammateus, 61
Greek origin, 33
Green, J. R., 109
Guglielmini, 128
Gulistān, 102
Günther, S., 131
Guyard, S., 82
Hankel, 93
Havet, 110
Heath, T. L., 125
Hebrew numerals, 127
Hecatæus, 75
Heilbronner, 5
Henry, C., 5, 31, 55, 87, 120, 135
Heriger, 122
Hermannus Contractus, 123
Heyd, 75
Higden, 136
Hilprecht, H. V., 28
Hindu forms, early, 12
Hindu number names, 42
Hodder, 62
Holywood, see Sacrobosco
Hopkins, E. W., 12
Ḥosein ibn Moḥammed al-Maḥallī, 6
Hostus, M., 56
Howard, H. H., 29
Hrabanus Maurus, 72
Huart, 7
Huet, 33
Hugo, H., 57
Humboldt, A. von, 62
Huswirt, 58
Iamblichus, 81
Ibn Abī Ya‛qūb, 9
Ibn al-Adamī, 92
Ibn al-Bannā, 93
Ibn Wahab, 103
India, history of, 14
writing in, 18
Indicopleustes, 83
Indo-Bactrian numerals, 19
[157]Indrājī, 23
Isḥāq ibn Yūsuf al-Ṣardafī, 93
Jacob of Florence, 57
Jacquet, E., 38
Jamshid, 56
Jehan Certain, 59
Jevons, F. B., 76
Johannes Hispalensis, 48, 88, 124
John of Halifax, see Sacrobosco
John of Luna, see Johannes Hispalensis
Joseph Ispanus (Joseph Sapiens), 115
Justinian, 104
Kále, M. R., 26
Karabacek, 56
Karpinski, L. C., 126, 134, 138
Kātyāyana, 39
Kaye, C. R., 6, 16, 43, 46, 121
Keene, H. G., 15
Kern, 44
Kircher, A., 34
Kitāb al-Fihrist, see Fihrist
Kleinwächter, 32
Klos, 62
Krumbacher, K., 57
Kugler, F. X., 51
Lachmann, 85
Lami, G., 57
La Roche, 61
Lassen, 39
Lāṭyāyana, 39
Lebœuf, 135
Leonardo of Pisa, 5, 10, 57, 64, 74, 120, 128-133
Lethaby, W. R., 142
Levi, B., 13
Levias, 3
Light of Asia, 16
Luca da Firenze, 144
Lucas, 128
Mahābhārata, 18
Mahāvīrācārya, 53
Malabar numerals, 36
Malayalam numerals, 36
Mannert, 81
Margarita Philosophica, 146
Marie, 78
Marquardt, J., 85
Marshman, J. C., 17
Martin, T. H., 30, 62, 85, 113
Martines, D. C., 58
Māshāllāh, 3
Maspero, 28
Mauch, 142
Maximus Planudes, 2, 57, 66, 93, 120
Megasthenes, 77
Merchants, 114
Meynard, 8
Migne, 87
Mikami, Y., 56
Milanesi, 128
Moḥammed ibn ‛Abdallāh, 92
Moḥammed ibn Aḥmed, 6
Moḥammed ibn ‛Alī ‛Abdī, 8
Moḥammed ibn Mūsā, see Al-Khowārazmī
Molinier, 123
Monier-Williams, 17
[158]Morley, D., 126
Mortet, V., 11
Moseley, C. B., 33
Moṭahhar ibn Ṭāhir, 7
Mueller, A., 68
Mumford, J. K., 109
Muwaffaq al-Dīn, 93
Nabatean forms, 21
Nānā Ghāt inscriptions, 20, 22, 23, 40
Narducci, 123
Nasik cave inscriptions, 24
Naẓīf ibn Yumn, 94
Neander, A., 75
Neo-Pythagoreans, 64
Nesselmann, 58
Newman, Cardinal, 96
Newman, F. W., 131
Nöldeke, Th., 91
Notation, 61
Null, 61
Numerals,
Algerian, 68
astrological, 150
early ideas of origin, 1
Hindu, 26
Moroccan, 68
Nabatean, 21
supposed Arabic origin, 2
supposed Babylonian origin, 28
supposed Chaldean and Jewish origin, 3
supposed Chinese origin, 28, 32
supposed Egyptian origin, 27, 30, 69, 70
supposed Greek origin, 33
supposed Phœnician origin, 32
Pali, 22
Pañcasiddhāntikā, 44
Pātalīpuṭra, 77
Patna, 77
Patrick, R., 119
Payne, E. J., 106
Pegolotti, 107
Perrot, 80
Pertz, 115
Pez, P. B., 117
"Philalethes," 75
Phillips, G., 107
Picavet, 105
Pichler, F., 141
Pihan, A. P., 36
Pisa, 128
Planudes, see Maximus Planudes
Plimpton, G. A., 56, 59, 85, 143, 144, 145, 148
Pliny, 76
Polo, N. and M., 107
[159]Prändel, J. G., 54
Propertius, 80
Prosdocimo de' Beldomandi, 137
Prou, 143
Putnam, 103
Pythagoras, 63
Pythagorean numbers, 13
Pytheas of Massilia, 76
Radulph of Laon, 60, 113, 118, 124
Raets, 62
Rainer, see Gemma Frisius
Rāmāyana, 18
Raoul Glaber, 123
Rapson, 77
Rauhfuss, see Dasypodius
Raumer, K. von, 111
Reveillaud, 36
Riese, A., 119
Robertson, 81
Roediger, J., 68
Rollandus, 144
Romagnosi, 81
Rosen, F., 5
Rotula, 60
Rudolff, 85
Ruffi, 150
Sachau, 6
Sa‛dī, 102
Śaka inscriptions, 20
Samū'īl ibn Yaḥyā, 93
Śāradā characters, 55
Savonne, 60
Scaliger, J. C., 73
Scheubel, 62
Schlegel, 12
Schmidt, 133
Schroeder, L. von, 13
Scylax, 75
Shelley, W., 126
Siamese numerals, 36
Ṣifr, 57
Sigsboto, 55
Sihāb al-Dīn, 67
Silberberg, 60
Simon, 13
Sinān ibn al-Fatḥ, 93
Sindbad, 100
Sindhind, 97
Sipos, 60
Sirr, H. C., 75
Skeel, C. A., 74
Smith, D. E., 11, 17, 53, 86, 141, 143
Smith, Wm., 75
Smṛti, 17
Spitta-Bey, 5
Sprenger, 94
Śrautasūtra, 39
Steffens, F., 116
Steinschneider, 5, 57, 65, 66, 98, 126
Stifel, 62
[160]Subandhus, 44
Suetonius, 80
Suleimān, 100
Suter, 5, 9, 68, 69, 93, 116, 131
Sūtras, 13
Sykes, P. M., 75
Sylvester II, see Gerbert
Symonds, J. A., 129
Tennent, J. E., 75
Texada, 60
Theophanes, 64
Thibaut, G., 12, 13, 16, 44, 47
Tibetan numerals, 36
Timotheus, 103
Trenchant, 60
Trevisa, 136
Treviso arithmetic, 145
Trivium and quadrivium, 73
Tsin, 56
Tunis, 65
Turnour, G., 75
Valla, G., 61
Van der Schuere, 62
Vāsavadattā, 44
Vaux, W. S. W., 91
Vedāṅgas, 17
Vergil, 80
Vincent, A. J. H., 57
Vogt, 13
Voizot, P., 36
Wattenbach, 143
Weber, A., 31
Weidler, I. F. and G. I., 63, 66
Whitney, W. D., 13
Wilford, F., 75
Wilkens, 62
Wilkinson, J. G., 70
Willichius, 3
Woepcke, 3, 6, 42, 63, 64, 65, 67, 69, 70, 94, 113, 138
Wolack, G., 54
Woodruff, C. E., 32
Word and letter numerals, 38, 44
Wüstenfeld, 74
Yule, H., 107
REVISED EDITION
12mo. Half morocco. 530 pages. List price, $1.50; mailing price, $1.65
This book is a thorough revision of the author's "College Algebra." Some chapters of the old edition have been wholly rewritten, and the other chapters have been rewritten in part and greatly improved. The order of topics has been changed to a certain extent; the plan is to have each chapter as complete in itself as possible, so that the teacher may vary the order of succession at his discretion.
As the name implies, the work is intended for colleges and scientific schools. The first part is simply a review of the principles of algebra preceding Quadratic Equations, with just enough examples to illustrate and enforce these principles. By this brief treatment of the first chapters sufficient space is allowed, without making the book cumbersome, for a full discussion of Quadratic Equations, The Binomial Theorem, Choice Chance, Series, Determinants, and the General Properties of Equations.
Every effort has been made to present in the clearest light each subject discussed, and to give in matter and methods the best training in algebraic analysis at present attainable.
ADDITIONAL PUBLICATIONS
By G. A. WENTWORTH
| List price | Mailing price | |
| Plane and Solid Geometry (Revised Edition) | $1.25 | $1.40 |
| Plane Geometry (Revised Edition) | .75 | .85 |
| Solid Geometry (Revised Edition) | .75 | .85 |
| Analytic Geometry | 1.25 | 1.35 |
| Trigonometries (Second Revised Editions) |
A list of the various editions of Wentworth's Trigonometries will be sent on request.
By DAVID EUGENE SMITH,
Professor of Mathematics in Teachers College, Columbia University
12mo, cloth, 154 pages, 50 cents
This work is intended to serve as an introduction to the study of algebra, and is adapted to the needs of the seventh or eighth school year. It is arranged in harmony with the leading courses of study that include algebra in the curriculum of the grades.
The relation of algebra to arithmetic is emphasized, the subject is treated topically, and each important point is touched at least twice. The book begins by showing the uses of algebra, employing such practical applications as are within the pupil's range of knowledge. When an interest has thus been awakened in the subject, the fundamental operations are presented with the simple explanations necessary to make the student independent of dogmatic rules. Throughout the book abundant oral and written drill exercises are provided. The work includes linear equations with two unknown quantities, and easy quadratics.
The leading features may be summarized as follows: (1) an arrangement in harmony with existing courses of study; (2) a presentation designed to awaken the interest of the pupils; (3) a topical arrangement for each half year, every important topic being repeated; (4) simplicity of explanations; (5) development of the relation of algebra to arithmetic both in theory and in applications; (6) emphasis laid on the importance of oral as well as written algebra.
| List price | |
| Allen: Civics and Health | $1.25 |
| Brigham: Geographic Influences in American History | 1.25 |
| Channing and Hart: Guide to the Study of American History | 2.00 |
| Hall: Aspects of Child Life and Education | 1.50 |
| Hodge: Nature Study and Life | 1.50 |
| Johnson: Education by Plays and Games | .90 |
| Johnson: What to Do at Recess | .25 |
| Kern: Among Country Schools | 1.25 |
| Mace: Method in History | 1.00 |
| MacVicar: The Principles of Education | .60 |
| Moral Training in the Public Schools | 1.25 |
| Prince: Courses of Studies and Methods of Teaching | .75 |
| Scott: Social Education | 1.25 |
| Tompkins: Philosophy of School Management | .75 |
| Tompkins: Philosophy of Teaching | .75 |
| Wiltse: Place of the Story in Early Education, and Other Essays. A Manual for Teachers | .50 |
| Comings: Complete Record—Attendance and Scholarship | |
| Graded-School Edition | .30 |
| High-School Edition | .30 |
| Ginn and Company: Teacher's Class Books | |
| No. I | .30 |
| No. II | .40 |
| Twenty Weeks' Class Book | .30 |
FOR HIGHER SCHOOLS AND COLLEGES
| List price | |
| Bailey and Woods: Analytic Geometry | $2.00 |
| Beman and Smith: Academic Algebra | 1.12 |
| Beman and Smith: Higher Arithmetic | .80 |
| Beman and Smith: New Plane and Solid Geometry | 1.25 |
| Breckenridge, Mersereau, and Moore: Shop Problems in Mathematics | 1.00 |
| Byerly: Differential Calculus | 2.00 |
| Byerly: Integral Calculus (Second Edition. Revised and Enlarged) | 2.00 |
| Eisenhart: Differential Geometry of Curves and Surfaces | 4.50 |
| Faunce: Descriptive Geometry | 1.25 |
| Fine: College Algebra | 1.50 |
| Granville: Plane and Spherical Trigonometry and Tables | 1.25 |
| Granville: Plane and Spherical Trigonometry Without Tables | 1.00 |
| Granville: Plane Trigonometry and Tables | 1.00 |
| Granville: Logarithmic Tables | .50 |
| Granville and Smith: Elements of Differential and Integral Calculus | 2.50 |
| Hardy: Analytic Geometry | 1.50 |
| Hardy: Elements of the Calculus | 1.50 |
| Hawkes: Advanced Algebra | 1.40 |
| Hawkes, Luby, and Touton: First Course in Algebra | 1.00 |
| Hedrick: Goursat's Mathematical Analysis. Vol. I | 4.00 |
| Hedrick and Kellogg: Applications of the Calculus to Mechanics | 1.25 |
| Hooper and Wells: Electrical Problems | 1.25 |
| Lester: Integrals of Mechanics | .80 |
| Peirce, B. O.: Newtonian Potential Function (Third, Revised, and Enlarged Edition) | 2.50 |
| Peirce, J. M.: Elements of Logarithms | .50 |
| Peirce, J. M.: Mathematical Tables | .40 |
| Pierpont: Theory of Functions of Real Variables. Vol. I | 4.50 |
| Shepard: Problems in the Strength of Materials | 1.25 |
| Slocum and Hancock: Textbook on the Strength of Materials | 3.00 |
| Smith and Gale: Elements of Analytic Geometry | 2.00 |
| Smith and Gale: Introduction to Analytic Geometry | 1.25 |
| Smith and Longley: Theoretical Mechanics | 2.50 |
| Taylor: Elements of the Calculus (Revised and Enlarged Edition) | 2.00 |
| Taylor: Plane and Spherical Trigonometry | 1.00 |
| Taylor: Plane Trigonometry | .75 |
| Taylor and Puryear: Elements of Plane and Spherical Trigonometry | 1.25 |
| Wentworth: Advanced Arithmetic | 1.00 |
| Wentworth: Analytic Geometry | 1.25 |
| Wentworth: College Algebra (Revised Edition) | 1.50 |
| Wentworth: Elementary Algebra | 1.12 |
| Wentworth: Higher Algebra | 1.40 |
| Wentworth: New School Algebra | 1.12 |
| Wentworth: Plane and Solid Geometry (Revised Edition) | 1.25 |
| Wentworth: Plane Geometry (Revised Edition); Solid Geometry (Revised Edition), each | .75 |
| Wentworth: Trigonometries (Second Revised Editions) | |
| (For list, see Descriptive Catalogue) | |
| Woods and Bailey: A Course In Mathematics | |
| Volume I | 2.25 |
| Volume II | 2.25 |
[1] "Discipulus. Quis primus invenit numerum apud Hebræos et Ægyptios? Magister. Abraham primus invenit numerum apud Hebræos, deinde Moses; et Abraham tradidit istam scientiam numeri ad Ægyptios, et docuit eos: deinde Josephus." [Bede, De computo dialogus (doubtfully assigned to him), Opera omnia, Paris, 1862, Vol. I, p. 650.]
"Alii referunt ad Phœnices inventores arithmeticæ, propter eandem commerciorum caussam: Alii ad Indos: Ioannes de Sacrobosco, cujus sepulchrum est Lutetiæ in comitio Maturinensi, refert ad Arabes." [Ramus, Arithmeticæ libri dvo, Basel, 1569, p. 112.]
Similar notes are given by Peletarius in his commentary on the arithmetic of Gemma Frisius (1563 ed., fol. 77), and in his own work (1570 Lyons ed., p. 14): "La valeur des Figures commence au coste dextre tirant vers le coste senestre: au rebours de notre maniere d'escrire par ce que la premiere prattique est venue des Chaldees: ou des Pheniciens, qui ont été les premiers traffiquers de marchandise."
[2] Maximus Planudes (c. 1330) states that "the nine symbols come from the Indians." [Wäschke's German translation, Halle, 1878, p. 3.] Willichius speaks of the "Zyphræ Indicæ," in his Arithmeticæ libri tres (Strasburg, 1540, p. 93), and Cataneo of "le noue figure de gli Indi," in his Le pratiche delle dve prime mathematiche (Venice, 1546, fol. 1). Woepcke is not correct, therefore, in saying ("Mémoire sur la propagation des chiffres indiens," hereafter referred to as Propagation [Journal Asiatique, Vol. I (6), 1863, p. 34]) that Wallis (A Treatise on Algebra, both historical and practical, London, 1685, p. 13, and De algebra tractatus, Latin edition in his Opera omnia, 1693, Vol. II, p. 10) was one of the first to give the Hindu origin.
[3] From the 1558 edition of The Grovnd of Artes, fol. C, 5. Similarly Bishop Tonstall writes: "Qui a Chaldeis primum in finitimos, deinde in omnes pene gentes fluxit.... Numerandi artem a Chaldeis esse profectam: qui dum scribunt, a dextra incipiunt, et in leuam progrediuntur." [De arte supputandi, London, 1522, fol. B, 3.] Gemma Frisius, the great continental rival of Recorde, had the same idea: "Primùm autem appellamus dexterum locum, eo quòd haec ars vel à Chaldæis, vel ab Hebræis ortum habere credatur, qui etiam eo ordine scribunt"; but this refers more evidently to the Arabic numerals. [Arithmeticæ practicæ methodvs facilis, Antwerp, 1540, fol. 4 of the 1563 ed.] Sacrobosco (c. 1225) mentions the same thing. Even the modern Jewish writers claim that one of their scholars, Māshāllāh (c. 800), introduced them to the Mohammedan world. [C. Levias, The Jewish Encyclopedia, New York, 1905, Vol. IX, p. 348.]
[4] "... & que esto fu trouato di fare da gli Arabi con diece figure." [La prima parte del general trattato di nvmeri, et misvre, Venice, 1556, fol. 9 of the 1592 edition.]
[5] "Vom welchen Arabischen auch disz Kunst entsprungen ist." [Ain nerv geordnet Rechenbiechlin, Augsburg, 1514, fol. 13 of the 1531 edition. The printer used the letters rv for w in "new" in the first edition, as he had no w of the proper font.]
[6] Among them Glareanus: "Characteres simplices sunt nouem significatiui, ab Indis usque, siue Chaldæis asciti .1.2.3.4.5.6.7.8.9. Est item unus .0 circulus, qui nihil significat." [De VI. Arithmeticae practicae speciebvs, Paris, 1539, fol. 9 of the 1543 edition.]
[7] "Barbarische oder gemeine Ziffern." [Anonymous, Das Einmahl Eins cum notis variorum, Dresden, 1703, p. 3.] So Vossius (De universae matheseos natura et constitutione liber, Amsterdam, 1650, p. 34) calls them "Barbaras numeri notas." The word at that time was possibly synonymous with Arabic.
[8] His full name was ‛Abū ‛Abdallāh Moḥammed ibn Mūsā al-Khowārazmī. He was born in Khowārezm, "the lowlands," the country about the present Khiva and bordering on the Oxus, and lived at Bagdad under the caliph al-Māmūn. He died probably between 220 and 230 of the Mohammedan era, that is, between 835 and 845 A.D., although some put the date as early as 812. The best account of this great scholar may be found in an article by C. Nallino, "Al-Ḫuwārizmī" in the Atti della R. Accad. dei Lincei, Rome, 1896. See also Verhandlungen des 5. Congresses der Orientalisten, Berlin, 1882, Vol. II, p. 19; W. Spitta-Bey in the Zeitschrift der deutschen Morgenländ. Gesellschaft, Vol. XXXIII, p. 224; Steinschneider in the Zeitschrift der deutschen Morgenländ. Gesellschaft, Vol. L, p. 214; Treutlein in the Abhandlungen zur Geschichte der Mathematik, Vol. I, p. 5; Suter, "Die Mathematiker und Astronomen der Araber und ihre Werke," Abhandlungen zur Geschichte der Mathematik, Vol. X, Leipzig, 1900, p. 10, and "Nachträge," in Vol. XIV, p. 158; Cantor, Geschichte der Mathematik, Vol. I, 3d ed., pp. 712-733 etc.; F. Woepcke in Propagation, p. 489. So recently has he become known that Heilbronner, writing in 1742, merely mentions him as "Ben-Musa, inter Arabes celebris Geometra, scripsit de figuris planis & sphericis." [Historia matheseos universæ, Leipzig, 1742, p. 438.]
In this work most of the Arabic names will be transliterated substantially as laid down by Suter in his work Die Mathematiker etc., except where this violates English pronunciation. The scheme of pronunciation of oriental names is set forth in the preface.
[9] Our word algebra is from the title of one of his works, Al-jabr wa'l-muqābalah, Completion and Comparison. The work was translated into English by F. Rosen, London, 1831, and treated in L'Algèbre d'al-Khārizmi et les méthodes indienne et grecque, Léon Rodet, Paris, 1878, extract from the Journal Asiatique. For the derivation of the word algebra, see Cossali, Scritti Inediti, pp. 381-383, Rome, 1857; Leonardo's Liber Abbaci (1202), p. 410, Rome, 1857; both published by B. Boncompagni. "Almuchabala" also was used as a name for algebra.
[10] This learned scholar, teacher of O'Creat who wrote the Helceph ("Prologus N. Ocreati in Helceph ad Adelardum Batensem magistrum suum"), studied in Toledo, learned Arabic, traveled as far east as Egypt, and brought from the Levant numerous manuscripts for study and translation. See Henry in the Abhandlungen zur Geschichte der Mathematik, Vol. III, p. 131; Woepcke in Propagation, p. 518.
[11] The title is Algoritmi de numero Indorum. That he did not make this translation is asserted by Eneström in the Bibliotheca Mathematica, Vol. I (3), p. 520.
[12] Thus he speaks "de numero indorum per .IX. literas," and proceeds: "Dixit algoritmi: Cum uidissem yndos constituisse .IX. literas in uniuerso numero suo, propter dispositionem suam quam posuerunt, uolui patefacere de opera quod fit per eas aliquid quod esset leuius discentibus, si deus uoluerit." [Boncompagni, Trattati d'Aritmetica, Rome, 1857.] Discussed by F. Woepcke, Sur l'introduction de l'arithmétique indienne en Occident, Rome, 1859.
[13] Thus in a commentary by ‛Alī ibn Abī Bekr ibn al-Jamāl al-Anṣārī al-Mekkī on a treatise on ġobār arithmetic (explained later) called Al-murshidah, found by Woepcke in Paris (Propagation, p. 66), there is mentioned the fact that there are "nine Indian figures" and "a second kind of Indian figures ... although these are the figures of the ġobār writing." So in a commentary by Ḥosein ibn Moḥammed al-Maḥallī (died in 1756) on the Mokhtaṣar fī‛ilm el-ḥisāb (Extract from Arithmetic) by ‛Abdalqādir ibn ‛Alī al-Sakhāwī (died c. 1000) it is related that "the preface treats of the forms of the figures of Hindu signs, such as were established by the Hindu nation." [Woepcke, Propagation, p. 63.]
[14] See also Woepcke, Propagation, p. 505. The origin is discussed at much length by G. R. Kaye, "Notes on Indian Mathematics.—Arithmetical Notation," Journ. and Proc. of the Asiatic Soc. of Bengal, Vol. III, 1907, p. 489.
[15] Alberuni's India, Arabic version, London, 1887; English translation, ibid., 1888.
[16] Chronology of Ancient Nations, London, 1879. Arabic and English versions, by C. E. Sachau.
[17] India, Vol. I, chap. xvi.
[18] The Hindu name for the symbols of the decimal place system.
[19] Sachau's English edition of the Chronology, p. 64.
[20] Littérature arabe, Cl. Huart, Paris, 1902.
[21] Huart, History of Arabic Literature, English ed., New York, 1903, p. 182 seq.
[22] Al-Mas‛ūdī's Meadows of Gold, translated in part by Aloys Sprenger, London, 1841; Les prairies d'or, trad. par C. Barbier de Meynard et Pavet de Courteille, Vols. I to IX, Paris, 1861-1877.
[23] Les prairies d'or, Vol. VIII, p. 289 seq.
[24] Essays, Vol. II, p. 428.
[25] Loc. cit., p. 504.
[26] Matériaux pour servir à l'histoire comparée des sciences mathématiques chez les Grecs et les Orientaux, 2 vols., Paris, 1845-1849, pp. 438-439.
[27] He made an exception, however, in favor of the numerals, loc. cit., Vol. II, p. 503.
[28] Bibliotheca Arabico-Hispana Escurialensis, Madrid, 1760-1770, pp. 426-427.
[29] The author, Ibn al-Qifṭī, flourished A.D. 1198 [Colebrooke, loc. cit., note Vol. II, p. 510].
[30] "Liber Artis Logisticae à Mohamado Ben Musa Alkhuarezmita exornatus, qui ceteros omnes brevitate methodi ac facilitate praestat, Indorum que in praeclarissimis inventis ingenium & acumen ostendit." [Casiri, loc. cit., p. 427.]
[31] Maçoudi, Le livre de l'avertissement et de la révision. Translation by B. Carra de Vaux, Paris, 1896.
[32] Verifying the hypothesis of Woepcke, Propagation, that the Sindhind included a treatment of arithmetic.
[33] Aḥmed ibn ‛Abdallāh, Suter, Die Mathematiker, etc., p. 12.
[34] India, Vol. II, p. 15.
[35] See H. Suter, "Das Mathematiker-Verzeichniss im Fihrist," Abhandlungen zur Geschichte der Mathematik, Vol. VI, Leipzig, 1892. For further references to early Arabic writers the reader is referred to H. Suter, Die Mathematiker und Astronomen der Araber und ihre Werke. Also "Nachträge und Berichtigungen" to the same (Abhandlungen, Vol. XIV, 1902, pp. 155-186).
[36] Suter, loc. cit., note 165, pp. 62-63.
[37] "Send Ben Ali,... tùm arithmetica scripta maximè celebrata, quae publici juris fecit." [Loc. cit., p. 440.]
[38] Scritti di Leonardo Pisano, Vol. I, Liber Abbaci (1857); Vol. II, Scritti (1862); published by Baldassarre Boncompagni, Rome. Also Tre Scritti Inediti, and Intorno ad Opere di Leonardo Pisano, Rome, 1854.
[39] "Ubi ex mirabili magisterio in arte per novem figuras indorum introductus" etc. In another place, as a heading to a separate division, he writes, "De cognitione novem figurarum yndorum" etc. "Novem figure indorum he sunt 9 8 7 6 5 4 3 2 1."
[40] See An Ancient English Algorism, by David Eugene Smith, in Festschrift Moritz Cantor, Leipzig, 1909. See also Victor Mortet, "Le plus ancien traité francais d'algorisme," Bibliotheca Mathematica, Vol. IX (3), pp. 55-64.
[41] These are the two opening lines of the Carmen de Algorismo that the anonymous author is explaining. They should read as follows:
Haec algorismus ars praesens dicitur, in qua
Talibus Indorum fruimur bis quinque figuris.
What follows is the translation.
[42] Thibaut, Astronomie, Astrologie und Mathematik, Strassburg, 1899.
[43] Gustave Schlegel, Uranographie chinoise ou preuves directes que l'astronomie primitive est originaire de la Chine, et qu'elle a été empruntée par les anciens peuples occidentaux à la sphère chinoise; ouvrage accompagné d'un atlas céleste chinois et grec, The Hague and Leyden, 1875.
[44] E. W. Hopkins, The Religions of India, Boston, 1898, p. 7.
[45] R. C. Dutt, History of India, London, 1906.
[46] W. D. Whitney, Sanskrit Grammar, 3d ed., Leipzig, 1896.
[47] "Das Āpastamba-Śulba-Sūtra," Zeitschrift der deutschen Morgenländischen Gesellschaft, Vol. LV, p. 543, and Vol. LVI, p. 327.
[48] Geschichte der Math., Vol. I, 2d ed., p. 595.
[49] L. von Schroeder, Pythagoras und die Inder, Leipzig, 1884; H. Vogt, "Haben die alten Inder den Pythagoreischen Lehrsatz und das Irrationale gekannt?" Bibliotheca Mathematica, Vol. VII (3), pp. 6-20; A. Bürk, loc. cit.; Max Simon, Geschichte der Mathematik im Altertum, Berlin, 1909, pp. 137-165; three Sūtras are translated in part by Thibaut, Journal of the Asiatic Society of Bengal, 1875, and one appeared in The Pandit, 1875; Beppo Levi, "Osservazioni e congetture sopra la geometria degli indiani," Bibliotheca Mathematica, Vol. IX (3), 1908, pp. 97-105.
[50] Loc. cit.; also Indiens Literatur und Cultur, Leipzig, 1887.
[51] It is generally agreed that the name of the river Sindhu, corrupted by western peoples to Hindhu, Indos, Indus, is the root of Hindustan and of India. Reclus, Asia, English ed., Vol. III, p. 14.
[52] See the comments of Oppert, On the Original Inhabitants of Bharatavarṣa or India, London, 1893, p. 1.
[53] A. Hillebrandt, Alt-Indien, Breslau, 1899, p. 111. Fragmentary records relate that Khāravela, king of Kaliṅga, learned as a boy lekhā (writing), gaṇanā (reckoning), and rūpa (arithmetic applied to monetary affairs and mensuration), probably in the 5th century B.C. [Bühler, Indische Palaeographie, Strassburg, 1896, p. 5.]
[54] R. C. Dutt, A History of Civilization in Ancient India, London, 1893, Vol. I, p. 174.
[55] The Buddha. The date of his birth is uncertain. Sir Edwin Arnold put it c. 620 B.C.
[56] I.e. 100·107.
[57] There is some uncertainty about this limit.
[58] This problem deserves more study than has yet been given it. A beginning may be made with Comte Goblet d'Alviella, Ce que l'Inde doit à la Grèce, Paris, 1897, and H. G. Keene's review, "The Greeks in India," in the Calcutta Review, Vol. CXIV, 1902, p. 1. See also F. Woepeke, Propagation, p. 253; G. R. Kaye, loc. cit., p. 475 seq., and "The Source of Hindu Mathematics," Journal of the Royal Asiatic Society, July, 1910, pp. 749-760; G. Thibaut, Astronomie, Astrologie und Mathematik, pp. 43-50 and 76-79. It will be discussed more fully in Chapter VI.
[59] I.e. to 100,000. The lakh is still the common large unit in India, like the myriad in ancient Greece and the million in the West.
[60] This again suggests the Psammites, or De harenae numero as it is called in the 1544 edition of the Opera of Archimedes, a work in which the great Syracusan proposes to show to the king "by geometric proofs which you can follow, that the numbers which have been named by us ... are sufficient to exceed not only the number of a sand-heap as large as the whole earth, but one as large as the universe." For a list of early editions of this work see D. E. Smith, Rara Arithmetica, Boston, 1909, p. 227.
[61] I.e. the Wise.
[62] Sir Monier Monier-Williams, Indian Wisdom, 4th ed., London, 1893, pp. 144, 177. See also J. C. Marshman, Abridgment of the History of India, London, 1893, p. 2.
[63] For a list and for some description of these works see R. C. Dutt, A History of Civilization in Ancient India, Vol. II, p. 121.
[64] Professor Ramkrishna Gopal Bhandarkar fixes the date as the fifth century B.C. ["Consideration of the Date of the Mahābhārata," in the Journal of the Bombay Branch of the R. A. Soc., Bombay, 1873, Vol. X, p. 2.].
[65] Marshman, loc. cit., p. 2.
[66] A. C. Burnell, South Indian Palæography, 2d ed., London, 1878, p. 1, seq.
[67] This extensive subject of palpable arithmetic, essentially the history of the abacus, deserves to be treated in a work by itself.
[68] The following are the leading sources of information upon this subject: G. Bühler, Indische Palaeographie, particularly chap. vi; A. C. Burnell, South Indian Palæography, 2d ed., London, 1878, where tables of the various Indian numerals are given in Plate XXIII; E. C. Bayley, "On the Genealogy of Modern Numerals," Journal of the Royal Asiatic Society, Vol. XIV, part 3, and Vol. XV, part 1, and reprint, London, 1882; I. Taylor, in The Academy, January 28, 1882, with a repetition of his argument in his work The Alphabet, London, 1883, Vol. II, p. 265, based on Bayley; G. R. Kaye, loc. cit., in some respects one of the most critical articles thus far published; J. C. Fleet, Corpus inscriptionum Indicarum, London, 1888, Vol. III, with facsimiles of many Indian inscriptions, and Indian Epigraphy, Oxford, 1907, reprinted from the Imperial Gazetteer of India, Vol. II, pp. 1-88, 1907; G. Thibaut, loc. cit., Astronomie etc.; R. Caldwell, Comparative Grammar of the Dravidian Languages, London, 1856, p. 262 seq.; and Epigraphia Indica (official publication of the government of India), Vols. I-IX. Another work of Bühler's, On the Origin of the Indian Brāhma Alphabet, is also of value.
[69] The earliest work on the subject was by James Prinsep, "On the Inscriptions of Piyadasi or Aśoka," etc., Journal of the Asiatic Society of Bengal, 1838, following a preliminary suggestion in the same journal in 1837. See also "Aśoka Notes," by V. A. Smith, The Indian Antiquary, Vol. XXXVII, 1908, p. 24 seq., Vol. XXXVIII, pp. 151-159, June, 1909; The Early History of India, 2d ed., Oxford, 1908, p. 154; J. F. Fleet, "The Last Words of Aśoka," Journal of the Royal Asiatic Society, October, 1909, pp. 981-1016; E. Senart, Les inscriptions de Piyadasi, 2 vols., Paris, 1887.
[70] For a discussion of the minor details of this system, see Bühler, loc. cit., p. 73.
[71] Julius Euting, Nabatäische Inschriften aus Arabien, Berlin, 1885, pp. 96-97, with a table of numerals.
[72] For the five principal theories see Bühler, loc. cit., p. 10.
[73] Bayley, loc. cit., reprint p. 3.
[74] Bühler, loc. cit.; Epigraphia Indica, Vol. III, p. 134; Indian Antiquary, Vol. VI, p. 155 seq., and Vol. X, p. 107.
[75] Pandit Bhagavānlāl Indrājī, "On Ancient Nāgāri Numeration; from an Inscription at Nāneghāt," Journal of the Bombay Branch of the Royal Asiatic Society, 1876, Vol. XII, p. 404.
[76] Ib., p. 405. He gives also a plate and an interpretation of each numeral.
[77] These may be compared with Bühler's drawings, loc. cit.; with Bayley, loc. cit., p. 337 and plates; and with Bayley's article in the Encyclopædia Britannica, 9th ed., art. "Numerals."
[78] E. Senart, "The Inscriptions in the Caves at Nasik," Epigraphia Indica, Vol. VIII, pp. 59-96; "The Inscriptions in the Cave at Karle," Epigraphia Indica, Vol. VII, pp. 47-74; Bühler, Palaeographie, Tafel IX.
[79] See Fleet, loc. cit. See also T. Benfey, Sanskrit Grammar, London, 1863, p. 217; M. R. Kále, Higher Sanskrit Grammar, 2d ed., Bombay, 1898, p. 110, and other authorities as cited.
[80] Kharoṣṭhī numerals, Aśoka inscriptions, c. 250 B.C. Senart, Notes d'épigraphie indienne. Given by Bühler, loc. cit., Tafel I.
[81] Same, Śaka inscriptions, probably of the first century B.C. Senart, loc. cit.; Bühler, loc. cit.
[82] Brāhmī numerals, Aśoka inscriptions, c. 250 B.C. Indian Antiquary, Vol. VI, p. 155 seq.
[83] Same, Nānā Ghāt inscriptions, c. 150 B.C. Bhagavānlāl Indrājī, On Ancient Nāgarī Numeration, loc. cit. Copied from a squeeze of the original.
[84] Same, Nasik inscription, c. 100 B.C. Burgess, Archeological Survey Report, Western India; Senart, Epigraphia Indica, Vol. VII, pp. 47-79, and Vol. VIII, pp. 59-96.
[85] Kṣatrapa coins, c. 200 A.D. Journal of the Royal Asiatic Society, 1890, p. 639.
[86] Kuṣana inscriptions, c. 150 A.D. Epigraphia Indica, Vol. I, p. 381, and Vol. II, p. 201.
[87] Gupta Inscriptions, c. 300 A.D. to 450 A.D. Fleet, loc. cit., Vol. III.
[88] Valhabī, c. 600 A.D. Corpus, Vol. III.
[89] Bendall's Table of Numerals, in Cat. Sansk. Budd. MSS., British Museum.
[90] Indian Antiquary, Vol. XIII, 120; Epigraphia Indica, Vol. III, 127 ff.
[91] Fleet, loc. cit.
[92] Bayley, loc. cit., p. 335.
[93] From a copper plate of 493 A.D., found at Kārītalāī, Central India. [Fleet, loc. cit., Plate XVI.] It should be stated, however, that many of these copper plates, being deeds of property, have forged dates so as to give the appearance of antiquity of title. On the other hand, as Colebrooke long ago pointed out, a successful forgery has to imitate the writing of the period in question, so that it becomes evidence well worth considering, as shown in Chapter III.
[94] From a copper plate of 510 A.D., found at Majhgawāin, Central India. [Fleet, loc. cit., Plate XIV.]
[95] From an inscription of 588 A.D., found at Bōdh-Gayā, Bengal Presidency. [Fleet, loc. cit., Plate XXIV.]
[96] From a copper plate of 571 A.D., found at Māliyā, Bombay Presidency. [Fleet, loc. cit., Plate XXIV.]
[97] From a Bijayagaḍh pillar inscription of 372 A.D. [Fleet, loc. cit., Plate XXXVI, C.]
[98] From a copper plate of 434 A.D. [Indian Antiquary, Vol. I, p. 60.]
[99] Gadhwa inscription, c. 417 A.D. [Fleet, loc. cit., Plate IV, D.]
[100] Kārītalāī plate of 493 A.D., referred to above.
[101] It seems evident that the
Chinese four, curiously enough called "eight in the mouth," is only a
cursive 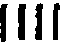 .
.
[102] Chalfont, F. H., Memoirs of the Carnegie Museum, Vol. IV, no. 1; J. Hager, An Explanation of the Elementary Characters of the Chinese, London, 1801.
[103] H. V. Hilprecht, Mathematical, Metrological and Chronological Tablets from the Temple Library at Nippur, Vol. XX, part I, of Series A, Cuneiform Texts Published by the Babylonian Expedition of the University of Pennsylvania, 1906; A. Eisenlohr, Ein altbabylonischer Felderplan, Leipzig, 1906; Maspero, Dawn of Civilization, p. 773.
[104] Sir H. H. Howard, "On the Earliest Inscriptions from Chaldea," Proceedings of the Society of Biblical Archæology, XXI, p. 301, London, 1899.
[105] For a bibliography of the principal hypotheses of this nature see Bühler, loc. cit., p. 77. Bühler (p. 78) feels that of all these hypotheses that which connects the Brāhmī with the Egyptian numerals is the most plausible, although he does not adduce any convincing proof. Th. Henri Martin, "Les signes numéraux et l'arithmétique chez les peuples de l'antiquité et du moyen âge" (being an examination of Cantor's Mathematische Beiträge zum Culturleben der Völker), Annali di matematica pura ed applicata, Vol. V, Rome, 1864, pp. 8, 70. Also, same author, "Recherches nouvelles sur l'origine de notre système de numération écrite," Revue Archéologique, 1857, pp. 36, 55. See also the tables given later in this work.
[106] Journal of the Royal Asiatic Society, Bombay Branch, Vol. XXIII.
[107] Loc. cit., reprint, Part I, pp. 12, 17. Bayley's deductions are generally regarded as unwarranted.
[108] The Alphabet; London, 1883, Vol. II, pp. 265, 266, and The Academy of Jan. 28, 1882.
[109] Taylor, The Alphabet, loc. cit., table on p. 266.
[110] Bühler, On the Origin of the Indian Brāhma Alphabet, Strassburg, 1898, footnote, pp. 52, 53.
[111] Albrecht Weber, History of Indian Literature, English ed., Boston, 1878, p. 256: "The Indian figures from 1-9 are abbreviated forms of the initial letters of the numerals themselves...: the zero, too, has arisen out of the first letter of the word ṣunya (empty) (it occurs even in Piñgala). It is the decimal place value of these figures which gives them significance." C. Henry, "Sur l'origine de quelques notations mathématiques," Revue Archéologique, June and July, 1879, attempts to derive the Boethian forms from the initials of Latin words. See also J. Prinsep, "Examination of the Inscriptions from Girnar in Gujerat, and Dhauli in Cuttach," Journal of the Asiatic Society of Bengal, 1838, especially Plate XX, p. 348; this was the first work on the subject.
[112] Bühler, Palaeographie, p. 75, gives the list, with the list of letters (p. 76) corresponding to the number symbols.
[113] For a general discussion of the connection between the numerals and the different kinds of alphabets, see the articles by U. Ceretti, "Sulla origine delle cifre numerali moderne," Rivista di fisica, matematica e scienze naturali, Pisa and Pavia, 1909, anno X, numbers 114, 118, 119, and 120, and continuation in 1910.
[114] This is one of Bühler's hypotheses. See Bayley, loc. cit., reprint p. 4; a good bibliography of original sources is given in this work, p. 38.
[115] Loc. cit., reprint, part I, pp. 12, 17. See also Burnell, loc. cit., p. 64, and tables in plate XXIII.
[116] This was asserted by G. Hager (Memoria sulle cifre arabiche, Milan, 1813, also published in Fundgruben des Orients, Vienna, 1811, and in Bibliothèque Britannique, Geneva, 1812). See also the recent article by Major Charles E. Woodruff, "The Evolution of Modern Numerals from Tally Marks," American Mathematical Monthly, August-September, 1909. Biernatzki, "Die Arithmetik der Chinesen," Crelle's Journal für die reine und angewandte Mathematik, Vol. LII, 1857, pp. 59-96, also asserts the priority of the Chinese claim for a place system and the zero, but upon the flimsiest authority. Ch. de Paravey, Essai sur l'origine unique et hiéroglyphique des chiffres et des lettres de tous les peuples, Paris, 1826; G. Kleinwächter, "The Origin of the Arabic Numerals," China Review, Vol. XI, 1882-1883, pp. 379-381, Vol. XII, pp. 28-30; Biot, "Note sur la connaissance que les Chinois ont eue de la valeur de position des chiffres," Journal Asiatique, 1839, pp. 497-502. A. Terrien de Lacouperie, "The Old Numerals, the Counting-Rods and the Swan-Pan in China," Numismatic Chronicle, Vol. III (3), pp. 297-340, and Crowder B. Moseley, "Numeral Characters: Theory of Origin and Development," American Antiquarian, Vol. XXII, pp. 279-284, both propose to derive our numerals from Chinese characters, in much the same way as is done by Major Woodruff, in the article above cited.
[117] The Greeks, probably following the Semitic custom, used nine letters of the alphabet for the numerals from 1 to 9, then nine others for 10 to 90, and further letters to represent 100 to 900. As the ordinary Greek alphabet was insufficient, containing only twenty-four letters, an alphabet of twenty-seven letters was used.
[118] Institutiones mathematicae, 2 vols., Strassburg, 1593-1596, a somewhat rare work from which the following quotation is taken:
"Quis est harum Cyphrarum autor?
"A quibus hae usitatae syphrarum notae sint inventae: hactenus incertum fuit: meo tamen iudicio, quod exiguum esse fateor: a graecis librarijs (quorum olim magna fuit copia) literae Graecorum quibus veteres Graeci tamquam numerorum notis sunt usi: fuerunt corruptae. vt ex his licet videre.
"Graecorum Literae corruptae.
"Sed qua ratione graecorum literae ita fuerunt corruptae?
"Finxerunt has corruptas Graecorum literarum notas: vel abiectione vt in nota binarij numeri, vel additione vt in ternarij, vel inuersione vt in septenarij, numeri nota, nostrae notae, quibus hodie utimur: ab his sola differunt elegantia, vt apparet."
See also Bayer, Historia regni Graecorum Bactriani, St. Petersburg, 1788, pp. 129-130, quoted by Martin, Recherches nouvelles, etc., loc. cit.
[119] P. D. Huet, Demonstratio
evangelica, Paris, 1769, note to p. 139 on p. 647: "Ab Arabibus vel
ab Indis inventas esse, non vulgus eruditorum modo, sed doctissimi quique
ad hanc diem arbitrati sunt. Ego vero falsum id esse, merosque esse
Graecorum characteres aio; à librariis Graecae linguae ignaris
interpolatos, et diuturna scribendi consuetudine corruptos. Nam primum 1
apex fuit, seu virgula, nota μονάδος. 2, est ipsum
β extremis suis truncatum. γ, si in sinistram partem inclinaveris &
cauda mutilaveris & sinistrum cornu sinistrorsum flexeris, fiet 3.
Res ipsa loquitur 4 ipsissimum esse Δ,
cujus crus sinistrum erigitur κατὰ
κάθετον, & infra
basim descendit; basis vero ipsa ultra crus producta eminet. Vides quam 5
simile sit τῷ  ; infimo tantum semicirculo, qui
sinistrorsum patebat, dextrorsum converso. ἐπίσημον
βαῦ quod ita notabatur
; infimo tantum semicirculo, qui
sinistrorsum patebat, dextrorsum converso. ἐπίσημον
βαῦ quod ita notabatur  , rotundato ventre, pede detracto,
peperit τὸ 6. Ex Ζ basi sua mutilato, ortum est τὸ 7. Si Η inflexis
introrsum apicibus in rotundiorem & commodiorem formam mutaveris,
exurget τὸ 8. At 9
ipsissimum est
, rotundato ventre, pede detracto,
peperit τὸ 6. Ex Ζ basi sua mutilato, ortum est τὸ 7. Si Η inflexis
introrsum apicibus in rotundiorem & commodiorem formam mutaveris,
exurget τὸ 8. At 9
ipsissimum est 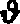 ."
."
I. Weidler, Spicilegium observationum ad historiam notarum numeralium, Wittenberg, 1755, derives them from the Hebrew letters; Dom Augustin Calmet, "Recherches sur l'origine des chiffres d'arithmétique," Mémoires pour l'histoire des sciences et des beaux arts, Trévoux, 1707 (pp. 1620-1635, with two plates), derives the current symbols from the Romans, stating that they are relics of the ancient "Notae Tironianae." These "notes" were part of a system of shorthand invented, or at least perfected, by Tiro, a slave who was freed by Cicero. L. A. Sedillot, "Sur l'origine de nos chiffres," Atti dell' Accademia pontificia dei nuovi Lincei, Vol. XVIII, 1864-1865, pp. 316-322, derives the Arabic forms from the Roman numerals.
[120] Athanasius Kircher, Arithmologia sive De abditis Numerorum, mysterijs qua origo, antiquitas & fabrica Numerorum exponitur, Rome, 1665.
[121] See Suter, Die Mathematiker und Astronomen der Araber, p. 100.
[122] "Et hi numeri sunt numeri Indiani, a Brachmanis Indiae Sapientibus ex figura circuli secti inuenti."
[123] V. A. Smith, The Early History of India, Oxford, 2d ed., 1908, p. 333.
[124] C. J. Ball, "An Inscribed Limestone Tablet from Sippara," Proceedings of the Society of Biblical Archæology, Vol. XX, p. 25 (London, 1898). Terrien de Lacouperie states that the Chinese used the circle for 10 before the beginning of the Christian era. [Catalogue of Chinese Coins, London, 1892, p. xl.]
[125] For a purely fanciful derivation from the corresponding number of strokes, see W. W. R. Ball, A Short Account of the History of Mathematics, 1st ed., London, 1888, p. 147; similarly J. B. Reveillaud, Essai sur les chiffres arabes, Paris, 1883; P. Voizot, "Les chiffres arabes et leur origine," La Nature, 1899, p. 222; G. Dumesnil, "De la forme des chiffres usuels," Annales de l'université de Grenoble, 1907, Vol. XIX, pp. 657-674, also a note in Revue Archéologique, 1890, Vol. XVI (3), pp. 342-348; one of the earliest references to a possible derivation from points is in a work by Bettino entitled Apiaria universae philosophiae mathematicae in quibus paradoxa et noua machinamenta ad usus eximios traducta, et facillimis demonstrationibus confirmata, Bologna, 1545, Vol. II, Apiarium XI, p. 5.
[126] Alphabetum Barmanum, Romae, MDCCLXXVI, p. 50. The 1 is evidently Sanskrit, and the 4, 7, and possibly 9 are from India.
[127] Alphabetum Grandonico-Malabaricum, Romae, MDCCLXXII, p. 90. The zero is not used, but the symbols for 10, 100, and so on, are joined to the units to make the higher numbers.
[128] Alphabetum Tangutanum, Romae, MDCCLXXIII, p. 107. In a Tibetan MS. in the library of Professor Smith, probably of the eighteenth century, substantially these forms are given.
[129] Bayley, loc. cit., plate II. Similar forms to these here shown, and numerous other forms found in India, as well as those of other oriental countries, are given by A. P. Pihan, Exposé des signes de numération usités chez les peuples orientaux anciens et modernes, Paris, 1860.
[130] Bühler, loc. cit., p. 80; J. F. Fleet, Corpus inscriptionum Indicarum, Vol. III, Calcutta, 1888. Lists of such words are given also by Al-Bīrūnī in his work India; by Burnell, loc. cit.; by E. Jacquet, "Mode d'expression symbolique des nombres employé par les Indiens, les Tibétains et les Javanais," Journal Asiatique, Vol. XVI, Paris, 1835.
[131] This date is given by Fleet, loc. cit., Vol. III, p. 73, as the earliest epigraphical instance of this usage in India proper.
[132] Weber, Indische Studien, Vol. VIII, p. 166 seq.
[133] Journal of the Royal Asiatic Society, Vol. I (N.S.), p. 407.
[134] VIII, 20, 21.
[135] Th. H. Martin, Les signes numéraux ..., Rome, 1864; Lassen, Indische Alterthumskunde, Vol. II, 2d ed., Leipzig and London, 1874, p. 1153.
[136] But see Burnell, loc. cit., and Thibaut, Astronomie, Astrologie und Mathematik, p. 71.
[137] A. Barth, "Inscriptions Sanscrites du Cambodge," in the Notices et extraits des Mss. de la Bibliothèque nationale, Vol. XXVII, Part I, pp. 1-180, 1885; see also numerous articles in Journal Asiatique, by Aymonier.
[138] Bühler, loc. cit., p. 82.
[139] Loc. cit., p. 79.
[140] Bühler, loc. cit., p. 83. The Hindu astrologers still use an alphabetical system of numerals. [Burnell, loc. cit., p. 79.]
[141] Well could Ramus say, "Quicunq; autem fuerit inventor decem notarum laudem magnam meruit."
[142] Al-Bīrūnī gives lists.
[143] Propagation, loc. cit., p. 443.
[144] See the quotation from The Light of Asia in Chapter II, p. 16.
[145] The nine ciphers were called aṅka.
[146] "Zur Geschichte des indischen Ziffernsystems," Zeitschrift für die Kunde des Morgenlandes, Vol. IV, 1842, pp. 74-83.
[147] It is found in the Bakhṣālī MS. of an elementary arithmetic which Hoernle placed, at first, about the beginning of our era, but the date is much in question. G. Thibaut, loc. cit., places it between 700 and 900 A.D.; Cantor places the body of the work about the third or fourth century A.D., Geschichte der Mathematik, Vol. I (3), p. 598.
[148] For the opposite side of the case see G. R. Kaye, "Notes on Indian Mathematics, No. 2.—Āryabhaṭa," Journ. and Proc. of the Asiatic Soc. of Bengal, Vol. IV, 1908, pp. 111-141.
[149] He used one of the alphabetic systems explained above. This ran up to 1018 and was not difficult, beginning as follows:
the same letter (ka) appearing in the successive consonant forms, ka, kha, ga, gha, etc. See C. I. Gerhardt, Über die Entstehung und Ausbreitung des dekadischen Zahlensystems, Programm, p. 17, Salzwedel, 1853, and Études historiques sur l'arithmétique de position, Programm, p. 24, Berlin, 1856; E. Jacquet, Mode d'expression symbolique des nombres, loc. cit., p. 97; L. Rodet, "Sur la véritable signification de la notation numérique inventée par Āryabhata," Journal Asiatique, Vol. XVI (7), pp. 440-485. On the two Āryabhaṭas see Kaye, Bibl. Math., Vol. X (3), p. 289.
[150] Using kha, a synonym of śūnya. [Bayley, loc. cit., p. 22, and L. Rodet, Journal Asiatique, Vol. XVI (7), p. 443.]
[151] Varāha-Mihira, Pañcasiddhāntikā, translated by G. Thibaut and M. S. Dvivedī, Benares, 1889; see Bühler, loc. cit., p. 78; Bayley, loc. cit., p. 23.
[152] Bṛhat Saṃhitā, translated by Kern, Journal of the Royal Asiatic Society, 1870-1875.
[153] It is stated by Bühler in a personal letter to Bayley (loc. cit., p. 65) that there are hundreds of instances of this usage in the Bṛhat Saṃhitā. The system was also used in the Pañcasiddhāntikā as early as 505 A.D. [Bühler, Palaeographie, p. 80, and Fleet, Journal of the Royal Asiatic Society, 1910, p. 819.]
[154] Cantor, Geschichte der Mathematik, Vol. I (3), p. 608.
[155] Bühler, loc. cit., p. 78.
[156] Bayley, p. 38.
[157] Noviomagus, in his De numeris libri duo, Paris, 1539, confesses his ignorance as to the origin of the zero, but says: "D. Henricus Grauius, vir Graecè & Hebraicè eximè doctus, Hebraicam originem ostendit," adding that Valla "Indis Orientalibus gentibus inventionem tribuit."
[158] See Essays, Vol. II, pp. 287 and 288.
[159] Vol. XXX, p. 205 seqq.
[160] Loc. cit., p. 284 seqq.
[161] Colebrooke, loc. cit., p. 288.
[162] Loc. cit., p. 78.
[163] Hereafter, unless expressly stated to the contrary, we shall use the word "numerals" to mean numerals with place value.
[164] "The Gurjaras of Rājputāna and Kanauj," in Journal of the Royal Asiatic Society, January and April, 1909.
[165] Vol. IX, 1908, p. 248.
[166] Epigraphia Indica, Vol. IX, pp. 193 and 198.
[167] Epigraphia Indica, Vol. IX, p. 1.
[168] Loc. cit., p. 71.
[169] Thibaut, p. 71.
[170] "Est autem in aliquibus figurarum istaram apud multos diuersitas. Quidam enim septimam hanc figuram representant," etc. [Boncompagni, Trattati, p. 28.] Eneström has shown that very likely this work is incorrectly attributed to Johannes Hispalensis. [Bibliotheca Mathematica, Vol. IX (3), p. 2.]
[171] Indische Palaeographie, Tafel IX.
[172] Edited by Bloomfield and Garbe, Baltimore, 1901, containing photographic reproductions of the manuscript.
[173] Bakhṣālī MS. See page 43; Hoernle, R., The Indian Antiquary, Vol. XVII, pp. 33-48, 1 plate; Hoernle, Verhandlungen des VII. Internationalen Orientalisten-Congresses, Arische Section, Vienna, 1888, "On the Bakshālī Manuscript," pp. 127-147, 3 plates; Bühler, loc. cit.
[174] 3, 4, 6, from H. H. Dhruva, "Three Land-Grants from Sankheda," Epigraphia Indica, Vol. II, pp. 19-24 with plates; date 595 A.D. 7, 1, 5, from Bhandarkar, "Daulatabad Plates," Epigraphia Indica, Vol. IX, part V; date c. 798 A.D.
[175] 8, 7, 2, from "Buckhala Inscription of Nagabhatta," Bhandarkar, Epigraphia Indica, Vol. IX, part V; date 815 A.D. 5 from "The Morbi Copper-Plate," Bhandarkar, The Indian Antiquary, Vol. II, pp. 257-258, with plate; date 804 A.D. See Bühler, loc. cit.
[176] 8 from the above Morbi Copper-Plate. 4, 5, 7, 9, and 0, from "Asni Inscription of Mahipala," The Indian Antiquary, Vol. XVI, pp. 174-175; inscription is on red sandstone, date 917 A.D. See Bühler.
[177] 8, 9, 4, from "Rashtrakuta Grant of Amoghavarsha," J. F. Fleet, The Indian Antiquary, Vol. XII, pp. 263-272; copper-plate grant of date c. 972 A.D. See Bühler. 7, 3, 5, from "Torkhede Copper-Plate Grant of the Time of Govindaraja of Gujerat," Fleet, Epigraphia Indica, Vol. III, pp. 53-58. See Bühler.
[178] From "A Copper-Plate Grant of King Tritochanapâla Chanlukya of Lāṭadeśa," H.H. Dhruva, Indian Antiquary, Vol. XII, pp. 196-205; date 1050 A.D. See Bühler.
[179] Burnell, A. C., South Indian Palæography, plate XXIII, Telugu-Canarese numerals of the eleventh century. See Bühler.
[180] From a manuscript of the second half of the thirteenth century, reproduced in "Della vita e delle opere di Leonardo Pisano," Baldassare Boncompagni, Rome, 1852, in Atti dell' Accademia Pontificia dei nuovi Lincei, anno V.
[181] From a fourteenth-century manuscript, as reproduced in Della vita etc., Boncompagni, loc. cit.
[182] From a Tibetan MS. in the library of D. E. Smith.
[183] From a Tibetan block-book in the library of D. E. Smith.
[184] Śāradā numerals from The Kashmirian Atharva-Veda, reproduced by chromophotography from the manuscript in the University Library at Tübingen, Bloomfield and Garbe, Baltimore, 1901. Somewhat similar forms are given under "Numération Cachemirienne," by Pihan, Exposé etc., p. 84.
[185] Franz X. Kugler, Die Babylonische Mondrechnung, Freiburg i. Br., 1900, in the numerous plates at the end of the book; practically all of these contain the symbol to which reference is made. Cantor, Geschichte, Vol. I, p. 31.
[186] F. X. Kugler, Sternkunde und Sterndienst in Babel, I. Buch, from the beginnings to the time of Christ, Münster i. Westfalen, 1907. It also has numerous tables containing the above zero.
[187] From a letter to D. E. Smith, from G. F. Hill of the British Museum. See also his monograph "On the Early Use of Arabic Numerals in Europe," in Archæologia, Vol. LXII (1910), p. 137.
[188] R. Hoernle, "The Bakshālī Manuscript," Indian Antiquary, Vol. XVII, pp. 33-48 and 275-279, 1888; Thibaut, Astronomie, Astrologie und Mathematik, p. 75; Hoernle, Verhandlungen, loc. cit., p. 132.
[189] Bayley, loc. cit., Vol. XV, p. 29. Also Bendall, "On a System of Numerals used in South India," Journal of the Royal Asiatic Society, 1896, pp. 789-792.
[190] V. A. Smith, The Early History of India, 2d ed., Oxford, 1908, p. 14.
[191] Colebrooke, Algebra, with Arithmetic and Mensuration, from the Sanskrit of Brahmegupta and Bháscara, London, 1817, pp. 339-340.
[192] Ibid., p. 138.
[193] D. E. Smith, in the Bibliotheca Mathematica, Vol. IX (3), pp. 106-110.
[194] As when we use three dots (...).
[195] "The Hindus call the nought explicitly śūnyabindu 'the dot marking a blank,' and about 500 A.D. they marked it by a simple dot, which latter is commonly used in inscriptions and MSS. in order to mark a blank, and which was later converted into a small circle." [Bühler, On the Origin of the Indian Alphabet, p. 53, note.]
[196] Fazzari, Dell' origine delle parole zero e cifra, Naples, 1903.
[197] E. Wappler, "Zur Geschichte der Mathematik im 15. Jahrhundert," in the Zeitschrift für Mathematik und Physik, Vol. XLV, Hist.-lit. Abt., p. 47. The manuscript is No. C. 80, in the Dresden library.
[198] J. G. Prändel, Algebra nebst ihrer literarischen Geschichte, p. 572, Munich, 1795.
[199] See the table, p. 23. Does the fact that the early European arithmetics, following the Arab custom, always put the 0 after the 9, suggest that the 0 was derived from the old Hindu symbol for 10?
[200] Bayley, loc. cit., p. 48. From this fact Delambre (Histoire de l'astronomie ancienne) inferred that Ptolemy knew the zero, a theory accepted by Chasles, Aperçu historique sur l'origine et le développement des méthodes en géométrie, 1875 ed., p. 476; Nesselmann, however, showed (Algebra der Griechen, 1842, p. 138), that Ptolemy merely used ο for οὐδὲν, with no notion of zero. See also G. Fazzari, "Dell' origine delle parole zero e cifra," Ateneo, Anno I, No. 11, reprinted at Naples in 1903, where the use of the point and the small cross for zero is also mentioned. Th. H. Martin, Les signes numéraux etc., reprint p. 30, and J. Brandis, Das Münz-, Mass- und Gewichtswesen in Vorderasien bis auf Alexander den Grossen, Berlin, 1866, p. 10, also discuss this usage of ο, without the notion of place value, by the Greeks.
[201] Al-Battānī sive Albatenii opus astronomicum. Ad fidem codicis escurialensis arabice editum, latine versum, adnotationibus instructum a Carolo Alphonso Nallino, 1899-1907. Publicazioni del R. Osservatorio di Brera in Milano, No. XL.
[202] Loc. cit., Vol. II, p. 271.
[203] C. Henry, "Prologus N. Ocreati in Helceph ad Adelardum Batensem magistrum suum," Abhandlungen zur Geschichte der Mathematik, Vol. III, 1880.
[204] Max. Curtze, "Ueber eine Algorismus-Schrift des XII. Jahrhunderts," Abhandlungen zur Geschichte der Mathematik, Vol. VIII, 1898, pp. 1-27; Alfred Nagl, "Ueber eine Algorismus-Schrift des XII. Jahrhunderts und über die Verbreitung der indisch-arabischen Rechenkunst und Zahlzeichen im christl. Abendlande," Zeitschrift für Mathematik und Physik, Hist.-lit. Abth., Vol. XXXIV, pp. 129-146 and 161-170, with one plate.
[205] "Byzantinische Analekten," Abhandlungen zur Geschichte der Mathematik, Vol. IX, pp. 161-189.
[206] 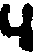 or
or  for 0.
for 0. 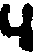 also used for 5.
also used for 5.  for 13. [Heiberg, loc. cit.]
for 13. [Heiberg, loc. cit.]
[207] Gerhardt, Études historiques sur l'arithmétique de position, Berlin, 1856, p. 12; J. Bowring, The Decimal System in Numbers, Coins, & Accounts, London, 1854, p. 33.
[208] Karabacek, Wiener Zeitschrift für die Kunde des Morgenlandes, Vol. XI, p. 13; Führer durch die Papyrus-Ausstellung Erzherzog Rainer, Vienna, 1894, p. 216.
[209] In the library of G. A. Plimpton, Esq.
[210] Cantor, Geschichte, Vol. I (3), p. 674; Y. Mikami, "A Remark on the Chinese Mathematics in Cantor's Geschichte der Mathematik," Archiv der Mathematik und Physik, Vol. XV (3), pp. 68-70.
[211] Of course the earlier historians made innumerable guesses as to the origin of the word cipher. E.g. Matthew Hostus, De numeratione emendata, Antwerp, 1582, p. 10, says: "Siphra vox Hebræam originem sapit refértque: & ut docti arbitrantur, à verbo saphar, quod Ordine numerauit significat. Unde Sephar numerus est: hinc Siphra (vulgo corruptius). Etsi verò gens Iudaica his notis, quæ hodie Siphræ vocantur, usa non fuit: mansit tamen rei appellatio apud multas gentes." Dasypodius, Institutiones mathematicae, Vol. I, 1593, gives a large part of this quotation word for word, without any mention of the source. Hermannus Hugo, De prima scribendi origine, Trajecti ad Rhenum, 1738, pp. 304-305, and note, p. 305; Karl Krumbacher, "Woher stammt das Wort Ziffer (Chiffre)?", Études de philologie néo-grecque, Paris, 1892.
[212] Bühler, loc. cit., p. 78 and p. 86.
[213] Fazzari, loc. cit., p. 4. So Elia Misrachi (1455-1526) in his posthumous Book of Number, Constantinople, 1534, explains sifra as being Arabic. See also Steinschneider, Bibliotheca Mathematica, 1893, p. 69, and G. Wertheim, Die Arithmetik des Elia Misrachi, Programm, Frankfurt, 1893.
[214] "Cum his novem figuris, et cum hoc signo 0, quod arabice zephirum appellatur, scribitur quilibet numerus."
[215] τζίφρα, a form also used by
Neophytos (date unknown, probably c. 1330). It is curious that Finaeus
(1555 ed., f. 2) used the form tziphra throughout. A. J. H.
Vincent ["Sur l'origine de nos chiffres," Notices et Extraits des
MSS., Paris, 1847, pp. 143-150] says: "Ce cercle fut nommé par les
uns, sipos, rota, galgal ...; par les autres tsiphra (de
צפר, couronne ou
diadème) ou ciphra (de ספר,
numération)." Ch. de Paravey, Essai sur l'origine unique et
hiéroglyphique des chiffres et des lettres de tous les peuples,
Paris, 1826, p. 165, a rather fanciful work, gives "vase, vase arrondi et
fermé par un couvercle, qui est le symbole de la 10e Heure,  ," among the Chinese; also
"Tsiphron Zéron, ou tout à fait vide en arabe, τζίφρα en grec ... d'où chiffre
(qui dérive plutôt, suivant nous, de l'Hébreu Sepher,
compter.")
," among the Chinese; also
"Tsiphron Zéron, ou tout à fait vide en arabe, τζίφρα en grec ... d'où chiffre
(qui dérive plutôt, suivant nous, de l'Hébreu Sepher,
compter.")
[216] "Compilatus a Magistro Jacobo de Florentia apud montem pesalanum," and described by G. Lami in his Catalogus codicum manuscriptorum qui in bibliotheca Riccardiana Florentiæ adservantur. See Fazzari, loc. cit., p. 5.
[217] "Et doveto sapere chel zeuero per se solo non significa nulla ma è potentia di fare significare, ... Et decina o centinaia o migliaia non si puote scrivere senza questo segno 0. la quale si chiama zeuero." [Fazzari, loc. cit., p. 5.]
[218] Ibid., p. 6.
[219] Avicenna (980-1036), translation by Gasbarri et François, "più il punto (gli Arabi adoperavano il punto in vece dello zero il cui segno 0 in arabo si chiama zepiro donde il vocabolo zero), che per sè stesso non esprime nessun numero." This quotation is taken from D. C. Martines, Origine e progressi dell' aritmetica, Messina, 1865.
[220] Leo Jordan, "Materialien zur Geschichte der arabischen Zahlzeichen in Frankreich," Archiv für Kulturgeschichte, Berlin, 1905, pp. 155-195, gives the following two schemes of derivation, (1) "zefiro, zeviro, zeiro, zero," (2) "zefiro, zefro, zevro, zero."
[221] Köbel (1518 ed., f. A_4) speaks of the numerals in general as "die der gemain man Zyfer nendt." Recorde (Grounde of Artes, 1558 ed., f. B_6) says that the zero is "called priuatly a Cyphar, though all the other sometimes be likewise named."
[222] "Decimo X 0 theca, circul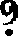 cifra sive figura nihili
appelat′." [Enchiridion Algorismi, Cologne, 1501.] Later,
"quoniam de integris tam in cifris quam in proiectilibus,"—the word
proiectilibus referring to markers "thrown" and used on an abacus,
whence the French jetons and the English expression "to
cast an account."
cifra sive figura nihili
appelat′." [Enchiridion Algorismi, Cologne, 1501.] Later,
"quoniam de integris tam in cifris quam in proiectilibus,"—the word
proiectilibus referring to markers "thrown" and used on an abacus,
whence the French jetons and the English expression "to
cast an account."
[223] "Decima vero o dicitur teca, circulus, vel cyfra vel figura nichili." [Maximilian Curtze, Petri Philomeni de Dacia in Algorismum Vulgarem Johannis de Sacrobosco commentarius, una cum Algorismo ipso, Copenhagen, 1897, p. 2.] Curtze cites five manuscripts (fourteenth and fifteenth centuries) of Dacia's commentary in the libraries at Erfurt, Leipzig, and Salzburg, in addition to those given by Eneström, Öfversigt af Kongl. Vetenskaps-Akademiens Förhandlingar, 1885, pp. 15-27, 65-70; 1886, pp. 57-60.
[224] Curtze, loc. cit., p. VI.
[225] Rara Mathematica, London, 1841, chap, i, "Joannis de Sacro-Bosco Tractatus de Arte Numerandi."
[226] Smith, Rara Arithmetica, Boston, 1909.
[227] In the 1484 edition, Borghi uses the form "çefiro: ouero nulla:" while in the 1488 edition he uses "zefiro: ouero nulla," and in the 1540 edition, f. 3, appears "Chiamata zero, ouero nulla." Woepcke asserted that it first appeared in Calandri (1491) in this sentence: "Sono dieci le figure con le quali ciascuno numero si può significare: delle quali n'è una che si chiama zero: et per se sola nulla significa." (f. 4). [See Propagation, p. 522.]
[228] Boncompagni Bulletino, Vol. XVI, pp. 673-685.
[229] Leo Jordan, loc. cit. In the Catalogue of MSS., Bibl. de l'Arsenal, Vol. III, pp. 154-156, this work is No. 2904 (184 S.A.F.), Bibl. Nat., and is also called Petit traicté de algorisme.
[230] Texada (1546) says that there are "nueue letros yvn zero o cifra" (f. 3).
[231] Savonne (1563, 1751 ed., f. 1): "Vne ansi formee (o) qui s'appelle nulle, & entre marchans zero," showing the influence of Italian names on French mercantile customs. Trenchant (Lyons, 1566, 1578 ed., p. 12) also says: "La derniere qui s'apele nulle, ou zero;" but Champenois, his contemporary, writing in Paris in 1577 (although the work was not published until 1578), uses "cipher," the Italian influence showing itself less in this center of university culture than in the commercial atmosphere of Lyons.
[232] Thus Radulph of Laon (c.
1100): "Inscribitur in ultimo ordine et figura  sipos nomine, quae, licet numerum
nullum signitet, tantum ad alia quaedam utilis, ut insequentibus
declarabitur." ["Der Arithmetische Tractat des Radulph von Laon,"
Abhandlungen zur Geschichte der Mathematik, Vol. V, p. 97, from a
manuscript of the thirteenth century.] Chasles (Comptes rendus, t.
16, 1843, pp. 1393, 1408) calls attention to the fact that Radulph did
not know how to use the zero, and he doubts if the sipos was really
identical with it. Radulph says: "... figuram, cui sipos nomen est
sipos nomine, quae, licet numerum
nullum signitet, tantum ad alia quaedam utilis, ut insequentibus
declarabitur." ["Der Arithmetische Tractat des Radulph von Laon,"
Abhandlungen zur Geschichte der Mathematik, Vol. V, p. 97, from a
manuscript of the thirteenth century.] Chasles (Comptes rendus, t.
16, 1843, pp. 1393, 1408) calls attention to the fact that Radulph did
not know how to use the zero, and he doubts if the sipos was really
identical with it. Radulph says: "... figuram, cui sipos nomen est  in motum rotulae formatam nullius
numeri significatione inscribi solere praediximus," and thereafter uses
rotula. He uses the sipos simply as a kind of marker on the
abacus.
in motum rotulae formatam nullius
numeri significatione inscribi solere praediximus," and thereafter uses
rotula. He uses the sipos simply as a kind of marker on the
abacus.
[233] Rabbi ben Ezra (1092-1168) used both גלגל, galgal (the Hebrew for wheel), and ספרא, sifra. See M. Steinschneider, "Die Mathematik bei den Juden," in Bibliotheca Mathematica, 1893, p. 69, and Silberberg, Das Buch der Zahl des R. Abraham ibn Esra, Frankfurt a. M., 1895, p. 96, note 23; in this work the Hebrew letters are used for numerals with place value, having the zero.
[234] E.g., in the twelfth-century Liber aligorismi (see Boncompagni's Trattati, II, p. 28). So Ramus (Libri II, 1569 ed., p. 1) says: "Circulus quæ nota est ultima: nil per se significat." (See also the Schonerus ed. of Ramus, 1586, p. 1.)
[235] "Und wirt das ringlein o. die Ziffer genant die nichts bedeut." [Köbel's Rechenbuch, 1549 ed., f. 10, and other editions.]
[236] I.e. "circular figure," our
word notation having come from the medieval nota. Thus
Tzwivel (1507, f. 2) says: "Nota autem circularis .o. per se sumpta nihil
vsus habet. alijs tamen adiuncta earum significantiam et auget et ordinem
permutat quantum quo ponit ordinem. vt adiuncta note binarij hoc modo 20
facit eam significare bis decem etc." Also (ibid., f. 4), "figura
circularis," "circularis nota." Clichtoveus (1503 ed., f. XXXVII) calls it "nota aut circularis o," "circularis
nota," and "figura circularis." Tonstall (1522, f. B_3) says of it:
"Decimo uero nota ad formam  litteræ circulari figura est: quam alij circulum, uulgus cyphram
uocat," and later (f. C_4) speaks of the "circulos." Grammateus, in his
Algorismus de integris (Erfurt, 1523, f. A_2), speaking of the
nine significant figures, remarks: "His autem superadditur decima figura
circularis ut 0 existens que ratione sua nihil significat." Noviomagus
(De Numeris libri II, Paris, 1539, chap. xvi, "De notis numerorum,
quas zyphras vocant") calls it "circularis nota, quam ex his solam, alij
sipheram, Georgius Valla zyphram."
litteræ circulari figura est: quam alij circulum, uulgus cyphram
uocat," and later (f. C_4) speaks of the "circulos." Grammateus, in his
Algorismus de integris (Erfurt, 1523, f. A_2), speaking of the
nine significant figures, remarks: "His autem superadditur decima figura
circularis ut 0 existens que ratione sua nihil significat." Noviomagus
(De Numeris libri II, Paris, 1539, chap. xvi, "De notis numerorum,
quas zyphras vocant") calls it "circularis nota, quam ex his solam, alij
sipheram, Georgius Valla zyphram."
[237] Huswirt, as above. Ramus (Scholae mathematicae, 1569 ed., p. 112) discusses the name interestingly, saying: "Circulum appellamus cum multis, quam alii thecam, alii figuram nihili, alii figuram privationis, seu figuram nullam vocant, alii ciphram, cùm tamen hodie omnes hæ notæ vulgò ciphræ nominentur, & his notis numerare idem sit quod ciphrare." Tartaglia (1592 ed., f. 9) says: "si chiama da alcuni tecca, da alcuni circolo, da altri cifra, da altri zero, & da alcuni altri nulla."
[238] "Quare autem aliis
nominibus vocetur, non dicit auctor, quia omnia alia nomina habent
rationem suae lineationis sive figurationis. Quia rotunda est, dicitur
haec figura teca ad similitudinem tecae. Teca enim est ferrum figurae
rotundae, quod ignitum solet in quibusdam regionibus imprimi fronti vel
maxillae furis seu latronum." [Loc. cit., p. 26.] But in Greek
theca ( , θήκη) is a place to put something, a
receptacle. If a vacant column, e.g. in the abacus, was so called, the
initial might have given the early forms
, θήκη) is a place to put something, a
receptacle. If a vacant column, e.g. in the abacus, was so called, the
initial might have given the early forms  and
and 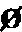 for the zero.
for the zero.
[239] Buteo, Logistica, Lyons, 1559. See also Wertheim in the Bibliotheca Mathematica, 1901, p. 214.
[240] "0 est appellee chiffre ou nulle ou figure de nulle valeur." [La Roche, L'arithmétique, Lyons, 1520.]
[241] "Decima autem figura nihil uocata," "figura nihili (quam etiam cifram uocant)." [Stifel, Arithmetica integra, 1544, f. 1.]
[242] "Zifra, & Nulla uel figura Nihili." [Scheubel, 1545, p. 1 of ch. 1.] Nulla is also used by Italian writers. Thus Sfortunati (1545 ed., f. 4) says: "et la decima nulla & e chiamata questa decima zero;" Cataldi (1602, p. 1): "La prima, che è o, si chiama nulla, ouero zero, ouero niente." It also found its way into the Dutch arithmetics, e.g. Raets (1576, 1580 ed., f. A_3): "Nullo dat ist niet;" Van der Schuere (1600, 1624 ed., f. 7); Wilkens (1669 ed., p. 1). In Germany Johann Albert (Wittenberg, 1534) and Rudolff (1526) both adopted the Italian nulla and popularized it. (See also Kuckuck, Die Rechenkunst im sechzehnten Jahrhundert, Berlin, 1874, p. 7; Günther, Geschichte, p. 316.)
[243] "La dixième s'appelle chifre vulgairement: les vns l'appellant zero: nous la pourrons appeller vn Rien." [Peletier, 1607 ed., p. 14.]
[244] It appears in the Polish arithmetic of Klos (1538) as cyfra. "The Ciphra 0 augmenteth places, but of himselfe signifieth not," Digges, 1579, p. 1. Hodder (10th ed., 1672, p. 2) uses only this word (cypher or cipher), and the same is true of the first native American arithmetic, written by Isaac Greenwood (1729, p. 1). Petrus de Dacia derives cyfra from circumference. "Vocatur etiam cyfra, quasi circumfacta vel circumferenda, quod idem est, quod circulus non habito respectu ad centrum." [Loc. cit., p. 26.]
[245] Opera mathematica, 1695, Oxford, Vol. I, chap. ix, Mathesis universalis, "De figuris numeralibus," pp. 46-49; Vol. II, Algebra, p. 10.
[246] Martin, Origine de notre système de numération écrite, note 149, p. 36 of reprint, spells τσίφρα from Maximus Planudes, citing Wallis as an authority. This is an error, for Wallis gives the correct form as above.
Alexander von Humboldt, "Über die bei verschiedenen Völkern üblichen Systeme von Zahlzeichen und über den Ursprung des Stellenwerthes in den indischen Zahlen," Crelle's Journal für reine und angewandte Mathematik, Vol. IV, 1829, called attention to the work ἀριθμοὶ Ἰνδικοί of the monk Neophytos, supposed to be of the fourteenth century. In this work the forms τζύφρα and τζύμφρα appear. See also Boeckh, De abaco Graecorum, Berlin, 1841, and Tannery, "Le Scholie du moine Néophytos," Revue Archéologique, 1885, pp. 99-102. Jordan, loc. cit., gives from twelfth and thirteenth century manuscripts the forms cifra, ciffre, chifras, and cifrus. Du Cange, Glossarium mediae et infimae Latinitatis, Paris, 1842, gives also chilerae. Dasypodius, Institutiones Mathematicae, Strassburg, 1593-1596, adds the forms zyphra and syphra. Boissière, L'art d'arythmetique contenant toute dimention, tres-singulier et commode, tant pour l'art militaire que autres calculations, Paris, 1554: "Puis y en a vn autre dict zero lequel ne designe nulle quantité par soy, ains seulement les loges vuides."
[247] Propagation, pp. 27, 234, 442. Treutlein, "Das Rechnen im 16. Jahrhundert," Abhandlungen zur Geschichte der Mathematik, Vol. I, p. 5, favors the same view. It is combated by many writers, e.g. A. C. Burnell, loc. cit., p. 59. Long before Woepcke, I. F. and G. I. Weidler, De characteribus numerorum vulgaribus et eorum aetatibus, Wittenberg, 1727, asserted the possibility of their introduction into Greece by Pythagoras or one of his followers: "Potuerunt autem ex oriente, uel ex phoenicia, ad graecos traduci, uel Pythagorae, uel eius discipulorum auxilio, cum aliquis eo, proficiendi in literis causa, iter faceret, et hoc quoque inuentum addisceret."
[248] E.g., they adopted the Greek numerals in use in Damascus and Syria, and the Coptic in Egypt. Theophanes (758-818 A.D.), Chronographia, Scriptores Historiae Byzantinae, Vol. XXXIX, Bonnae, 1839, p. 575, relates that in 699 A.D. the caliph Walīd forbade the use of the Greek language in the bookkeeping of the treasury of the caliphate, but permitted the use of the Greek alphabetic numerals, since the Arabs had no convenient number notation: καὶ ἐκώλυσε γράφεσθαι Ἑλληνιστὶ τοὺς δημοσίους τῶν λογοθεσίων κώδικας, ἀλλ' Ἀραβίοις αὐτὰ παρασημαίνεσθαι, χωρὶς τῶν ψήφων, ἐπειδὴ ἀδύνατον τῇ ἐκείνων γλώσσῃ μονάδα ἢ δυάδα ἢ τριάδα ἢ ὀκτὼ ἥμισυ ἢ τρία γράφεσθαι· διὸ καὶ ἕως σήμερόν εἰσιν σὺν αὐτοῖς νοτάριοι Χριστιανοί. The importance of this contemporaneous document was pointed out by Martin, loc. cit. Karabacek, "Die Involutio im arabischen Schriftwesen," Vol. CXXXV of Sitzungsberichte d. phil.-hist. Classe d. k. Akad. d. Wiss., Vienna, 1896, p. 25, gives an Arabic date of 868 A.D. in Greek letters.
[249] The Origin and History of Our Numerals (in Russian), Kiev, 1908; The Independence of European Arithmetic (in Russian), Kiev.
[250] Woepcke, loc. cit., pp. 462, 262.
[251] Woepcke, loc. cit., p. 240. Ḥisāb-al-Ġobār, by an anonymous author, probably Abū Sahl Dunash ibn Tamim, is given by Steinschneider, "Die Mathematik bei den Juden," Bibliotheca Mathematica, 1896, p. 26.
[252] Steinschneider in the Abhandlungen, Vol. III, p. 110.
[253] See his Grammaire arabe, Vol. I, Paris, 1810, plate VIII; Gerhardt, Études, pp. 9-11, and Entstehung etc., p. 8; I. F. Weidler, Spicilegium observationum ad historiam notarum numeralium pertinentium, Wittenberg, 1755, speaks of the "figura cifrarum Saracenicarum" as being different from that of the "characterum Boethianorum," which are similar to the "vulgar" or common numerals; see also Humboldt, loc. cit.
[254] Gerhardt mentions it in his Entstehung etc., p. 8; Woepcke, Propagation, states that these numerals were used not for calculation, but very much as we use Roman numerals. These superposed dots are found with both forms of numerals (Propagation, pp. 244-246).
[255] Gerhardt (Études, p.
9) from a manuscript in the Bibliothèque Nationale. The numeral forms are
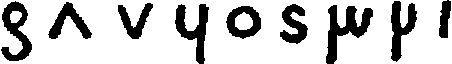 , 20 being indicated by
, 20 being indicated by  and 200 by
and 200 by  . This scheme of zero
dots was also adopted by the Byzantine Greeks, for a manuscript of
Planudes in the Bibliothèque Nationale has numbers like
. This scheme of zero
dots was also adopted by the Byzantine Greeks, for a manuscript of
Planudes in the Bibliothèque Nationale has numbers like 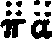 for 8,100,000,000.
See Gerhardt, Études, p. 19. Pihan, Exposé etc., p. 208,
gives two forms, Asiatic and Maghrebian, of "Ghobār" numerals.
for 8,100,000,000.
See Gerhardt, Études, p. 19. Pihan, Exposé etc., p. 208,
gives two forms, Asiatic and Maghrebian, of "Ghobār" numerals.
[256] See Chap. IV.
[257] Possibly as early as the third century A.D., but probably of the eighth or ninth. See Cantor, I (3), p. 598.
[258] Ascribed by the Arabic writer to India.
[259] See Woepcke's description of a manuscript in the Chasles library, "Recherches sur l'histoire des sciences mathématiques chez les orientaux," Journal Asiatique, IV (5), 1859, p. 358, note.
[260] P. 56.
[261] Reinaud, Mémoire sur l'Inde, p. 399. In the fourteenth century one Sihāb al-Dīn wrote a work on which, a scholiast to the Bodleian manuscript remarks: "The science is called Algobar because the inventor had the habit of writing the figures on a tablet covered with sand." [Gerhardt, Études, p. 11, note.]
[262] Gerhardt, Entstehung etc., p. 20.
[263] H. Suter, "Das Rechenbuch des Abū Zakarījā el-Ḥaṣṣār," Bibliotheca Mathematica, Vol. II (3), p. 15.
[264] A. Devoulx, "Les chiffres arabes," Revue Africaine, Vol. XVI, pp. 455-458.
[265] Kitāb al-Fihrist, G. Flügel, Leipzig, Vol. I, 1871, and Vol. II, 1872. This work was published after Professor Flügel's death by J. Roediger and A. Mueller. The first volume contains the Arabic text and the second volume contains critical notes upon it.
[266] Like those of line 5 in the illustration on page 69.
[267] Woepcke, Recherches sur l'histoire des sciences mathématiques chez les orientaux, loc. cit.; Propagation, p. 57.
[268] Al-Ḥaṣṣār's forms, Suter, Bibliotheca Mathematica, Vol. II (3), p. 15.
[269] Woepcke, Sur une donnée historique, etc., loc. cit. The name ġobār is not used in the text. The manuscript from which these are taken is the oldest (970 A.D.) Arabic document known to contain all of the numerals.
[270] Silvestre de Sacy, loc. cit. He gives the ordinary modern Arabic forms, calling them Indien.
[271] Woepcke, "Introduction au calcul Gobārī et Hawāī," Atti dell' accademia pontificia dei nuovi Lincei, Vol. XIX. The adjective applied to the forms in 5 is gobārī and to those in 6 indienne. This is the direct opposite of Woepcke's use of these adjectives in the Recherches sur l'histoire cited above, in which the ordinary Arabic forms (like those in row 5) are called indiens.
These forms are usually written from right to left.
[272] J. G. Wilkinson, The Manners and Customs of the Ancient Egyptians, revised by S. Birch, London, 1878, Vol. II, p. 493, plate XVI.
[273] There is an extensive literature on this "Boethius-Frage." The reader who cares to go fully into it should consult the various volumes of the Jahrbuch über die Fortschritte der Mathematik.
[274] This title was first applied to Roman emperors in posthumous coins of Julius Cæsar. Subsequently the emperors assumed it during their own lifetimes, thus deifying themselves. See F. Gnecchi, Monete romane, 2d ed., Milan, 1900, p. 299.
[275] This is the common spelling of the name, although the more correct Latin form is Boëtius. See Harper's Dict. of Class. Lit. and Antiq., New York, 1897, Vol. I, p. 213. There is much uncertainty as to his life. A good summary of the evidence is given in the last two editions of the Encyclopædia Britannica.
[276] His father, Flavius Manlius Boethius, was consul in 487.
[277] There is, however, no good historic evidence of this sojourn in Athens.
[278] His arithmetic is dedicated to Symmachus: "Domino suo patricio Symmacho Boetius." [Friedlein ed., p. 3.]
[279] It was while here that he wrote De consolatione philosophiae.
[280] It is sometimes given as 525.
[281] There was a medieval tradition that he was executed because of a work on the Trinity.
[282] Hence the Divus in his name.
[283] Thus Dante, speaking of his burial place in the monastery of St. Pietro in Ciel d'Oro, at Pavia, says:
"The saintly soul, that shows
The world's deceitfulness, to all who hear him,
Is, with the sight of all the good that is,
Blest there. The limbs, whence it was driven, lie
Down in Cieldauro; and from martyrdom
And exile came it here."—Paradiso, Canto X.
[284] Not, however, in the mercantile schools. The arithmetic of Boethius would have been about the last book to be thought of in such institutions. While referred to by Bæda (672-735) and Hrabanus Maurus (c. 776-856), it was only after Gerbert's time that the Boëtii de institutione arithmetica libri duo was really a common work.
[285] Also spelled Cassiodorius.
[286] As a matter of fact, Boethius could not have translated any work by Pythagoras on music, because there was no such work, but he did make the theories of the Pythagoreans known. Neither did he translate Nicomachus, although he embodied many of the ideas of the Greek writer in his own arithmetic. Gibbon follows Cassiodorus in these statements in his Decline and Fall of the Roman Empire, chap. xxxix. Martin pointed out with positiveness the similarity of the first book of Boethius to the first five books of Nicomachus. [Les signes numéraux etc., reprint, p. 4.]
[287] The general idea goes back to Pythagoras, however.
[288] J. C. Scaliger in his Poëtice also said of him: "Boethii Severini ingenium, eruditio, ars, sapientia facile provocat omnes auctores, sive illi Graeci sint, sive Latini" [Heilbronner, Hist. math. univ., p. 387]. Libri, speaking of the time of Boethius, remarks: "Nous voyons du temps de Théodoric, les lettres reprendre une nouvelle vie en Italie, les écoles florissantes et les savans honorés. Et certes les ouvrages de Boëce, de Cassiodore, de Symmaque, surpassent de beaucoup toutes les productions du siècle précédent." [Histoire des mathématiques, Vol. I, p. 78.]
[289] Carra de Vaux, Avicenne, Paris, 1900; Woepcke, Sur l'introduction, etc.; Gerhardt, Entstehung etc., p. 20. Avicenna is a corruption from Ibn Sīnā, as pointed out by Wüstenfeld, Geschichte der arabischen Aerzte und Naturforscher, Göttingen, 1840. His full name is Abū ‛Alī al-Ḥosein ibn Sīnā. For notes on Avicenna's arithmetic, see Woepcke, Propagation, p. 502.
[290] On the early travel between the East and the West the following works may be consulted: A. Hillebrandt, Alt-Indien, containing "Chinesische Reisende in Indien," Breslau, 1899, p. 179; C. A. Skeel, Travel in the First Century after Christ, Cambridge, 1901, p. 142; M. Reinaud, "Relations politiques et commerciales de l'empire romain avec l'Asie orientale," in the Journal Asiatique, Mars-Avril, 1863, Vol. I (6), p. 93; Beazley, Dawn of Modern Geography, a History of Exploration and Geographical Science from the Conversion of the Roman Empire to A.D. 1420, London, 1897-1906, 3 vols.; Heyd, Geschichte des Levanthandels im Mittelalter, Stuttgart, 1897; J. Keane, The Evolution of Geography, London, 1899, p. 38; A. Cunningham, Corpus inscriptionum Indicarum, Calcutta, 1877, Vol. I; A. Neander, General History of the Christian Religion and Church, 5th American ed., Boston, 1855, Vol. III, p. 89; R. C. Dutt, A History of Civilization in Ancient India, Vol. II, Bk. V, chap, ii; E. C. Bayley, loc. cit., p. 28 et seq.; A. C. Burnell, loc. cit., p. 3; J. E. Tennent, Ceylon, London, 1859, Vol. I, p. 159; Geo. Turnour, Epitome of the History of Ceylon, London, n.d., preface; "Philalethes," History of Ceylon, London, 1816, chap, i; H. C. Sirr, Ceylon and the Cingalese, London, 1850, Vol. I, chap. ix. On the Hindu knowledge of the Nile see F. Wilford, Asiatick Researches, Vol. III, p. 295, Calcutta, 1792.
[291] G. Oppert, On the Ancient Commerce of India, Madras, 1879, p. 8.
[292] Gerhardt, Études etc., pp. 8, 11.
[293] See Smith's Dictionary of Greek and Roman Biography and Mythology.
[294] P. M. Sykes, Ten Thousand Miles in Persia, or Eight Years in Irán, London, 1902, p. 167. Sykes was the first European to follow the course of Alexander's army across eastern Persia.
[295] Bühler, Indian Brāhma Alphabet, note, p. 27; Palaeographie, p. 2; Herodoti Halicarnassei historia, Amsterdam, 1763, Bk. IV, p. 300; Isaac Vossius, Periplus Scylacis Caryandensis, 1639. It is doubtful whether the work attributed to Scylax was written by him, but in any case the work dates back to the fourth century B.C. See Smith's Dictionary of Greek and Roman Biography.
[296] Herodotus, Bk. III.
[297] Rameses II(?), the Sesoosis of Diodorus Siculus.
[298] Indian Antiquary, Vol. I, p. 229; F. B. Jevons, Manual of Greek Antiquities, London, 1895, p. 386. On the relations, political and commercial, between India and Egypt c. 72 B.C., under Ptolemy Auletes, see the Journal Asiatique, 1863, p. 297.
[299] Sikandar, as the name still remains in northern India.
[300] Harper's Classical Dict., New York, 1897, Vol. I, p. 724; F. B. Jevons, loc. cit., p. 389; J. C. Marshman, Abridgment of the History of India, chaps. i and ii.
[301] Oppert, loc. cit., p. 11. It was at or near this place that the first great Indian mathematician, Āryabhaṭa, was born in 476 A.D.
[302] Bühler, Palaeographie, p. 2, speaks of Greek coins of a period anterior to Alexander, found in northern India. More complete information may be found in Indian Coins, by E. J. Rapson, Strassburg, 1898, pp. 3-7.
[303] Oppert, loc. cit., p. 14; and to him is due other similar information.
[304] J. Beloch, Griechische Geschichte, Vol. III, Strassburg, 1904, pp. 30-31.
[305] E.g., the denarius, the words for hour and minute (ὥρα, λεπτόν), and possibly the signs of the zodiac. [R. Caldwell, Comparative Grammar of the Dravidian Languages, London, 1856, p. 438.] On the probable Chinese origin of the zodiac see Schlegel, loc. cit.
[306] Marie, Vol. II, p. 73; R. Caldwell, loc. cit.
[307] A. Cunningham, loc. cit., p. 50.
[308] C. A. J. Skeel, Travel, loc. cit., p. 14.
[309] Inchiver, from inchi, "the green root." [Indian Antiquary, Vol. I, p. 352.]
[310] In China dating only from the second century A.D., however.
[311] The Italian morra.
[312] J. Bowring, The Decimal System, London, 1854, p. 2.
[313] H. A. Giles, lecture at Columbia University, March 12, 1902, on "China and Ancient Greece."
[314] Giles, loc. cit.
[315] E.g., the names for grape, radish (la-po, ῥάφη), water-lily (si-kua, "west gourds"; σικύα, "gourds"), are much alike. [Giles, loc. cit.]
[316] Epistles, I, 1, 45-46. On the Roman trade routes, see Beazley, loc. cit., Vol. I, p. 179.
[317] Am. Journ. of Archeol., Vol. IV, p. 366.
[318] M. Perrot gives this conjectural restoration of his words: "Ad me ex India regum legationes saepe missi sunt numquam antea visae apud quemquam principem Romanorum." [M. Reinaud, "Relations politiques et commerciales de l'empire romain avec l'Asie orientale," Journ. Asiat., Vol. I (6), p. 93.]
[319] Reinaud, loc. cit., p. 189. Florus, II, 34 (IV, 12), refers to it: "Seres etiam habitantesque sub ipso sole Indi, cum gemmis et margaritis elephantes quoque inter munera trahentes nihil magis quam longinquitatem viae imputabant." Horace shows his geographical knowledge by saying: "Not those who drink of the deep Danube shall now break the Julian edicts; not the Getae, not the Seres, nor the perfidious Persians, nor those born on the river Tanaïs." [Odes, Bk. IV, Ode 15, 21-24.]
[320] "Qua virtutis moderationisque fama Indos etiam ac Scythas auditu modo cognitos pellexit ad amicitiam suam populique Romani ultro per legatos petendam." [Reinaud, loc. cit., p. 180.]
[321] Reinaud, loc. cit., p. 180.
[322] Georgics, II, 170-172. So Propertius (Elegies, III, 4):
Arma deus Caesar dites meditatur ad Indos
Et freta gemmiferi findere classe maris.
"The divine Cæsar meditated carrying arms against opulent India, and with his ships to cut the gem-bearing seas."
[323] Heyd, loc. cit., Vol. I, p. 4.
[324] Reinaud, loc. cit., p. 393.
[325] The title page of Calandri (1491), for example, represents Pythagoras with these numerals before him. [Smith, Rara Arithmetica, p. 46.] Isaacus Vossius, Observationes ad Pomponium Melam de situ orbis, 1658, maintained that the Arabs derived these numerals from the west. A learned dissertation to this effect, but deriving them from the Romans instead of the Greeks, was written by Ginanni in 1753 (Dissertatio mathematica critica de numeralium notarum minuscularum origine, Venice, 1753). See also Mannert, De numerorum quos arabicos vocant vera origine Pythagorica, Nürnberg, 1801. Even as late as 1827 Romagnosi (in his supplement to Ricerche storiche sull' India etc., by Robertson, Vol. II, p. 580, 1827) asserted that Pythagoras originated them. [R. Bombelli, L'antica numerazione italica, Rome, 1876, p. 59.] Gow (Hist. of Greek Math., p. 98) thinks that Iamblichus must have known a similar system in order to have worked out certain of his theorems, but this is an unwarranted deduction from the passage given.
[326] A. Hillebrandt, Alt-Indien, p. 179.
[327] J. C. Marshman, loc. cit., chaps. i and ii.
[328] He reigned 631-579 A.D.; called Nuśīrwān, the holy one.
[329] J. Keane, The Evolution of Geography, London, 1899, p. 38.
[330] The Arabs who lived in and about Mecca.
[331] S. Guyard, in Encyc. Brit., 9th ed., Vol. XVI, p. 597.
[332] Oppert, loc. cit., p. 29.
[333] "At non credendum est id in Autographis contigisse, aut vetustioribus Codd. MSS." [Wallis, Opera omnia, Vol. II, p. 11.]
[334] In Observationes ad Pomponium Melam de situ orbis. The question was next taken up in a large way by Weidler, loc. cit., De characteribus etc., 1727, and in Spicilegium etc., 1755.
[335] The best edition of these works is that of G. Friedlein, Anicii Manlii Torquati Severini Boetii de institutione arithmetica libri duo, de institutione musica libri quinque. Accedit geometria quae fertur Boetii.... Leipzig.... MDCCCLXVII.
[336] See also P. Tannery, "Notes sur la pseudo-géometrie de Boèce," in Bibliotheca Mathematica, Vol. I (3), p. 39. This is not the geometry in two books in which are mentioned the numerals. There is a manuscript of this pseudo-geometry of the ninth century, but the earliest one of the other work is of the eleventh century (Tannery), unless the Vatican codex is of the tenth century as Friedlein (p. 372) asserts.
[337] Friedlein feels that it is partly spurious, but he says: "Eorum librorum, quos Boetius de geometria scripsisse dicitur, investigare veram inscriptionem nihil aliud esset nisi operam et tempus perdere." [Preface, p. v.] N. Bubnov in the Russian Journal of the Ministry of Public Instruction, 1907, in an article of which a synopsis is given in the Jahrbuch über die Fortschritte der Mathematik for 1907, asserts that the geometry was written in the eleventh century.
[338] The most noteworthy of these was for a long time Cantor (Geschichte, Vol. I., 3d ed., pp. 587-588), who in his earlier days even believed that Pythagoras had known them. Cantor says (Die römischen Agrimensoren, Leipzig, 1875, p. 130): "Uns also, wir wiederholen es, ist die Geometrie des Boetius echt, dieselbe Schrift, welche er nach Euklid bearbeitete, von welcher ein Codex bereits in Jahre 821 im Kloster Reichenau vorhanden war, von welcher ein anderes Exemplar im Jahre 982 zu Mantua in die Hände Gerbert's gelangte, von welcher mannigfache Handschriften noch heute vorhanden sind." But against this opinion of the antiquity of MSS. containing these numerals is the important statement of P. Tannery, perhaps the most critical of modern historians of mathematics, that none exists earlier than the eleventh century. See also J. L. Heiberg in Philologus, Zeitschrift f. d. klass. Altertum, Vol. XLIII, p. 508.
Of Cantor's predecessors, Th. H. Martin was one of the most prominent, his argument for authenticity appearing in the Revue Archéologique for 1856-1857, and in his treatise Les signes numéraux etc. See also M. Chasles, "De la connaissance qu'ont eu les anciens d'une numération décimale écrite qui fait usage de neuf chiffres prenant les valeurs de position," Comptes rendus, Vol. VI, pp. 678-680; "Sur l'origine de notre système de numération," Comptes rendus, Vol. VIII, pp. 72-81; and note "Sur le passage du premier livre de la géométrie de Boèce, relatif à un nouveau système de numération," in his work Aperçu historique sur l'origine et le devéloppement des méthodes en géométrie, of which the first edition appeared in 1837.
[339] J. L. Heiberg places the book in the eleventh century on philological grounds, Philologus, loc. cit.; Woepcke, in Propagation, p. 44; Blume, Lachmann, and Rudorff, Die Schriften der römischen Feldmesser, Berlin, 1848; Boeckh, De abaco graecorum, Berlin, 1841; Friedlein, in his Leipzig edition of 1867; Weissenborn, Abhandlungen, Vol. II, p. 185, his Gerbert, pp. 1, 247, and his Geschichte der Einführung der jetzigen Ziffern in Europa durch Gerbert, Berlin, 1892, p. 11; Bayley, loc. cit., p. 59; Gerhardt, Études, p. 17, Entstehung und Ausbreitung, p. 14; Nagl, Gerbert, p. 57; Bubnov, loc. cit. See also the discussion by Chasles, Halliwell, and Libri, in the Comptes rendus, 1839, Vol. IX, p. 447, and in Vols. VIII, XVI, XVII of the same journal.
[340] J. Marquardt, La vie privée des Romains, Vol. II (French trans.), p. 505, Paris, 1893.
[341] In a Plimpton manuscript of
the arithmetic of Boethius of the thirteenth century, for example, the
Roman numerals are all replaced by the Arabic, and the same is true in
the first printed edition of the book. (See Smith's Rara
Arithmetica, pp. 434, 25-27.) D. E. Smith also copied from a
manuscript of the arithmetic in the Laurentian library at Florence, of
1370, the following forms, 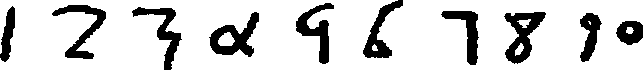 which, of course, are interpolations. An interesting
example of a forgery in ecclesiastical matters is in the charter said to
have been given by St. Patrick, granting indulgences to the benefactors
of Glastonbury, dated "In nomine domini nostri Jhesu Christi Ego
Patricius humilis servunculus Dei anno incarnationis ejusdem ccccxxx."
Now if the Benedictines are right in saying that Dionysius Exiguus, a
Scythian monk, first arranged the Christian chronology c. 532 A.D., this can hardly be other than spurious. See
Arbuthnot, loc. cit., p. 38.
which, of course, are interpolations. An interesting
example of a forgery in ecclesiastical matters is in the charter said to
have been given by St. Patrick, granting indulgences to the benefactors
of Glastonbury, dated "In nomine domini nostri Jhesu Christi Ego
Patricius humilis servunculus Dei anno incarnationis ejusdem ccccxxx."
Now if the Benedictines are right in saying that Dionysius Exiguus, a
Scythian monk, first arranged the Christian chronology c. 532 A.D., this can hardly be other than spurious. See
Arbuthnot, loc. cit., p. 38.
[342] Halliwell, in his Rara Mathematica, p. 107, states that the disputed passage is not in a manuscript belonging to Mr. Ames, nor in one at Trinity College. See also Woepcke, in Propagation, pp. 37 and 42. It was the evident corruption of the texts in such editions of Boethius as those of Venice, 1499, Basel, 1546 and 1570, that led Woepcke to publish his work Sur l'introduction de l'arithmétique indienne en Occident.
[343] They are found in none of the very ancient manuscripts, as, for example, in the ninth-century (?) codex in the Laurentian library which one of the authors has examined. It should be said, however, that the disputed passage was written after the arithmetic, for it contains a reference to that work. See the Friedlein ed., p. 397.
[344] Smith, Rara Arithmetica, p. 66.
[345] J. L. Heiberg, Philologus, Vol. XLIII, p. 507.
[346] "Nosse autem huius artis dispicientem, quid sint digiti, quid articuli, quid compositi, quid incompositi numeri." [Friedlein ed., p. 395.]
[347] De ratione abaci. In this he describes "quandam formulam, quam ob honorem sui praeceptoris mensam Pythagoream nominabant ... a posterioribus appellabatur abacus." This, as pictured in the text, is the common Gerbert abacus. In the edition in Migne's Patrologia Latina, Vol. LXIII, an ordinary multiplication table (sometimes called Pythagorean abacus) is given in the illustration.
[348] "Habebant enim diverse formatos apices vel caracteres." See the reference to Gerbert on p. 117.
[349] C. Henry, "Sur l'origine de quelques notations mathématiques," Revue Archéologique, 1879, derives these from the initial letters used as abbreviations for the names of the numerals, a theory that finds few supporters.
[350] E.g., it appears in
Schonerus, Algorithmus Demonstratus, Nürnberg, 1534, f. A4. In
England it appeared in the earliest English arithmetical manuscript
known, The Crafte of Nombrynge: "¶ fforthermore ye most
vndirstonde that in this craft ben vsid teen figurys, as here bene writen
for ensampul, 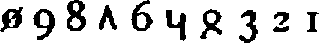 ... in the quych
we vse teen figurys of Inde. Questio. ¶ why ten fyguris of Inde? Solucio.
for as I have sayd afore thei were fonde fyrst in Inde of a kynge of that
Cuntre, that was called Algor." See Smith, An Early English
Algorism, loc. cit.
... in the quych
we vse teen figurys of Inde. Questio. ¶ why ten fyguris of Inde? Solucio.
for as I have sayd afore thei were fonde fyrst in Inde of a kynge of that
Cuntre, that was called Algor." See Smith, An Early English
Algorism, loc. cit.
[351] Friedlein ed., p. 397.
[352] Carlsruhe codex of Gerlando.
[353] Munich codex of Gerlando.
[354] Carlsruhe codex of Bernelinus.
[355] Munich codex of Bernelinus.
[356] Turchill, c. 1200.
[357] Anon. MS., thirteenth century, Alexandrian Library, Rome.
[358] Twelfth-century Boethius, Friedlein, p. 396.
[359] Vatican codex, tenth century, Boethius.
[360] a, h, i, are from the
Friedlein ed.; the original in the manuscript from which a is taken
contains a zero symbol, as do all of the six plates given by Friedlein.
b-e from the Boncompagni Bulletino, Vol. X, p. 596; f ibid., Vol.
XV, p. 186; g Memorie della classe di sci., Reale Acc. dei Lincei,
An. CCLXXIV (1876-1877), April, 1877. A twelfth-century arithmetician,
possibly John of Luna (Hispalensis, of Seville, c. 1150), speaks of the
great diversity of these forms even in his day, saying: "Est autem in
aliquibus figuram istarum apud multos diuersitas. Quidam enim septimam
hanc figuram representant 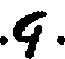 alii autem sic
alii autem sic  , uel sic
, uel sic 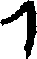 . Quidam vero
quartam sic
. Quidam vero
quartam sic  ." [Boncompagni,
Trattati, Vol. II, p. 28.]
." [Boncompagni,
Trattati, Vol. II, p. 28.]
[361] Loc. cit., p. 59.
[362] Ibid., p. 101.
[363] Loc. cit., p. 396.
[364] Khosrū I, who began to reign in 531 A.D. See W. S. W Vaux, Persia, London, 1875, p. 169; Th. Nöldeke, Aufsätze zur persichen Geschichte, Leipzig, 1887, p. 113, and his article in the ninth edition of the Encyclopædia Britannica.
[365] Colebrooke, Essays, Vol. II, p. 504, on the authority of Ibn al-Adamī, astronomer, in a work published by his continuator Al-Qāsim in 920 A.D.; Al-Bīrūnī, India, Vol. II, p. 15.
[366] H. Suter, Die Mathematiker etc., pp. 4-5, states that Al-Fazārī died between 796 and 806.
[367] Suter, loc. cit., p. 63.
[368] Suter, loc. cit., p. 74.
[369] Suter, Das Mathematiker-Verzeichniss im Fihrist. The references to Suter, unless otherwise stated, are to his later work Die Mathematiker und Astronomen der Araber etc.
[370] Suter, Fihrist, p. 37, no date.
[371] Suter, Fihrist, p. 38, no date.
[372] Possibly late tenth, since he refers to one arithmetical work which is entitled Book of the Cyphers in his Chronology, English ed., p. 132. Suter, Die Mathematiker etc., pp. 98-100, does not mention this work; see the Nachträge und Berichtigungen, pp. 170-172.
[373] Suter, pp. 96-97.
[374] Suter, p. 111.
[375] Suter, p. 124. As the name shows, he came from the West.
[376] Suter, p. 138.
[377] Hankel, Zur Geschichte der Mathematik, p. 256, refers to him as writing on the Hindu art of reckoning; Suter, p. 162.
[378] Ψηφοφορία κατ' Ἰνδούς, Greek ed., C. I. Gerhardt, Halle, 1865; and German translation, Das Rechenbuch des Maximus Planudes, H. Wäschke, Halle, 1878.
[379] "Sur une donnée historique relative à l'emploi des chiffres indiens par les Arabes," Tortolini's Annali di scienze mat. e fis., 1855.
[380] Suter, p. 80.
[381] Suter, p. 68.
[382] Sprenger also calls attention to this fact, in the Zeitschrift d. deutschen morgenländ. Gesellschaft, Vol. XLV, p. 367.
[383] Libri, Histoire des mathématiques, Vol. I, p. 147.
[384] "Dictant la paix à l'empereur de Constantinople, l'Arabe victorieux demandait des manuscrits et des savans." [Libri, loc. cit., p. 108.]
[385] Persian bagadata, "God-given."
[386] One of the Abbassides, the (at least pretended) descendants of ‛Al-Abbās, uncle and adviser of Moḥammed.
[387] E. Reclus, Asia, American ed., N. Y., 1891, Vol. IV, p. 227.
[388] Historical Sketches, Vol. III, chap. iii.
[389] On its prominence at that period see Villicus, p. 70.
[390] See pp. 4-5.
[391] Smith, D. E., in the Cantor Festschrift, 1909, note pp. 10-11. See also F. Woepcke, Propagation.
[392] Eneström, in Bibliotheca Mathematica, Vol. I (3), p. 499; Cantor, Geschichte, Vol. I (3), p. 671.
[393] Cited in Chapter I. It begins: "Dixit algoritmi: laudes deo rectori nostro atque defensori dicamus dignas." It is devoted entirely to the fundamental operations and contains no applications.
[394] M. Steinschneider, "Die Mathematik bei den Juden," Bibliotheca Mathematica, Vol. VIII (2), p. 99. See also the reference to this writer in Chapter I.
[395] Part of this work has been translated from a Leyden MS. by F. Woepcke, Propagation, and more recently by H. Suter, Bibliotheca Mathematica, Vol. VII (3), pp. 113-119.
[396] A. Neander, General History of the Christian Religion and Church, 5th American ed., Boston, 1855, Vol. III, p. 335.
[397] Beazley, loc. cit., Vol. I, p. 49.
[398] Beazley, loc. cit., Vol. I, pp. 50, 460.
[400] The name also appears as Moḥammed Abū'l-Qāsim, and Ibn Hauqal. Beazley, loc. cit., Vol. I, p. 45.
[401] Kitāb al-masālik wa'l-mamālik.
[402] Reinaud, Mém. sur l'Inde; in Gerhardt, Études, p. 18.
[403] Born at Shiraz in 1193. He himself had traveled from India to Europe.
[404] Gulistan (Rose Garden), Gateway the third, XXII. Sir Edwin Arnold's translation, N. Y., 1899, p. 177.
[405] Cunningham, loc. cit., p. 81.
[406] Putnam, Books, Vol. I, p. 227:
"Non semel externas peregrino tramite terras
Jam peragravit ovans, sophiae deductus amore,
Si quid forte novi librorum seu studiorum
Quod secum ferret, terris reperiret in illis.
Hic quoque Romuleum venit devotus ad urbem."
("More than once he has traveled joyfully through remote regions and by strange roads, led on by his zeal for knowledge and seeking to discover in foreign lands novelties in books or in studies which he could take back with him. And this zealous student journeyed to the city of Romulus.")
[407] A. Neander, General History of the Christian Religion and Church, 5th American ed., Boston, 1855, Vol. III, p. 89, note 4; Libri, Histoire, Vol. I, p. 143.
[408] Cunningham, loc. cit., p. 81.
[409] Heyd, loc. cit., Vol. I, p. 4.
[410] Ibid., p. 5.
[411] Ibid., p. 21.
[412] Ibid., p. 23.
[413] Libri, Histoire, Vol. I, p. 167.
[414] Picavet, Gerbert, un pape philosophe, d'après l'histoire et d'après la légende, Paris, 1897, p. 19.
[415] Beazley, loc. cit., Vol. I, chap, i, and p. 54 seq.
[416] Ibid., p. 57.
[417] Libri, Histoire, Vol. I, p. 110, n., citing authorities, and p. 152.
[418] Possibly the old tradition, "Prima dedit nautis usum magnetis Amalphis," is true so far as it means the modern form of compass card. See Beazley, loc. cit., Vol. II, p. 398.
[419] R. C. Dutt, loc. cit., Vol. II, p. 312.
[420] E. J. Payne, in The Cambridge Modern History, London, 1902, Vol. I, chap. i.
[421] Geo. Phillips, "The Identity of Marco Polo's Zaitun with Changchau, in T'oung pao," Archives pour servir à l'étude de l'histoire de l'Asie orientale, Leyden, 1890, Vol. I, p. 218. W. Heyd, Geschichte des Levanthandels im Mittelalter, Vol. II, p. 216.
The Palazzo dei Poli, where Marco was born and died, still stands in the Corte del Milione, in Venice. The best description of the Polo travels, and of other travels of the later Middle Ages, is found in C. R. Beazley's Dawn of Modern Geography, Vol. III, chap, ii, and Part II.
[422] Heyd, loc. cit., Vol. II, p. 220; H. Yule, in Encyclopædia Britannica, 9th (10th) or 11th ed., article "China." The handbook cited is Pegolotti's Libro di divisamenti di paesi, chapters i-ii, where it is implied that $60,000 would be a likely amount for a merchant going to China to invest in his trip.
[423] Cunningham, loc. cit., p. 194.
[424] I.e. a commission house.
[425] Cunningham, loc. cit., p. 186.
[426] J. R. Green, Short History of the English People, New York, 1890, p. 66.
[427] W. Besant, London, New York, 1892, p. 43.
[428] Baldakin, baldekin, baldachino.
[429] Italian Baldacco.
[430] J. K. Mumford, Oriental Rugs, New York, 1901, p. 18.
[431] Or Girbert, the Latin forms Gerbertus and Girbertus appearing indifferently in the documents of his time.
[432] See, for example, J. C. Heilbronner, Historia matheseos universæ, p. 740.
[433] "Obscuro loco natum," as an old chronicle of Aurillac has it.
[434] N. Bubnov, Gerberti postea Silvestri II papae opera mathematica, Berlin, 1899, is the most complete and reliable source of information; Picavet, loc. cit., Gerbert etc.; Olleris, Œuvres de Gerbert, Paris, 1867; Havet, Lettres de Gerbert, Paris, 1889 ; H. Weissenborn, Gerbert; Beiträge zur Kenntnis der Mathematik des Mittelalters, Berlin, 1888, and Zur Geschichte der Einführung der jetzigen Ziffern in Europa durch Gerbert, Berlin, 1892; Büdinger, Ueber Gerberts wissenschaftliche und politische Stellung, Cassel, 1851; Richer, "Historiarum liber III," in Bubnov, loc. cit., pp. 376-381; Nagl, Gerbert und die Rechenkunst des 10. Jahrhunderts, Vienna, 1888.
[435] Richer tells of the visit to Aurillac by Borel, a Spanish nobleman, just as Gerbert was entering into young manhood. He relates how affectionately the abbot received him, asking if there were men in Spain well versed in the arts. Upon Borel's reply in the affirmative, the abbot asked that one of his young men might accompany him upon his return, that he might carry on his studies there.
[436] Vicus Ausona. Hatto also appears as Atton and Hatton.
[437] This is all that we know of his sojourn in Spain, and this comes from his pupil Richer. The stories told by Adhemar of Chabanois, an apparently ignorant and certainly untrustworthy contemporary, of his going to Cordova, are unsupported. (See e.g. Picavet, p. 34.) Nevertheless this testimony is still accepted: K. von Raumer, for example (Geschichte der Pädagogik, 6th ed., 1890, Vol. I, p. 6), says "Mathematik studierte man im Mittelalter bei den Arabern in Spanien. Zu ihnen gieng Gerbert, nachmaliger Pabst Sylvester II."
[438] Thus in a letter to Aldaberon he says: "Quos post repperimus speretis, id est VIII volumina Boeti de astrologia, praeclarissima quoque figurarum geometriæ, aliaque non minus admiranda" (Epist. 8). Also in a letter to Rainard (Epist. 130), he says: "Ex tuis sumptibus fac ut michi scribantur M. Manlius (Manilius in one MS.) de astrologia."
[439] Picavet, loc. cit., p. 31.
[440] Picavet, loc. cit., p. 36.
[441] Havet, loc. cit., p. vii.
[442] Picavet, loc. cit., p. 37.
[443] "Con sinistre arti conseguri la dignita del Pontificato.... Lasciato poi l' abito, e 'l monasterio, e datosi tutto in potere del diavolo." [Quoted in Bombelli, L'antica numerazione Italica, Rome, 1876, p. 41 n.]
[444] He writes from Rheims in 984 to one Lupitus, in Barcelona, saying: "Itaque librum de astrologia translatum a te michi petenti dirige," presumably referring to some Arabic treatise. [Epist. no. 24 of the Havet collection, p. 19.]
[445] See Bubnov, loc. cit., p. x.
[446] Olleris, loc. cit., p. 361, l. 15, for Bernelinus; and Bubnov, loc. cit., p. 381, l. 4, for Richer.
[447] Woepcke found this in a Paris MS. of Radulph of Laon, c. 1100. [Propagation, p. 246.] "Et prima quidem trium spaciorum superductio unitatis caractere inscribitur, qui chaldeo nomine dicitur igin." See also Alfred Nagl, "Der arithmetische Tractat des Radulph von Laon" (Abhandlungen zur Geschichte der Mathematik, Vol. V, pp. 85-133), p. 97.
[448] Weissenborn, loc. cit., p. 239. When Olleris (Œuvres de Gerbert, Paris, 1867, p. cci) says, "C'est à lui et non point aux Arabes, que l'Europe doit son système et ses signes de numération," he exaggerates, since the evidence is all against his knowing the place value. Friedlein emphasizes this in the Zeitschrift für Mathematik und Physik, Vol. XII (1867), Literaturzeitung, p. 70: "Für das System unserer Numeration ist die Null das wesentlichste Merkmal, und diese kannte Gerbert nicht. Er selbst schrieb alle Zahlen mit den römischen Zahlzeichen und man kann ihm also nicht verdanken, was er selbst nicht kannte."
[449] E.g., Chasles, Büdinger, Gerhardt, and Richer. So Martin (Recherches nouvelles etc.) believes that Gerbert received them from Boethius or his followers. See Woepcke, Propagation, p. 41.
[450] Büdinger, loc. cit., p. 10. Nevertheless, in Gerbert's time one Al-Manṣūr, governing Spain under the name of Hishām (976-1002), called from the Orient Al-Beġānī to teach his son, so that scholars were recognized. [Picavet, p. 36.]
[451] Weissenborn, loc. cit., p. 235.
[452] Ibid., p. 234.
[453] These letters, of the period 983-997, were edited by Havet, loc. cit., and, less completely, by Olleris, loc. cit. Those touching mathematical topics were edited by Bubnov, loc. cit., pp. 98-106.
[454] He published it in the Monumenta Germaniae historica, "Scriptores," Vol. III, and at least three other editions have since appeared, viz. those by Guadet in 1845, by Poinsignon in 1855, and by Waitz in 1877.
[455] Domino ac beatissimo Patri Gerberto, Remorum archiepiscopo, Richerus Monchus, Gallorum congressibus in volumine regerendis, imperii tui, pater sanctissime Gerberte, auctoritas seminarium dedit.
[456] In epistle 17 (Havet collection) he speaks of the "De multiplicatione et divisione numerorum libellum a Joseph Ispano editum abbas Warnerius" (a person otherwise unknown). In epistle 25 he says: "De multiplicatione et divisione numerorum, Joseph Sapiens sententias quasdam edidit."
[457] H. Suter, "Zur Frage über den Josephus Sapiens," Bibliotheca Mathematica, Vol. VIII (2), p. 84; Weissenborn, Einführung, p. 14; also his Gerbert; M. Steinschneider, in Bibliotheca Mathematica, 1893, p. 68. Wallis (Algebra, 1685, chap. 14) went over the list of Spanish Josephs very carefully, but could find nothing save that "Josephus Hispanus seu Josephus sapiens videtur aut Maurus fuisse aut alius quis in Hispania."
[458] P. Ewald, Mittheilungen, Neues Archiv d. Gesellschaft für ältere deutsche Geschichtskunde, Vol. VIII, 1883, pp. 354-364. One of the manuscripts is of 976 A.D. and the other of 992 A.D. See also Franz Steffens, Lateinische Paläographie, Freiburg (Schweiz), 1903, pp. xxxix-xl. The forms are reproduced in the plate on page 140.
[459] It is entitled Constantino suo Gerbertus scolasticus, because it was addressed to Constantine, a monk of the Abbey of Fleury. The text of the letter to Constantine, preceding the treatise on the Abacus, is given in the Comptes rendus, Vol. XVI (1843), p. 295. This book seems to have been written c. 980 A.D. [Bubnov, loc. cit., p. 6.]
[460] "Histoire de l'Arithmétique," Comptes rendus, Vol. XVI (1843), pp. 156, 281.
[461] Loc. cit., Gerberti Opera etc.
[462] Friedlein thought it spurious. See Zeitschrift für Mathematik und Physik, Vol. XII (1867), Hist.-lit. suppl., p. 74. It was discovered in the library of the Benedictine monastry of St. Peter, at Salzburg, and was published by Peter Bernhard Pez in 1721. Doubt was first cast upon it in the Olleris edition (Œuvres de Gerbert). See Weissenborn, Gerbert, pp. 2, 6, 168, and Picavet, p. 81. Hock, Cantor, and Th. Martin place the composition of the work at c. 996 when Gerbert was in Germany, while Olleris and Picavet refer it to the period when he was at Rheims.
[463] Picavet, loc. cit., p. 182.
[464] Who wrote after Gerbert became pope, for he uses, in his preface, the words, "a domino pape Gerberto." He was quite certainly not later than the eleventh century; we do not have exact information about the time in which he lived.
[465] Picavet, loc. cit., p. 182. Weissenborn, Gerbert, p. 227. In Olleris, Liber Abaci (of Bernelinus), p. 361.
[466] Richer, in Bubnov, loc. cit., p. 381.
[467] Weissenborn, Gerbert, p. 241.
[468] Writers on numismatics are quite uncertain as to their use. See F. Gnecchi, Monete Romane, 2d ed., Milan, 1900, cap. XXXVII. For pictures of old Greek tesserae of Sarmatia, see S. Ambrosoli, Monete Greche, Milan, 1899, p. 202.
[469] Thus Tzwivel's arithmetic of 1507, fol. 2, v., speaks of the ten figures as "characteres sive numerorum apices a diuo Seuerino Boetio."
[470] Weissenborn uses sipos for 0. It is not given by Bernelinus, and appears in Radulph of Laon, in the twelfth century. See Günther's Geschichte, p. 98, n.; Weissenborn, p. 11; Pihan, Exposé etc., pp. xvi-xxii.
In Friedlein's Boetius, p. 396, the plate shows that all of the six important manuscripts from which the illustrations are taken contain the symbol, while four out of five which give the words use the word sipos for 0. The names appear in a twelfth-century anonymous manuscript in the Vatican, in a passage beginning
Ordine primigeno sibi nomen possidet igin.
Andras ecce locum mox uendicat ipse secundum
Ormis post numeros incompositus sibi primus.
[Boncompagni Buttetino, XV, p. 132.] Turchill (twelfth century) gives the names Igin, andras, hormis, arbas, quimas, caletis, zenis, temenias, celentis, saying: "Has autem figuras, ut donnus [dominus] Gvillelmus Rx testatur, a pytagoricis habemus, nomina uero ab arabibus." (Who the William R. was is not known. Boncompagni Bulletino XV, p. 136.) Radulph of Laon (d. 1131) asserted that they were Chaldean (Propagation, p. 48 n.). A discussion of the whole question is also given in E. C. Bayley, loc. cit. Huet, writing in 1679, asserted that they were of Semitic origin, as did Nesselmann in spite of his despair over ormis, calctis, and celentis; see Woepcke, Propagation, p. 48. The names were used as late as the fifteenth century, without the zero, but with the superscript dot for 10's, two dots for 100's, etc., as among the early Arabs. Gerhardt mentions having seen a fourteenth or fifteenth century manuscript in the Bibliotheca Amploniana with the names "Ingnin, andras, armis, arbas, quinas, calctis, zencis, zemenias, zcelentis," and the statement "Si unum punctum super ingnin ponitur, X significat.... Si duo puncta super ... figuras superponunter, fiet decuplim illius quod cum uno puncto significabatur," in Monatsberichte der K. P. Akad. d. Wiss., Berlin, 1867, p. 40.
[471] A chart of ten numerals in 200 tongues, by Rev. R. Patrick, London, 1812.
[472] "Numeratio figuralis est cuiusuis numeri per notas, et figuras numerates descriptio." [Clichtoveus, edition of c. 1507, fol. C ii, v.] "Aristoteles enim uoces rerum σύμβολα uocat: id translatum, sonat notas." [Noviomagus, De Numeris Libri II, cap. vi.] "Alphabetum decem notarum." [Schonerus, notes to Ramus, 1586, p. 3 seq.] Richer says: "novem numero notas omnem numerum significantes." [Bubnov, loc. cit., p. 381.]
[473] "Il y a dix Characteres, autrement Figures, Notes, ou Elements." [Peletier, edition of 1607, p. 13.] "Numerorum notas alij figuras, alij signa, alij characteres uocant." [Glareanus, 1545 edition, f. 9, r.] "Per figuras (quas zyphras uocant) assignationem, quales sunt hæ notulæ, 1. 2. 3. 4...." [Noviomagus, De Numeris Libri II, cap. vi.] Gemma Frisius also uses elementa and Cardan uses literae. In the first arithmetic by an American (Greenwood, 1729) the author speaks of "a few Arabian Charecters or Numeral Figures, called Digits" (p. 1), and as late as 1790, in the third edition of J. J. Blassière's arithmetic (1st ed. 1769), the name characters is still in use, both for "de Latynsche en de Arabische" (p. 4), as is also the term "Cyfferletters" (p. 6, n.). Ziffer, the modern German form of cipher, was commonly used to designate any of the nine figures, as by Boeschenstein and Riese, although others, like Köbel, used it only for the zero. So zifre appears in the arithmetic by Borgo, 1550 ed. In a Munich codex of the twelfth century, attributed to Gerland, they are called characters only: "Usque ad VIIII. enim porrigitur omnis numerus et qui supercrescit eisdem designator Karacteribus." [Boncompagni Bulletino, Vol. X. p. 607.]
[474] The title of his work is Prologus N. Ocreati in Helceph (Arabic al-qeif, investigation or memoir) ad Adelardum Batensem magistrum suum. The work was made known by C. Henry, in the Zeitschrift für Mathematik und Physik, Vol. XXV, p. 129, and in the Abhandlungen zur Geschichte der Mathematik, Vol. III; Weissenborn, Gerbert, p. 188.
[475] The zero is indicated by a vacant column.
[476] Leo Jordan, loc. cit., p. 170. "Chifre en augorisme" is the expression used, while a century later "giffre en argorisme" and "cyffres d'augorisme" are similarly used.
[477] The Works of Geoffrey Chaucer, edited by W. W. Skeat, Vol. IV, Oxford, 1894, p. 92.
[478] Loc. cit., Vol. III, pp. 179 and 180.
[479] In Book II, chap, vii, of The Testament of Love, printed with Chaucer's Works, loc. cit., Vol. VII, London, 1897.
[480] Liber Abacci, published in Olleris, Œuvres de Gerbert, pp. 357-400.
[481] G. R. Kaye, "The Use of the Abacus in Ancient India," Journal and Proceedings of the Asiatic Society of Bengal, 1908, pp. 293-297.
[482] Liber Abbaci, by Leonardo Pisano, loc. cit., p. 1.
[483] Friedlein, "Die Entwickelung des Rechnens mit Columnen," Zeitschrift für Mathematik und Physik, Vol. X, p. 247.
[484] The divisor 6 or 16 being increased by the difference 4, to 10 or 20 respectively.
[485] E.g. Cantor, Vol. I, p. 882.
[486] Friedlein, loc. cit.; Friedlein, "Gerbert's Regeln der Division" and "Das Rechnen mit Columnen vor dem 10. Jahrhundert," Zeitschrift für Mathematik und Physik, Vol. IX; Bubnov, loc. cit., pp. 197-245; M. Chasles, "Histoire de l'arithmétique. Recherches des traces du système de l'abacus, après que cette méthode a pris le nom d'Algorisme.—Preuves qu'à toutes les époques, jusq'au XVIe siècle, on a su que l'arithmétique vulgaire avait pour origine cette méthode ancienne," Comptes rendus, Vol. XVII, pp. 143-154, also "Règles de l'abacus," Comptes rendus, Vol. XVI, pp. 218-246, and "Analyse et explication du traité de Gerbert," Comptes rendus, Vol. XVI, pp. 281-299.
[487] Bubnov, loc. cit., pp. 203-204, "Abbonis abacus."
[488] "Regulae de numerorum abaci rationibus," in Bubnov, loc. cit., pp. 205-225.
[489] P. Treutlein, "Intorno ad alcuni scritti inediti relativi al calcolo dell' abaco," Bulletino di bibliografia e di storia delle scienze matematiche e fisiche, Vol. X, pp. 589-647.
[490] "Intorno ad uno scritto inedito di Adelhardo di Bath intitolato 'Regulae Abaci,'" B. Boncompagni, in his Bulletino, Vol. XIV, pp. 1-134.
[491] Treutlein, loc. cit.; Boncompagni, "Intorno al Tractatus de Abaco di Gerlando," Bulletino, Vol. X, pp. 648-656.
[492] E. Narducci, "Intorno a due trattati inediti d'abaco contenuti in due codici Vaticani del secolo XII," Boncompagni Bulletino, Vol. XV, pp. 111-162.
[493] See Molinier, Les sources de l'histoire de France, Vol. II, Paris, 1902, pp. 2, 3.
[494] Cantor, Geschichte, Vol. I, p. 762. A. Nagl in the Abhandlungen zur Geschichte der Mathematik, Vol. V, p. 85.
[495] 1030-1117.
[496] Abhandlungen zur Geschichte der Mathematik, Vol. V, pp. 85-133. The work begins "Incipit Liber Radulfi laudunensis de abaco."
[497] Materialien zur Geschichte der arabischen Zahlzeichen in Frankreich, loc. cit.
[498] Who died in 1202.
[499] Cantor, Geschichte, Vol. I (3), pp. 800-803; Boncompagni, Trattati, Part II. M. Steinschneider ("Die Mathematik bei den Juden," Bibliotheca Mathematica, Vol. X (2), p. 79) ingeniously derives another name by which he is called (Abendeuth) from Ibn Daūd (Son of David). See also Abhandlungen, Vol. III, p. 110.
[500] John is said to have died in 1157.
[501] For it says, "Incipit prologus in libro alghoarismi de practica arismetrice. Qui editus est a magistro Johanne yspalensi." It is published in full in the second part of Boncompagni's Trattati d'aritmetica.
[502] Possibly, indeed, the meaning of "libro alghoarismi" is not "to Al-Khowārazmī's book," but "to a book of algorism." John of Luna says of it: "Hoc idem est illud etiam quod ... alcorismus dicere videtur." [Trattati, p. 68.]
[503] For a résumé, see Cantor, Vol. I (3), pp. 800-803. As to the author, see Eneström in the Bibliotheca Mathematica, Vol. VI (3), p. 114, and Vol. IX (3), p. 2.
[504] Born at Cremona (although some have asserted at Carmona, in Andalusia) in 1114; died at Toledo in 1187. Cantor, loc. cit.; Boncompagni, Atti d. R. Accad. d. n. Lincei, 1851.
[505] See Abhandlungen zur Geschichte der Mathematik, Vol. XIV, p. 149; Bibliotheca Mathematica, Vol. IV (3), p. 206. Boncompagni had a fourteenth-century manuscript of his work, Gerardi Cremonensis artis metrice practice. See also T. L. Heath, The Thirteen Books of Euclid's Elements, 3 vols., Cambridge, 1908, Vol. I, pp. 92-94 ; A. A. Björnbo, "Gerhard von Cremonas Übersetzung von Alkwarizmis Algebra und von Euklids Elementen," Bibliotheca Mathematica, Vol. VI (3), pp. 239-248.
[506] Wallis, Algebra, 1685, p. 12 seq.
[507] Cantor, Geschichte, Vol. I (3), p. 906; A. A. Björnbo, "Al-Chwārizmī's trigonometriske Tavler," Festskrift til H. G. Zeuthen, Copenhagen, 1909, pp. 1-17.
[508] Heath, loc. cit., pp. 93-96.
[509] M. Steinschneider, Zeitschrift der deutschen morgenländischen Gesellschaft, Vol. XXV, 1871, p. 104, and Zeitschrift für Mathematik und Physik, Vol. XVI, 1871, pp. 392-393; M. Curtze, Centralblatt für Bibliothekswesen, 1899, p. 289; E. Wappler, Zur Geschichte der deutschen Algebra im 15. Jahrhundert, Programm, Zwickau, 1887; L. C. Karpinski, "Robert of Chester's Translation of the Algebra of Al-Khowārazmī," Bibliotheca Mathematica, Vol. XI (3), p. 125. He is also known as Robertus Retinensis, or Robert of Reading.
[510] Nagl, A., "Ueber eine Algorismus-Schrift des XII. Jahrhunderts und über die Verbreitung der indisch-arabischen Rechenkunst und Zahlzeichen im christl. Abendlande," in the Zeitschrift für Mathematik und Physik, Hist.-lit. Abth., Vol. XXXIV, p. 129. Curtze, Abhandlungen zur Geschichte der Mathematik, Vol. VIII, pp. 1-27.
[511] See line a in the plate on p. 143.
[512] Sefer ha-Mispar, Das Buch der Zahl, ein hebräisch-arithmetisches Werk des R. Abraham ibn Esra, Moritz Silberberg, Frankfurt a. M., 1895.
[513] Browning's "Rabbi ben Ezra."
[514] "Darum haben auch die Weisen Indiens all ihre Zahlen durch neun bezeichnet und Formen für die 9 Ziffern gebildet." [Sefer ha-Mispar, loc. cit., p. 2.]
[515] F. Bonaini, "Memoria unica sincrona di Leonardo Fibonacci," Pisa, 1858, republished in 1867, and appearing in the Giornale Arcadico, Vol. CXCVII (N.S. LII); Gaetano Milanesi, Documento inedito e sconosciuto a Lionardo Fibonacci, Roma, 1867; Guglielmini, Elogio di Lionardo Pisano, Bologna, 1812, p. 35; Libri, Histoire des sciences mathématiques, Vol. II, p. 25; D. Martines, Origine e progressi dell' aritmetica, Messina, 1865, p. 47; Lucas, in Boncompagni Bulletino, Vol. X, pp. 129, 239; Besagne, ibid., Vol. IX, p. 583; Boncompagni, three works as cited in Chap. I; G. Eneström, "Ueber zwei angebliche mathematische Schulen im christlichen Mittelalter," Bibliotheca Mathematica, Vol. VIII (3), pp. 252-262; Boncompagni, "Della vita e delle opere di Leonardo Pisano," loc. cit.
[516] The date is purely conjectural. See the Bibliotheca Mathematica, Vol. IV (3), p. 215.
[517] An old chronicle relates that in 1063 Pisa fought a great battle with the Saracens at Palermo, capturing six ships, one being "full of wondrous treasure," and this was devoted to building the cathedral.
[518] Heyd, loc. cit., Vol. I, p. 149.
[519] Ibid., p. 211.
[520] J. A. Symonds, Renaissance in Italy. The Age of Despots. New York, 1883, p. 62.
[521] Symonds, loc. cit., p. 79.
[522] J. A. Froude, The Science of History, London, 1864. "Un brevet d'apothicaire n'empêcha pas Dante d'être le plus grand poète de l'Italie, et ce fut un petit marchand de Pise qui donna l'algèbre aux Chrétiens." [Libri, Histoire, Vol. I, p. xvi.]
[523] A document of 1226, found and published in 1858, reads: "Leonardo bigollo quondam Guilielmi."
[524] "Bonaccingo germano suo."
[525] E.g. Libri, Guglielmini, Tiraboschi.
[526] Latin, Bonaccius.
[527] Boncompagni and Milanesi.
[528] Reprint, p. 5.
[529] Whence the French name for candle.
[530] Now part of Algiers.
[531] E. Reclus, Africa, New York, 1893, Vol. II, p. 253.
[532] "Sed hoc totum et algorismum atque arcus pictagore quasi errorem computavi respectu modi indorum." Woepcke, Propagation etc., regards this as referring to two different systems, but the expression may very well mean algorism as performed upon the Pythagorean arcs (or table).
[533] "Book of the Abacus," this term then being used, and long afterwards in Italy, to mean merely the arithmetic of computation.
[534] "Incipit liber Abaci a Leonardo filio Bonacci compositus anno 1202 et correctus ab eodem anno 1228." Three MSS. of the thirteenth century are known, viz. at Milan, at Siena, and in the Vatican library. The work was first printed by Boncompagni in 1857.
[535] I.e. in relation to the quadrivium. "Non legant in festivis diebus, nisi Philosophos et rhetoricas et quadrivalia et barbarismum et ethicam, si placet." Suter, Die Mathematik auf den Universitäten des Mittelalters, Zürich, 1887, p. 56. Roger Bacon gives a still more gloomy view of Oxford in his time in his Opus minus, in the Rerum Britannicarum medii aevi scriptores, London, 1859, Vol. I, p. 327. For a picture of Cambridge at this time consult F. W. Newman, The English Universities, translated from the German of V. A. Huber, London, 1843, Vol. I, p. 61; W. W. R. Ball, History of Mathematics at Cambridge, 1889; S. Günther, Geschichte des mathematischen Unterrichts im deutschen Mittelalter bis zum Jahre 1525, Berlin, 1887, being Vol. III of Monumenta Germaniae paedagogica.
[536] On the commercial activity of the period, it is known that bills of exchange passed between Messina and Constantinople in 1161, and that a bank was founded at Venice in 1170, the Bank of San Marco being established in the following year. The activity of Pisa was very manifest at this time. Heyd, loc. cit., Vol. II, p. 5; V. Casagrandi, Storia e cronologia, 3d ed., Milan, 1901, p. 56.
[537] J. A. Symonds, loc. cit., Vol. II, p. 127.
[538] I. Taylor, The Alphabet, London, 1883, Vol. II, p. 263.
[539] Cited by Unger's History, p. 15. The Arabic numerals appear in a Regensburg chronicle of 1167 and in Silesia in 1340. See Schmidt's Encyclopädie der Erziehung, Vol. VI, p. 726; A. Kuckuk, "Die Rechenkunst im sechzehnten Jahrhundert," Festschrift zur dritten Säcularfeier des Berlinischen Gymnasiums zum grauen Kloster, Berlin, 1874, p. 4.
[540] The text is given in Halliwell, Rara Mathematica, London, 1839.
[541] Seven are given in Ashmole's Catalogue of Manuscripts in the Oxford Library, 1845.
[542] Maximilian Curtze, Petri Philomeni de Dacia in Algorismum Vulgarem Johannis de Sacrobosco commentarius, una cum Algorismo ipso, Copenhagen, 1897; L. C. Karpinski, "Jordanus Nemorarius and John of Halifax," American Mathematical Monthly, Vol. XVII, pp. 108-113.
[543] J. Aschbach, Geschichte der Wiener Universität im ersten Jahrhunderte ihres Bestehens, Wien, 1865, p. 93.
[544] Curtze, loc. cit., gives the text.
[545] Curtze, loc. cit., found some forty-five copies of the Algorismus in three libraries of Munich, Venice, and Erfurt (Amploniana). Examination of two manuscripts from the Plimpton collection and the Columbia library shows such marked divergence from each other and from the text published by Curtze that the conclusion seems legitimate that these were students' lecture notes. The shorthand character of the writing further confirms this view, as it shows that they were written largely for the personal use of the writers.
[546] "Quidam philosophus edidit nomine Algus, unde et Algorismus nuncupatur." [Curtze, loc. cit., p. 1.]
[547] "Sinistrorsum autera scribimus in hac arte more arabico sive iudaico, huius scientiae inventorum." [Curtze, loc. cit., p. 7.] The Plimpton manuscript omits the words "sive iudaico."
[548] "Non enim omnis numerus per quascumque figuras Indorum repraesentatur, sed tantum determinatus per determinatam, ut 4 non per 5,..." [Curtze, loc. cit., p. 25.]
[549] C. Henry, "Sur les deux plus anciens traités français d'algorisme et de géométrie," Boncompagni Bulletino, Vol. XV, p. 49; Victor Mortet, "Le plus ancien traité français d'algorisme," loc. cit.
[550] L'État des sciences en France, depute la mort du Roy Robert, arrivée en 1031, jusqu'à celle de Philippe le Bel, arrivée en 1314, Paris, 1741.
[551] Discours sur l'état des lettres en France au XIIIe siecle, Paris, 1824.
[552] Aperçu historique, Paris, 1876 ed., p. 464.
[553] Ranulf Higden, a native of the west of England, entered St. Werburgh's monastery at Chester in 1299. He was a Benedictine monk and chronicler, and died in 1364. His Polychronicon, a history in seven books, was printed by Caxton in 1480.
[554] Trevisa's translation, Higden having written in Latin.
[555] An illustration of this feeling is seen in the writings of Prosdocimo de' Beldomandi (b. c. 1370-1380, d. 1428): "Inveni in quam pluribus libris algorismi nuncupatis mores circa numeros operandi satis varios atque diversos, qui licet boni existerent atque veri erant, tamen fastidiosi, tum propter ipsarum regularum multitudinem, tum propter earum deleationes, tum etiam propter ipsarum operationum probationes, utrum si bone fuerint vel ne. Erant et etiam isti modi interim fastidiosi, quod si in aliquo calculo astroloico error contigisset, calculatorem operationem suam a capite incipere oportebat, dato quod error suus adhuc satis propinquus existeret; et hoc propter figuras in sua operatione deletas. Indigebat etiam calculator semper aliquo lapide vel sibi conformi, super quo scribere atque faciliter delere posset figuras cum quibus operabatur in calculo suo. Et quia haec omnia satis fastidiosa atque laboriosa mihi visa sunt, disposui libellum edere in quo omnia ista abicerentur: qui etiam algorismus sive liber de numeris denominari poterit. Scias tamen quod in hoc libello ponere non intendo nisi ea quae ad calculum necessaria sunt, alia quae in aliis libris practice arismetrice tanguntur, ad calculum non necessaria, propter brevitatem dimitendo." [Quoted by A. Nagl, Zeitschrift für Mathematik und Physik, Hist.-lit. Abth., Vol. XXXIV, p. 143; Smith, Rara Arithmetica, p. 14, in facsimile.]
[556] P. Ewald, loc. cit.; Franz Steffens, Lateinische Paläographie, pp. xxxix-xl. We are indebted to Professor J. M. Burnam for a photograph of this rare manuscript.
[557] See the plate of forms on p. 88.
[558] Karabacek, loc. cit., p. 56; Karpinski, "Hindu Numerals in the Fihrist," Bibliotheca Mathematica, Vol. XI (3), p. 121.
[559] Woepcke, "Sur une donnée historique," etc., loc. cit., and "Essai d'une restitution de travaux perdus d'Apollonius sur les quantités irrationnelles, d'après des indications tirées d'un manuscrit arabe," Tome XIV des Mémoires présentés par divers savants à l'Académie des sciences, Paris, 1856, note, pp. 6-14.
[560] Archeological Report of the Egypt Exploration Fund for 1908-1909, London, 1910, p. 18.
[561] There was a set of astronomical tables in Boncompagni's library bearing this date: "Nota quod anno dni nri ihû xpi. 1264. perfecto." See Narducci's Catalogo, p. 130.
[562] "On the Early use of Arabic Numerals in Europe," read before the Society of Antiquaries April 14, 1910, and published in Archæologia in the same year.
[563] Ibid., p. 8, n. The date is part of an Arabic inscription.
[564] O. Codrington, A Manual of Musalman Numismatics, London, 1904.
[565] See Arbuthnot, The Mysteries of Chronology, London, 1900, pp. 75, 78, 98; F. Pichler, Repertorium der steierischen Münzkunde, Grätz, 1875, where the claim is made of an Austrian coin of 1458; Bibliotheca Mathematica, Vol. X (2), p. 120, and Vol. XII (2), p. 120. There is a Brabant piece of 1478 in the collection of D. E. Smith.
[566] A specimen is in the British Museum. [Arbuthnot, p. 79.]
[567] Ibid., p. 79.
[568] Liber de Remediis utriusque fortunae Coloniae.
[569] Fr. Walthern et Hans Hurning, Nördlingen.
[570] Ars Memorandi, one of the oldest European block-books.
[571] Eusebius Caesariensis, De praeparatione evangelica, Venice, Jenson, 1470. The above statement holds for copies in the Astor Library and in the Harvard University Library.
[572] Francisco de Retza, Comestorium vitiorum, Nürnberg, 1470. The copy referred to is in the Astor Library.
[573] See Mauch, "Ueber den Gebrauch arabischer Ziffern und die Veränderungen derselben," Anzeiger für Kunde der deutschen Vorzeit, 1861, columns 46, 81, 116, 151, 189, 229, and 268; Calmet, Recherches sur l'origine des chiffres d'arithmétique, plate, loc. cit.
[574] Günther, Geschichte, p. 175, n.; Mauch, loc. cit.
[575] These are given by W. R. Lethaby, from drawings by J. T. Irvine, in the Proceedings of the Society of Antiquaries, 1906, p. 200.
[576] There are some ill-tabulated forms to be found in J. Bowring, The Decimal System, London, 1854, pp. 23, 25, and in L. A. Chassant, Dictionnaire des abréviations latines et françaises ... du moyen âge, Paris, MDCCCLXVI, p. 113. The best sources we have at present, aside from the Hill monograph, are P. Treutlein, Geschichte unserer Zahlzeichen, Karlsruhe, 1875; Cantor's Geschichte, Vol. I, table; M. Prou, Manuel de paléographie latine et française, 2d ed., Paris, 1892, p. 164; A. Cappelli, Dizionario di abbreviature latine ed italiane, Milan, 1899. An interesting early source is found in the rare Caxton work of 1480, The Myrrour of the World. In Chap. X is a cut with the various numerals, the chapter beginning "The fourth scyence is called arsmetrique." Two of the fifteen extant copies of this work are at present in the library of Mr. J. P. Morgan, in New York.
[577] From the twelfth-century manuscript on arithmetic, Curtze, loc. cit., Abhandlungen, and Nagl, loc. cit. The forms are copied from Plate VII in Zeitschrift für Mathematik und Physik, Vol. XXXIV.
[578] From the Regensburg chronicle. Plate containing some of these numerals in Monumenta Germaniae historica, "Scriptores" Vol. XVII, plate to p. 184; Wattenbach, Anleitung zur lateinischen Palaeographie, Leipzig, 1886, p. 102; Boehmer, Fontes rerum Germanicarum, Vol. III, Stuttgart, 1852, p. lxv.
[579] French Algorismus of 1275; from an unpublished photograph of the original, in the possession of D. E. Smith. See also p. 135.
[580] From a manuscript of Boethius c. 1294, in Mr. Plimpton's library. Smith, Rara Arithmetica, Plate I.
[581] Numerals in a 1303 manuscript in Sigmaringen, copied from Wattenbach, loc. cit., p. 102.
[582] From a manuscript, Add. Manuscript 27,589, British Museum, 1360 A.D. The work is a computus in which the date 1360 appears, assigned in the British Museum catalogue to the thirteenth century.
[583] From the copy of Sacrabosco's Algorismus in Mr. Plimpton's library. Date c. 1442. See Smith, Rara Arithmetica, p. 450.
[584] See Rara Arithmetica, pp. 446-447.
[585] Ibid., pp. 469-470.
[586] Ibid., pp. 477-478.
[587] The i is used for "one" in the Treviso arithmetic (1478), Clichtoveus (c. 1507 ed., where both i and j are so used), Chiarini (1481), Sacrobosco (1488 ed.), and Tzwivel (1507 ed., where jj and jz are used for 11 and 12). This was not universal, however, for the Algorithmus linealis of c. 1488 has a special type for 1. In a student's notebook of lectures taken at the University of Würzburg in 1660, in Mr. Plimpton's library, the ones are all in the form of i.
[588] Thus the date  , for 1580, appears in a MS.
in the Laurentian library at Florence. The second and the following five
characters are taken from Cappelli's Dizionario, p. 380, and are
from manuscripts of the twelfth, thirteenth, fourteenth, sixteenth,
seventeenth, and eighteenth centuries, respectively.
, for 1580, appears in a MS.
in the Laurentian library at Florence. The second and the following five
characters are taken from Cappelli's Dizionario, p. 380, and are
from manuscripts of the twelfth, thirteenth, fourteenth, sixteenth,
seventeenth, and eighteenth centuries, respectively.
[589] E.g. Chiarini's work of 1481; Clichtoveus (c. 1507).
[590] The first is from an algorismus of the thirteenth century, in the Hannover Library. [See Gerhardt, "Ueber die Entstehung und Ausbreitung des dekadischen Zahlensystems," loc. cit., p. 28.] The second character is from a French algorismus, c. 1275. [Boncompagni Bulletino, Vol. XV, p. 51.] The third and the following sixteen characters are given by Cappelli, loc. cit., and are from manuscripts of the twelfth (1), thirteenth (2), fourteenth (7), fifteenth (3), sixteenth (1), seventeenth (2), and eighteenth (1) centuries, respectively.
[591] Thus Chiarini (1481) has  for 23.
for 23.
[592] The first of these is from a French algorismus, c. 1275. The second and the following eight characters are given by Cappelli, loc. cit., and are from manuscripts of the twelfth (2), thirteenth, fourteenth, fifteenth (3), seventeenth, and eighteenth centuries, respectively.
[593] See Nagl, loc. cit.
[594] Hannover algorismus, thirteenth century.
[595] See the Dagomari manuscript, in Rara Arithmetica, pp. 435, 437-440.
[596] But in the woodcuts of the Margarita Philosophica (1503) the old forms are used, although the new ones appear in the text. In Caxton's Myrrour of the World (1480) the old form is used.
[597] Cappelli, loc. cit. They are partly from manuscripts of the tenth, twelfth, thirteenth (3), fourteenth (7), fifteenth (6), and eighteenth centuries, respectively. Those in the third line are from Chassant's Dictionnaire, p. 113, without mention of dates.
[598] The first is from the Hannover algorismus, thirteenth century. The second is taken from the Rollandus manuscript, 1424. The others in the first two lines are from Cappelli, twelfth (3), fourteenth (6), fifteenth (13) centuries, respectively. The third line is from Chassant, loc. cit., p. 113, no mention of dates.
[599] The first of these forms is from the Hannover algorismus, thirteenth century. The following are from Cappelli, fourteenth (3), fifteenth, sixteenth (2), and eighteenth centuries, respectively.
[600] The first of these is taken from the Hannover algorismus, thirteenth century. The following forms are from Cappelli, twelfth, thirteenth, fourteenth (5), fifteenth (2), seventeenth, and eighteenth centuries, respectively.
[601] All of these are given by Cappelli, thirteenth, fourteenth, fifteenth (2), and sixteenth centuries, respectively.
[602] Smith, Rara Arithmetica, p. 489. This is also seen in several of the Plimpton manuscripts, as in one written at Ancona in 1684. See also Cappelli, loc. cit.
[603] French algorismus, c. 1275,
for the first of these forms. Cappelli, thirteenth, fourteenth, fifteenth
(3), and seventeenth centuries, respectively. The last three are taken
from Byzantinische Analekten, J. L. Heiberg, being forms of the
fifteenth century, but not at all common.  was the old Greek symbol for 90.
was the old Greek symbol for 90.
[604] For the first of these the reader is referred to the forms ascribed to Boethius, in the illustration on p. 88; for the second, to Radulph of Laon, see p. 60. The third is used occasionally in the Rollandus (1424) manuscript, in Mr. Plimpton's library. The remaining three are from Cappelli, fourteenth (2) and seventeenth centuries.
[605] Smith, An Early English Algorism.
[606] Kuckuck, p. 5.
[607] A. Cappelli, loc. cit., p. 372.
[608] Smith, Rara Arithmetica, p. 443.
[609] Curtze, Petri Philomeni de Dacia etc., p. IX.
[610] Cappelli, loc. cit., p. 376.
[611] Curtze, loc. cit., pp. VIII-IX, note.
[612] Edition of 1544-1545, f. 52.
[613] De numeris libri II, 1544 ed., cap. XV. Heilbronner, loc. cit., p. 736, also gives them, and compares this with other systems.
[614] Noviomagus says of them: "De quibusdam Astrologicis, sive Chaldaicis numerorum notis.... Sunt & aliæ quædam notæ, quibus Chaldaei & Astrologii quemlibet numerum artificiose & arguté describunt, scitu periucundae, quas nobis communicauit Rodolphus Paludanus Nouiomagus."