The Project Gutenberg eBook of Lehrbuch der Perspective, by G. Conz.

Wer das Schaffen unserer Künstler kennt, der weiss, dass auch der Talentvollste nicht ohne gewissenhaftes und gründliches Studium zum Ziele gelangt, und dass sie Mühe und Arbeit nicht zu scheuen pflegen. Woher kommt es nun, dass die Mehrzahl der Maler so wenig von der Perspective versteht, welche doch zweifellos eine so wichtige Grundlage ihrer Studien bildet? Die Meisten unterschäzen den Wert derselben nicht, nehmen auch wohl dieses oder jenes Lehrbuch zur Hand, aber gewöhnlich nur, um es bald wieder zur Seite zu legen, ohne ihren Zweck erreicht zu haben, und wenn man nach dem Grunde fragt, so heisst es, das möge alles ganz gut für Architekten sein, eigne sich aber nicht für Maler.

Allerdings ist die Art und Weise, in welcher der Architekt die perspectivischen Geseze anwendet, wesentlich verschieden von der des Malers und es mag wohl sein, dass die meisten perspectivischen Lehrbücher dem Standpunkt des Lezteren weniger als dem des Ersteren Rechnung tragen.

Der Architekt stellt sich die Aufgabe, das perspectivische Bild eines Gegenstands mathematisch genau zu berechnen auf Grund bestimmter Angaben über die wirkliche (geometrische) Richtung, Grösse und Winkelstellung sämtlicher Linien, wie sie ihm in seinem Grundriss und Aufriss vorliegen. Für den Maler dagegen ist das perspectivische Bild, welches in der Natur oder in seiner Fantasie vor ihm steht, das zuerst Gegebene. In den meisten Fällen ist er darauf angewiesen, zunächst die perspectivische Richtung und Grösse einzelner für die beabsichtigte Wirkung seines Bildes wesentlicher Linien, so gut die Übung seines Auges gestattet, festzustellen und dann erst die perspectivische Berechnung anzuwenden, um das Übrige mit jenen in richtige Übereinstimmung zu bringen. Für diese Berechnung fehlen ihm aber, da er selten in der Lage ist, Messungen an seinem Gegenstand vorzunehmen, die genauen und bestimmten Angaben, welche dem Architekten zu Gebote stehen, und welche die Auffassung auch eines geübten Auges nicht vollständig ersezen kann. Er muss daher in der Regel auf eine vollständige perspectivische Genauigkeit aller Teile seines Bildes verzichten und er bezweckt eine solche auch nicht. Man kann sagen, dass er in dieser Beziehung seiner Aufgabe genügt, wenn er perspectivische Fehler vermeidet, welche für das Auge eines kundigen Beschauers ohne Anwendung einer Berechnung wahrnehmbar und deshalb für die Wirkung des Ganzen störend wären.

Hieraus ergeben sich einerseits gewisse Schwierigkeiten, welche ein für die Zwecke des Malers geeignetes Lehrbuch der Perspective zu berücksichtigen hat, anderseits bietet sich[V] die Möglichkeit, in mancher Beziehung den Stoff zu vereinfachen und leichter verständlich zu machen.

Der Umgang mit Kunstgenossen, sowie eine langjährige Lehrthätigkeit haben dem Verfasser das Bedürfnis eines in dem erwähnten Sinne geschriebenen Lehrbuchs so oft nahe gelegt und ihm zugleich so vielfache Gelegenheit gegeben, die Mittel und Wege, welche sich hiebei darbieten, zu erproben, dass er vielleicht hoffen darf, mit dieser Schrift Vielen einen Dienst zu erweisen. Neben den Bedürfnissen des Malers sind zugleich diejenigen des Schulunterrichts ins Auge gefasst. Mit Rücksicht auf diesen sind auch die einfachen geometrischen Begriffe, welche in Betracht kommen, besprochen und ist die Anordnung des Stoffes eine solche, dass die für das Freihandzeichnen wichtigsten und unentbehrlichsten Lehrsäze, welche zugleich die verständlichsten sind, leicht von den schwierigeren Teilen getrennt vorgenommen werden können.1

Auch für den Künstler haben ohne Zweifel die weniger schwierigen Berechnungen, welche sich im Notfall mittels einiger aus freier Hand gezeichneter Hilfslinien ausführen lassen, den meisten Wert und Manchen wäre vielleicht eine noch kürzere und einfachere Fassung des Ganzen erwünscht und genügend gewesen. Aber abgesehen davon, dass ein grösserer Massstab des Bildes zuweilen genauere und ausführlichere[VI] Constructionen erfordert, haben dieselben auch den Wert, das Verständnis zu üben und zu schärfen, wie überhaupt der wichtigste Nuzen solcher Studien darin besteht, dass das Auge richtiger sehen und auch ohne Anwendung einer Berechnung die Formen der Natur rascher und sicherer auffassen lernt.

Inhalt.

I. Geometrische Begriffe.

Gerade Linien.

§ 1. Eine gerade Linie ist senkrecht, wenn sie die durch das Lot oder Senkblei angegebene Richtung hat, wagrecht, wenn ihre beiden Endpunkte (und somit alle Punkte derselben) in gleicher Höhe liegen, schräg, wenn sie nach irgend einer Richtung hin steigt oder fällt. Dies gilt sowohl von den wirklichen Linien im Raume, als von den Linien einer Zeichnung, wenn wir uns leztere senkrecht stehend denken.

Linien, welche dieselbe Richtung haben, so dass der Abstand zwischen ihnen, soweit man sie verlängern mag, überall gleich gross ist, heissen Parallellinien, vgl. A B und C D, E F und G H Fig. 1. Zieht man zwischen 2 parallelen Linien Verbindungslinien, welche unter sich gleichfalls parallel sind, so sind leztere gleich lang, vgl. die Linien a, b, c, d, e, f Fig. 1.

Winkel.

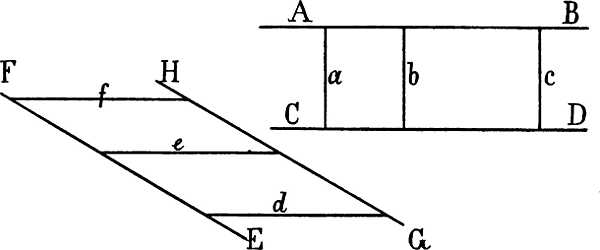
§ 2. Linien, welche nicht parallel sind, stehen in einem Winkel zu einander. Treffen sie in einem Punkte zusammen, wie in Fig. 2 b c und c d in c oder a b und b c in b, so heisst dieser Punkt die Spize des Winkels; die beiden den Winkel bildenden Linien heissen seine Schenkel. Wenn man von der Grösse eines Winkels spricht, so ist damit der Grad gemeint,[2] in welchem beide Schenkel desselben gegen einander geneigt sind; der Winkel bei c ist z. B. kleiner, als der Winkel bei b; die Länge der Schenkel kommt hiebei nicht in Betracht.

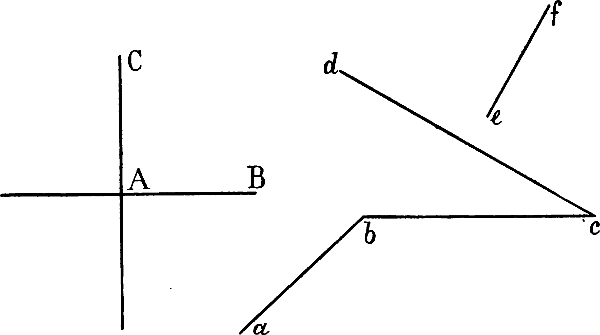
Eine senkrechte und eine wagrechte Linie, oder 2 schräge Linien, welche in demselben Grade gegen einander geneigt sind, wie eine senkrechte und eine wagrechte, bilden einen rechten Winkel, vgl. Fig. 2 A B und A C, e f und c d. Werden die Schenkel eines rechten Winkels über die Spize hinaus verlängert, so entstehen 4 rechte Winkel (z. B. bei A). Zwei Linien, welche[3] weniger gegen einander geneigt sind, als die Schenkel eines rechten Winkels, bilden einen stumpfen solche, die stärker gegen einander geneigt sind, einen spizen Winkel. Ein stumpfer Winkel (a b und c b, Fig. 2) ist also grösser, ein spizer Winkel (b c und c d) ist kleiner, als ein rechter.

Dreiecke.

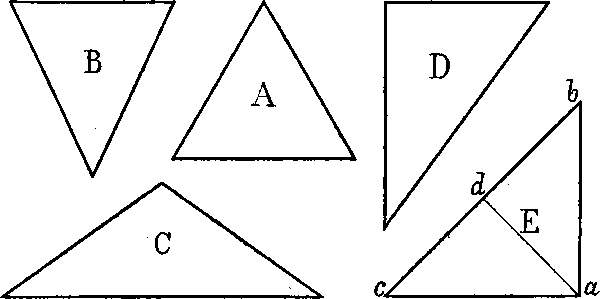
§ 3. A, B, C, D, E Fig. 3 sind verschiedene Arten von Dreiecken: A, ein gleichseitiges Dreieck, hat 3 gleich lange Seiten, welche in den Ecken 3 gleich grosse spize Winkel bilden; B, C und E sind gleichschenklige Dreiecke, in welchen 2 Seiten gleich lang sind, während die dritte entweder länger oder kürzer ist, als jene beiden; leztere heisst die Grundlinie. D und E sind rechtwinklige Dreiecke, d. h. einer der 3 Winkel ist ein rechter; E ist also ein gleichschenkliges rechtwinkliges Dreieck: der Winkel bei a ist ein rechter, a b und a c sind gleich lang; die Winkel bei b und c sind halbe[4] rechte Winkel; durch eine Linie von a nach d, der Mitte von b c, entstehen 2 rechtwinklige gleichschenklige Dreiecke: a d c und a d b.

Vierecke.

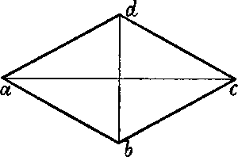
§ 4. Fig. 4 ist ein Quadrat, d. h. ein Viereck mit 4 gleich langen Seiten, welche in den Ecken 4 rechte Winkel bilden; in einem Rechteck oder Oblongum (Fig. 5) stossen die Seiten gleichfalls in rechten Winkeln zusammen, aber das eine Seitenpaar ist länger, als das andere. Fig. 6 ist eine Raute oder ein Rhombus: die 4 Seiten sind gleich lang und die gegenüberliegenden sind parallel, wie im Quadrat, aber sie bilden in den Ecken nicht rechte, sondern 2 spize und 2 stumpfe Winkel.

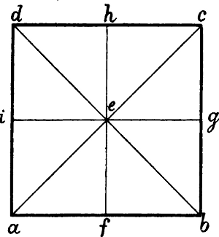
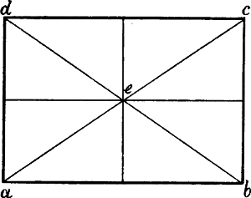
Vierecke, in welchen die gegenüberliegenden Seiten parallel sind, also Quadrat, Rechteck und Raute, heissen Parallelogramme. Die Linien a c und b d in Fig. 4, 5 und 6, welche die gegenüberliegenden Ecken eines Parallelogrammes verbinden, heissen Diagonalen. Die beiden Diagonalen eines Parallelogramms sind gleich lang, und schneiden sich im Mittelpunkt desselben. Zieht man durch den Punkt e, in welchem sie sich[5] schneiden, Linien, welche mit den Seiten parallel sind, so werden leztere halbiert. Im Quadrat werden die rechten Winkel der Ecken durch die Diagonalen halbiert. Diese stehen zu einander in einem rechten, zu den Seiten des Quadrats in einem halben rechten Winkel. e a b, e b c, e c d und e d a Fig. 4 sind 4 rechtwinklige, gleichschenklige Dreiecke, welche durch die Linien e f, e g, e h und e i wieder in je 2 solche Dreiecke geteilt werden.

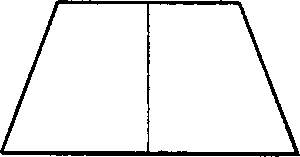
Ein Viereck, in welchem 2 Seiten parallel, die beiden andern nicht parallel sind, heisst Trapez (Fig. 7.)

Der Kreis; Hilfsmittel zum perspectivischen Zeichnen.

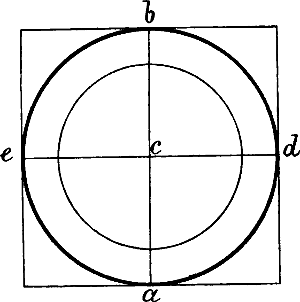
§ 5. Der Kreis (Fig. 8) ist eine gebogene Linie, welche überall gleich weit von einem Punkte, ihrem Mittelpunkt, entfernt ist. Durchmesser des Kreises heisst eine gerade Linie, welche von einem beliebigen Punkte der Kreislinie durch den Mittelpunkt hindurch nach dem entgegengesezten Punkt derselben gezogen wird, wie a b; eine gerade Linie vom Mittelpunkt nach einem beliebigen Punkt der Kreislinie, z. B. c a, c b, c d, c e, welche somit die Hälfte eines Durchmessers bildet, heisst Halbmesser oder Radius. Alle Radien eines Kreises[6] sind gleich lang. Concentrische Kreise sind Kreise, welche denselben Mittelpunkt haben.

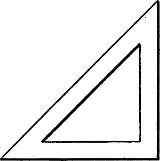
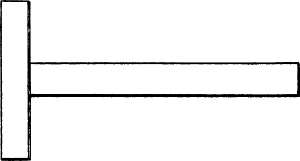
Als Hilfsmittel sind zum perspectivischen Zeichnen erforderlich: ein grösseres Reissbrett, ein Zirkel, ein rechter Winkel (Fig. 9) und eine Reissschiene (Fig. 10); durch leztere erhält man, indem der kurze Teil an den Rand des Reissbretts angelegt wird, auf bequeme Weise die senkrechten und wagrechten Linien.

II. Grundbegriffe der Perspective.

Unterschied der geometrischen und perspectivischen Form.

§ 6. Einen Gegenstand perspectivisch zeichnen heisst ihn so zeichnen, wie er dem Auge erscheint, wenn wir ihn von einem bestimmten Standpunkte aus betrachten. Dieses scheinbare oder perspectivische Bild der Dinge ist vielfach verschieden von der Form, welche sie in Wirklichkeit haben, d. h. ihrer geometrischen Form; während leztere unverändert bleibt, ändert sich die perspectivische Form eines Gegenstands mit jeder Veränderung unseres Standpunkts oder mit jeder Veränderung in der Stellung des betreffenden Gegenstandes.

Die geometrische Form eines Würfels (cubus) ist z. B. die eines Körpers, welcher von 6 gleich grossen quadratischen, rechtwinklig aneinanderstossenden Flächen begrenzt wird. Die Umrisslinien dieser Flächen sind geometrisch gleich lang, ihre geometrische Richtung ist, wenn wir den Würfel auf eine wagrechte Fläche stellen, teils senkrecht, teils wagrecht, sie stehen geometrisch teils parallel, teils rechtwinklig zu einander. Stellen wir aber mehrere in Wirklichkeit gleich grosse Würfel in verschiedener Stellung und Entfernung vor uns, oder betrachten wir denselben Würfel von verschiedenen Standpunkten aus, so erhalten wir sehr verschiedene Bilder, wie Fig. 11 zeigt: während einige Linien, wie a b, b c, c d in A, ihre geometrische Richtung und Länge behalten, erscheint ein Teil der geometrisch wagrechten Linien schräg, wie c e in A, a b, a g, c d, c e, d f[8] und e f in B, zuweilen auch senkrecht, wie d f in A; geometrisch parallele Linien erscheinen nicht mehr parallel, wie c e und d f in A, von den geometrisch gleich grossen Linien und Flächen erscheint bald die eine, bald die andere grösser oder kleiner u. s. w. Und während in Wirklichkeit die Gegenstände und ihre einzelnen Teile und Linien nicht nur neben und über einander, sondern auch in den verschiedensten Entfernungen vor und hinter einander liegen, sehen wir sie perspectivisch so, als ob sie in einer senkrechten Fläche sämtlich neben und über einander lägen, weshalb wir denn auch auf der Fläche des Papiers, der Leinwand u. s. w. das naturgetreue Bild eines Gegenstandes wiedergeben können. Die deutlichste[9] Anschauung hievon gibt das fotografische Abbild oder das Spiegelbild. Wenn wir einen Gegenstand, ohne unser Auge von der Stelle zu bewegen, so wie wir ihn in einem Spiegel oder durch eine Fensterscheibe sehen, auf der Fläche des Glases nachzeichnen, so erhalten wir sein genaues perspectivisches Bild.

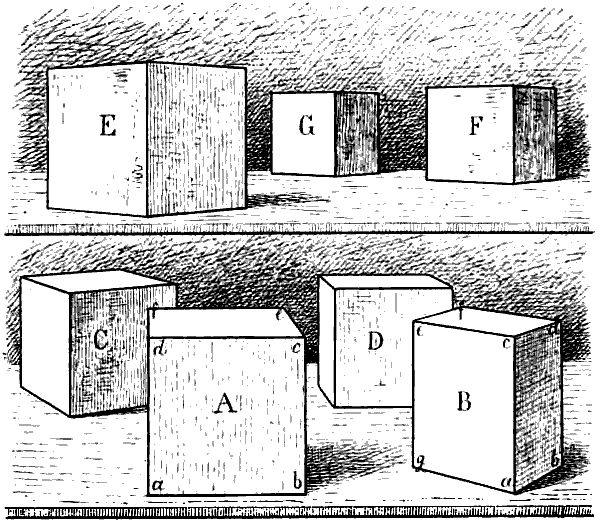
§ 7. Es ist die Erfahrung und Übung des Auges, welche bewirkt, dass wir die perspectivische Form, in der wir die Dinge sehen, nicht mit ihrer wirklichen oder geometrischen Form verwechseln, sondern uns auch da, wo die erstere von der lezteren abweicht, eine allerdings nicht immer genaue Vorstellung von der wirklichen Form des betreffenden Gegenstands machen können; dass wir z. B. bei Betrachtung von mehreren, wie A, B, C, D, E, F, G Fig. 11 sich darstellenden Würfeln uns ihrer verschiedenen Entfernung von unserem Standpunkt, der geometrisch wagrechten und parallelen Richtung der Linien c e, d f u. s. w. in A, der geometrisch gleichen Länge sämtlicher Umrisslinien der Würfel bewusst sind.

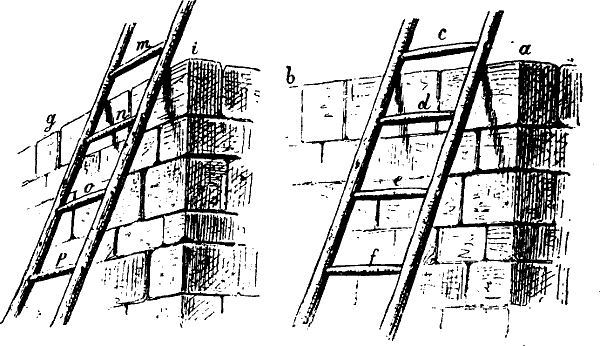
Ja, diese auf der Erfahrung unseres Auges beruhende Kenntnis der geometrischen Form bildet ein nicht unwesentliches Hindernis für die richtige Auffassung des perspectivischen Bildes.2 Unbewusst halten wir in dem häufigen und mannigfachen Wechsel der perspectivischen Erscheinung die Vorstellung der geometrischen Form fest und der ungeübte Zeichner ist deshalb stets geneigt, auch wo das seinem Auge sich darbietende Bild eines Gegenstands von dessen wirklicher Form erheblich abweicht, die leztere an Stelle des ersteren zu sezen, oder wenigstens mehr als richtig ist, der geometrischen Form nahe zu bleiben. Er wird z. B. Flächen oder Linien, welche von dem angenommenen Standpunkt aus im Verhältnis zu andern kleiner erscheinen, als sie in Wirklichkeit sind, fast immer zu gross, in Fig. 12 z. B. a b statt i g (das linke Bild als das[10] richtige angenommen), geometrisch rechtwinklige Linien, welche perspectivisch einen stumpfen oder spizen Winkel bilden, meist so zeichnen, dass sie wenigstens annähernd rechtwinklig zu einander stehen, vgl. c, d, e, f statt m, n, o, p; erscheint eine geometrisch wagrechte Linie perspectivisch schräg, so wird er sie zu wenig von der wagrechten Richtung abweichen lassen, vgl. a b u. s. w.

§ 8. Jede Berechnung einer perspectivischen Form muss zunächst ausgehen von der geometrischen Form des betreffenden Gegenstands: um zu berechnen, welche Richtung und welche Länge eine bestimmte Linie unseres Bildes haben soll, müssen wir die wirkliche Richtung und Länge der betreffenden Linie kennen und nur soweit, als wir diese genau anzugeben vermögen, ist ein genaues Resultat unserer Berechnung möglich.

Aber, wie bereits angedeutet, ist unsere Beurteilung der geometrischen Form nicht eine unbedingt sichere und genaue, wenn wir (siehe Vorwort) voraussezen, dass wir ohne Hilfe von Messungen am Gegenstand die wirkliche Form desselben[11] nur auf Grund unserer Anschauung und Erfahrung uns klar zu machen haben.

Auch ein geübtes Auge vermag die geometrische Form der Dinge nur dann mit vollkommener Bestimmtheit und Genauigkeit zu erkennen, wenn dieselbe eine regelmässige, durch die Natur des Gegenstands notwendig bedingte und dem Auge aus Erfahrung bekannte, nicht aber, wenn sie unregelmässig, zufällig und willkürlich ist. Unsere Berechnung wird sich daher nur auf Formen der ersteren Art erstrecken.

Teils aus diesem Grunde, teils weil wir bei Ausführung einer perspectivischen Berechnung auf das Lineal angewiesen sind, haben wir es zunächst nur mit geraden Linien zu thun. Doch ist damit die Anwendung der perspectivischen Regeln auf Formen, welche nicht geradlinige Umrisse haben, nicht ausgeschlossen, indem wir mittels gerader Linien die Lage einzelner wichtiger Punkte ihres perspectivischen Bildes berechnen können, von welchen aus das Übrige sich leicht aus freier Hand ergänzen lässt, wie dies z. B. bei der Darstellung eines von der Seite gesehenen Kreises geschieht, vgl. Fig. 93 und 94.

§ 9. Welche Linienrichtungen und Grössenverhältnisse sind nun als regelmässig und notwendig, welche als willkürlich anzusehen?

Bei aufmerksamer Betrachtung von Gegenständen der verschiedensten Art werden wir finden, dass es meist durch die Natur des betreffenden Gegenstandes bedingt und, auch wenn das perspectivische Bild von der geometrischen Form abweicht, deutlich wahrnehmbar ist, ob eine Linie geometrisch senkrecht, wagrecht, oder schräg ist, welche Linien geometrisch parallel, welche rechtwinklig zu einander stehen. Dasselbe gilt von den symmetrischen Grössenverhältnissen. (Da die Entfernung zweier Punkte von einander nach der Länge einer zwischen ihnen gezogenen geraden Linie bemessen wird, so bezieht sich das Gesagte auch auf die perspectivischen Entfernungen).

Wo dagegen Linien in einem spizen oder stumpfen Winkel zu einander stehen, ist die geometrische Größe dieses Winkels meist zufällig und willkürlich. (Eine Ausnahme bilden die Winkel, in welchen die Linien mancher geometrischen Figuren zu einander stehen, z. B. die Diagonalen eines Quadrats zu dessen Seiten, die Seiten eines gleichseitigen Dreiecks, eines Sechsecks, Achtecks u. s. w. zu einander). Alle Grössenverhältnisse, mit Ausnahme der symmetrischen, sind mehr oder weniger willkürlich.

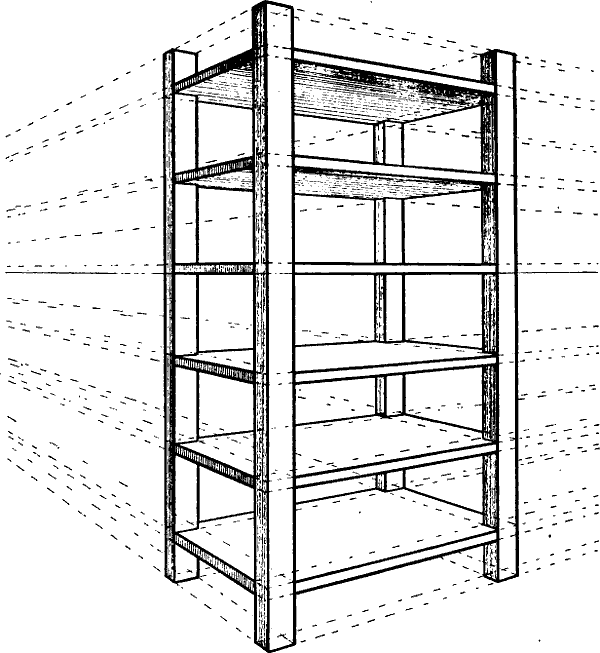
§ 10. Nehmen wir z. B. an, dass das Haus Fig. 13 und das Zimmer Fig. 14 so, wie sie hier gezeichnet sind, in Wirklichkeit vor uns stehen und dass die geometrische Richtung und Länge der verschiedenen Linien angegeben werden soll.

Leicht erkennbar sind überall die senkrechten Linien, da ihre Richtung stets unverändert dieselbe ist. Beispiele geometrisch wagrechter Linien sind in beiden Figuren die mit a, b, c, d, e, f, g, h bezeichneten Linien, geometrisch schräg sind in Fig. 13 i, h, k, m, n, o. Geometrisch parallel sind in Fig. 13 die Wagrechten a a und b, sodann die mit c und die mit e, ferner die mit f bezeichneten Linien und die schrägen Linien i i, sowie o o. In Fig. 14 sind geometrisch parallel die mit e, sodann die mit f bezeichneten Linien; ebenso a und b, c und d, g und h. Geometrisch rechtwinklig stehen zu einander in beiden Figuren die Linien a und b zu c und d, ferner die Linien e zu f.

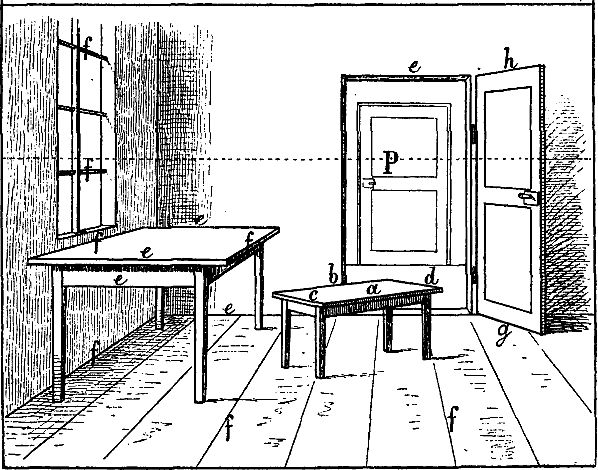
In Fig. 13 haben die 5 Fenster des ersten Stockwerks in Wirklichkeit gleiche Höhe, und Breite, die Entfernungen der Fenster von einander und von den Ecken sind je auf einer Seite geometrisch gleich gross, die Giebellinien i und k sind geometrisch gleich lang, ebenso in Fig. 14 die 4 Tischbeine, die 2 senkrechten Linien der Thüre (zwischen g und h) u. s. w.

Die rasche und sichere Auffassung solcher geometrischen Linienrichtungen und Grössenverhältnisse erfordert immerhin einige Übung. Dass die geometrisch schräge Linie m Fig. 13 (oder die geometrisch wagrechte a b Fig. 29) mit einer Senkrechten[14] verwechselt werde, ist kaum zu befürchten; leichter geschieht es, dass der Anfänger die geometrisch parallele oder rechtwinklige Stellung von Linien übersieht, welche nicht in Einer Fläche liegen oder wegen ihrer geringen Länge wenig in's Auge fallen (z. B. dass die Linie b, Fig. 13 geometrisch parallel ist mit a a). Bei einiger Aufmerksamkeit gewöhnt sich jedoch das Auge bald an eine richtige Unterscheidung der angeführten Linienrichtungen und Grössenverhältnisse.

Aber weder unser Auge noch unsere Erfahrung sagen uns genau, wie gross in Wirklichkeit der Winkel ist, in welchem die Linien i und k Fig. 13 zu der darunter liegenden Wagrechten c, oder in Fig. 14 die Linien a und b, c und d oder g und h zu e e stehen, wie breit in Wirklichkeit die linke Seite des Hauses Fig. 13 im Verhältnis zur rechten, das Fenster Fig. 14 im Verhältnis zur vorderen, dieser zum anstossenden Tischrand ist; denn alle diese Winkelstellungen und Grössenverhältnisse ergeben sich nicht aus der Natur des Gegenstandes; sie sind zufälliger Art.

§ 11. Da die zufälligen und willkürlichen Linienrichtungen, Winkelstellungen und Grössenverhältnisse, deren Darstellung wir dem Auge und der Übung des Zeichners überlassen, überall häufig vorkommen, in der landschaftlichen Natur sogar weit vorherrschen über das Regelmässige und Notwendige der Form, so könnte es scheinen, als ob die Anwendung und der Nuzen perspectivischer Geseze und Studien sehr beschränkt sei. Aber es ist klar, dass die Genauigkeit der Zeichnung eine um so grössere sein muss, die Kenntnis und Anwendung bestimmter Regeln daher um so notwendiger ist, je bekannter und regelmässiger die darzustellenden Formen sind, während unregelmässige und willkürliche Formen der Darstellung eine grössere Freiheit gestatten. Hievon abgesehen beruht der Wert perspectivischer Studien nicht allein darin, dass sie uns in Stand sezen, das perspectivische Bild eines Gegenstands mathematisch zu berechnen, sondern wir lernen durch dieselben überhaupt[15] die Eindrücke des Auges mit richtigerem und klarerem Verständnis aufzufassen und infolge dessen auch da, wo keine genauere Berechnung stattfindet, richtiger wiederzugeben.

Der Standpunkt; Sehkreis, Augpunkt, Horizont.

§ 12. Nächst der geometrischen Richtung und Länge der Linien ist es ihre Stellung zu unserem Auge, oder, was dasselbe ist, unseres Auges zu ihnen, d. h. unser Standpunkt, wovon das perspectivische Bild abhängt. Gewöhnlich versteht man unter Standpunkt die Stelle, auf welcher wir stehen oder sizen; im Sinne der genauen perspectivischen Berechnung jedoch verstehen wir darunter den Punkt, wo unser Auge sich befindet. Der Unterschied zwischen rechtem und linkem Auge kommt dabei nicht in Betracht wegen der als notwendig vorausgesetzten Entfernung unseres Standpunkts von dem zu zeichnenden Gegenstand.

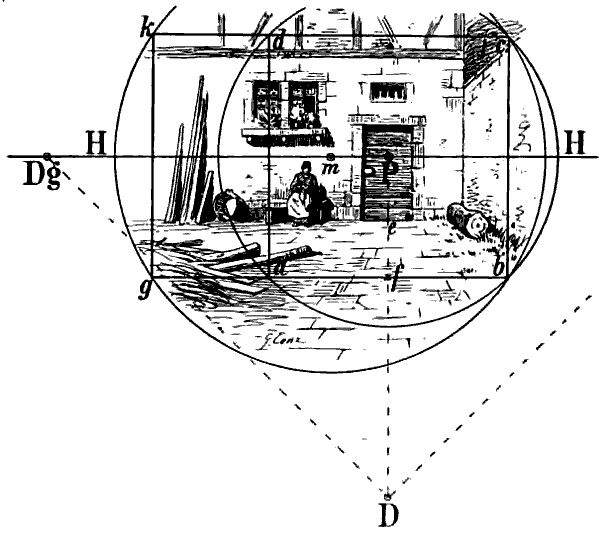
Da wir nach allen Richtungen gleich viel übersehen, so bildet der Umfang dessen, was wir mit Einem Blick erfassen können, einen – selbstverständlich nicht bestimmt abgegrenzten – Kreis, unsern Sehkreis, vgl. Fig. 15. Der Mittelpunkt desselben, P, ist der Punkt, welcher dem Auge gerade gegenüber liegt und heisst der Augpunkt. Durch den Augpunkt denke man sich eine wagrechte den Sehkreis in der Mitte durchschneidende und nach beiden Seiten über denselben hinaus beliebig sich fortsezende Linie (H H) gezogen; dies ist der perspectivische Horizont. Die perspectivische Berechnung geht von der Voraussezung aus, dass der Blick des Zeichners bei aufrechter Haltung des Kopfes geradeaus gerichtet sei, so dass beide Augen in einer wagrechten Linie liegen, welche wir unsere Augenlinie nennen. Mit dieser Linie parallel-laufend und in gleicher Höhe mit ihr haben wir uns den Horizont zu denken. Eine von unserem Auge nach dem Augpunkt gezogene Linie würde demnach rechtwinklig zu unserer[17] Augenlinie und zum Horizont stehen wie D P zu H H in Fig. 15. Man denke sich die Zeichnung senkrecht stehend und D P als wagrechte rechtwinklig zu H H stehende Linie, vgl. Fig. 16.

Im gewöhnlichen Sprachgebrauch bedeutet Horizont die Linie, welche die sichtbaren Gegenstände gegen den Himmel abgrenzt, es sei dies eine Berglinie, oder der obere Umriss von Gebäuden u. s. w. Dieser sogenannte scheinbare Horizont ist zugleich unser perspectivischer, wenn wir eine wagrechte, soweit das Auge reicht vor uns ausgedehnte Fläche überblicken. Eine solche Fläche erscheint gegen den Himmel begrenzt durch eine wagrechte in gleicher Höhe mit unserem Auge liegende Linie, wie uns am deutlichsten die Meeresfläche zeigt: je tiefer wir stehen, desto schmaler, je höher wir stehen, desto breiter erscheint uns dieselbe, mit unserem Standpunkt scheint auch die Grenzlinie des Meeres höher oder tiefer zu rücken,3 vgl. Fig. 17 und 18.

§ 13. Indem wir Augpunkt und Horizont auf unserer Zeichnung angeben (was in sämtlichen Figuren durch die Buchstaben P und H H geschehen ist), bezeichnen wir damit die Höhe und die Richtung, aus welcher wir den betreffenden Gegenstand sehen und zeichnen. In Fig. 15 haben wir uns demnach den Zeichner in der Fortsezung der Linie e f stehend oder sizend zu denken, so dass sein Auge dem Punkte P gerade gegenüber und in gleicher Höhe mit diesem und mit der Linie H H sich befände, vgl. Fig. 16.

Um beim Zeichnen nach der Natur Augpunkt und Horizont an der richtigen Stelle anzugeben, muss man zuvor, so gut dies ohne Berechnung möglich, eine Skizze der Hauptlinien des[19] Bildes nach ihren ungefähren Verhältnissen entworfen haben. Hält man hierauf einen Bleistift, den Rand des Zeichenblattes oder dgl. wagrecht in gleicher Höhe mit dem Auge vor sich, so ist es nicht schwer, die Höhe zu ersehen, in welcher der Gegenstand von der Horizontlinie durchschnitten wird und auf derselben die dem Auge gerade gegenüberliegende Stelle zu bestimmen.

Gewöhnlich wird übrigens nicht der ganze Umfang des Sehkreises als Bild verwendet. Wir pflegen vielmehr der Zeichnung die Form eines Rechtecks zu geben, welches in der Regel so abgegrenzt wird, dass Horizont und Augpunkt nicht in der Mitte, aber auch nicht zu nahe am Rande desselben liegen, vgl. Fig. 17 und 18.

Die Distanz.

§ 14. Unter der Entfernung unseres Standpunkts oder der Distanz ist zu verstehen unsere Entfernung von den uns zunächst liegenden Teilen des zu zeichnenden Gegenstands. Häufig liegt der nächste Vordergrund in der wagrechten Fortsezung der Fläche, auf welcher wir unsern Standpunkt genommen haben und bildet so den untern Rand der Zeichnung, wie in Fig. 13–15. Ziehen wir in solchem Fall eine Linie von unserem Fuss nach dem gerade gegenüber liegenden Punkt der Vordergrundlinie, dem sog. Fusspunkt, so bezeichnet die Länge dieser Linie (F f Fig. 16) die genaue Grösse unserer Distanz.

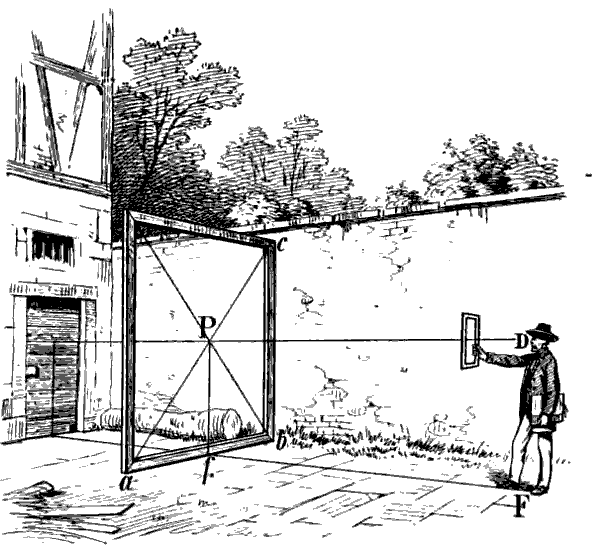
Denken wir uns, dass anstossend an den Teil unseres Gegenstands, welcher unserem Auge am nächsten liegt, z. B. in Fig. 15 und 16 auf der Linie a b, eine grosse unser ganzes Bild umfassende Glastafel stehe und dass Augpunkt, Horizont und Fusspunkt in der senkrechten Fläche dieser Tafel (der sogenannten Bildfläche) liegen, so wäre eine Linie vom Auge nach dem Augpunkt eben so lang, als eine Linie von unserem Fusse nach dem Fusspunkt (vgl. D P und F f Fig. 16) und[20] könnte ebenso als Mass der Distanz gebraucht werden. In diesem Sinne ist es zu verstehen, wenn gesagt wird, die Distanz bedeute die Entfernung unseres Auges vom Augpunkt, und so oft von dieser die Rede ist, muss man sich das zu zeichnende Bild in der angeführten Weise als eine senkrechte Fläche vorstellen, wie wir es im Spiegelbilde sehen.

§ 15. Die Entfernung des Standpunkts muss wenigstens so gross sein, dass der Zeichner gerade aus in der Richtung des Augpunkts blickend und ohne das Auge nach der Seite, nach oben oder unten zu wenden, alles, was er in sein Bild aufnehmen will, deutlich übersehen kann.

Denn da bei jeder Veränderung des Standpunkts das perspectivische Bild des Gegenstands ein anderes wird, so ist die erste Bedingung einer perspectivisch richtigen Zeichnung, dass das Ganze von ein und demselben Standpunkt aus, d. h. aus derselben Höhe, Richtung und Entfernung gezeichnet, die einmal angenommene Lage von Horizont und Augpunkt, sowie die Grösse der Distanz unverändert beibehalten werde. Sobald wir aber die Richtung unseres Blickes verändern, so ändert sich die Lage unseres Augpunkts und somit unser Standpunkt.

Die Grösse der Distanz muss demgemäss in einem gewissen Verhältnis zum Umfang des zu zeichnenden Gegenstandes stehen: je grösser derselbe sein soll, desto grösser muss auch die Distanz sein.

§ 16. Man nimmt an, dass das Auge eine ihm senkrecht gegenüberstehende kreisrunde oder quadratische Fläche vollständig in der angeführten Weise übersehen kann, wenn seine Entfernung vom Mittelpunkt dieser Fläche wenigstens so gross ist, als ein Durchmesser oder eine Diagonale derselben. Dabei ist vorausgesezt, dass sich das Auge dem Mittelpunkt der Fläche gegenüber befinde.

Wenn wir uns z. B. das Quadrat a b c d Fig. 15 als eine senkrecht vor uns stehende Glastafel denken, deren Mittelpunkt[21] unser Augpunkt und deren Diagonale (a c oder b d) 4½ Meter lang wäre, so müsste unser Auge von dem Mittelpunkt dieser Tafel wenigstens 4½ Meter entfernt sein, um ohne Veränderung des Standpunkts den ganzen Umfang derselben übersehen zu können. Oder wenn in Fig. 16 P Augpunkt des in F stehenden Beschauers und a b c d eine quadratische Glastafel ist, so müssen die Linien D P und F f wenigstens so lang sein wie a c und b d, damit das Auge von D aus die ganze Tafel und alles, was durch dieselbe sichtbar ist, übersehen kann.

Befindet sich das Auge nicht dem Mittelpunkt der Bildfläche gegenüber, so ist die Diagonale derselben noch kein hinreichendes Mass der Distanz. Wenn wir z. B. dem Bilde a b c d Fig. 15 so gegenüberstehen, dass m unser Augpunkt ist, so muss, um den von dem Viereck a b c d umschlossenen Raum übersehen zu können, die Distanz wenigstens doppelt so gross sein, als eine Linie von m nach b oder nach c, d. h. eben so gross als für ein Rechteck g b c k erforderlich wäre, dessen Mittelpunkt m ist oder für einen von m aus durch c und b beschriebenen Kreis.

§ 17. Natürlich ist das Gesagte nicht so aufzufassen, als ob innerhalb eines bestimmten Umkreises alle Gegenstände gleich deutlich, jenseits desselben undeutlich oder gar nicht mehr sichtbar wären, vielmehr nimmt die Deutlichkeit derselben allmälig ab, je weiter sie sich vom Augpunkt entfernen. Es ist aber für die perspectivische Berechnung notwendig, eine Grenzlinie festzusezen, innerhalb deren eine hinreichende Deutlichkeit des Bildes anzunehmen ist. Dieses Mass der kleinsten Distanz ist in den perspectivischen Lehrbüchern verschieden angegeben, wie auch der Umfang dessen, was mit Einem Blick zu übersehen ist, nicht für jedes Auge gleich gross ist. Jedoch kann ohne Gefahr für eine perspectivisch richtige Wirkung nicht wohl ein niedrigeres Mass angenommen werden, als oben geschehen ist.

Ist es dem Zeichner durch die Raumverhältnisse unmöglich gemacht, seinen Standpunkt in hinreichender Entfernung zu nehmen, so muss mittels perspectivischer Berechnung das Ganze so gezeichnet werden, wie es sich, in richtiger Entfernung gesehen, dem Auge darstellen würde.4

§ 18. Die Grösse der für eine Zeichnung angenommenen Distanz wird ausgedrückt durch die Distanzpunkte. Ein Distanzpunkt ist ein senkrecht über oder unter dem Augpunkt oder seitwärts von diesem in der Horizontlinie angegebener Punkt, dessen Entfernung vom Augpunkt (im Verhältnis der Zeichnung) der Entfernung unseres Auges vom Augpunkt oder unseres Fusses vom Fusspunkt entspricht. Ist z. B. in Fig. 15 die Linie a b 3 Meter lang und ist die vom Zeichner für das Bild a b c d angenommene Distanz eine solche, dass sein Fuss von f, sein Auge von dem (senkrecht über f gedachten) Augpunkt P 4½ Meter entfernt sich befindet, so sind D und Dg Distanzpunkte, indem eine Linie von einem dieser 2 Punkte bis P 1½ mal so gross ist, als a b.

Zur Unterscheidung werden wir die seitwärts vom Augpunkt liegenden Distanzpunkte Diagonalpunkte nennen (Dg und Dp). Von den beiden andern ist stets der unterhalb des Augpunkts liegende verwendet und als Distanzpunkt (D) bezeichnet.

Aus § 16 folgt, dass ein Distanzpunkt oder Diagonalpunkt nie innerhalb der Zeichnung liegen kann, da seine Entfernung vom Augpunkt wenigstens so gross sein muss, als eine Diagonale derselben, wenn der Augpunkt in der Mitte des Bildes liegt, oder, wenn dies nicht der Fall ist, doppelt so gross als eine Linie[23] vom Augpunkt nach dem von ihm entferntesten Punkte der Zeichnung.

§ 19. Ein genaues Abmessen der Distanz ist natürlich in den meisten Fällen nicht ausführbar und ist auch behufs Angabe der Distanzpunkte nicht notwendig. Die Hauptsache ist, dass eine zu kleine Distanz vermieden wird. Um sich beim Zeichnen nach der Natur zu versichern, dass die angenommene Entfernung des Standpunkts eine für den beabsichtigten Umfang des Bildes hinreichende sei, kann man sich eines aus starker Pappe gefertigten Rahmens bedienen, dessen innerer Rand ein Rechteck von 48 : 36 Centimeter bildet. Die Diagonale eines Rechtecks von dieser Grösse entspricht ungefähr der durchschnittlichen Länge des Arms; die Distanz ist also hinreichend gross, wenn der Rahmen, auf Armeslänge vor das Auge gehalten, während der Blick auf den Augpunkt gerichtet ist, den ganzen Gegenstand, welcher gezeichnet werden soll, umschliesst, vgl. Fig. 16. Hiebei wird man sich leicht überzeugen, dass der Umfang des innerhalb des Rahmens sichtbaren Bildes kleiner oder grösser wird, je nachdem man, denselben vor sich haltend, dem Gegenstande näher tritt oder sich von demselben entfernt.

§ 20. Wenn von der Entfernung einzelner Teile des Bildes von unserem Standpunkt die Rede ist, so kommt dabei nicht in Betracht, ob dieselben mehr in der Mitte oder nach dem Rande desselben liegen, da dies bei richtiger Grösse der Distanz keinen für die perspectivische Berechnung wesentlichen Unterschied macht, sondern es ist damit nur die Entfernung in der Richtung vom Vordergrund nach dem Hintergrund zu gemeint. Um die Entfernung eines Punktes oder einer Linie vom Auge in diesem Sinne zu bezeichnen, gebraucht man häufig den Ausdruck »Tiefe«. Man kann z. B. sagen: a und b Fig. 15 liegen in gleicher Tiefe, a und e in verschiedener Tiefe.

Das Grundgesez der perspectivischen Formerscheinung. Unverkürzte und verkürzte Stellung der Flächen und Linien.

§ 21. Das wichtigste und am meisten in die Augen fallende Gesez der Perspective ist, dass alle Gegenstände kleiner zu werden scheinen, je weiter sie sich von unserem Standpunkt entfernen. Alle perspectivischen Formveränderungen lassen sich auf dieses Gesez zurückführen, dessen Begründung wir im Bau unseres Auges und der hiedurch bedingten Art, wie sich in demselben die Gegenstände spiegeln, zu suchen haben.

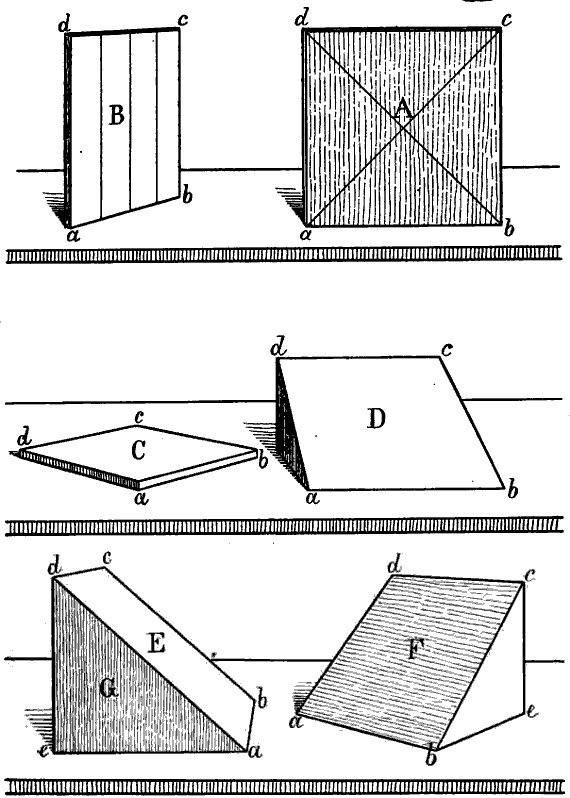
Aus jenem Gesez folgt zunächst, dass nur eine Fläche, welche ganz gerade vor uns steht, d. h. senkrecht und parallel mit unserer Augenlinie, wie die Fläche A Fig. 19, dem Auge genau so erscheinen kann, wie sie in Wirklichkeit ist, mit andern Worten so, dass die perspectivische Richtung und das perspectivische Grössenverhältnis ihrer Umrisse und aller in ihr liegenden Linien mit deren geometrischer Richtung und Länge übereinstimmt. Denn in diesem Fall befinden sich sämtliche Teile der Fläche in gleicher Entfernung vom Auge (in gleicher Tiefe). Sobald wir die Tafel A, während unser Standpunkt derselbe bleibt, nach irgend einer Seite wenden, so liegen einzelne Teile derselben in ungleicher Tiefe; die ferneren Teile erscheinen infolge dessen verhältnismässig kleiner, als die näheren und die perspectivische Form der ganzen Tafel wird hiedurch eine von ihrer geometrischen Form verschiedene. In B ist z. B. die Linie b c ferner als a d, jene erscheint daher kürzer als diese, folglich können die geometrisch parallelen Linien a b und d c nicht mehr parallel und sie können nicht mehr beide rechtwinklig zu a d und b c erscheinen. Wird die Tafel B in mehrere gleich grosse senkrechte Streifen geteilt, so erscheinen diese nach der Linie b c hin allmälig kleiner[26] zu werden, die ganze Fläche erscheint daher schmaler als bei der Stellung A, vgl. Fig. 11.

§ 22. Wenn eine Fläche oder Linie eine solche Stellung zum Auge hat (unser Standpunkt zu ihr ein solcher ist), dass sämtliche Teile derselben in gleicher Tiefe liegen, wie in Fig. 19 A und die an A befindlichen Linien, so nennt man dies die unverkürzte Stellung; eine Fläche oder Linie ist dagegen verkürzt, wenn einzelne Teile derselben dem Auge näher, andere ferner liegen. Unverkürzt sind also in Fig. 19 die Flächen A und G, sämtliche senkrechte Linien, die wagrechten Linien a b und c d in A und D, a e in G, die schrägen Linien a c und b d in A, a d und b c in E. Alle übrigen Flächen und Linien sind verkürzt. (Man bemerke, dass zwar die schräge Fläche E verkürzt ist, da b c ferner liegt als a d, die schrägen Linien a d und b c aber in E unverkürzt sind, indem ihre beiden Endpunkte in gleicher Tiefe liegen).

Die senkrechten Linien haben immer unverkürzte Stellung, da ihre beiden Endpunkte immer in gleicher Tiefe liegen. Eine senkrechte Fläche dagegen kann sowohl verkürzt sein wie B, als unverkürzt wie A.

Die unverkürzten wagrechten Linien eines Bildes sind parallel mit unserer Augenlinie und mit dem Horizont, folglich auch parallel unter sich. Wagrechte und schräge Flächen sind stets verkürzt.

§ 23. Für Anfänger ist es zweckmässig, einen Bleistift, ein Lineal oder dergl. in der für die Zeichnung angenommenen Richtung der Augenlinie und des Horizonts vor sich zu legen, um mit dieser Normallinie die verschiedenen wagrechten Linien des Gegenstands vergleichen und leichter unterscheiden zu können, ob sie unverkürzt oder verkürzt sind.

Sollte man in Betreff einer schrägen Linie im Zweifel sein, ob sie unverkürzt oder verkürzt ist, so denke man sich dieselbe mit einer senkrechten und einer wagrechten Linie zu einem Dreieck verbunden, wie in G die schräge Linie a d mit[27] a e und e d oder in F die Linie b c mit b e und e c. Man nennt dies das Massdreieck einer schrägen Linie. Ist die wagrechte Linie dieses Dreiecks unverkürzt, wie a e in G, so ist es auch die schräge; ist erstere verkürzt, wie b e in F, so ist auch die schräge Linie verkürzt.

§ 24. Unverkürzte Linien, welche in gleicher Tiefe (in Einer unverkürzten senkrechten Fläche) liegen, wie sämtliche Linien der Fläche A Fig. 19, behalten ihre geometrische Richtung und ihr geometrisches Grössenverhältnis; sie erscheinen und werden gezeichnet wie sie in Wirklichkeit sind; unverkürzte Linien in ungleicher Tiefe, wie a d und b c in B, b c und a d in E, behalten ihre geometrische Richtung, nicht aber ihr geometrisches Grössenverhältnis (indem die ferneren kleiner erscheinen); die perspectivische Länge der verkürzten Linien ist immer, ihre perspectivische Richtung in den meisten Fällen verschieden von ihrer geometrischen Richtung und Länge.

Wo die geometrische Richtung oder Länge einer Linie unverändert bleibt, muss dieselbe entweder nach dem Augenmass oder mit Hilfe von Lineal und Zirkel bestimmt werden. Wir bedürfen für solche Fälle keiner perspectivischen Regel und Berechnung.

III. Perspectivische Richtung verkürzter Linien.

Verkürzte Parallellinien.

§ 25. Wenn 2 parallele Linien durch eine Anzahl von Linien verbunden werden, welche unter sich gleichfalls parallel sind, so sind nach § 1, Fig. 1 diese Verbindungslinien gleich lang. Haben wir nun parallele Linien in verkürzter Stellung vor uns, wie die Eisenbahnschienen in Fig. 20, so befinden sich die Verbindungslinien, hier die Schwellen, in verschiedener Entfernung vom Auge, sie scheinen daher nach der Ferne hin immer kleiner zu werden, d. h. der Abstand zwischen den beiden verkürzten Parallellinien scheint sich zu verkleinern, sie scheinen näher zusammenzurücken je weiter sie sich von unserem Auge entfernen und wenn sie sich auf sehr weite Entfernung fortsezen, so müssen sie schliesslich in Einem Punkte, wie hier in dem Punkte P, zusammentreffen, in welchem sie aufhören sichtbar zu sein.

Man nennt diesen Punkt den Fluchtpunkt oder Verschwindungspunkt der betreffenden Linien.

§ 26. In demselben Punkte, in welchem 2 verkürzte Parallellinien zusammentreffen, müssen auch alle weiteren mit ihnen parallelen Linien, wie in Fig. 20 die Linien a P, b P, c P, sich treffen, da der Zwischenraum zwischen allen in demselben Verhältnis nach der Ferne hin kleiner wird. Wenn a b, b c und c d gleich lang, a e und d f je halb so lang sind als a b, so müssen g h, h i und i k, m g und k n in demselben Verhältnis[29] zu einander stehen, sie werden also zugleich aufhören, sichtbar zu sein.

Wenn wir solche Linien auch nicht mit dem Auge verfolgen können bis zu dem Punkte, in welchem sie zusammentreffen würden, sondern sie nur in kürzerer Ausdehnung vor uns haben, wie die geometrisch parallelen Linien a a und b b in Fig. 21, so müssen sie stets so gezeichnet sein, dass der Zwischenraum zwischen ihnen nach der Ferne hin kleiner wird, so dass sie, von ihrem ferner liegenden Ende aus fortgesezt, irgendwo in Einem Punkte zusammentreffen würden, d. h.[30] verkürzte Parallellinien müssen die Richtung nach einem gemeinschaftlichen Fluchtpunkt haben.

Man vergleiche ausser Fig. 20 und 21 die wagrechten Parallellinien a a, c c, f f in Fig. 13 und 14, sämtliche wagrechte Linien in Fig. 22, die schrägen Parallellinien n n in Fig. 21, a c und e d, a g und e h in Fig. 36, a, b, c und d Fig. 37 und andere.

§ 27. Sobald wir also 2 verkürzte Parallellinien dieser Regel entsprechend gezeichnet haben, so ist damit auch die perspectivische Richtung aller weiteren mit ihnen parallelen[31] Linien gegeben: man verlängert die zuerst gezeichneten bis zu dem Punkte, in welchem sie zusammentreffen und zieht nach diesem die übrigen.

Wie zu verfahren ist, wenn ein Fluchtpunkt ausserhalb der Zeichnung liegt, wie die Fluchtpunkte der Linien a a, b b, n n in Fig. 21, wird später gezeigt werden. Häufig kann jedoch die genaue Berechnung in solchen Fällen dadurch ersezt werden, dass man einen Papierstreifen an das Zeichenblatt anlegt, um die betreffenden Linien bis zu ihrem Fluchtpunkt verlängern zu können, oder dass man wie in Fig. 21 und 22 sie wenigstens so weit als der Raum gestattet, fortsezt, da sich, je länger sie sind, desto deutlicher beurteilen lässt, ob sie die erforderliche Richtung nach Einem Punkte hin haben.

Verkürzte wagrechte Linien.

§ 28. Wenn wir am Ende eines Zimmers stehend Decke und Fussboden desselben betrachten, so scheint die erstere nach dem jenseitigen Ende des Zimmers hin zu fallen, der Boden scheint nach dorthin anzusteigen; ebenso scheinen alle wagrechten Flächen, welche höher liegen als unser Auge, nach der Ferne hin zu fallen, tiefer liegende scheinen zu steigen. Halten wir aber eine Fläche, z. B. ein dünnes Brett, ein Stück Pappe oder dergl. wagrecht in gleicher Höhe mit unserem Auge vor uns, so sehen wir weder die untere noch die obere Seite dieser Fläche, wir sehen sie nur als eine wagrechte Linie, welche, da der Horizont gleichfalls eine in der Höhe des Auges liegende wagrechte Linie ist, mit diesem zusammenfällt, vgl. Fig. 22. Alle wagrechten Flächen scheinen sich also nach dem Horizont hin zu neigen.

Denn alle wagrechten Flächen sind parallel und sind verkürzt. Daher scheint der Zwischenraum zwischen 2 wagrechten Flächen, z. B. zwischen Decke und Fussboden, nach der Ferne hin immer kleiner zu werden, sie scheinen einander näher zu[32] rücken, ebenso wie verkürzte parallele Linien. Wie diese nach Einem Punkte, so scheinen alle wagrechten Flächen nach Einer Linie hinzustreben und diese Linie kann nach dem Gesagten nur der Horizont sein: der Horizont ist die gemeinschaftliche Fluchtlinie oder Verschwindungslinie aller wagrechten Flächen.

§ 29. Mit den wagrechten Flächen scheinen auch die in ihnen liegenden verkürzten Linien 5 zu steigen oder zu fallen; jede wagrechte Linie kann als Teil einer wagrechten Fläche gedacht werden; folglich müssen verkürzte wagrechte Linien, wenn sie tiefer liegen als unser Auge, d. h. unterhalb des Horizonts, von ihrem näheren nach ihrem entfernteren Endpunkte zu steigen; wenn sie höher liegen als unser Auge, d. h. über dem Horizont, so müssen sie nach der Ferne hin fallen; wagrechte Linien aber, welche mit dem Auge in gleicher Höhe liegen, bleiben wagrecht, auch wenn sie verkürzt sind. Mit andern Worten: die Fluchtpunkte aller verkürzten wagrechten Linien liegen im Horizont; jede muss so gezeichnet sein, dass sie, von ihrem entfernteren Ende aus verlängert, in irgend einem Punkte den Horizont trifft und dieser Punkt ist zugleich der Fluchtpunkt aller mit ihr parallelen Linien; vgl. Fig. 20, 21, 22.

Haben wir also wagrechte Parallellinien in verkürzter Stellung zu zeichnen, so ist, sobald die perspectivische Richtung für eine derselben bestimmt ist, auch die Richtung der übrigen gegeben: man verlängert die erstere bis zum Horizont und nach dem Punkte, in welchem sie ihn trifft, werden die andern gezogen.

§ 30. Die Lage dieser Fluchtpunkte kann nun, wie schon die bisherigen Beispiele zeigen, eine sehr verschiedene sein. Es entsteht also die Frage, an welcher Stelle des Horizonts in diesem oder jenem Falle der Fluchtpunkt einer wagrechten Linie liegen muss, d. h. in welchem Grade die verschiedenen wagrechten Linien nach dem Horizont hin fallen oder steigen müssen.

Die allgemeine Regel in dieser Beziehung ist, dass der Fluchtpunkt einer verkürzten wagrechten Linie da liegt, wo eine parallel mit ihr vom Auge nach dem Horizont gezogene Linie diesen treffen würde. Denn verkürzte Parallellinien haben denselben Fluchtpunkt.

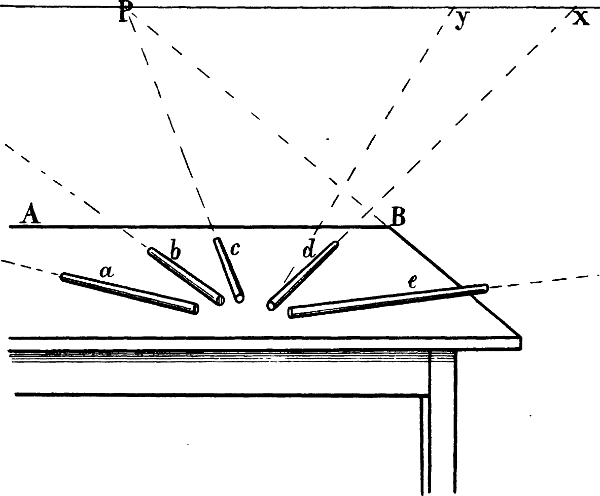
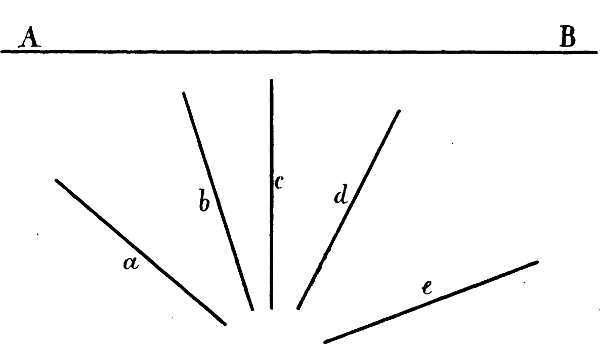
Z. B.: a, b, c, d, e Fig. 23 sind verkürzte wagrechte Linien, welche zu der unverkürzten Wagrechten A B verschiedene Winkel bilden. Der Horizont ist parallel mit den unverkürzten wagrechten Linien unseres Gegenstandes (§ 22), der Winkel also, in welchem eine verkürzte wagrechte Linie in Wirklichkeit zu einer unverkürzten Wagrechten steht, ist derselbe, in welchem sie auch zum Horizont steht. Die geometrische Stellung der Linien a, b, c, d, e zu A B Fig. 23 ist in Fig. 24 angegeben. Dies ist auch ihre Winkelstellung zum Horizont. Denken wir uns nun, dass die 5 Stäbe in Wirklichkeit so wie sie hier gezeichnet sind vor uns liegen und dass parallel mit denselben 5 Linien von unserem Auge nach dem Horizont gezogen seien, so müssten die Punkte, in welchen die von unserem Auge ausgehenden Linien den Horizont treffen, die Fluchtpunkte der 5 Stäbe sein. Wenn man sich hievon eine deutliche Vorstellung macht, etwa indem man einen langen Stab parallel mit einer verkürzten Linie des zu zeichnenden Gegenstands vor's Auge hält, so wird man die Lage ihres Fluchtpunkts annähernd bestimmen können; man wird z. B. verstehen, dass der Fluchtpunkt von e sehr weit nach rechts, der Fluchtpunkt von d näher nach dem Augpunkt hin liegen muss u. s. w.

§ 31. Die Stellung einer Linie zum Horizont ist jedoch immer eine willkürliche, da die Richtung des lezteren von der zufälligen Wahl unseres Standpunkts abhängt. Wenn wir die Lage des Fluchtpunkts einer wagrechten Linie genauer berechnen, so geschieht dies nicht, damit ihre Stellung zum Horizont, sondern damit ihre Stellung zu andern Linien des Bildes eine richtige Wirkung[36] mache. Nur wo es sich um eine bestimmte und notwendige Winkelstellung wagrechter Linien zu einander handelt, bedürfen wir einer genaueren Regel in Betreff der Lage ihrer Fluchtpunkte und können wir eine solche anwenden.

Nehmen wir z. B. in Fig. 23 als Fluchtpunkt der Linie d den Punkt y statt x an, so scheint der Winkel, in welchem d zu e steht, grösser, ihr Winkel zu c kleiner zu sein, als wenn x Fluchtpunkt ist. Aber die Winkelstellung dieser Linien zu einander und zu den übrigen Linien des Gegenstands ist ebenso willkürlich und zufällig, wie ihre Stellung zum Horizont. Mit blossem Auge würde der Beschauer auch nicht mit Bestimmtheit zu erkennen vermögen, dass ihre geometrische Stellung zu A B und zum Horizont oder ihre Stellung zu einander genau die in Fig. 24 angegebene ist. Also können wir auch die perspectivische Stellung dieser Linien zum Horizont und zu einander nicht genau berechnen und ist es für die perspectivische Richtigkeit der Zeichnung ohne Belang, ob beispielsweise y oder x als Fluchtpunkt der Linie d angenommen wird.

Ebenso ist in Fig. 14 die Winkelstellung der verkürzten wagrechten Linien g und h, sowie der Linien a, b, c, d zu den übrigen Linien des Bildes eine willkürliche. Notwendig ist nur, dass g und h, a und b, c und d als parallele Linien erscheinen und dass die Linien a, b, c, d ein Rechteck darstellen. Wir überlassen es deshalb dem Auge des Zeichners, zuerst die Richtung für eine der Linien g oder h und für eine Seite des genannten Rechtecks zu bestimmen, natürlich mit Rücksicht darauf, dass die Fluchtpunkte dieser Linien im Horizont liegen müssen, da sie geometrisch wagrecht sind. Aber angenommen, dass g und a die zuerst gezeichneten Linien seien, so ist damit nicht nur die perspectivische Richtung der mit jenen parallelen Linien h und b, sondern auch der rechtwinklig zu a stehenden Linien c und d gegeben. Für die Lage des Fluchtpunkts der 2 lezteren sind ebenso wie für die Richtung der verkürzten Parallellinien bestimmte Regeln massgebend.

Unsere nächste Aufgabe soll demgemäss die Beantwortung der Frage sein, welche Stellung in unserer Zeichnung wagrechte Linien zu einander haben müssen, welche in Wirklichkeit rechtwinklig zu einander stehen, wie a und d oder e und f in Fig. 14, mit andern Worten, nach welcher Regel der Fluchtpunkt einer verkürzten wagrechten Linie zu bestimmen ist, welche zu einer gegebenen Wagrechten geometrisch rechtwinklig steht.

Rechtwinklige wagrechte Linien.

§ 32. Man unterscheidet die gerade Ansicht eines rechten Winkels, Rechtecks oder Quadrats, d. i. wenn nur eine der beiden Linien, welche einen rechten Winkel bilden, verkürzt, die andere aber unverkürzt ist, wie A B und B C oder A D und D C in Fig. 25 und die schräge Ansicht, d. i. wenn beide Schenkel des Winkels verkürzt sind, wie a b und b c oder a d und d c. Der Ausdruck »schräg« bezieht sich also in diesem Zusammenhang auf die Stellung wagrechter Linien zum Auge oder zum Horizont.

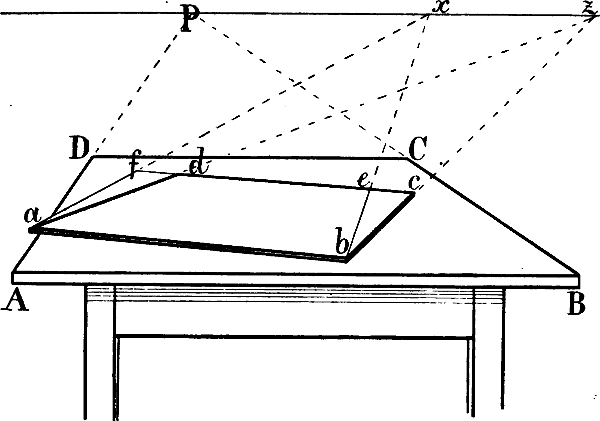
In § 12 Fig. 15 und 16 wurde gezeigt, dass eine vom Auge nach dem Augpunkt gezogene Linie einen rechten Winkel zum Horizont bilden würde, d. h. mit andern Worten: wenn wir uns eine Linie von unserem Auge nach dem Horizont gezogen denken, so dass sie rechtwinklig zu diesem steht, so trifft sie den Augpunkt, der Augpunkt ist ihr Fluchtpunkt.

Steht nun eine verkürzte wagrechte Linie geometrisch rechtwinklig zu einer unverkürzten Wagrechten, wie in Fig. 25 A D oder B C zu C D, so steht sie auch zum Horizont in einem rechten Winkel, sie ist also parallel mit einer von unserem Auge nach dem Augpunkt gehenden Linie und muss mit dieser denselben Fluchtpunkt haben.

Also ist der Augpunkt der Fluchtpunkt aller verkürzten wagrechten Linien, welche zu einer[38] unverkürzten Wagrechten (zum Horizont) geometrisch rechtwinklig stehen oder welche, wie man häufig sagt, sich in gerader Linie von uns entfernen. Vgl. in Fig. 14 die Linien f, f, in Fig. 20 a P, b P, c P u. s. w.

§ 33. Sind beide Linien, welche den rechten Winkel bilden, verkürzt, wie in dem Rechteck a b c d Fig. 25, so ist die Frage, wie gross die Entfernung der beiden Fluchtpunkte von einander, d. h. das Stück des Horizonts, welches zwischen beiden liegt, sein muss. Denn je nachdem der Winkel, in welchem 2 verkürzte Linien zu einander stehen, grösser oder kleiner ist, wird auch die Entfernung ihrer beiden Fluchtpunkte eine grössere oder kleinere sein und umgekehrt, wie aus § 31 Fig. 23 zu ersehen ist.

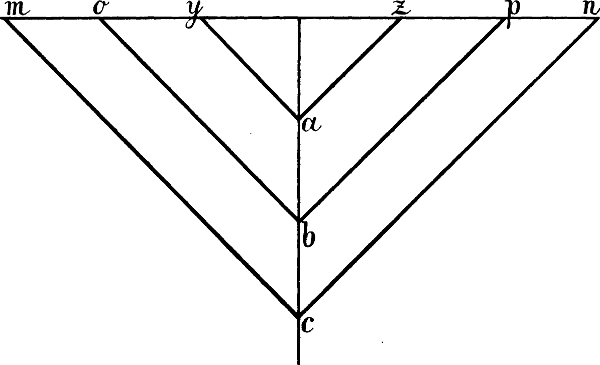
Ausser der geometrischen Grösse des betreffenden Winkels ist jedoch auch die Grösse der Distanz von Einfluss auf den Abstand der Fluchtpunkte seiner beiden Schenkel. Eine vom[39] Auge nach dem Horizont gezogene Linie, welche zu diesem rechtwinklig steht, trifft immer den Augpunkt und so kann auch die verkürzte Seite eines rechten Winkels in gerader Ansicht nur im Augpunkt ihren Fluchtpunkt haben, gleichviel, ob unsere Distanz grösser oder kleiner ist. Steht aber eine verkürzte Wagrechte in einem beliebigen andern Winkel zum Horizont oder zu einer unverkürzten Wagrechten, so liegt der Punkt, in welchem eine parallel mit ihr d. h. in demselben Winkel vom Auge nach dem Horizont gezogene Linie diesen treffen würde, näher am Augpunkt oder entfernter von ihm, je nachdem die Entfernung des Auges vom Augpunkt grösser oder kleiner ist. Dieselbe Linie, welche in Fig. 26 von a aus gezogen die Linie m n in z trifft, trifft sie von b aus in p, von c aus in n u. s. w. Und wenn wir 2 verkürzte wagrechte Linien vor uns haben, welche in Wirklichkeit rechtwinklig (oder in einem beliebigen Winkel) zu einander stehen, so werden die 2 Punkte, in welchen 2 parallel mit ihnen vom Auge ausgehende[40] Linien den Horizont treffen, desto näher beisammen liegen, je kleiner die Distanz ist und desto weiter von einander entfernt sein, je grösser dieselbe ist, wie Fig. 26 deutlich zeigt: o p ist grösser als y z, m n grösser als o p.

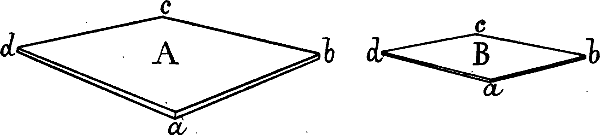
Demnach kann der Abstand der beiden Fluchtpunkte eines rechten Winkels in schräger Ansicht ein sehr verschiedener sein. So zeigt Fig. 27 zwei verschiedene Ansichten eines Rechtecks, welche es in derselben Stellung, aus derselben Höhe und Richtung, aber aus verschiedener Entfernung gezeichnet darstellen. Mit zunehmender Distanz erscheint nicht nur das Ganze kleiner, sondern auch die Form der rechten Winkel wird eine verschiedene: da mit der Distanz die Entfernung der beiden Fluchtpunkte von einander zunimmt, so erscheinen die Seitenwinkel bei b und d in B spizer, der Winkel bei a und c erscheint stumpfer als in A.

Natürlich ist die Wirkung dieselbe, wenn wir, statt die Entfernung unseres Standpunkts zu verändern, den betreffenden Gegenstand näher oder ferner rücken, vgl. Fig. 29.

Es muss daher die genaue Grösse der für eine Zeichnung angenommenen Distanz mittels eines Distanzpunkts angegeben und dieser zu Hilfe genommen werden, wenn der Abstand jener 2 Fluchtpunkte von einander genau berechnet werden soll. Wie lezteres geschehen kann, ist in § 81–85 gezeigt. Da jedoch die Grösse der vom Zeichner angenommenen Distanz mit blossem Auge aus den Linien einer Zeichnung nicht zu ersehen ist, so kann gewöhnlich diese genauere Berechnung entbehrt und durch Beobachtung der nachfolgenden Regel ersezt werden.

§ 34. Überall, wo die Grösse der Distanz von wesentlichem Einfluss ist auf die perspectivische Form, kommt es hauptsächlich darauf an, die falsche Wirkung zu vermeiden, welche aus einer zu klein angenommenen Distanz entsteht. Bei Darstellung eines rechten Winkels in schräger Ansicht entsteht diese falsche Wirkung, wenn die Entfernung der beiden Fluchtpunkte von einander zu klein ist.

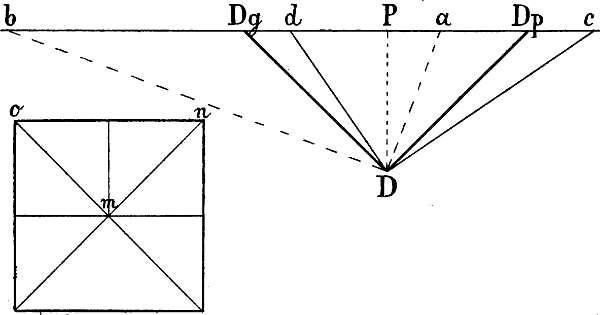
Betrachten wir in Fig. 28 D als unser Auge, P als Augpunkt, so bezeichnet die Linie D P die Grösse der Distanz. Ziehen wir nun (mit Hilfe des Winkels Fig. 9) von D aus in verschiedener Richtung je 2 rechtwinklig zu einander stehende Linien nach der durch P gehenden Wagrechten d. h. nach dem Horizont, z. B. D c und D d, D a und D b, D Dg und D Dp, so ergibt sich, dass die 2 Punkte, in welchen die verschiedenen Linienpaare den Horizont treffen, dann den geringsten Abstand von einander haben, wenn sich die beiden Linien in der Stellung zum Horizont befinden, welche D Dg und D Dp zeigen. Diese stehen zum Horizont, wie die Diagonalen eines Quadrats zu dessen Seiten, wie m n und m o zu o n, d. h. beide stehen[42] in einem halben rechten Winkel zum Horizont. Dg und Dp sind Diagonalpunkte: ihre Entfernung vom Augpunkt ist gleich der Distanz und ihre Entfernung von einander doppelt so gross als die Distanz, Dg–Dp ist gleich 2 mal Dp.

Bei jeder andern Stellung der beiden Linien zum Horizont ist der Abstand jener beiden Punkte ein grösserer und er wird immer grösser, je ungleicher die Stellung der beiden Linien zum Horizont ist: c d ist grösser als Dp–Dg, a b grösser als c d u. s. w.

§ 35. Hieraus folgt, dass die 2 Fluchtpunkte eines rechten Winkels in schräger Ansicht wenigstens so weit von einander entfernt sein müssen, dass der zwischen ihnen liegende Teil des Horizonts doppelt so gross ist, als die Distanz. Diese muss nach § 18 wenigstens doppelt so gross sein, als eine Diagonale des Bildes, oder als eine Linie vom Augpunkt nach dem von ihm entferntesten Punkte, also muss, wenn beide Schenkel eines aus 2 wagrechten Linien bestehenden rechten Winkels verkürzt sind, die Entfernung ihrer Fluchtpunkte von einander wenigstens 4 mal so gross sein, als eine Linie vom Augpunkt nach dem von ihm entferntesten Punkte der Zeichnung. Z. B. in Fig. 31 müssen, wenn A B und A C geometrisch rechtwinklige Linien sind, P Augpunkt und f die von P entfernteste Ecke des Bildes ist, die Fluchtpunkte der beiden genannten Linien einen Abstand von einander haben, der wenigstens = 4 mal P f ist.

Kommen in demselben Bilde verschiedene rechte Winkel in schräger Stellung vor, so müssen sie selbstverständlich in übereinstimmender Weise behandelt, d. h. es muss überall dieselbe Distanz zu Grunde gelegt werden.

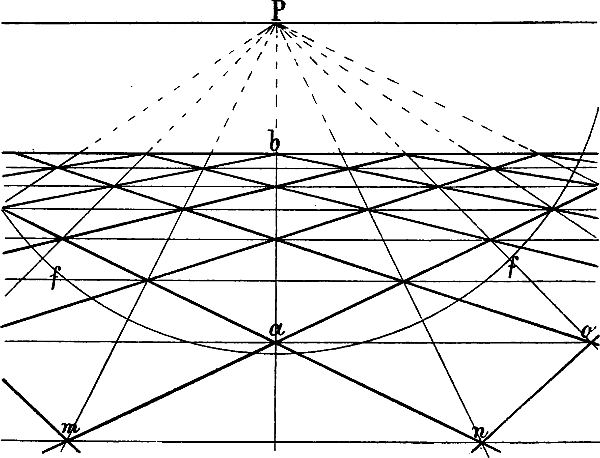
Die falsche Wirkung, welche entsteht, wenn gegen jene Regel gefehlt wird, zeigt Fig. 29. Die Entfernung der beiden Fluchtpunkte von einander ist = 4 mal P f; daher wirken alle[43] rechten Winkel, welche innerhalb der Kreislinie f f liegen, perspectivisch richtig, aber die Winkel bei m, n und o können nicht mehr als rechte Winkel gelten.

Andererseits zeigt Fig. 25, dass dem Zeichner innerhalb der angegebenen Grenze einige Freiheit gestattet ist: a b e f wird auch dem geübtesten Auge ebenso als richtiges Bild eines Rechtecks erscheinen, wie a b c d.

§ 36. Allerdings ist nicht sofort ersichtlich, wie gross die Entfernung der beiden Fluchtpunkte ist oder sein muss, da niemals beide innerhalb der Zeichnung, häufig dagegen weit ausserhalb derselben liegen. Will man sich nicht mit der Aushilfe begnügen, welche § 27 in Betreff entfernter Fluchtpunkte angegeben wurde, so ist in Fig. 30 eine genauere Berechnung gezeigt. A B und A C seien 2 verkürzte wagrechte Linien. Eine von A zum Horizont gezogene Senkrechte A P ist in[44] 4 gleiche Teile geteilt und vom oberen Teilungspunkt a sind 2 Linien a b und a c geometrisch parallel mit A B und A C gezogen, indem an beliebigen Punkten der lezteren Linien z. B. in D und E 2 Senkrechte errichtet und D d und E e = A a gemacht wurden. c b kann nun als ein Viertel des Abstandes betrachtet werden, welchen die Fluchtpunkte der Linien A B und A C von einander haben und es lässt sich hienach bemessen, ob derselbe hinreichend gross ist. Wäre z. B. f der von P entfernteste Punkt der Zeichnung, so dürften die beiden Linien A B und B C nicht stärker als hier der Fall ist gegen einander geneigt sein, der Abstand ihrer Fluchtpunkte dürfte nicht kleiner sein als 4 mal c b; denn c b ist = P f.

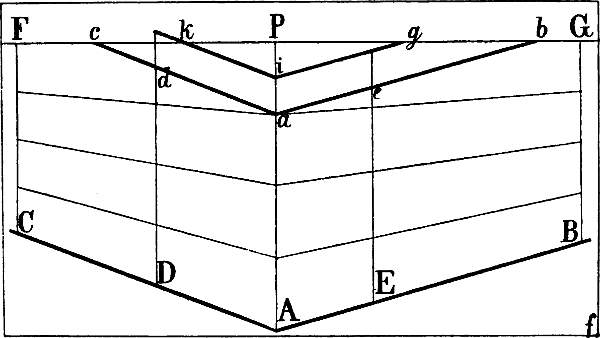
Oder: wenn A B als erste Linie gezeichnet ist, so muss, nachdem a b parallel mit A B gezogen und b c = P f gemacht ist, die zweite von A ausgehende Linie entweder parallel mit a c oder nach einem ferner liegenden Fluchtpunkt gerichtet sein, d. h. eine flachere Richtung haben, als A C.

Würden bei einer Vierteilung der erstgenannten Senkrechten nicht beide den Punkten b und c entsprechenden Punkte[45] innerhalb der Zeichnung fallen, so halbiere man das dem Horizont zunächst liegende Viertel und ziehe von hier aus die beiden Linien nach dem Horizont, also i g und i k statt a b und a c. Die Punkte, wo sie den Horizont treffen, hier g und k, müssen in diesem Fall einen Abstand haben, der wenigstens halb so gross ist, als eine Linie vom Augpunkt nach dem von ihm entferntesten Punkte.

Verkürzte wagrechte Linien, deren Richtung nicht genau zu berechnen ist.

§ 37. Wo die perspectivische Richtung einer verkürzten wagrechten Linie ohne genauere Berechnung gefunden werden muss, bietet die Vergleichung mit einer unverkürzten Wagrechten das beste Mittel, um den Grad, in welchem jene nach dem Horizont hin fallen oder steigen muss, richtig zu beurteilen. Man halte zu diesem Zweck den Rand des Zeichenblattes, ein Lineal oder dergl. in der Richtung einer unverkürzten Wagrechten so zwischen Auge und Gegenstand, dass ein Endpunkt der verkürzten Linie, welche man zeichnen will, davon durchschnitten wird, wie in Fig. 34 der Punkt a von der Linie e f. Übrigens ist auch die perspectivische Länge einer verkürzten Linie von wesentlichem Einfluss auf die richtige oder unrichtige Wirkung ihrer perspectivischen Richtung. Je weniger die Stellung einer verkürzten Wagrechten zum Horizont von der Richtung des lezteren abweicht, desto weniger verändert sich ihr Grössenverhältnis zu andern Linien; je mehr sie der rechtwinkligen Stellung zum Horizont, ihr Fluchtpunkt dem Augpunkt sich nähert, desto kürzer scheint sie zu werden, vgl. Fig. 23. Es kommt nun häufig vor, dass die perspectivische Richtung verkürzter Linien, wenn sie ganz der Regel entsprechend angegeben ist, dennoch eine falsche Wirkung macht, weil ihr perspectivisches Grössenverhältnis verfehlt ist und zwar geschieht dies gewöhnlich in der Weise, dass sie zu lang gezeichnet wird (vgl. § 7).

Wagrechte Parallellinien, deren Fluchtpunkt unzugänglich ist.

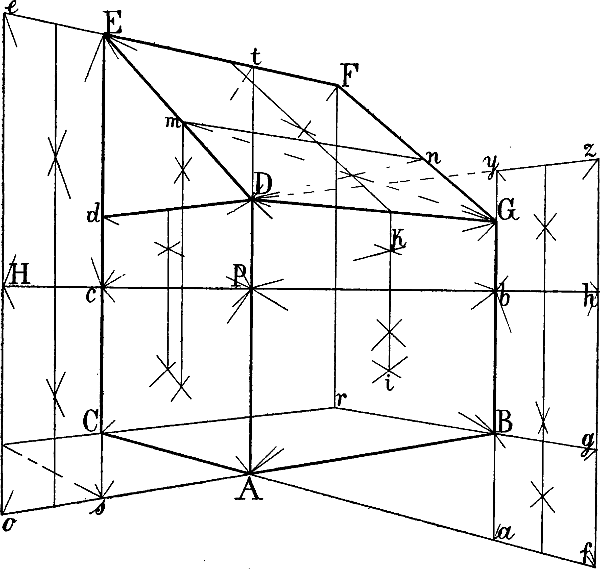
§ 38. In Fig. 31–33 ist gezeigt, wie die Richtung verkürzter wagrechter Parallellinien, deren Fluchtpunkt nicht erreichbar ist, genau berechnet werden kann. Es seien in Fig. 31 gegeben die Wagrechten A B und A C sowie die Senkrechten A D und C E und sollen von D und E Linien parallel mit A B, von D und B 2 weitere parallel mit A C gezeichnet[47] werden. Man bilde über A B mit der Horizontlinie und einer in B errichteten Senkrechten das Rechteck A B b P und errichte in i, dem Schnittpunkt seiner Diagonalen, eine Senkrechte, ziehe hierauf eine Linie von D nach b und von P durch den Punkt k, in welchem D b jene Senkrechte schneidet, eine Linie nach der verlängerten B b, so ist D G perspectivisch parallel mit A B.

Ebenso ist auf der andern Seite durch die Diagonalen des Rechtecks A C c P dessen perspectivischer Mittelpunkt gefunden und eine in diesem errichtete Senkrechte benüzt, um die Lage des Punktes d und hiemit die Richtung der mit A C parallelen Linie D d zu bestimmen.

Um von E eine mit A B parallele Linie zu zeichnen, kann leztere bis zu der durch E gehenden Senkrechten also bis s verlängert und die perspectivische Mittellinie des Rechtecks s A P c wie oben benüzt werden, um den Punkt t zu erhalten. Oder kann seitwärts ein Rechteck s o H c gebildet, mittels seiner senkrechten Halbierungslinie oben der Punkt e gefunden und hierauf e E nach rechts verlängert werden.

Wie auf gleiche Weise die mit A C parallele Richtung der von B ausgehenden Linie B g und damit B r mittels der Halbierungslinie eines Rechtecks b a f h gefunden wird, ist aus den Linien der Figur zu ersehen. Statt der Linie A C könnte auch eine andere mit ihr parallele Linie z. B. d D verlängert und durch die Diagonalen y h und z b die Mittellinie von b h z y gefunden werden.

Um schliesslich den Punkt F zu erhalten, kann von C eine mit A B parallele Linie gezeichnet und in dem Punkte r, in welchem sie die verlängerte B g trifft, eine Senkrechte errichtet werden, welche die parallel mit A B von E ausgehende Linie in F schneidet.

Ist so das schräg liegende Rechteck E D G F gegeben, so lässt sich die schräge Mittellinie desselben (welche sich durch Verbindung des perspectivischen Halbierungspunktes von D G mit dem Schnittpunkt der Diagonalen D F und E G ergibt)[48] verwenden, um von einem beliebigen Punkte der Linien D E oder G F eine mit D G parallele Linie zu ziehen, z. B. m n.

§ 39. In Fig. 32 sollen, nachdem A B und A C als Seiten eines Rechtecks gegeben sind, die beiden andern Seiten gezeichnet werden. Da der Raum nicht gestattet, die genannten Linien wie in Fig. 31 bis zu den 2 von C und B abwärts gezogenen Senkrechten zu verlangen, so sind A a, B b und C c halbiert und durch die Halbierungspunkte die Linien g f e und h f k gezogen, welche perspectivisch parallel sind mit A B und A C. Entsprechend § 38 ist nun eine Senkrechte durch i, den Schnittpunkt der Diagonalen a e und c f gezogen, welche von der Linie f C in m geschnitten wird. Eine Linie von e durch m ergibt auf der Senkrechten A a den Punkt p und die mit A B parallele Richtung C p. In gleicher Weise ist die mit A C parallele Richtung B o durch die senkrechte Mittellinie[49] des Rechtecks a b k f gefunden; statt dessen könnte auch, wie die Figur zeigt, ein seitwärts gebildetes Rechteck zu demselben Zweck verwendet werden.

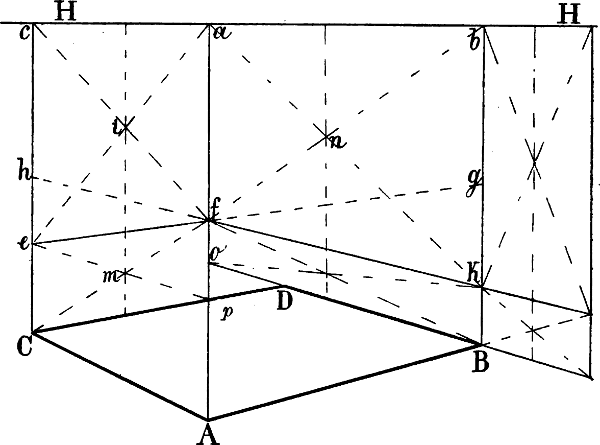
Bequemer wäre jedoch in diesem Fall das in Fig. 33 angewendete Verfahren, wo gleichfalls A B und A C die gegebenen Seiten eines zu bildenden Rechtecks sein sollen.

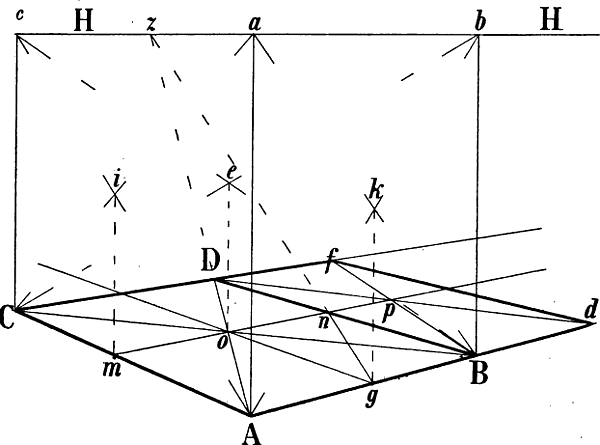
Wenn in einem von 6 Quadraten oder Rechtecken umschlossenen Raume zwischen 2 entgegengesezten Ecken Diagonallinien gezogen werden, wie in Fig. 40 die Linien a b und B c, so schneiden sich dieselben in der Mitte jenes Raums: p Fig. 40 ist die Mitte von A B b C c a G h. Eine durch p gezogene Senkrechte trifft also die Rechtecke a G h c und A B b C in dem Durchschnittspunkt ihrer Diagonalen. Ziehen wir nun in Fig. 33 von A, B und C bis zum Horizont die Senkrechten A a, B b und C c, so entsprechen die Linien B c und C b,[50] welche sich in e schneiden, den Diagonalen B c und a b Fig. 40 und eine von e abwärts gezogene Senkrechte ergibt o als perspectivische Mitte der Diagonale C B. Die Diagonalen A b und a B schneiden sich in k, A c und a C in i; g und m sind also die perspectivischen Halbierungspunkte von A B und A C; z ist Fluchtpunkt der Diagonale A o und folglich auch der von g nach der Mitte von B D gehenden Linie, da beide geometrisch parallel sind. g z und die verlängerte m o schneiden sich in n, A z und die verlängerte B n in D, womit die Form des Rechtecks gegeben ist.

Die verlängerten Mittellinien m n und g o können sodann benüzt werden, um entsprechend Fig. 31 und 32 weitere mit A B und A C parallele Linien zu ziehen. Soll z. B. von d nach links eine mit A C parallele Linie gezeichnet werden, so schneidet man die verlängerte m n durch D d in p und zieht von B durch p eine Linie nach f; d f ist somit parallel mit A C und B D.

§ 40. Muss eine grössere Anzahl von Parallellinien, deren Fluchtpunkt unzugänglich ist, gezeichnet werden, so würde es zu umständlich sein, jede einzelne genau zu berechnen. Man kann sich in diesem Fall begnügen, einige in passenden Zwischenräumen zu konstruieren, um mit Hilfe derselben ohne weitere Berechnung die übrigen zu zeichnen. So können in Fig. 21, wenn die Richtung c d gegeben ist, mittels der senkrechten Halbierungslinie von c d e f die von g, h und i ausgehenden Parallellinien genau berechnet und sodann die zwischen ihnen liegenden ohne weitere Berechnung gezeichnet werden.

Oder können von 2 beliebigen Punkten der zuerst gezeichneten Wagrechten 2 Senkrechte bis zum Horizont gezogen und beide in eine gleiche Zahl von gleich grossen Teilen geteilt werden wie in Fig. 30 A P, B G und C F in je 4 Teile geteilt sind. Durch die Verbindung der entsprechenden Teilungspunkte erhält man perspectivische Parallellinien, zwischen welchen dann weitere gezogen werden können, vgl. Fig. 75 die Teilung[51] von A D und B C in je 9 Teile. Je nach Bedürfnis kann sodann dieselbe Einteilung nach oben oder unten in der Verlängerung jener Senkrechten fortgesezt werden.

Ein weiteres Verfahren, die Richtung verkürzter Parallellinien ohne Hilfe ihres Fluchtpunkts zu bestimmen, ist in § 70 angegeben.

Verkürzte schräge Linien.

§ 41. In Fig. 36 ist a c eine nach der Ferne hin steigende, a g eine dorthin fallende Linie. (Wenn im Folgenden von fallenden oder steigenden Linien die Rede ist, so sind immer Linien gemeint, welche in Wirklichkeit oder geometrisch nach der Ferne hin fallen oder steigen). Bilden wir das Massdreieck dieser Linien (vgl. § 23) mittels der Wagrechten a b und der 2 Senkrechten b c und b g, so ist klar, dass eine steigende Linie wie a c, soweit man sie verlängern mag, niemals einen Punkt treffen kann, der unterhalb der wagrechten Linie ihres Massdreiecks oder deren Verlängerung liegt und ebenso wenig eine fallende Linie wie a g einen Punkt, der über jener Wagrechten liegt.

Also liegt der Fluchtpunkt einer verkürzten schrägen Linie oberhalb des Horizonts, wenn sie nach der Ferne hin steigt, unterhalb des Horizonts, wenn sie nach der Ferne hin fällt; vgl. die steigenden und fallenden Linien in Fig. 37.

§ 42. Es kann vorkommen, dass gemäss dieser Regel eine steigende Linie so gezeichnet werden muss, dass ihr fernerer Endpunkt tiefer liegt als der nähere, vgl. a c Fig. 34. Häufiger ist der umgekehrte Fall, dass Linien, welche in Wirklichkeit nach der Ferne hin fallen, perspectivisch nach dorthin steigen, wie a b und c d Fig. 35.

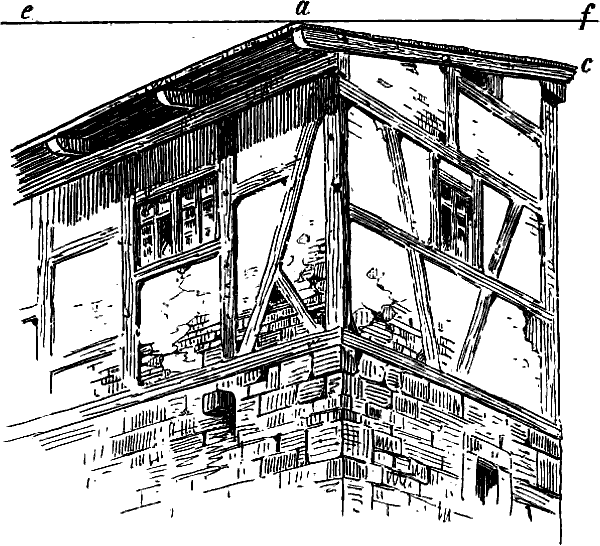
In solchen Fällen ist es nötig, durch Hervorheben von geometrisch wagrechten Linien der nächsten Umgebung, welche[52] zu den betreffenden schrägen Linien einen sichtbaren Gegensaz bilden, die Wirkung der lezteren zu unterstüzen, damit sie mit hinreichender Deutlichkeit das ausdrücken, was sie sein sollen. In Fig. 34 sind es z. B. die Balken der rechten Seite, in Fig. 35 die wagrechten Fugenlinien der anstossenden Mauer, welche es dem Beschauer deutlich machen, dass a c dort eine in Wirklichkeit von a nach c steigende, a b in Fig. 35 eine nach b fallende Linie ist.

§ 43. In Fig. 36 sind a b und e f wagrechte Parallellinien, ebenso a e, b f und c d; a c und e d sind schräge Parallellinien. Wenn zwischen parallelen Linien Verbindungslinien[53] liegen, welche unter sich gleichfalls parallel sind, so sind leztere gleich lang (§ 1, Fig. 1); also sind a e, b f und c d gleich lang, d. h. die Entfernung der schrägen Parallellinien a c und e d und diejenige der wagrechten a b und e f von einander ist gleich gross. Da der Abstand dieser Parallellinien von einander nach der Ferne hin in gleichem Masse kleiner zu werden scheint, d. h. in gleicher Tiefe immer wieder derselbe ist – m n ist = o p u. s. w. – so müssen beide in gleicher Tiefe zusammentreffen, d. h. ihre Fluchtpunkte müssen in Einer senkrechten Linie liegen, wie Fig. 36 deutlich zeigt.

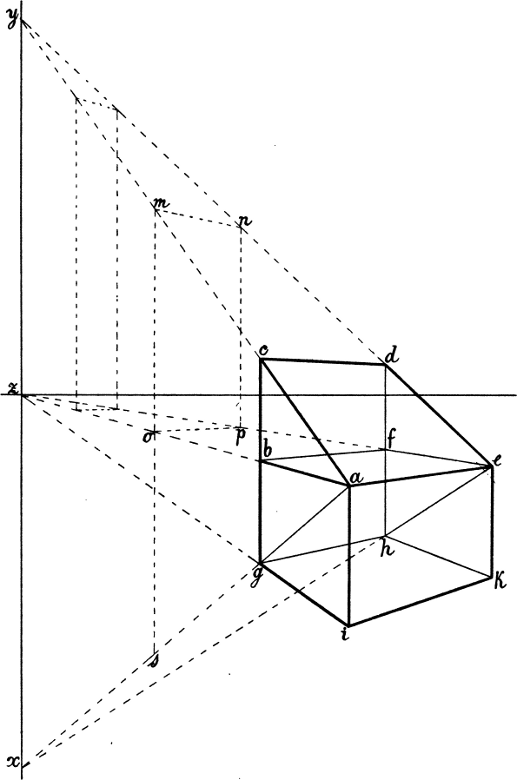
Dasselbe gilt selbstverständlich für die fallenden Linien a g und e h. Mit andern Worten: der Fluchtpunkt einer verkürzten schrägen Linie liegt senkrecht über oder unter dem Fluchtpunkt der wagrechten Linie ihres Massdreiecks.

So liegt in Fig. 37 der Fluchtpunkt der Linien a, b, c und d senkrecht über n, der Fluchtpunkt der Linien g und i senkrecht unter n, die Fluchtpunkte von e, f und k liegen in einer Senkrechten, welche durch den Fluchtpunkt der Wagrechten o und p geht.

Ist demnach a c Fig. 36 als Richtung einer schrägen Linie, a b als Richtung der wagrechten Linie ihres Massdreiecks angenommen, so ist auch die perspectivische Richtung aller mit a c parallelen Linien gegeben, indem a b bis zum Horizont, a c bis zu der senkrechten durch den Fluchtpunkt von a b gehenden Linie verlängert und so der die Richtung der parallelen Linien bestimmende Fluchtpunkt gefunden wird.

§ 44. Befinden sich in einer verkürzten senkrechten Fläche steigende und fallende Linien, welche in Wirklichkeit denselben Neigungswinkel haben, so liegen ihre Fluchtpunkte in gleicher Entfernung vom Horizont.

Solche Linien sind z. B. a c und a g Fig. 36; a und g, d und i, f und k Fig. 37. In Fig. 36 ist a c g in Wirklichkeit ein gleichschenkliges Dreieck, also muss eine von seiner Spize a nach der Grundlinie c g gezogene Wagrechte die leztere in ihrem Halbierungspunkt b treffen; werden a c und a g verlängert und an beliebiger Stelle durch eine Senkrechte s m verbunden, so wird leztere durch die verlängerte a b gleichfalls halbiert, also muss auch z, der Fluchtpunkt von a b, in der Mitte liegen zwischen x und y, den Fluchtpunkten von a g und a c.

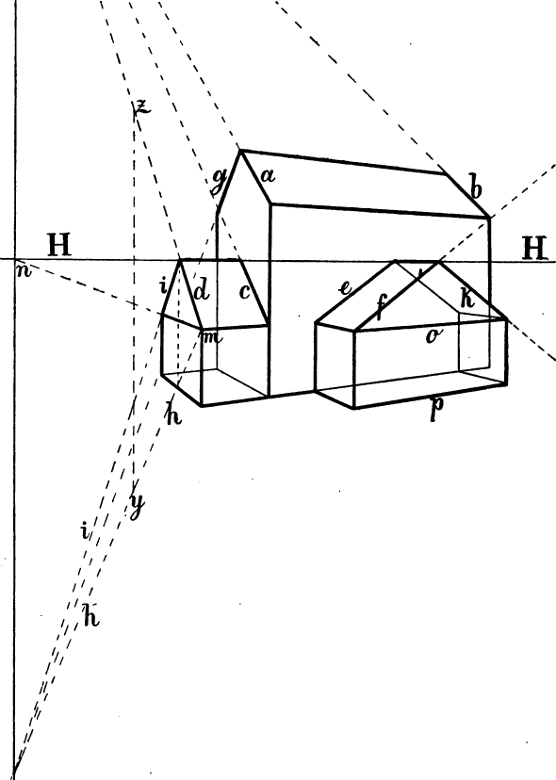
In Fig. 37 ist h h parallel mit i i (da beide denselben Fluchtpunkt haben) und die Senkrechte y z wird von der[57] Wagrechten m n in der Mitte durchschnitten. Ebenso muss n in der Mitte liegen zwischen den Fluchtpunkten der Linien h, i, g und c, d, a; die Fluchtpunkte von e, f und k müssen gleich weit entfernt sein vom Fluchtpunkt der Wagrechten o und p.

Berechnung der Richtung schräger Linien ohne Hilfe ihrer Fluchtpunkte.

§ 45. Man bedient sich jedoch, um die Richtung verkürzter schräger Linien zu berechnen, selten ihrer Fluchtpunkte, da dieselben in den meisten Fällen ausserhalb der Zeichenfläche liegen. Den nächstliegenden Ersaz bietet die senkrechte und wagrechte Linie ihres Massdreiecks. Ist Richtung und Länge der wagrechten sowie die Höhe der senkrechten Linie eines solchen Dreiecks gegeben oder leicht zu berechnen, so ist damit auch die Richtung (und Länge) der betreffenden schrägen Linien gefunden.

Nehmen wir z. B. an, dass in Fig. 38 die Linie A C gegeben sei und darüber ein Giebel von beliebiger Höhe, dessen 2 Seiten mit A C in Wirklichkeit ein gleichschenkliges Dreieck bilden, gezeichnet werden soll, so kann k als perspectivische Mitte von A C durch die Diagonalen eines Rechtecks A C E D oder A C g f gefunden und in k eine Senkrechte errichtet werden, in welcher die Spize des Giebeldreiecks liegen muss. – Ist das Dreieck A B k gegeben, so dass der Punkt C bestimmt werden muss, so bildet man mit A k und einer beliebigen Parallellinie, z. B. i D, ein Rechteck A k i D und zieht eine Linie von D durch die Mitte von i k nach der verlängerten A k, wodurch C k = A k gemacht ist.

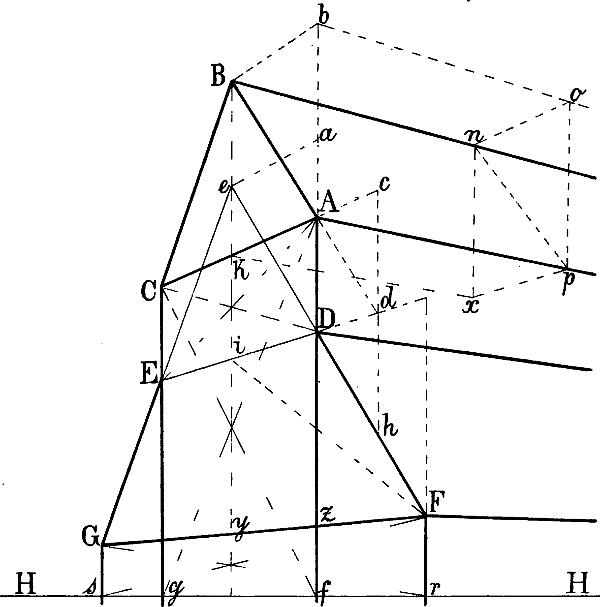
Soll, nachdem D F und D E gegeben sind, von E abwärts eine Linie gezeichnet werden, welche denselben Neigungswinkel hat, wie D F, so wird leztere verlängert bis e, wo sie die senkrechte Mittellinie trifft und von e durch E die Linie E G gezogen. – Oder kann von F eine mit D E parallele[58] Linie nach links und die senkrechte Mittellinie von E D f g gezogen, die von y nach H H gehende Senkrechte halbiert und hierauf durch eine Linie von r durch diesen Halbierungspunkt der Punkt G bestimmt werden.

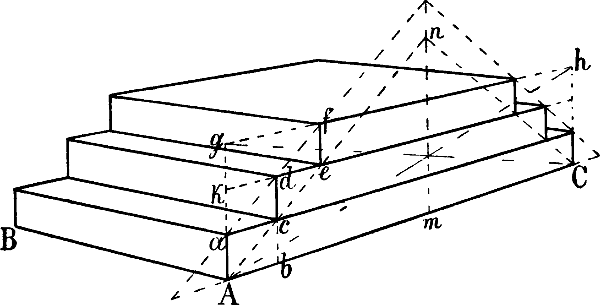
§ 46. In Fig. 39 ist angenommen, dass die perspectivische Richtung und Länge der Linien A B und A C, die Höhe A a und die Breite a c bestimmt seien, womit auch die Richtung der schrägen Linie A c gegeben ist, in welcher die inneren Ecken der Stufen liegen müssen; die äusseren Ecken liegen in einer mit A c parallel von a ausgehenden Linie, deren[59] Richtung gefunden wird, indem man c d = b c macht. Eine Linie von d nach dem Fluchtpunkt von A C ergibt e, eine Senkrechte von hier den Punkt f. Bildet man hierauf das Rechteck A C h g, so kann mittels seiner Diagonalen m n als senkrechte Mittellinie gefunden werden; C m n ist demnach = A m n und die Ecken der ferneren Stufen können durch die von a und k nach dem Fluchtpunkt von A C gezogenen Linien und die entsprechenden Senkrechten gefunden werden. (Übrigens kann dieselbe Aufgabe auch ohne Hilfe der zweiten schrägen Linie gelöst werden: man macht a k und k g = A a, zieht von diesen Punkten aus die mit A C parallelen Linien und erhält die Punkte d und f durch die in c und e errichteten Senkrechten.) Die übrigen Linien der Figur sind teils senkrecht, teils sind sie parallel mit A C oder mit A B.

§ 47. Ein Beispiel, wie die Richtung verkürzter schräger Parallellinien ohne Hilfe ihres Fluchtpunkts berechnet werden kann, ist auch in Fig. 31 enthalten, wo, um den Punkt F zu finden, B r und C r gezogen und in r eine Senkrechte errichtet wurde, welche auf der von E ausgehenden Wagrechten den Punkt F und hiemit die mit D E parallele Richtung der Linie G F ergibt. Auf dieselbe Weise kann in Fig. 40, wenn[60] das Dreieck A B D und die Wagrechte A C gegeben sind, die Richtung der mit A D parallelen Linie C E berechnet werden, indem man von C eine mit A B, von d und D zwei mit A C parallele Linien zieht und in e eine Senkrechte errichtet. Ebenso kann F n gefunden werden durch die Linien F m und m n.

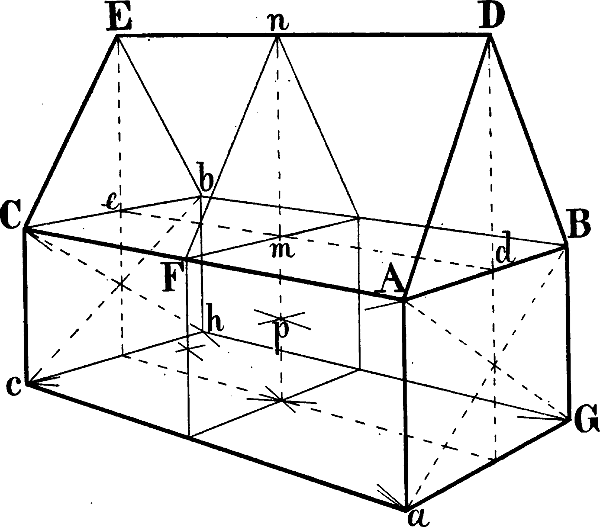
In Fig. 38 kann von p aus eine Linie parallel mit A B gezeichnet werden mittels der Linien k x, p x und einer in x errichteten Senkrechten. Oder kann man in A und p 2 Senkrechte errichten, B b parallel mit A C, b o parallel mit A p ziehen und hierauf durch eine weitere mit A C parallele Linie von o aus den Punkt n bestimmen.

Soll von D aus abwärts eine mit A B parallele Linie gezeichnet werden, so kann durch die Verlängerung von A B, A C und D E ein Dreieck A c d gebildet und d h = c d gemacht werden, wodurch D h parallel mit B A ist. Oder kann,[61] nachdem das Dreieck A B b gezeichnet ist, D a = A b gemacht und von a eine mit A C und b B parallele Linie bis zu der Senkrechten B k gezogen werden, wodurch e D parallel mit A B ist und von D aus verlängert werden kann. Es könnte ferner, wenn F z geometrisch = y z ist, durch den Halbierungspunkt von D z eine Linie von i nach der verlängerten y z gezogen werden.

§ 48. In Fig. 41 sei A G a und A o gegeben. Um die Richtung der parallel mit A a von B, i und o ausgehenden Linien zu berechnen, ist durch den Halbierungspunkt der Senkrechten n a eine mit A G parallele Linie nach f und von hier aus f g als wagrechte Mittellinie des Daches gezogen, welche nun ähnlich wie die Mittellinien in Fig. 31 benüzt werden kann, um zwischen A B und a p beliebige mit A a parallele Linien[62] z. B. B b, i k und o p zu zeichnen: man zieht a B und A r b, b i und B s k u. s. w. Die Richtung der Linie C c ist auf die in § 45 Fig. 38 angegebene Weise berechnet: d h ist = n a gemacht und von h eine Linie durch C nach der verlängerten m z gezogen. Der Punkt F ergibt sich durch eine parallel mit A G von E nach der Verlängerung von b B gezogenen Linie; eine Senkrechte von F abwärts schneidet die von c nach rechts gehende Wagrechte in e, womit E e gegeben ist.

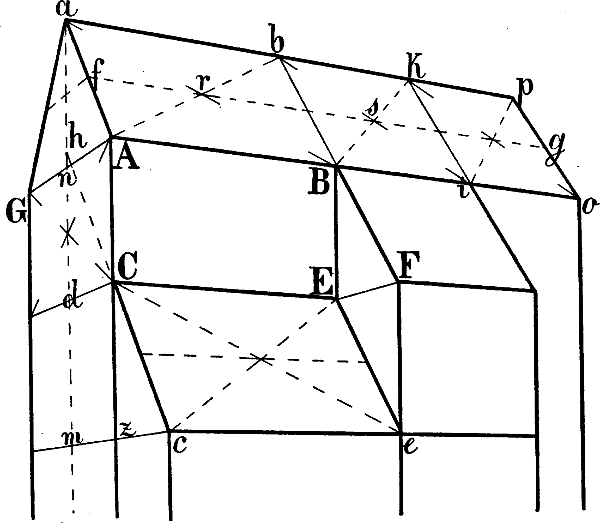
Sind auf solche Weise einige Parallellinien gezeichnet, so kann die perspectivische Richtung weiterer zwischen ihnen liegender Linien auch ohne genaue Berechnung jeder einzelnen ohne Schwierigkeit bestimmt werden.

Verschiedene Beispiele. Treppen, Dächer, Dachfenster, Turmhelme.

§ 49. Die Anwendung des vorangegangenen ist in Fig. 42–60 an weiteren Beispielen gezeigt. Der Gleichartigkeit des Gegenstands wegen befinden sich unter denselben auch solche, bei denen die im folgenden Abschnitt besprochene Form des verkürzten Quadrats als gegeben betrachtet werden muss.

Für die Construction der Treppe Fig. 42 nehmen wir die Höhe und Breite der untersten Stufe, also die perspectivische Länge der Linien B b und b c, sowie die Linie A B als gegeben an. Da leztere eine unverkürzte Wagrechte ist, so muss der Augpunkt Fluchtpunkt der Linie b c sein. Wird nun b m = B b gemacht, in c eine Senkrechte errichtet und von m eine Linie nach P gezogen, so ist c n die perspectivische Höhe der zweiten Stufe und es ist durch b n die Richtung der schrägen Linie gegeben, in welcher die vorderen Ecken der folgenden Stufen liegen müssen. Hierauf wird auf der verlängerten B m die Höhe B b mit dem Zirkel so oft wiederholt, als nötig ist, um die gewünschte Zahl von Stufen zu erhalten und werden von den Teilungspunkten Linien nach P gezogen.[63] Die Punkte, in welchen leztere die Linie b d schneiden, sind die vorderen Ecken der Stufen, die hinteren dem Punkte c entsprechenden Ecken ergeben sich durch die von o, p u. s. w. abwärts gezogenen Senkrechten. Auf der andern Seite schneiden sich a P und die von c nach links gezogene Wagrechte in y, eine Wagrechte von n nach links und eine in y errichtete Senkrechte schneiden sich in z u. s. w.

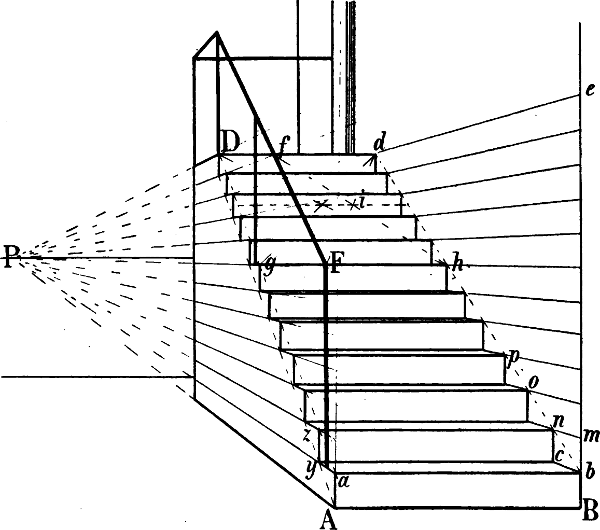
Um von F aus die mit a D und b d parallele Linie des Geländers zu zeichnen, ist durch die Diagonalen eines Rechtecks g h d D dessen wagrechte Mittellinie bestimmt, welche von der Linie F d in i geschnitten wird, worauf die von h durch i nach D d gezogene Diagonale den Punkt f und hiemit F f als Parallele von h d ergibt.

§ 50. Fig. 43 zeigt 2 häufige Formen von Dachfenstern. m y und n z sind parallel mit A D zu zeichnen, y z, o p, m n parallel mit A C; die Höhe m o sowie die Länge m y sind beliebig, vorausgesezt, dass o y und p z als nach y und z hin steigende Linien gezeichnet sind.

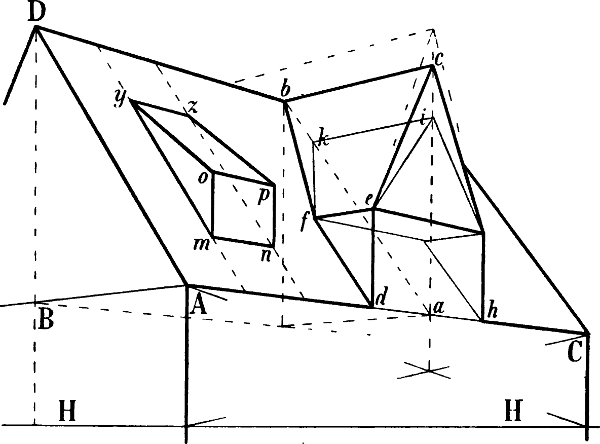
Bei der zweiten Form ist d f parallel mit A D; die Höhe des Giebels kann beispielsweise in i oder in c angenommen werden; e f, i k, c b sind parallel mit A B; die Punkte b oder k liegen sodann da, wo die von c oder i parallel mit A B gezogenen Wagrechten sich mit einer schrägen Linie schneiden, welche von a, der Mitte von d h, parallel mit A D aufsteigt. Durch den Punkt b, in welchem die leztgenannte Linie und die Firstlinie des Hauptdaches sich schneiden, ist c b als grösste Höhe gegeben, welche für die obere Wagrechte des Dachfensters angenommen werden darf, d. h. eine von seiner Giebelspize[65] parallel mit A B gezogene Wagrechte darf die von a parallel mit A D ausgehende Linie nicht jenseits des Punktes b, nicht oberhalb der Firstlinie D b treffen, es wäre denn, dass eine entsprechende Fortsezung auf der andern Dachseite angenommen würde.

§ 51. In Fig. 44 seien a b und b c als zwei Seiten eines quadratischen Turmes gegeben und soll darüber ein Dach gezeichnet werden, dessen Spize über der Mitte des ganzen Turmes, d. h. seiner quadratischen Grundfläche liegt. Zieht man die mit a b und b c parallelen Linien d c und a d, so muss die Spize in einer Senkrechten liegen, welche in dem Schnittpunkte der Diagonalen a c und b d errichtet wird; die Höhe der Spize ist beliebig. Bequemer wird in den meisten Fällen die Mitte des Ganzen auf die § 39 angegebene Weise gefunden: man zieht an beliebiger Stelle die mit a b und b c parallelen Linien e f und f g (oder benüzt statt derselben die Horizontlinie),[66] um mittels der Diagonalen c e und a g den gewünschten Punkt zu erhalten, in welchem jene Senkrechte zu errichten ist.

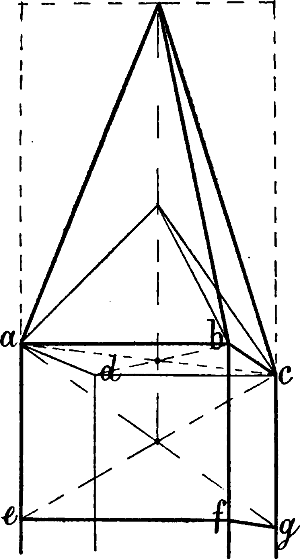
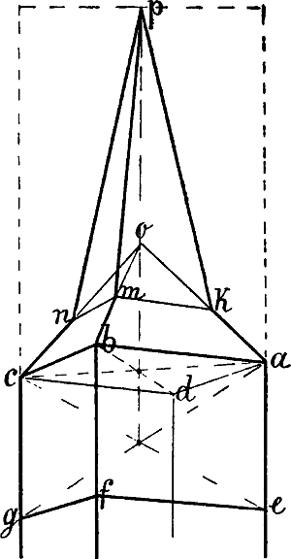
Häufig kann man sich auch damit begnügen, die 2 äusseren Senkrechten z. B. in Fig. 44 e a und g c, nach oben zu verlängern und die Spize in die Mitte zwischen beide zu verlegen. Das Resultat stimmt zwar nicht immer vollständig mit dem der genauen Berechnung überein, doch ist die Abweichung eine so geringe, dass die richtige Wirkung nicht dadurch beeinträchtigt wird; vgl. Fig. 45.

§ 52. In Fig. 45 sind zuerst von a, b und c aus 3 Linien nach einem tiefer liegenden Punkte o der senkrechten Mittellinie gezogen, hierauf an beliebiger Stelle die mit a b und b c parallelen Linien k m und m n und von den Punkten k, m und n 3 Linien nach der höher liegenden Spize p.

Die Construction von Fig. 46 ist hienach leicht zu verstehen. In Fig. 47 sind von a, b und c aus zuerst 3 Linien nach dem höher in der Mittellinie liegenden Punkt p, hierauf die mit a b und b c parallelen d e und e f, und nach dem tiefer liegenden Punkt o die Linien d o, e o und f o gezogen.

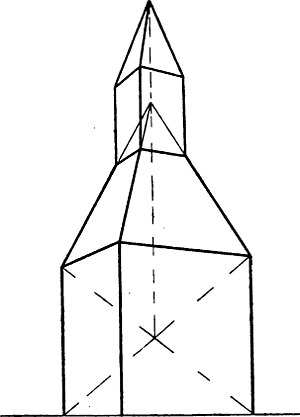
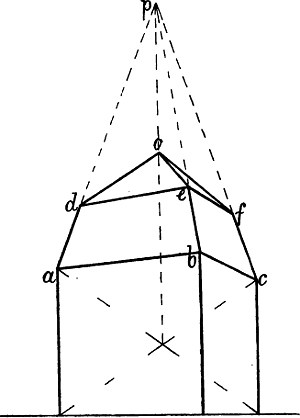
§ 53. Bei der in Fig. 48 und 49 dargestellten Dachform liegen die Punkte E und F senkrecht über den Punkten m und n, welche ihrerseits in der Mittellinie a b des Rechtecks A B C D liegen. m a ist in Wirklichkeit = n b; denken wir uns die senkrecht über A B und C D stehenden Giebelwände A B d und D C f hinzugezeichnet, so wäre auch E d = F f. Gewöhnlich haben die beiden schrägen Dreiecke (A B E und D C F) denselben Neigungswinkel wie die anstossenden Breitseiten des Daches. In diesem Fall müssen die senkrecht unter E und F liegenden Punkte m und n Mittelpunkte zweier Quadrate sein, deren Seiten = A B sind, so dass m a = A a wäre. Doch ist die Form auch dann eine richtige, wenn angenommen wird, dass der Neigungswinkel jener Flächen (A B E und A E F D) ein verschiedener sei. Die Hauptsache ist, dass E und F von d und f oder m und n von a und b gleich weit entfernt sind, mit andern Worten, dass die beiden Dreiecke A B E und C D F die gleiche Neigung haben. Zu diesem Zweck bestimme man in Fig. 48, angenommen, dass A B E und A D gegeben seien, die perspectivische Mitte der Firstlinie in h (mittels A C und B D oder B z und D y) bilde das Rechteck E h e c und ziehe c F durch die Mitte von h e, so ist F h perspectivisch = E h. Oder man verbinde (Fig. 49) den Halbierungspunkt r der Linie A D mit h, der wie oben gefundenen Mitte der Firstlinie, ziehe die Diagonale E D und durch den Punkt, in welchem E D und r h sich schneiden, eine Linie von A nach F.

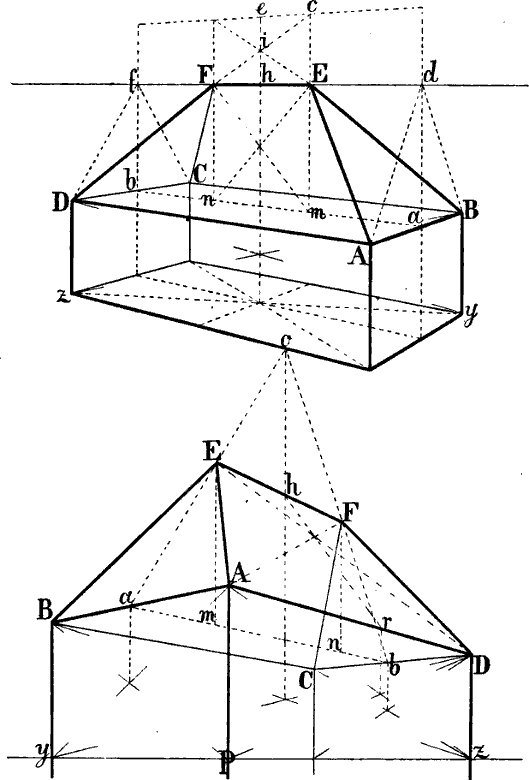
Oder auch man bestimme, nachdem A B E und A D (Fig. 49) gegeben sind, die perspectivische Mitte von A B und C D, also die Punkte a und b, ziehe von a durch E eine[69] Linie nach der senkrechten Mittellinie des Ganzen (errichtet im Schnittpunkte der Diagonalen B z und D y) und von o eine Linie nach b, welche die Firstlinie in F schneidet.

§ 54. Um das Dach Fig. 50 zu construieren, wird zuerst die einfache Dachform C A a g h und an beliebiger Stelle die Wagrechte e f parallel mit A a, sowie e c parallel mit A C gezeichnet. Die perspectivische Mitte von A C ist m, eine Linie von hier durch den Schnittpunkt i ergibt den Punkt n als Mitte der Firstlinie. Die Lage des einen der beiden Punkte D oder d wird beliebig angenommen, die des zweiten durch die Diagonalen D c und e d, wie in Fig. 49, § 53, gefunden.

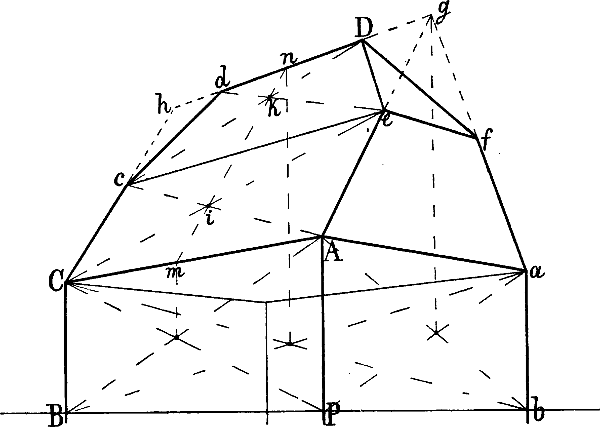
Häufig wird es auch genügen, bei Darstellung von Dachformen wie Fig. 48–50 zuerst die gewöhnliche Dachform mit senkrechten Giebelwänden oder die perspectivische Mitte der[70] Firstlinie anzugeben und nach dem Ermessen des Auges den ferneren der beiden geometrisch gleich grossen Teile kleiner zu zeichnen, als den näheren, also z. B. in Fig. 50 dafür zu sorgen, dass n d kleiner sei als D n, d h kleiner als g D.

§ 55. Wenn in einem Dach von der Fig. 48–50 dargestellten Form Dachfenster wie in Fig. 43 gezeichnet werden sollen, so muss die schräge Mittellinie der betreffenden Seite gesucht werden. In Fig. 51 z. B. muss die Linie e d perspectivisch parallel sein mit c D; wäre das Dachfenster nicht in der Mitte von A B D, so müsste eine mit c D parallele Linie entsprechend der Linie a b in Fig. 43 gezeichnet und sodann wie dort weiter verfahren werden.

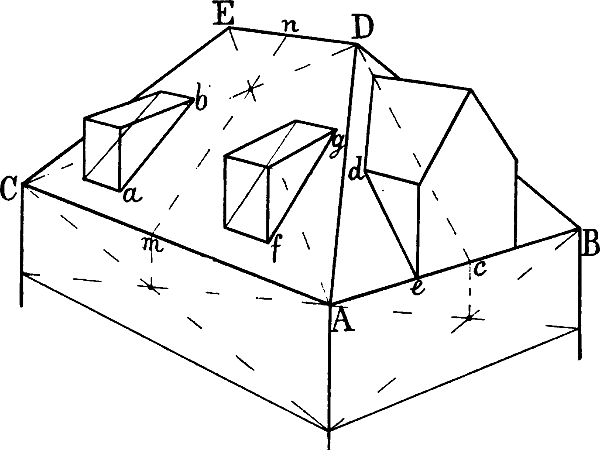
Auf der anstossenden Seite A C E D müssen a b, f g u. s. w. parallel sein mit der Mittellinie m n. In Fig. 53 wäre f c am unteren, c z am oberen Teil massgebend für die schrägen Linien eines Dachfensters.

§ 56. Fig. 52, ein Staffelgiebel, ist so construiert, dass zuerst die einfache Dachform a b c g e und die parallel mit a c von f und d ausgehenden Linien gezeichnet wurden (d g kleiner als f c). Um die Höhe der einzelnen Absäze zu bestimmen, ist in k eine über a hinausreichende Senkrechte k z errichtet und in die erforderliche Anzahl von gleichen Teilen geteilt. Durch die Teilungspunkte sind die Linien m n, o p u. s. w. und nach dem Fluchtpunkt der andern Seite m i, o h u. s. w. gezogen. Das Weitere ist aus den Constructionslinien der Fig. 52 leicht zu ersehen.

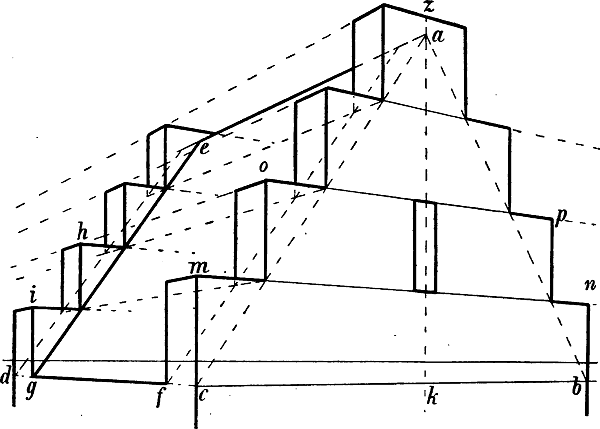
§ 57. Die Form eines Mansardendaches Fig. 53 ist stets eine solche, dass die 4 Seiten des unteren und ihrerseits diejenigen des oberen Teiles denselben Neigungswinkel haben. Es muss daher, wenn A B und A C gegeben sind, von A C ein Teil A f abgeschnitten werden, welcher perspectivisch = A B[72] ist, so dass die senkrechte Linie, in welcher die Punkte k und d liegen müssen, über der Mitte eines Quadrats (A B p f) oder über dem Schnittpunkt der Diagonalen B m und f n errichtet werden kann. Nachdem nun A a, a b, B b, a d und b d gezeichnet sind (vergl. § 52, Fig. 47), so werden die von a, d und k parallel mit A C ausgehenden Linien gezogen; i ergibt sich auf die § 53, Fig. 48 gezeigte Weise (nachdem z als Mitte der Firstlinie bestimmt ist), e durch eine von i abwärts gezogene Senkrechte, g durch eine Linie von i nach C.

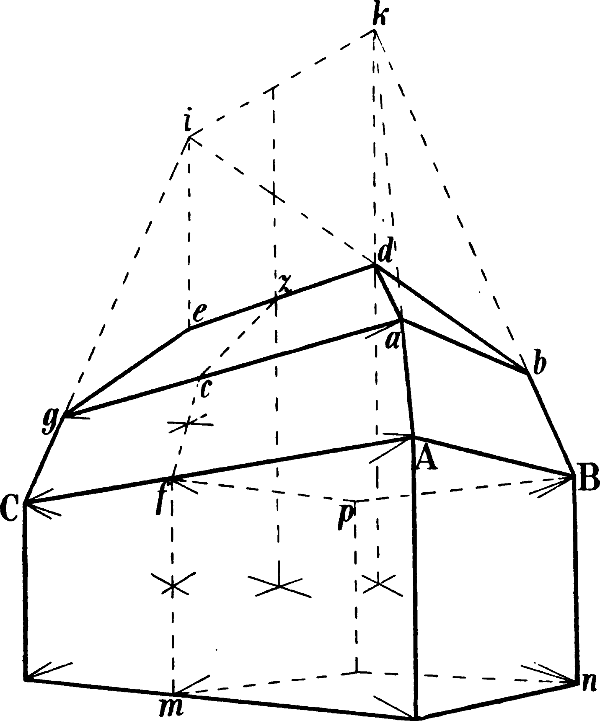
§ 58. Der Turmhelm Fig. 54 und 55 ist eine an Bauten des romanischen Stils häufige Form: die 4 Seiten des quadratischen Turms schliessen oben mit 4 Giebeln ab, von deren Spizen 4 Linien nach der Turmspize gehen und so mit den Giebellinien 4 rautenförmige Flächen bilden. Zunächst müssen die Giebelspizen in gleicher Höhe liegen; angenommen, dass in Fig. 54 a b d und a c gegeben seien, so können die senkrechten Ecklinien von a und b nach oben verlängert werden, bis sie eine parallel mit a b durch d gezogene Wagrechte treffen; eine Wagrechte von g aus parallel mit a c und eine Senkrechte über der perspectivischen Mitte von a c ergeben sodann den Punkt f, eine gleichfalls mit a c parallele Linie von h und eine mit a b parallele Linie von f aus den Punkt e (vergl. Fig. 56).

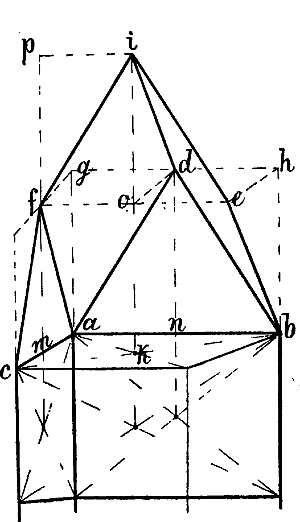
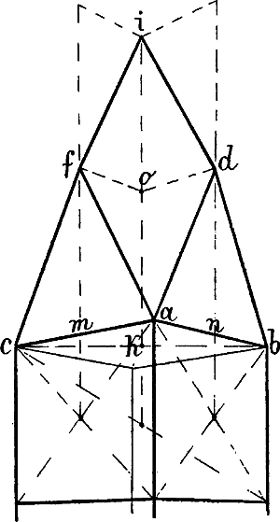
In Fig. 55 ist die Stellung des Turmes eine solche, dass nur eine der oberen 4 Flächen und keine der Umrisslinien des[74] dritten Giebelfeldes zu sehen ist. Die Höhe des zweiten Giebels ist hier dadurch gefunden, dass, nachdem a c f und die Linie a b gezeichnet waren, von f eine mit a b parallele Wagrechte bis zur senkrechten Mittellinie des ganzen Turmes, d. h. bis o und von hier eine mit a c parallele Linie bis zu der in der Mitte von a b errichteten Senkrechten gezogen wurde, wodurch d als Spize des rechtseitigen Giebels gegeben ist.

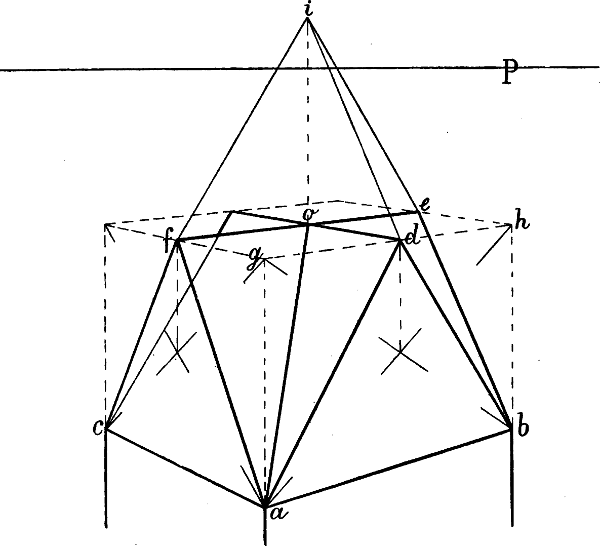
So könnte auch in Fig. 54 statt der oben angewendeten Construction von d eine mit a c parallele Wagrechte nach der senkrechten Mittellinie, durch den so gewonnenen Punkt o eine mit a b parallele Linie und hierauf b e perspectivisch parallel mit a f gezogen werden (vergl. Fig. 56).

Ferner muss, damit a i eine gerade Linie, a d i f eine Fläche sei, a d und a f = d i und f i sein; a d f und i d f sind in Wirklichkeit 2 einander gleiche Dreiecke, o i muss daher = k o sein. Oder kann zu demselben Zweck die senkrechte Mittellinie eines Giebelfeldes z. B. m f benüzt werden: f p wird = m f gemacht und eine mit a b parallele Linie von p nach der senkrechten Mittellinie des ganzen Turmes gezogen.

§ 59. Soll ein viereckiges Türmchen an beliebiger Stelle auf ein Giebeldach gesezt werden, wie in Fig. 57, so geht die Construction am besten von der mit a b parallelen Linie c d aus, deren Länge nach Gutdünken bestimmt wird. Man errichtet über c und d 2 Senkrechte, bildet mit denselben ein Rechteck m n o p und zieht aus n durch den Halbierungspunkt von m o eine Linie, welche in f die verlängerte o p trifft und damit die Breite der ganzen Seite angibt. Für die perspectivische Breite der anstossenden Seite p g e c sind, wenn sie[77] genau berechnet werden soll, die im folgenden Abschnitt enthaltenen Regeln über die Construction des Quadrats massgebend.

In Fig. 58 ist ein ähnliches Türmchen auf die Mitte eines Giebeldaches gesezt. Ist wie hier die Grundfläche ein Quadrat, d. h. a b = b c, so ist wie bei Fig. 46 zu verfahren, nachdem von i, der Mitte der Firstlinie, die Linien i a, i b und i c gezogen[78] sind. Ist a b länger als b c oder umgekehrt, so schneide man von der Mitte der Firstlinie aus 2 perspectivisch gleich grosse Teile i d und i e entsprechend der gewünschten Grösse des oberen Türmchens ab, ziehe von d und e 2 schräge Linien parallel mit den Seitenlinien des Dachs abwärts und verfahre wie bei Fig. 57.

In Fig. 59 ist zuerst der Turmaufsaz über a b g h wie oben mittels der Linien d a, d b und d c construiert (vergl. Fig. 55, 56 und 57), die Punkte f und e ergeben sich sodann durch die senkrechten Mittellinien der beiden Seiten des Turmaufsazes.

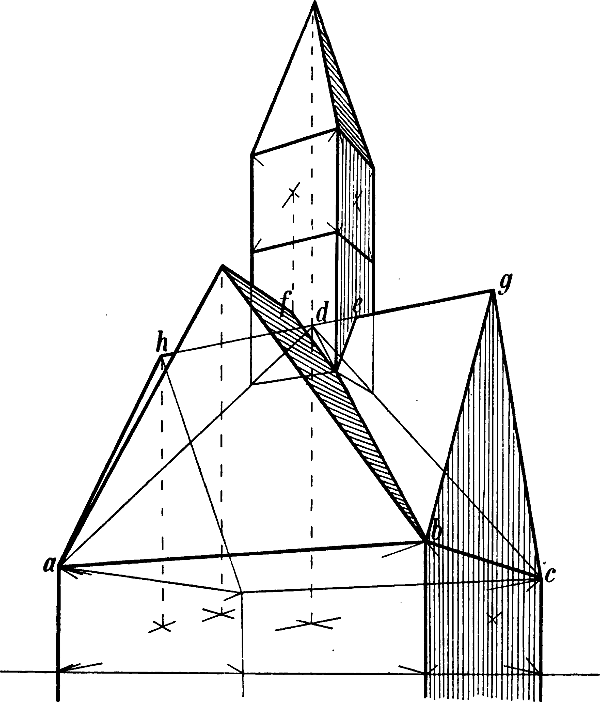
§ 60. Fig. 60 ist zuerst geradlinig wie Fig. 47 construiert, wodurch die für die perspectivische Schweifung der Ecklinien wichtigen Punkte n, m und k gewonnen werden.

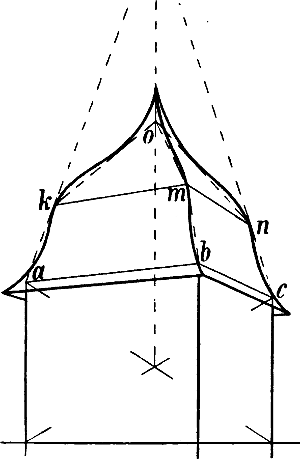
In Fig. 61 ist zuerst a b c d gezeichnet, sodann (vergl. Fig. 45) die Lage der Punkte k m n bestimmt, von welchen die[79] geschweiften Linien ausgehen, ferner die Lage der 3 Punkte, an welchen sie ihre stärkste Ausladung haben. Diese Punkte liegen ebenso wie k m n in 2 mit a b und b c parallelen Linien und ergeben sich, je nachdem die Ausladung eine stärkere oder schwächere ist, durch Verlängerung der senkrechten Ecklinien, wie x y z oder dadurch, dass von andern in gleicher Höhe liegenden Punkten der Linien a d, b d, c d, oder ihrer Verlängerung, z. B. von e, f und g, 3 Senkrechte und zwischen diesen in entsprechender Höhe 2 mit a b und b c parallele Wagrechte wie o h und o i gezogen werden.

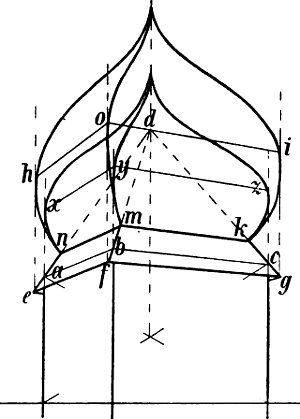
§ 61. In Fig. 62 ist schliesslich gezeigt, wie auf Grund der bisher angewandten Constructionslinien vorspringende Dächer zu zeichnen sind.

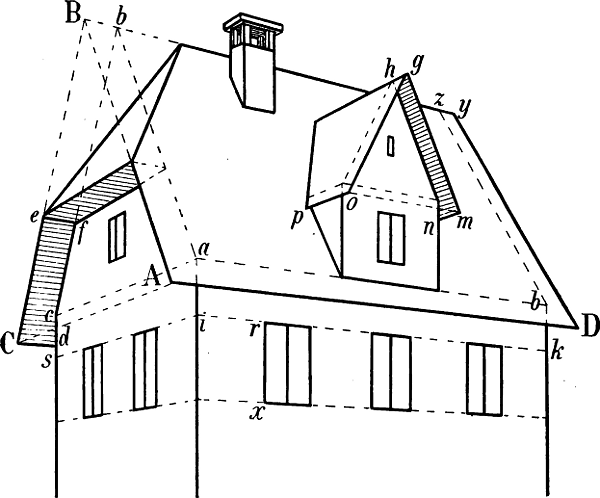
Nachdem A als vordere Ecke des Daches angenommen wurde, sind die mit a b, b c, a c und a t6 parallelen Linien A B, B C, A C und A D gezeichnet. C d und e f sind parallel mit A D, m n und o p mit A C. z y ist geometrisch = B b, aber entfernter, muss also entsprechend kleiner sein als B b. Selbstverständlich wird die Mitte der Giebelseiten bezeichnet durch die von b und h abwärts gezogenen Senkrechten und dürfen hiezu nicht die Punkte B und g benüzt werden.

IV. Die perspectivischen Grössenverhältnisse.

Unterscheidung der verschiedenen Aufgaben.

§ 62. Wir sind in § 22 ausgegangen von dem wichtigsten Gesez in Betreff der perspectivischen Grössenverhältnisse, wonach jeder Gegenstand im Verhältnis seiner Entfernung vom Auge kleiner zu werden scheint. Ferner wissen wir aus § 8, dass wir es nur mit der perspectivischen Grösse solcher Linien zu thun haben, deren geometrisches Grössenverhältnis zu andern Linien ein symmetrisches, regelmässiges und notwendiges ist.

Es lassen sich in dieser Beziehung 3 Fälle unterscheiden: 1) Parallellinien, welche in Wirklichkeit gleich lang sind, aber verschiedene Entfernung vom Auge haben (in verschiedener Tiefe sich befinden), wie z. B. in Fig. 62 die senkrechten Umrisslinien der 3 grösseren Fenster. 2) Verkürzte Linien, auf welchen sich gleich grosse Masse wiederholen, oder welche nach bestimmten symmetrischen Verhältnissen geteilt sind, wie die Linie i k Fig. 62, wenn die Fenster in Wirklichkeit gleiche Breite und gleiche Abstände haben. 3) Verkürzte Linien, welche zu einer nicht parallelen Linie in einem bestimmten Grössenverhältnisse stehen, wie die Seiten eines verkürzten Quadrats oder die Teile der Linie i s Fig. 62, wenn die Fenster und Zwischenräume in Wirklichkeit auf beiden Seiten gleiche Breite haben.

Parallellinien von gleicher Länge in verschiedener Tiefe.

§ 63. Die Berechnung der perspectivischen Länge paralleler Linien, welche geometrisch gleich gross sind, aber in ungleicher Tiefe liegen, geschieht nach dem § 1 angeführten Geseze, dass parallele Linien, welche zwischen 2 gleichfalls parallelen Linien liegen, gleich lang sind.

Mehrfache Beispiele sind schon in den vorangegangenen Figuren enthalten, z. B. in Fig. 20 sind i k und c d, g h und a b perspectivisch gleich lang (stellen Linien dar, welche geometrisch gleich lang sind), weil sie als unverkürzte Wagrechte unter sich parallel sind und die Linien a P und b P, c P und d P, zwischen welchen sie liegen, gleichfalls perspectivisch parallel sind, vergl. die gleich langen Linien a i, b g, k e und f h, oder a e und c d in Fig. 36, ähnliche Linien in Fig. 40 und 41 und andere. Soll in Fig. 62 die Linie r x massgebend sein für die Höhe der übrigen Fenster, so werden durch r und x 2 Linien parallel mit den wagrechten Linien dieser Seite bis zu der senkrechten Ecklinie gezogen und von lezterer aus auf der andern Seite parallel mit a c fortgesezt, wodurch sämtliche zwischen diesen Parallelen liegende senkrechte perspectivisch gleich lang sind.

§ 64. In Fig. 63 sei die Aufgabe gestellt, die Höhe der Figur a b auf die in derselben wagrechten Fläche liegenden Punkte c, e und g zu übertragen oder auf den leztgenannten Punkten Figuren von gleicher Höhe mit a b zu zeichnen. Ziehen wir von a durch c eine Linie nach dem Horizont, und nach dem Punkte x, wo sie denselben trifft, eine zweite von b aus, so sind alle senkrechten Linien, welche zwischen den 2 Parallellinien a x und b x liegen, perspectivisch gleich hoch. Eine Linie von a durch e oder von g durch a nach dem Horizont[83] würde diesen in 2 weit ausserhalb der Zeichenfläche liegenden Punkten treffen. Man benüzt daher 2 von a und b nach einem beliebigen Punkt des Horizonts gezogene Linien, z. B. a x und b x, zieht von e eine unverkürzte Wagrechte nach i und errichtet dort die Senkrechte i k, welche somit in gleicher Tiefe mit e steht und mittels einer unverkürzten Wagrechten von k aus auf die gewünschte Stelle übertragen werden kann. Da eine von g aus nach der verlängerten x a gezogene Wagrechte die leztere nicht mehr innerhalb der Zeichenfläche erreichen würde, so ist ein Punkt y wie oben benüzt, von g eine Wagrechte[84] nach der verlängerten y a, d. h. nach m gezogen, m n = a b gemacht und ist somit auch g h = a b.

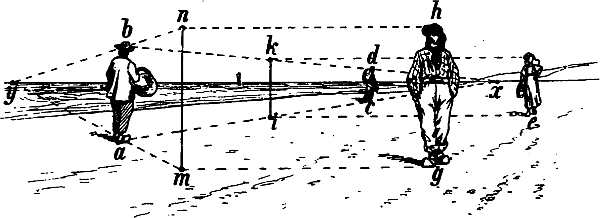
Liegt der Horizont in gleicher Höhe mit dem oberen Ende einer senkrechten Linie, z. B. in der Scheitelhöhe einer menschlichen Figur, so ist die Höhe aller gleich grossen senkrechten Linien oder anderer Figuren, welche in derselben wagrechten Fläche stehen, durch die Horizontlinie gegeben, vgl. Fig. 64.

§ 65. In Fig. 65 sei A B gegeben und sollen 2 weitere Figuren in f und g, d. h. in 2 Punkten gezeichnet werden, welche in gleicher Höhe und gleicher Tiefe mit den Punkten a und e liegen. Zu diesem Zweck sind die durch a und e gehenden Senkrechten verlängert bis zu der wagrechten Fläche, auf welcher A B steht, also bis o und p, und ist auf die oben beschriebene Weise o c = A B gemacht. Die Höhe o c kann nun mit dem Zirkel nach a d und von hier mittels einer Wagrechten nach f k übertragen werden. e p ist = o c = e b, somit ist auch g h = A B.

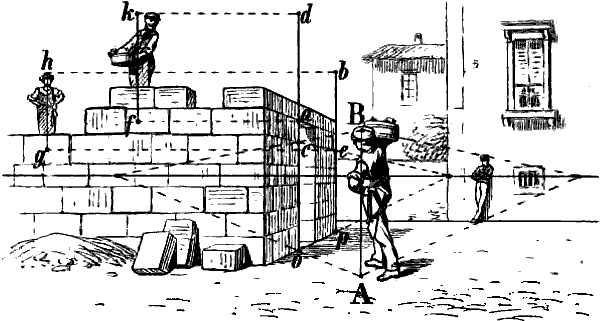
§ 66. In Fig. 66 ist angenommen, dass A B als Höhe einer in A stehenden Figur gegeben sei und der Punkt C, in[86] welchem eine zweite Figur stehen soll, um 3 Stufen tiefer liege, als die obere Fläche. Man errichte eine Senkrechte in g, mache i g = 3 mal g e, d. h. = a g, und i p = a b, d. h. = A B, ziehe i P und p P, eine Wagrechte von C nach m und errichte eine Senkrechte in m bis p P, so ist m n und folglich auch C D = A B.

Wäre die Höhe A B auf eine der beiden andern Stufen oder auf irgend einen Punkt der Fläche, in welcher g liegt, zu übertragen, so würde man bei b d, d f und f h = g e, e c und c a machen, so dass g h, e f und c d je = a b = A B wären und könnte hierauf jede dieser Senkrechten auf einen beliebigen Punkt der Fläche, in welcher ihr unteres Ende liegen soll, wie oben übertragen werden.

§ 67. In Fig. 67 ist die mit a b gleiche Höhe einer in c stehenden Figur berechnet, indem von c abwärts eine mit d f und g h parallele schräge Linie bis i, d. h. bis zu der wagrechten Ebene, in welcher a liegt, gezogen, die Höhe a b nach i k und hierauf mittels der weiteren schrägen Parallellinien k e nach c übertragen wurde. In einem derartigen Falle ist vorauszusezen, dass der Fluchtpunkt oder das Massdreieck einer in der betreffenden schrägen Fläche liegenden schrägen Linie, wie hier g m h, bekannt sei. Ein ähnliches Beispiel zeigt Fig. 35: Die Höhe g i ist zuerst mittels g n und i n nach f übertragen, wo die wagrechte Fläche beginnt, in welcher eine zweite Figur stehen soll. Die Höhe der lezteren ergibt sich sodann durch f P und e P.

Die perspectivische Grösse von Figuren oder irgend welchen Linien, welche auf unregelmässigem Terrain in verschiedener Tiefe sich wiederholen, kann nicht genau berechnet werden.

§ 68. Wie auf dieselbe oder ähnliche Weise wagrechte Parallellinien von gleicher Länge in verschiedener Tiefe zu zeichnen sind, ist in Fig. 68–70 gezeigt.

Es sei die Aufgabe gestellt, 2 Rechtecke von gleicher Grösse und in gleicher Stellung wie A B C D, Fig. 68, zu[87] zeichnen, so, dass die linke vordere Ecke des einen in E, die des andern in e liegt. Zieht man von E eine unverkürzte Wagrechte nach r, so ist r s = A B und kann mit dem Zirkel von E nach F übertragen werden. Die Richtung der verkürzten Seiten ist durch P gegeben, ihre Länge durch eine Linie von E nach z, dem Fluchtpunkt der Diagonale A C und folglich auch der mit A C parallelen E G. Ebenso kann e f = a b gemacht und die Länge f g durch die Diagonale e g bestimmt werden.

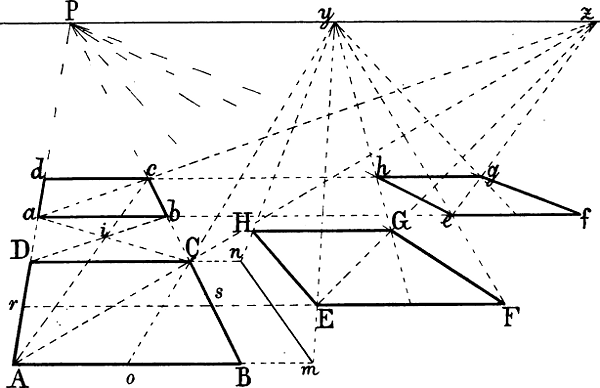
Wären die Fluchtpunkte beider Diagonalen des gegebenen Rechtecks A B C D unzugänglich, so könnten A B, E F und e f halbiert werden, um y als Fluchtpunkt von o C wie oben z behufs Berechnung der Länge F G und f g zu benüzen. e h könnte auch = F G gemacht werden mittels einer von F durch e nach dem Horizont und einer zweiten von G nach y gezogenen Linie. Sollte auf diesem Wege die Länge E H = B C bestimmt werden, so müsste, da eine Linie von B durch E[88] den Horizont ausserhalb der Zeichnung trifft, eine näher bei E liegende Linie, z. B. m n = B C gezeichnet werden, um m E y und n H y ziehen zu können.

§ 69. In Fig. 69 ist von a aus ein Rechteck = E F G H gezeichnet, indem von E eine Linie durch a nach dem Horizont gezogen und hierauf die Lage von b, c und d durch die Linien F P, G P, H P und die nach den betreffenden Fluchtpunkten gezogenen a b, b c, a d bestimmt wurde. Wäre statt a der Punkt A als vordere Ecke des zweiten Rechtecks gegeben, welcher in gleicher Tiefe mit E liegt, so könnte man von E, F, G und H unverkürzte Wagrechte nach links ziehen, in welchen auch die Punkte B, C und D liegen müssen und hierauf die Lage der lezteren ohne Hilfe ihrer Fluchtpunkte dadurch näher bestimmen, dass man nach einem beliebigen[89] Punkt des Horizonts, z. B. nach P, Linien von E, F, G, H und A zieht, und hierauf f g = i k, f C = i G, f e = i h macht u. s. w. Ebenso ist m n = x y, n o = y a u. s. w.

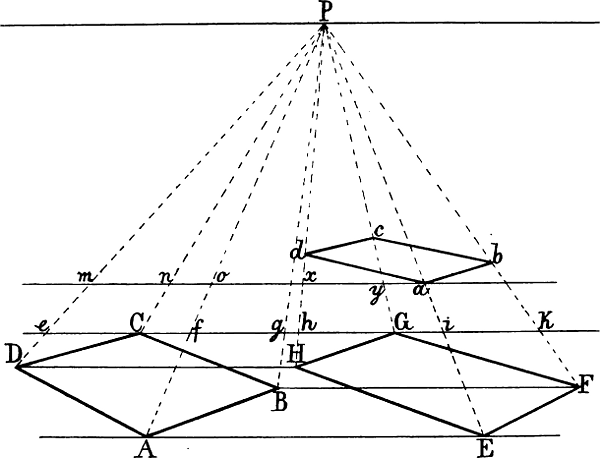
Wäre A B C D und der Punkt a gegeben, somit der Fluchtpunkt einer von A durch a gezogenen Linie unzugänglich, so könnte auf die zulezt angegebene Weise das erstere Rechteck leicht soweit als nötig zur Seite gerückt werden, wie oben die Linie B C, Fig. 68 nach m n.

§ 70. Aus dem Vorangegangenen ergibt sich ein weiteres in vielen Fällen bequemes Mittel, die Richtung verkürzter Parallellinien, deren Fluchtpunkt unzugänglich ist, zu berechnen. Wenn in Fig. 70 E die vordere Ecke eines Rechtecks = A B C D sein soll und wie oben eine Wagrechte durch A sowie die Linien A E z, B z, C z und D z gezogen sind, so bilde man mit einer aus einem beliebigen Punkt des Horizonts z. B. aus[90] y durch B gezogenen Linie ein Dreieck a c B und ziehe c z. b d ist nun = a c, eine Linie von d nach y macht b F = a B, somit sind die Dreiecke a c B und b d F oder A a B und E b F einander gleich und ist E F perspectivisch gleich gross und parallel mit A B. Die Lage der Ecke G ist durch C z und die Diagonale E y gegeben, könnte aber gleichfalls dadurch berechnet werden, dass auf die angegebene Weise F h g = B f e gemacht und eine unverkürzte Wagrechte von h nach G gezogen würde. Um K zu erhalten, ist schliesslich D m gezogen, durch m z G n = C m gemacht, und durch eine Wagrechte von n nach D z der Punkt K bestimmt.

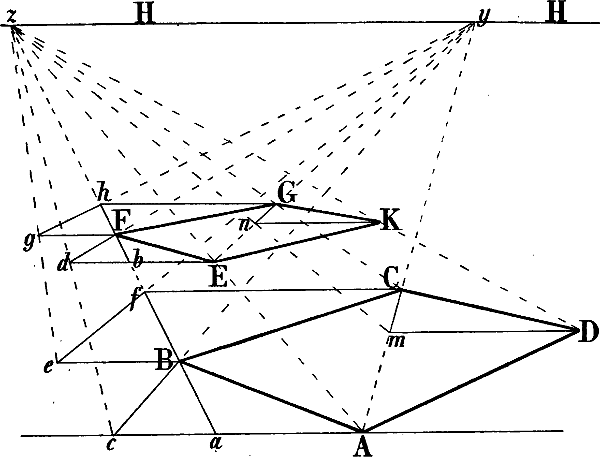
Da sowohl Richtung als Länge einer schrägen Linie durch die senkrechte und wagrechte Linie ihres Massdreiecks gegeben ist, so gilt das Gesagte auch für verkürzte gleich grosse schräge Parallellinien in verschiedener Tiefe.

Teilung einer verkürzten Linie nach bestimmten Verhältnissen.

§ 71. Die einfachste und häufigste Art einer solchen Teilung ist die Halbierung mittels der Diagonalen eines Rechtecks, dessen eine Seite die zu halbierende Linie bildet. Die vorangehenden Figuren, z. B. 38–41, bieten hievon mehrfache Beispiele. Ebenso von der Verdopplung einer Linie: in Fig. 48 z. B. ist, nachdem E h gegeben, die zweite Hälfte h F = E h gemacht mittels eines Rechtecks E h e c und einer Linie aus c durch die Mitte von e h nach F.

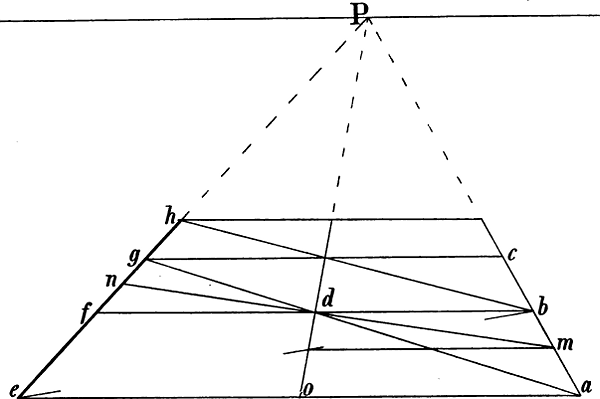
Soll in Fig. 71 die Länge e f auf der Fortsezung dieser Linie wiederholt werden, so bilde man mit e f ein beliebiges Rechteck e f b a, ziehe von a eine Linie durch die Mitte von b f nach g, von b durch die Mitte von c g nach h u. s. w. Auf dieselbe Weise ist in Fig. 72 die Länge a b nach c u. s. w. übertragen. In Fig. 71 ergibt sich f n als Hälfte von e f, wenn m[91] (vom Schnittpunkt der Diagonalen a f und e b aus) als Hälfte von a b bestimmt und von da eine Linie durch d gezogen wird.

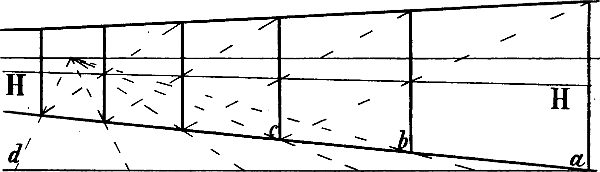
In der Mitte des Rechtecks a b c d Fig. 73 kann ein Fenster gezeichnet werden, indem die senkrechte Mittellinie e f gezogen, m n o p als nähere Hälfte angenommen und n z durch die Mitte von m p gezogen wird, vgl. die beigefügte geometrische Figur.

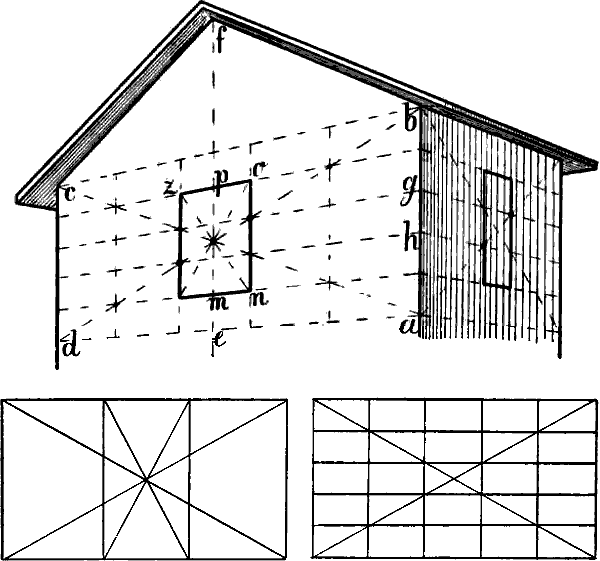
Soll auf der Linie B P Fig. 68 von b aus ein Stück = B C abgeschnitten werden, so bilde man ein Rechteck C b a D, ziehe D b und C a und durch i eine Linie von A nach c.

§ 72. Die Teilung einer verkürzten Linie in eine grössere Anzahl von Teilen, welche in einem bestimmten geometrischen Verhältnis zu einander stehen, geschieht gewöhnlich zufolge dem Geseze, dass in einem Dreieck Linien, welche parallel mit einer Seite zwischen den beiden andern gezogen werden, auf lezteren Teile von gleichem Verhältnis ergeben.

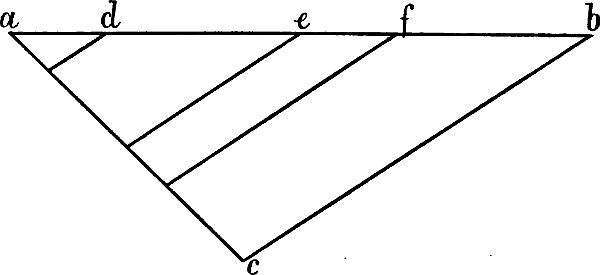
In Fig. 74 ist z. B. die Linie a b so geteilt, dass a d und e f gleich gross und je die Hälfte von d e und f b sind. Zieht man nun von f, e und d Linien parallel mit b c nach a c, so[93] erhält man auf lezterer Linie Teile von demselben Verhältnis. Ist die Aufgabe gestellt, die Linie D C Fig. 75 so zu teilen, dass die Fenster je halb so gross als die Zwischenräume sein sollen, so wird durch D eine unverkürzte Wagrechte gezogen, mit dem Zirkel, nachdem D a als erster Teil beliebig angenommen ist, a b = 2 mal D a, b c = D a u. s. w. gemacht und eine Linie von f, dem Endpunkt des letzten Teilabschnitts, durch C nach dem Horizont gezogen, worauf die Linien a p, b p, c p u. s. w. auf D C die gewünschten Verhältnisse ergeben.

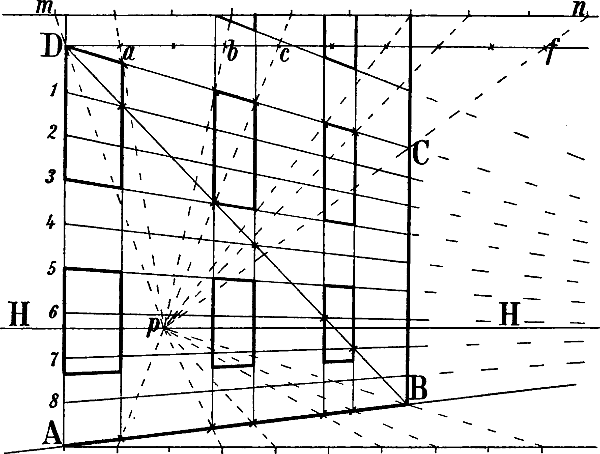
Statt auf D f könnten die Teile auch auf einer höher gelegenen Linie, z. B. von m aus in der Weise angetragen werden, dass eine Linie von m durch D nach dem Horizont, eine zweite von p durch C nach n gezogen und m n mit dem Zirkel nach den gewünschten Verhältnissen geteilt würde.

Auch in Fig. 72 könnte auf diese Weise die perspectivische Weite der Zwischenräume berechnet werden, wie auf der Linie a d angedeutet ist.

Dasselbe Verfahren ist in Fig. 42 angewandt, um die verkürzte schräge Linie b d in eine Anzahl gleicher Teile zu teilen und so die perspectivische Höhe der Stufen zu bemessen, mit dem Unterschied, dass die senkrechte Linie b e hier die Stelle der unverkürzten Wagrechten in Fig. 75 vertritt.

§ 73. Ein anderes Verfahren ist das folgende: Wenn in Fig. 73 das Rechteck a b c d gegeben ist und die Breite eines in der Mitte davon zu zeichnenden Fensters ⅕ der Linie a d betragen soll, so wird a b in 5 gleiche Teile geteilt und die Diagonale a c oder b d gezogen. Zieht man nun von g und h Linien parallel mit a d und b c, so erhält man da, wo dieselben die Diagonalen schneiden, die Punkte, welche die Breite des Fensters bestimmen, vergl. die geometrische Figur. Auch die perspectivische Breite der Fenster und der Zwischenräume in Fig. 75 könnte dadurch bestimmt werden, dass A D mit dem Zirkel in 9 gleiche Teile geteilt würde (vorausgesezt, dass das oben angegebene Verhältnis massgebend sein soll). Die Punkte, in welchen die von 1, 3, 4, 6 und 7 aus gezogenen Parallelen die Diagonale D B schneiden, ergeben, wie die Figur zeigt, dasselbe Verhältnis wie die obige Berechnung.

Perspectivisches Grössenverhältnis nicht paralleler Linien.

§ 74. Wenn wir uns von unserem Auge eine Linie nach dem Augpunkt und 2 andere nach den beiden Diagonalpunkten (§ 18) gezogen denken, so entstehen 2 gleichschenklige rechtwinklige Dreiecke. Denn eine Linie vom Auge nach dem Augpunkt steht zum Horizont in einem rechten Winkel und die Entfernung der Diagonalpunkte vom Augpunkt ist gleich der Entfernung des Auges vom Augpunkt. Wenn in Fig. 76 D unser Auge, P der Augpunkt ist, so sind Dp und Dg Diagonalpunkte.

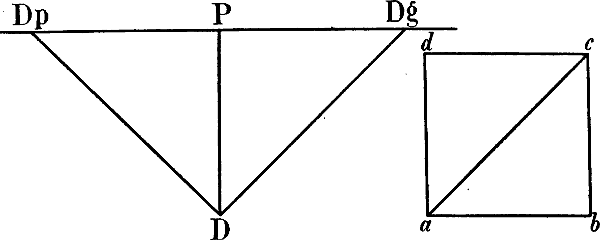
Die beiden Linien vom Auge nach den Diagonalpunkten – D Dp und D Dg – stehen zum Horizont in einem halben rechten Winkel, wie die Diagonalen eines Quadrats zu dessen Seiten, vergl. a b c d. Steht eine Linie unseres Gegenstands in einem halben rechten Winkel zu einer unverkürzten Wagrechten, so steht sie auch zum Horizont in einem halben rechten Winkel, sie ist also parallel mit einer Linie von unserem Auge nach einem der beiden Diagonalpunkte und dieser muss ihr Fluchtpunkt sein. Die Diagonalpunkte sind also die Fluchtpunkte aller wagrechten Linien, welche zu einer unverkürzten Wagrechten in einem halben rechten Winkel stehen.

Umgekehrt, jede Linie des Bildes, deren Fluchtpunkt ein Diagonalpunkt ist, stellt eine Linie dar, welche zum Horizont und zu den unverkürzten Wagrechten derselben Zeichnung in einem halben rechten Winkel steht.

Ist also in Fig. 77 die Distanz = 2 mal A P = P Dg, so ist Dg ein Diagonalpunkt und stellt A C eine Linie dar, welche in einem halben rechten Winkel zu A B steht; die Linie B C, welche ihren Fluchtpunkt im Augpunkt hat, ist[96] demnach eine rechtwinklig zu A B stehende Linie und A B C ist die perspectivische Form eines gleichschenkligen rechtwinkligen Dreiecks = a b c Fig. 76. B C Fig. 77 ist = A B, wie in Fig. 76 b c = a b ist.

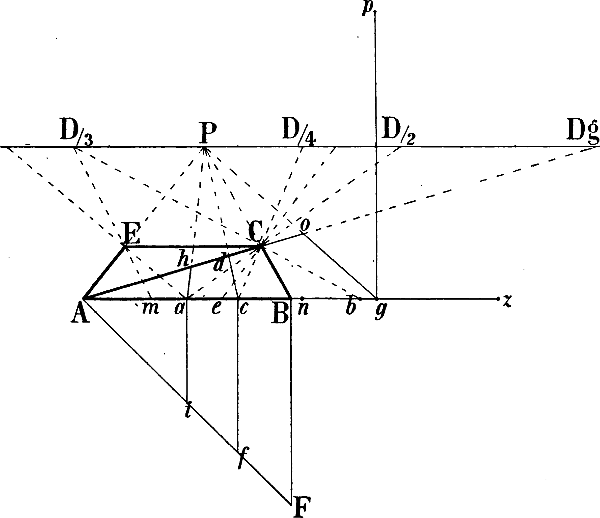
§ 75. Demgemäss kann die Länge einer unverkürzten Wagrechten auf eine rechtwinklig zu ihr stehende, d. h. nach dem Augpunkt gehende Wagrechte übertragen werden, indem entweder von einem Endpunkt der gegebenen unverkürzten[97] Wagrechten eine Linie nach einem der beiden Diagonalpunkte gezogen wird, welche die nach dem Augpunkt gehende Linie schneidet: B C Fig. 77 wird = A B gemacht durch eine Linie von A nach Dg, welche die Linie B P in C schneidet; oder indem man eine Linie von einem Diagonalpunkte durch einen Endpunkt der gegebenen unverkürzten nach der verkürzten Wagrechten zieht: so wird E A = C E mittels einer Linie von Dg durch C nach A. A B C E ist somit die perspectivische Form eines wagrecht liegenden Quadrats.

Ebenso kann die Länge einer nach dem Augpunkt gehenden Linie auf eine anstossende unverkürzte Wagrechte übertragen werden: durch Dg C A wird A B = B C, durch A C Dg wird C E = A E gemacht.

§ 76. Ist in Fig. 77 die Distanz = 2 mal P A, so ist D/₂ die Hälfte, D/₃ ein Drittel, D/₄ ein Viertel der Distanz. Ebenso ist B a die Hälfte, B b oder B e ein Drittel und B c ein Viertel von A B. Ziehen wir, statt von A nach Dg, eine Linie von a nach D/₂ oder von b nach D/₃ oder von c nach D/₄, so wird von der aus B nach P gehenden Linie dieselbe Länge B C abgeschnitten; gehen wir von der verkürzten Linie B C aus, so erhalten wir durch eine aus D/₂, D/₃ oder D/₄ durch C gezogene Linie auf der durch B gehenden Wagrechten die Hälfte, ein Drittel oder ein Viertel von B C.

Da ein Diagonalpunkt stets ausserhalb der Zeichnung liegt, so bedarf man eines Ersazmittels, welches durch jene Teilpunkte gegeben ist: soll B C = A B gemacht werden, so zieht man eine Linie von a nach D/₂, von b nach D/₃ oder von c nach D/₄, soll A B = B C gemacht werden, so erhält man durch eine Linie von D/₂ nach a, D/₃ nach b u. s. w. zunächst die Hälfte, ein Drittel oder Viertel von A B und kann hienach mit dem Zirkel die ganze Länge A B leicht ergänzt werden. Statt der Linie b D/₃ könnte auch eine Linie von e nach dem rechts vom Augpunkt liegenden Drittel der Distanz [98]gezogen werden, sowie man statt der rechtsseitigen Punkte D/₂ und D/₄ die entsprechenden Teilpunkte links vom Augpunkt benüzen und mittels derselben rechts von B die Hälfte oder ein Viertel von A B abschneiden könnte.

§ 77. Hienach ist es leicht, auch einer nach einem Distanzpunkt gehenden Linie jedes beliebige Grössenverhältnis zu einer anstossenden unverkürzten Wagrechten zu geben oder umgekehrt. Wird z. B. in Fig. 77 die Senkrechte B F = A B gemacht, so ist das Dreieck A B F = A B C (da auch B C = A B ist); A C ist = A F = A g; A f ist = A d = A n, A h = A i. Es kann also ein beliebiger Teil der Linie A z mit dem Zirkel auf A F oder ihre Verlängerung und von hier mittels einer Senkrechten und einer nach dem Augpunkt gehenden Linie auf die Linie A Dg übertragen werden.

Soll die Länge der nach einem Distanzpunkt gehenden Linie A C auf die durch A gezogene Wagrechte übertragen werden, so zieht man eine Linie von P durch C nach B, eine[99] Senkrechte B F = A B und macht mit dem Zirkel A g = A F = A C.

Das unverkürzte Dreieck kann natürlich ebensowohl oberhalb als unterhalb der Linie A B gebildet werden. Um z. B. A o auf A B zu übertragen, kann P o g gezogen, die Senkrechte g p = A g errichtet und A z = A p gemacht werden.

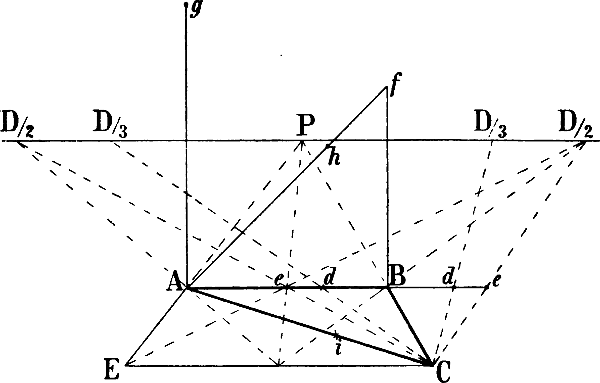
Oder sei in Fig. 78 A B die zuerst gegebene Linie, D/₂ die Hälfte, D/₃ ein Drittel der Distanz. B e ist die Hälfte, B d ein Drittel von A B; somit wird B C = A B mittels einer Linie von D/₂ durch e, oder von D/₃ durch d. B f ist = A B, also ist A B f = A B C; A f ist = A C; A h ist = A B, also erhält man auf A C den Teil A i = A B, indem man eine Senkrechte von h nach A B, und durch den Punkt, in welchem sie A B trifft, eine Linie von P aus zieht.

§ 78. Mit Hilfe desselben Verfahrens kann nun das perspectivische Grössenverhältnis jeder verkürzten wagrechten Linie zu einer andern bemessen werden. Nehmen wir an, dass in Fig. 79 D/₂ als Hälfte der Distanz, die perspectivische Richtung der (nicht nach einem Diagonalpunkt gehenden) Linien A B und A C, sowie die perspectivische Länge A B gegeben und die Aufgabe gestellt sei, leztere auf A C zu übertragen, so wird durch A eine unverkürzte Wagrechte und nach dieser aus dem Augpunkt eine Linie durch B gezogen. B b steht somit rechtwinklig zu A b; da D/₂ die Hälfte der Distanz ist, so ist b f = die Hälfte von B b; b c ist = 2 mal b f, also = B b, folglich ist A c = A B. Hierauf ist durch einen beliebigen Punkt o der zweiten Linie gleichfalls eine Linie aus P und aus D/₂ gezogen und hiedurch gefunden, dass o n = m n (= 2 mal n p) ist; A d wird nun = A c gemacht und schliesslich eine Senkrechte von d nach a und eine Linie von hier nach P gezogen, wodurch sich die Länge A C = A B ergibt.

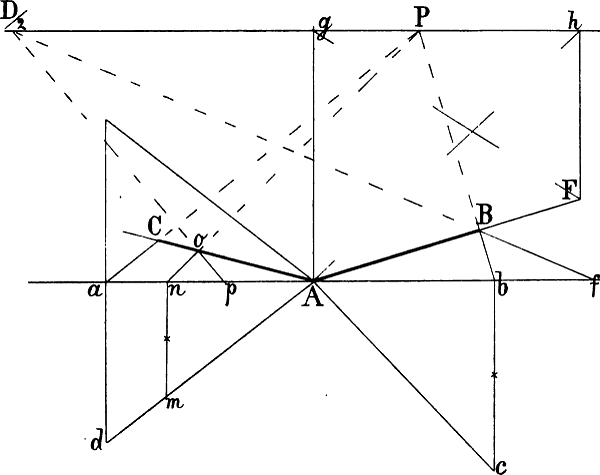
Wäre A F statt A B als Mass gegeben, so dass eine von D/₂ durch F gezogene Linie die durch A gehende Wagrechte nicht mehr innerhalb der Zeichenfläche treffen würde, so können[100] 2 Senkrechte A g und F h bis zum Horizont und die Diagonalen F g und A h gezogen und kann von ihrem Schnittpunkt aus durch eine Senkrechte der perspectivische Halbierungspunkt von A F gefunden werden, um auf dem angegebenen Wege zunächst die Hälfte von A F auf die Linie A a zu bringen. Ist angenommen, dass die beiden verkürzten Linien einen rechten Winkel darstellen, so wird auf kürzerem Wege A C = A B gemacht, indem mit dem Winkel (Fig. 9) A d = A c rechtwinklig zu A c gezeichnet und hierauf d a und a P gezogen wird.

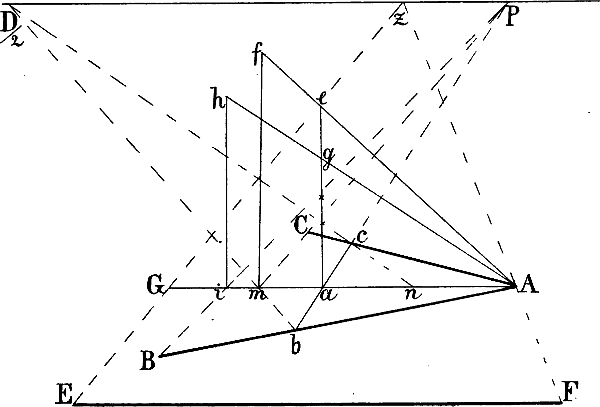
In Fig. 80 sind die Wagrechten A B und A C, deren Richtung von A aus gegeben ist, = der in gleicher Fläche liegenden E F gemacht. Zu diesem Zweck ist zunächst A G = E F gemacht mittels einer Linie von F durch A nach z und einer zweiten von z nach E und ist hierauf von P eine[101] Linie nach einem beliebigen Punkte b der Linie A B gezogen. D/₂ sei die Hälfte der Distanz; also ist a c = 2 mal a n, a b = 2 mal a m, das wagrechte Dreieck A a c ist somit = dem senkrechten A a e, A a b ist = A a g (a e = 2 mal a n, a g = 2 mal a m). Nachdem nun A f und A h = A G gemacht sind, werden die Senkrechten f m und h i gezogen und ergeben die von P nach m und durch i nach B gezogenen Linien die Länge A C und A B = A G = E F.

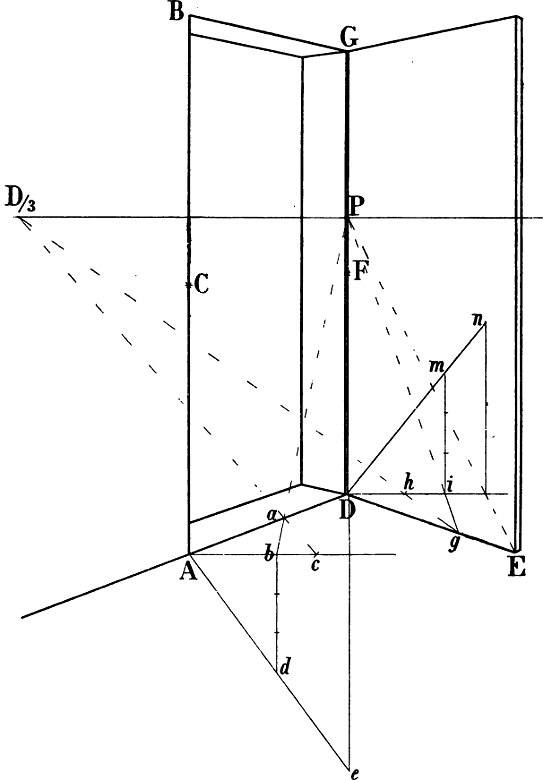
Fig. 81 zeigt die Anwendung des Vorangegangenen auf eine geöffnete Thüre. Es ist angenommen, dass die Länge A B und die Richtung A D gegeben, die Richtung D E beliebig und die Breite der Thüre = A C sein soll. In beliebiger Richtung ist aus P nach der durch A gehenden Wagrechten die Linie a b gezogen, welche, wenn D/₃ ein Drittel der Distanz darstellt, = 3 mal b c, also = b d ist; A e ist = A C, somit ist auch A D = A C. Nun ist eine Wagrechte durch D gezogen[103] und in gleicher Weise zuerst an beliebiger Stelle ein Dreieck D m i = D g i construiert (i m = 3 mal i h), um sodann D n = D F, D E = D n zu machen; D F ist = A C, somit ist E D ebenfalls = A C.

§ 79. Kann die Länge einer verkürzten auf eine unverkürzte Wagrechte übertragen werden und umgekehrt, so ist damit auch das Mittel gegeben, eine bestimmte Grösse von einer Senkrechten oder einer unverkürzten schrägen Linie auf eine verkürzte Wagrechte zu übertragen und umgekehrt, vgl. Fig. 81, wo die Linien A D und E D = der Senkrechten A C gemacht wurden, oder Fig. 78, wo A C = der unverkürzten schrägen Linie A f und = der Senkrechten A g ist.

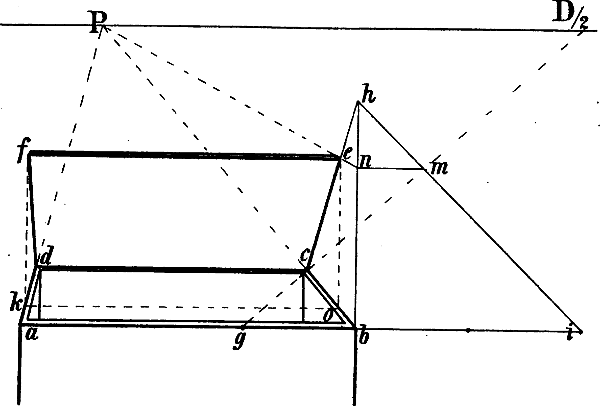
Die Berechnung der perspectivischen Länge einer verkürzten schrägen Linie ist in Fig. 82 und 83 gezeigt. In beiden Beispielen ist die Richtung der Linien c e und b c, sowie[104] die Länge b c als gegeben angenommen und soll c e = b c gemacht werden. Es ist zunächst die Länge b c auf die durch b gehende Wagrechte zu übertragen. In Fig. 82 geht b c nach dem Augpunkt, folglich ist b g die Hälfte von b c. Die von c ausgehende schräge Linie ist bis zu einer in b errichteten Senkrechten verlängert, b i ist = 2 mal b g, d. h. = b c, somit ist das Dreieck b i h = b h c; i m ist = b i = b c; zieht man eine unverkürzte Wagrechte von m nach n und von n eine mit b c parallele Linie nach P, so ist c e = i m = b c. Eine Senkrechte von e nach o, eine Wagrechte von o nach k und eine Senkrechte von k nach f ergeben f d als die mit c e parallele Seite.

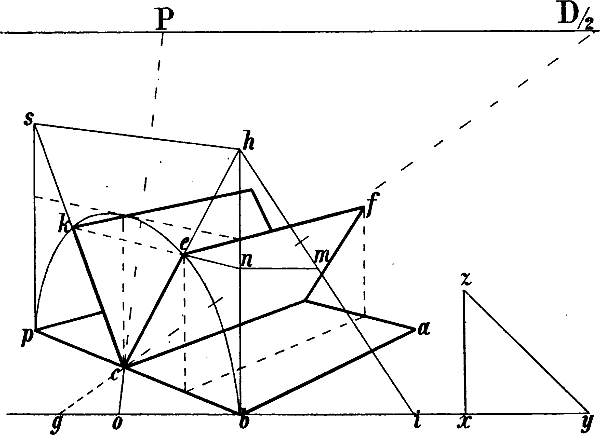
In Fig. 83 ist zuerst eine Linie von P durch c nach o gezogen; c o ist = 2 mal o g = x z, x y ist = o b; folglich ist das Dreieck b o c = x y z und b c ist = y z = b i, das Dreieck b i h ist = b h c u. s. w.

Ist statt c e die Richtung der Linie c k gegeben und soll auf leztere die Länge c b übertragen werden, so kann c p = c b gemacht (vgl. Fig. 68) und links von p s ein unverkürztes Dreieck = c p s gebildet werden; oder kann, wenn der Raum dies nicht gestattet, s h parallel mit b p gezogen, der Punkt n wie oben bestimmt und von hier aus mittels n k die schräge Linie c k = b c gemacht werden.

Eine andere Lösung der Aufgabe wäre die Construction eines Halbkreises über b p, indem alle von diesem nach c gezogenen Linien = b c sein würden.

Das Quadrat in gerader Stellung.

§ 80. Die perspectivische Form eines wagrecht liegenden Quadrats in gerader Stellung ist gegeben durch den Augpunkt, welcher die Richtung der beiden verkürzten Seiten bestimmt (§ 32) und durch die Diagonalpunkte, welche Fluchtpunkte der beiden Diagonalen sind und hiemit das perspectivische Grössenverhältnis der Seiten zu einander angeben (§ 74); die Ausführung ist aus § 74–75 und aus Fig. 77–78 ersichtlich.

Auch in diesem Fall kommt es hauptsächlich darauf an, dass die Entfernung des betreffenden Diagonalpunkts vom Auge, welche gleichbedeutend ist mit der Distanz, nicht zu klein angenommen werde (§ 34). Die Folge wäre, dass die verkürzten Seiten zu lang erscheinen würden im Verhältnis zu den unverkürzten. E F B D Fig. 84 kann ebensowohl ein Quadrat darstellen, als E F G H; der Unterschied ist nur, dass die leztere Form einen näheren Standpunkt voraussezt als die erstere. Sobald wir aber die Linie G H näher nach dem Horizont hin rücken, z. B. nach m n, so erscheinen die beiden verkürzten Seiten länger als die unverkürzten. Denn P D/₂ ist = P F und 2 mal P F ist in diesem Fall die kleinste Distanz, welche angenommen werden kann.

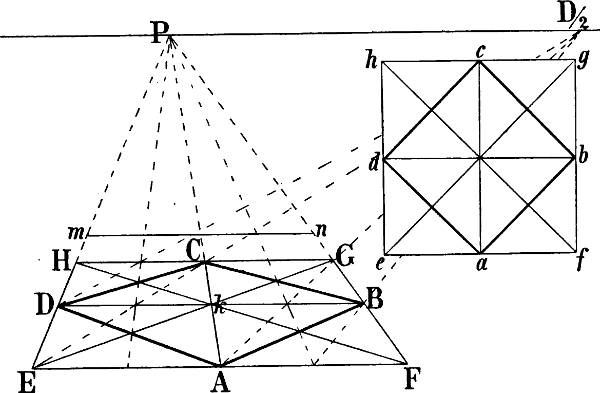
Es ist daher im allgemeinen darauf zu achten, dass bei der besprochenen Stellung des Quadrats der Punkt, in welchem eine Linie von der Mitte der unverkürzten Vorderseite durch eine gegenüberliegende Ecke nach dem Horizont (A G oder A H, Fig. 84) diesen trifft, wenigstens ebenso weit vom Augpunkt entfernt sein muss, als dieser von der entferntesten Ecke des Bildes.

Das Quadrat in schräger Stellung.

§ 81. Ist die Stellung des Quadrats eine solche, dass die eine Diagonale eine unverkürzte Wagrechte ist, so steht die andere rechtwinklig zum Horizont, hat also ihren Fluchtpunkt im Augpunkt und die Seiten haben dieselbe Stellung, welche im vorhergehenden Fall die Diagonalen hatten, ihre Fluchtpunkte sind die beiden Diagonalpunkte, s. Fig. 77. Ist A D in Fig. 84 als erste Seite eines solchen Quadrats gezeichnet,[107] also angenommen, dass der Fluchtpunkt von A D ein Diagonalpunkt sei, so ergibt sich B dadurch, dass eine unverkürzte Wagrechte von D nach rechts, eine Linie von A nach P gezogen und hierauf k B = D k gemacht wird, der Punkt C durch P D E, A E und eine Linie aus E durch die Mitte von D k nach A P. Oder man bildet das einschliessende Quadrat in gerader Stellung und bestimmt in diesem die Halbierungspunkte der Seiten.

§ 82. Wie die geometrisch gezeichneten Quadrate a b c d und e f g h, Fig. 84 zeigen, entstehen, wenn durch Verbindung der Halbierungspunkte a b c d ein kleineres Quadrat innerhalb des grösseren gebildet wird, zwischen beiden 4 gleichschenklige rechtwinklige Dreiecke von gleicher Grösse: a f b, b g c u. s. w. Wird eine Quadratseite in zwei ungleiche Teile geteilt und dieselbe Teilung auf den 3 andern Seiten wiederholt, wie in Fig. 85 (a f = b g = c h = d e und folglich a e = d h u. s. w.), so bilden die Verbindungslinien der 4 Teilungspunkte, hier a, b, c und d, gleichfalls ein Quadrat und entstehen wieder 4 rechtwinklige Dreiecke von gleicher Form und Grösse (a f b, b g c u. s. w.) mit dem Unterschiede, dass dieselben nicht gleichschenklig sind. Zieht man aus a und c 2 Linien parallel mit f g, aus d und b zwei weitere parallel mit e f je nach der gegenüberliegenden Seite des äusseren Quadrats, so ist e m = a f, m f ist = a e und dieselben Verhältnisse ergeben sich auf allen 4 Seiten.

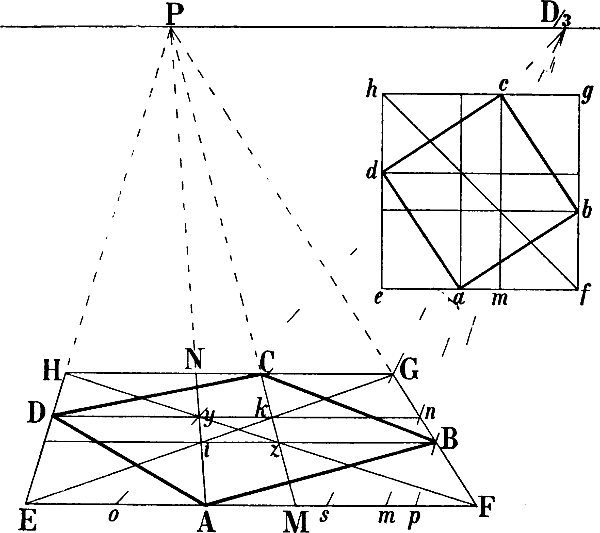
Ist nun ein verkürztes Quadrat in gerader Stellung z. B. E F G H Fig. 85, gegeben und in demselben ein Punkt A als vordere Ecke eines inneren Quadrats, dessen Ecken die Seiten des äusseren berühren sollen, so wird man F M = A E machen, M P und A P sowie eine Diagonale des äusseren Quadrats und durch die Schnittpunkte y und z oder i und k zwei Wagrechte ziehen, wodurch sich die Lage der Punkte B, D und C ergibt.

§ 83. Ist A B als Seite eines Quadrats und zweimal P F als Distanz angenommen, so zieht man eine Wagrechte durch A[108] und eine Linie aus P durch B nach F. Eine Linie aus D/₃ durch B ergibt F p als ein Drittel von B F, F M ist = 3 mal F p, also ist F M = B F. Wird nun A E = F M gemacht, so kann E P gezogen und das äussere Quadrat E F G H entweder durch Verlängerung der Diagonale des Quadrats M F B z oder durch eine Linie aus D/₃, nach s, d. h. dem Drittel von F E gebildet werden, worauf man wie oben verfährt.

Oder kann man, nachdem P F gezogen, F M = B F und A E = F M gemacht ist, E P und eine Linie von D/₃ nach m, d. h. einem Drittel von A F ziehen, wodurch das Quadrat A F n y entsteht. Die verlängerte n y ergibt den Punkt D, die verlängerte Diagonale F y den Punkt H, von wo aus eine Wagrechte die Linie M P in C schneidet.

Die Quadrate A F n y oder E M k D, durch welche der Punkt D gegeben ist, lassen sich auch ohne die zweite von D/₃ nach s gezogene Linie durch Verlängerung der Diagonale F z und die von A und M nach P gezogenen Linien bilden.

§ 84. Die Anwendung des hier beschriebenen Verfahrens kann überhaupt eine mannigfaltige sein. Wäre statt A B die Linie A D als erste Seite gegeben, so würde man mittels einer von D/₃ durch D gezogenen Linie auf der nach links verlängerten A E ein Drittel von A D erhalten oder zieht man eine Linie aus D/₃ durch y, wo sich A P und die von D nach rechts gehende Wagrechte schneiden, nach o, um A o oder E o als ein Drittel von E D zu bestimmen und somit E M = E D zu erhalten. Hierauf wird A F = E M gemacht und mit der verlängerten Diagonale des Quadrats E M k D, welche von F P in G geschnitten wird, das grössere Quadrat gebildet.

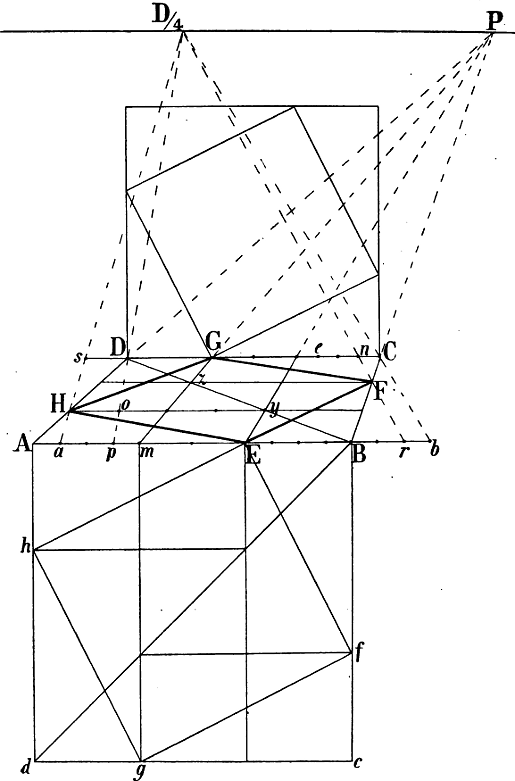
Fig. 86 zeigt dasselbe Verfahren mit etwas veränderter Stellung des inneren Quadrats. Die Distanz ist = 4 mal P A angenommen, also ist B r ein Viertel von B F; B m ist = 4 mal B r, also = B F, folglich ist das verkürzte Dreieck E B F = dem unverkürzten E B f. A H ist = 4 mal A a = A m und = A h, folglich ist A H E = A h E und man sieht deutlich, wie auch die übrigen Linien der zwei wagrechten Quadrate nach Grösse und Winkelstellung durch die Linien der senkrecht sich anschliessenden Quadrate A B c d und E f g h geometrisch wiedergegeben sind.

§ 85. Hiemit ist zugleich die genaue Berechnung der perspectivischen Form eines rechten Winkels in schräger Stellung gegeben, auf welche in § 33 verwiesen wurde.

Die Ausführung kann, wenn nur die 2 Linien des rechten Winkels verlangt sind, in wesentlich vereinfachter Weise stattfinden. Wenn z. B. in Fig. 86 von E aus eine zu E F rechtwinklige Linie gezeichnet werden soll, so genügt hiezu eine Linie von D/₄ durch F, wonach E A = 4 mal B r, d. h. = B F zu machen ist, eine zweite Linie von A nach P und eine[111] dritte von D/₄, nach a, indem A a ein Viertel von E B und somit A H = E B ist. Ist E H gegeben und soll eine rechtwinklig dazu stehende Linie gezeichnet werden, so bilde man das Rechteck H A E y, mache E B = A H (= 4 mal A a), ziehe B P und eine Linie von D/₄ nach r. Da B r ein Viertel von A E ist, so ist hiemit F B = A E. Welcher Weg im einzelnen Fall der bequemste, ob der Teildistanzpunkt links oder rechts vom Augpunkt für die Ausführung geeignet ist, wird man bei einiger Übung leicht erkennen.

Bei der Construction senkrecht stehender verkürzter Quadrate handelt es sich nur um die Übertragung eines gegebenen Masses von einer senkrechten auf eine verkürzte wagrechte Linie oder umgekehrt, worüber in § 74–78 das Nötige angegeben ist; ebenso ist aus § 78 zu ersehen, wie ein verkürztes schräges Quadrat zu zeichnen wäre; doch kommt die leztere Aufgabe seltener vor.

Vergrösserung oder Verkleinerung eines Quadrats oder Rechtecks.

§ 86. Wenn man in Fig. 87, nachdem g h i k gegeben ist, von b aus die mit g h und h i parallelen b f und b e zieht, oder wenn man 4 Punkte der Diagonalen g i und h k durch Linien verbindet, welche mit den Seiten parallel sind, so entsteht bei A wiederum ein Quadrat f b e k oder a b c d, bei B ein Rechteck f b e k oder a b c d, dessen Seitenpaare dasselbe Verhältnis von 2 : 3 haben, wie g h und h i. Wie auf die gleiche Weise aus einem kleineren ein grösseres Quadrat oder Rechteck durch Verlängerung der Diagonale gemacht werden kann, ist hienach leicht zu verstehen.

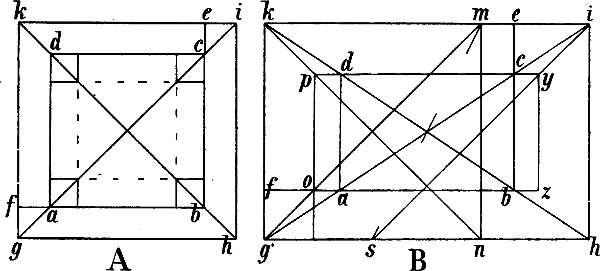
Aber während in A die Linien des inneren Quadrats a b c d überall gleich weit von g h i k entfernt sind, ist dies bei den Rechtecken a b c d und g h i k in B nicht der Fall: der Zwischenraum zwischen den kürzeren Seiten ist grösser, als zwischen[113] den längeren. Soll auf einem Wege, der auch bei verkürzter Stellung des Rechtecks anwendbar wäre, innerhalb g h i k ein (paralleles) Rechteck gezeichnet werden, so dass die Seiten beider überall gleiche Entfernung von einander haben, so muss auf einer längeren Seite z. B. auf g h ein Teil = der Länge der kürzeren Seite abgeschnitten, also z. B. g n = g k gemacht und so ein Quadrat g n m k gebildet werden, um dessen Diagonalen zu dem genannten Zwecke zu benüzen. Soll f g die Breite des Zwischenraums sein, so wird von f eine mit g h parallele Linie gezogen, welche die Diagonale g m in o schneidet und hiemit den Punkt p ergibt. Zieht man nun von m durch den Schnittpunkt der Diagonalen g i und h k eine Linie nach s, so ist g s = n h, s h = g n = h i; s i ist somit die Diagonale eines Quadrats = g n m k, und können die Punkte y und z durch die mit k i und i h parallelen Linien bestimmt werden.

§ 87. Die Construction der verkürzten Quadrate und Rechtecke in Fig. 88 und 89 ist hiemit gegeben. In Fig. 89 dient dieselbe dazu, die 4 Tischbeine an die richtige Stelle zu sezen. Fig. 90 stellt in grösserem Massstab die Verjüngung der Tischbeine nach unten dar.

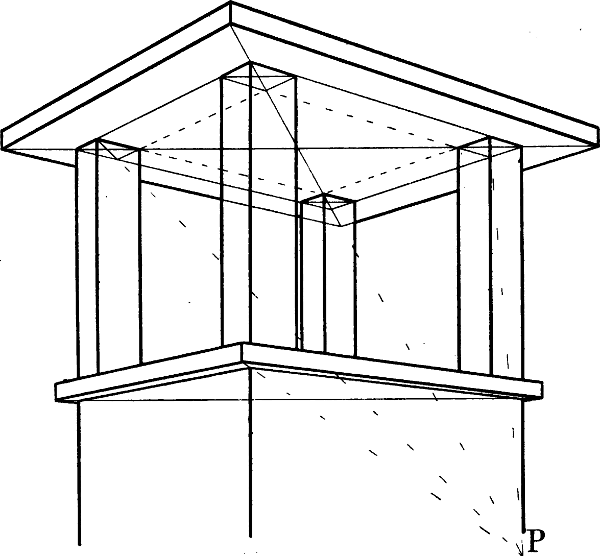
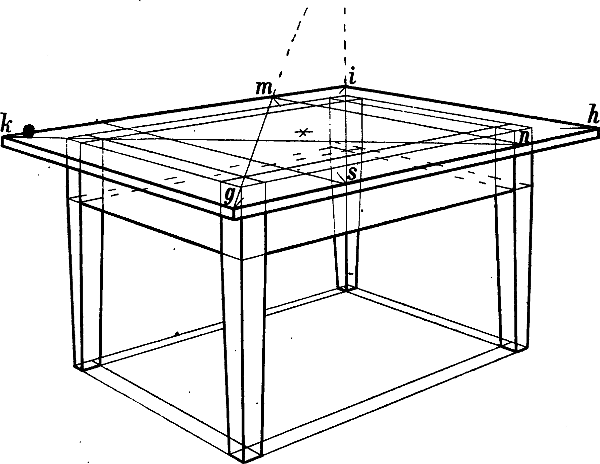
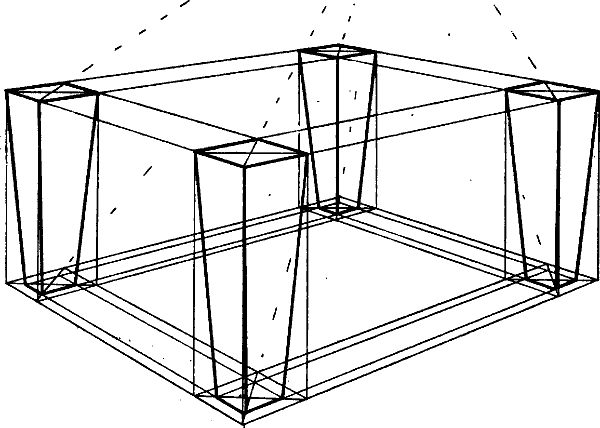
Fig. 91 zeigt einen Stuhl ohne Lehne. Der Siz bildet ein Quadrat, die Punkte a b c d, von welchen die Stuhlbeine ausgehen, ergeben sich daher durch die Diagonalen wie in Fig. 87 A und Fig. 88. Da sie nach auswärts stehen, so ist senkrecht unter a b c d das Quadrat e f g h gebildet und mittels seiner Diagonalen vergrössert.

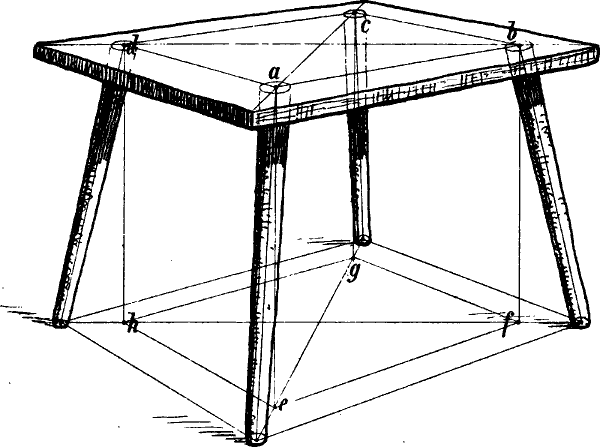
Stühle mit Lehnen sind gewöhnlich so geformt, dass der Siz hinten schmäler ist als vorn. Man kann deshalb, wenn beispielsweise a b Fig. 92 die Vorderseite des Sizes sein soll, zunächst ein Quadrat a b c d bilden, um sodann die Lage der geometrisch gleichweit von c und d entfernten Punkte e und f entweder auf früher beschriebene Weise oder nach dem Augenmass (e c kleiner als d f) zu bestimmen. Für die Punkte, von welchen die Füsse ausgehen, sind nun die Diagonalen a e und b f massgebend.

V. Verkürzte Kreise, Achtecke und Sechsecke. Gewölbeformen.

Der Kreis in verkürzter Stellung.

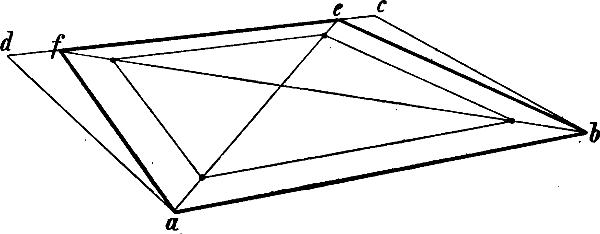
§ 88. Die Berechnung der perspectivischen Form eines verkürzten Kreises kann nur darin bestehen, dass gewisse Punkte desselben gewonnen werden, mit deren Hilfe es leichter ist, die Kreislinie aus freier Hand zu zeichnen. Die zu diesem Zweck geeignetsten Punkte sind die Halbierungspunkte der Seiten eines den Kreis einschliessenden Quadrats und ferner die Punkte der Diagonalen in lezterem, welche von der Kreislinie durchschnitten werden, vgl. die geometrische Zeichnung von Quadrat und Kreis in Fig. 93.

Gewöhnlich kann man sich eines Quadrats in gerader Ansicht bedienen. Die Halbierungspunkte der Seiten, a, b, c und d Fig. 93, erhält man mittels einer unverkürzten Wagrechten und einer nach dem Augpunkt gehenden Linie, welche durch den Schnittpunkt der Diagonalen gezogen werden. Ein geübter Zeichner wird sich für gewöhnlich mit diesen 4 Hilfspunkten begnügen können.

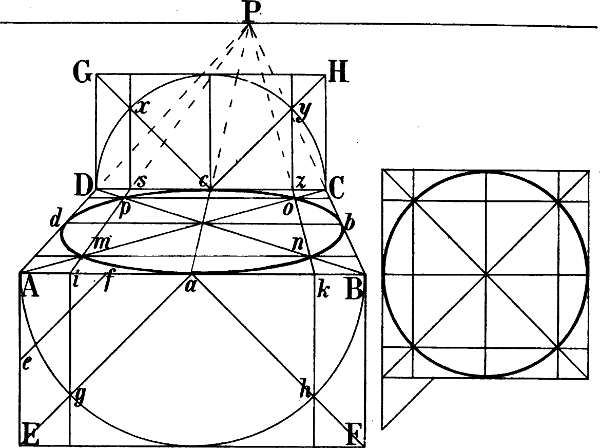
Um die Punkte der Diagonalen, welche der Kreis durchschneiden muss, m, n, o und p Fig. 93, zu erhalten, wird über oder unter einer der unverkürzten Seiten oder der unverkürzten Mittellinie, also mit A B, C D oder b d, ein senkrecht stehendes Rechteck halb so hoch als breit, z. B. A B F E oder C D G H gebildet und in diesem ein Halbkreis beschrieben. In Fig. 93[117] werden diese Halbkreise von den Diagonalen a E und a F oder c G und c H in g und h, y und x durchschnitten. Zieht man nun die Senkrechten g i und h k oder y z und x s und 2 Linien von P nach i und k oder durch s und z, so ergeben sich auf den Diagonalen des verkürzten Quadrats die gesuchten Punkte m, n, o und p. Es genügt auch nur eine der Linien nach dem Augpunkt zu ziehen, z. B. i P, um durch 2 unverkürzte Wagrechte von m und p aus die Punkte n und o zu erhalten.

§ 89. Ein anderes Verfahren beruht darauf, dass die Entfernung der Punkte i und k Fig. 93 von a, der Mitte der Linie A B, ebenso gross ist, als die Diagonale eines Quadrats, dessen Seiten je = ein Viertel von A B sind. A f ist ein Viertel von A B. Wird also A e = A f gemacht, so kann die Länge e f von a aus nach i und k übertragen und so die Lage dieser beiden Punkte und der Punkte m, n, o, p bestimmt werden.

§ 90. In Fig. 94 ist gezeigt, wie mittels derselben Hilfspunkte ein Kreis innerhalb eines Quadrats in schräger Ansicht gezeichnet werden kann. Nachdem in A B C D die Diagonalen und Halbierungslinien gezeichnet sind, ist eine Linie aus P durch B nach der durch A gehenden Wagrechten gezogen und A b ebenso geteilt, wie A B in Fig. 93. Statt abwärts von A aus ist hier seitwärts das Dreieck b g f gebildet, in welchem b g und g f je = ein Viertel von A b sind; a i und a k werden = b f gemacht und dieselben Verhältnisse mittels i P und k P auf die Linie A B übertragen.

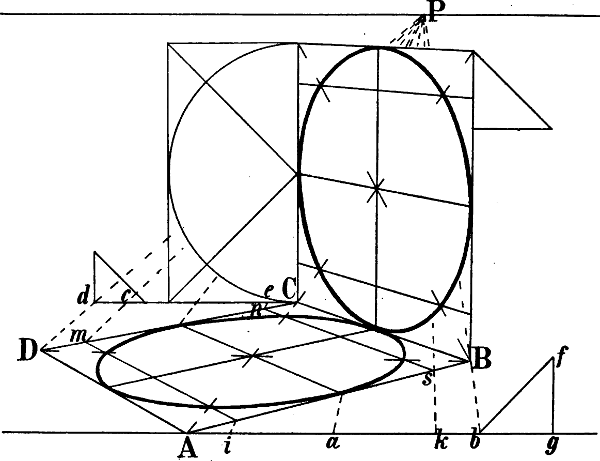
Aus § 72 Fig. 72 und 75 erhellt, dass man statt P auch einen beliebigen andern Punkt des Horizonts benüzen könnte, um von demselben eine Linie durch B nach der Linie A g zu ziehen und sodann wie oben weiter zu verfahren.

Statt durch A könnte man auch durch C eine Wagrechte und von D eine Linie nach P ziehen, um auf dieselbe Weise wie oben die Punkte e und c, m und n zu bestimmen.

Aus Fig. 94 ist zugleich die Anwendung der beiden in § 88 und 89 angegebenen Berechnungsweisen auf einen senkrecht stehenden Kreis zu ersehen. Es ist klar, dass hiebei die zwei senkrechten Seiten des Quadrats an Stelle der unverkürzten wagrechten treten und dass die Linien A E, B F, i g, h k der Fig. 93 jezt als Wagrechte gezeichnet werden müssen. Das Übrige ergibt sich deutlich genug aus den Linien der Fig. 94.

Parallele und concentrische Kreise.

§ 91. Fig. 95 zeigt 2 in gleicher Höhe stehende parallele Kreise. Der eine ist von dem Quadrat a b c d, der andere von e f g h umschlossen. Die Schnittpunkte der Diagonalen a c und b d, e g und f h ergeben die beiden Mittelpunkte y und z; die Punkte o, p, i, k sind auf die oben angegebene Weise bestimmt, die entsprechenden 4 Punkte auf e g und f h durch Linien, welche parallel mit a e und b f von k, o, p, i nach links gezogen sind.

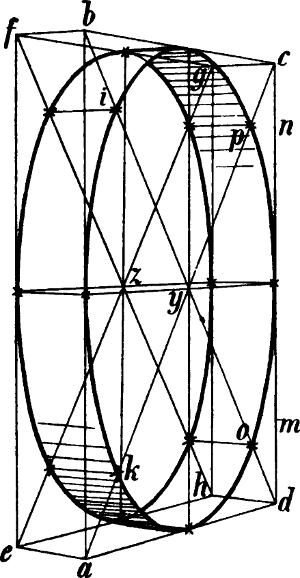
§ 92. In Fig. 96 soll, nachdem der Kreis A B C D gegeben ist, durch a ein Kreis mit dem gemeinschaftlichen Mittelpunkt i, sodann durch F ein mit A B C paralleler Halbkreis gezeichnet werden. Zunächst wird C c = A a gemacht, sodann das Quadrat des inneren Kreises gebildet, indem man durch a und c Linien nach dem Augpunkt zieht und die Punkte m und n, o und p, in welchen hiedurch die Diagonalen des grösseren Kreises geschnitten werden, durch 2 Wagrechte verbindet. Die Halbierungspunkte der Seiten dieses kleineren Quadrats sind a b c d. Die Punkte der Diagonalen, durch welche der innere Kreis geht, können auf die § 88–89 angegebene[120] Weise bestimmt werden, doch sind sie, wenn der Massstab der Zeichnung kein sehr grosser ist, entbehrlich, nachdem die Linie des äusseren Kreises gezeichnet ist.

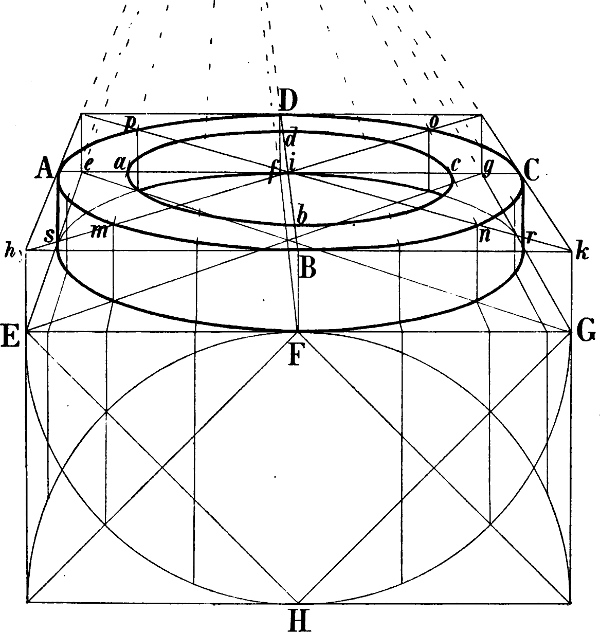
Um den unteren Halbkreis zu zeichnen, wird die durch F gehende E G mittels h E und k G = h k gemacht und das Quadrat E G g e gebildet, womit für den unteren Kreis ausser F die Punkte s, r und f gegeben sind. Die Punkte der Diagonalen E g und G e, welche er durchschneiden muss, ergeben sich durch die von m, n, o, p abwärts gezogenen Senkrechten.

Teilung eines verkürzten Kreises.

§ 92. In Fig. 96 ist zugleich gezeigt, wie diese Kreise in eine beliebige Zahl von gleich grossen Teilen geteilt werden können: mit dem Halbmesser F G ist von F oder von H aus[121] ein Halbkreis gebildet, der mit dem Zirkel auf die gewünschte Weise, hier in 8 Teile, geteilt wird. Hierauf sind von den Teilungspunkten senkrechte Linien bis E G und von da Linien parallel mit E e und G g, d. h. nach P bis zur Linie des unteren Halbkreises gezogen. Das Weitere ist aus der Figur ersichtlich, vgl. die Teilung eines verkürzten Kreises in 8 oder 6 Teile, Fig. 100–104.

Verkürzte Achtecke.

§ 93. Wie Fig. 97 zeigt, entsteht ein Achteck, wenn dieselben 8 Punkte, welche zur Darstellung des Kreises dienten, durch gerade Linien verbunden werden, nämlich die Halbierungspunkte der Seiten eines Quadrats und die Punkte seiner Diagonalen, welche von einem in demselben beschriebenen Kreis durchschnitten werden. Die perspectivische Form eines verkürzten Achtecks, welches die in Fig. 97 angenommene Stellung zu den Seiten eines gegebenen Quadrats hat, bedarf also keiner weiteren Erklärung.

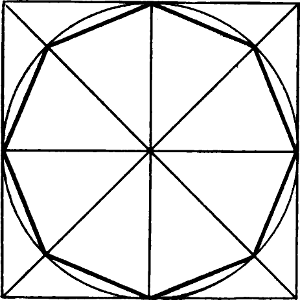
Etwas Anderes ist es, wenn ein Quadrat oder eine Seite eines Quadrats gegeben ist, in welchem ein Achteck wie a b c d e f g h in A B C D Fig. 98 gezeichnet werden soll, d. h. so, dass sämtliche 8 Ecken in den 4 Seiten des Quadrats liegen. Die geometrische Construction würde darin bestehen, dass die[123] 4 von i, dem Mittelpunkte des gegebenen Quadrats, nach den Halbierungspunkten der Seiten gehenden Linien über diese hinaus um soviel verlängert würden, dass jede die Länge einer halben Diagonale des Quadrats hätte, also i m, i n, i o und i p je = i A wären. Durch Verbindung der Punkte m, n, o und p entsteht ein zweites dem ersten gleiches Quadrat und die Verbindungslinien der Punkte b und c, d und e, f und g, h und a ergeben das Achteck.

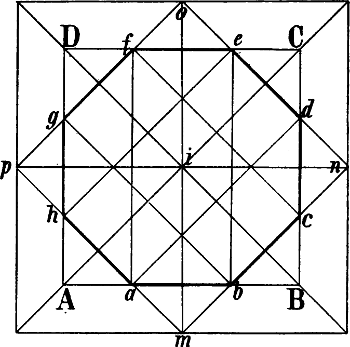
Ist nun das verkürzte Quadrat A B C D Fig. 99 gegeben, so kann eine der unverkürzten Seiten z. B. C D benüzt werden, um mit einer Hälfte derselben ein gleichschenkliges Dreieck C E F zu bilden. Wird hierauf E k = E F gemacht, so ist[124] das äussere Quadrat H G K L leicht zu bilden: eine Linie von P durch k schneidet die verlängerten Diagonalen A C und D B in H und G und 2 unverkürzte Wagrechte von hier aus ergeben die Punkte L und K. Hiermit sind auch die Punkte m, n, o und p und die Seiten des Achtecks gegeben.

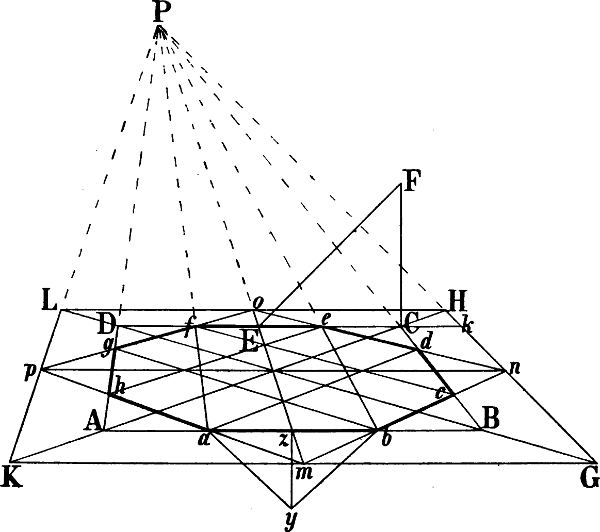
Oder könnte auch die Länge E F von C nach f und von D nach e getragen werden – denn aus Fig. 98 ist ersichtlich, dass C f oder D e = C i sind – um hierauf die weiteren Constructionslinien teils parallel mit den Diagonalen, teils parallel mit den Seiten des Quadrats A B C D zu ziehen.

Wäre statt des Quadrats A B C D a b als Seite eines zu zeichnenden Achtecks gegeben, so würde man mit der Hälfte derselben ein gleichschenkliges rechtwinkliges Dreieck b z y bilden, b B und a A = y b machen und hierauf das Quadrat A B C D construieren, um wie oben zu verfahren; vgl. die geometrische Zeichnung Fig. 98.7

§ 94. Fig. 100 zeigt die Construction eines Achtecks, wenn ein solches anschliessend an die Seiten eines Quadrats in schräger Ansicht gezeichnet werden soll.

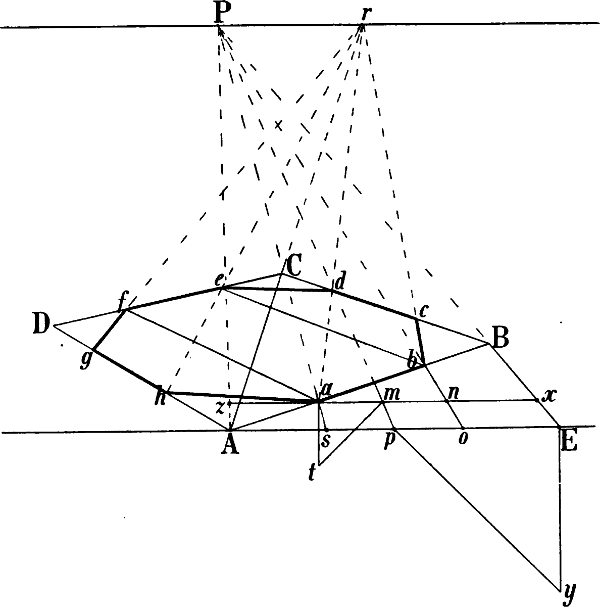
Angenommen, es sei das Quadrat A B C D gegeben, so ziehe man eine unverkürzte Wagrechte durch A und eine Linie von P durch B nach E. Die perspectivischen Verhältnisse, in welche A B zu teilen ist, können nun auf A E geometrisch angegeben und durch Linien, welche mit E B parallel sind, auf A B übertragen werden (vgl. Fig. 72 und 75). Man bildet entsprechend Fig. 98 mit der Hälfte von A E ein gleichschenkliges Dreieck p E y, macht A o und E s je = p y und zieht von s und o zwei mit E B parallele Linien nach a und b. Zieht man nun von a und von b aus zwei Linien nach r, dem Fluchtpunkte der Diagonale A C, zwei weitere parallel mit A D und[125] B C, so erhält man die Punkte c, d, e und f, durch eine Linie von r durch f den Punkt g und ist schliesslich noch die mit B D und e d parallele Seite a h zu zeichnen.

Der Augpunkt ist übrigens nur zufällig benüzt; es könnte statt desselben ein beliebiger Punkt des Horizonts gewählt werden.

Nehmen wir an, dass a b Fig. 100 als Seite eines zu zeichnenden Achtecks gegeben sei, so wäre das Verfahren ein ähnliches wie oben: von P (oder einem andern Punkte des Horizonts) wird eine Linie nach der durch a gehenden Wagrechten gezogen,[126] a n in m halbiert, ein gleichschenkliges rechtwinkliges Dreieck a m t gebildet und n x sowie a z je = m t gemacht. Die von P nach x und durch z gezogenen Linien ergeben die Punkte A und B, es kann nun mit A B das Quadrat A B C D gebildet werden u. s. w.

§ 95. Es kann auch der Fall eintreten, dass ein verkürzter Kreis gegeben ist und innerhalb desselben von einem bestimmten Punkte aus ein Achteck gezeichnet werden soll.

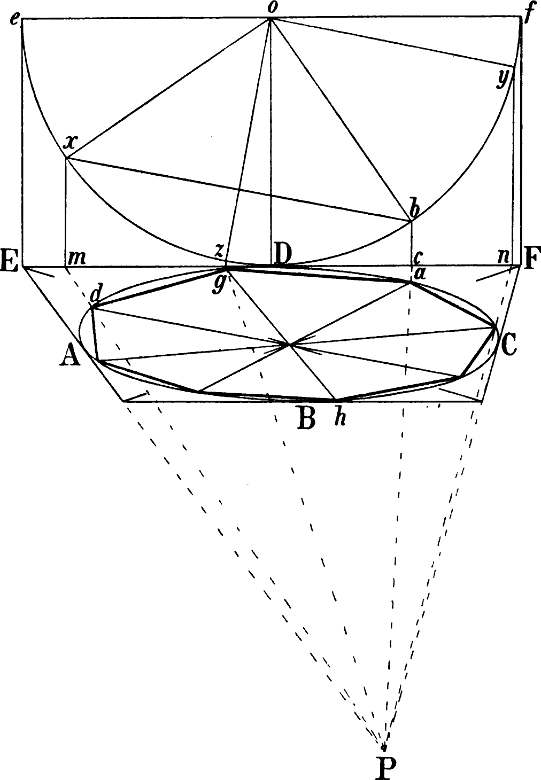
Es sei z. B. die Aufgabe gestellt, in dem verkürzten Kreise A B C D Fig. 101 von dem Punkte a aus ein Achteck zu zeichnen. o D ist = D F gemacht, mit der Zirkelweite D F von o aus ein Halbkreis e D f beschrieben und eine Linie von P durch a nach c gezogen; o x wird rechtwinklig zu o b, durch die Mitte von b x der Halbmesser o z und rechtwinklig zu diesem o y gezogen (vgl. Fig. 97), worauf die Punkte x y z mittels senkrechter Linien nach E F gebracht und von hier durch die aus m, n und dem Punkte zwischen z und g nach P gezogenen Linien auf den Kreis übertragen werden. Die 4 jenseitigen Punkte sind durch den Mittelpunkt des Kreises, beziehungsweise den Schnittpunkt der Diagonalen des Quadrats, gegeben.

Verkürzte Sechsecke.

§ 96. Die geometrische Construction eines Sechsecks besteht darin, dass ein Kreis in 6 Teile geteilt wird, von welchen jeder die Grösse eines Halbmessers jenes Kreises hat: man gibt – Fig. 102 – dem Zirkel die Weite eines Halbmessers z. B. O B, schneidet von B aus den Kreis in C, von C aus in D u. s. w. und verbindet diese Punkte durch gerade Linien. Zieht man von den 6 Ecken Linien nach dem Mittelpunkt O, so entstehen 6 gleichseitige Dreiecke; schliesst man das Sechseck in ein Rechteck, wie H K M N ein, so sind die beiden längeren Seiten je = 2 Seiten des Sechsecks: H K ist gleich 2 mal A B, H G = A B; H A, A G, G B und B K sind gleich gross. Die kürzeren Seiten sind je = 2 mal G O; H F und F N sind je = G O.

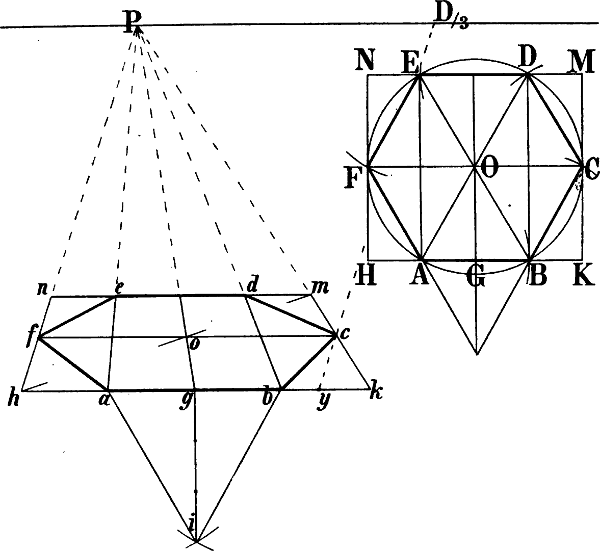
Ist nun a b als Seite eines verkürzten Sechsecks, P als Augpunkt und D/₃ als Drittel der Distanz gegeben, so wird b k und a h je = der Hälfte von a b gemacht, ein gleichseitiges[129] Dreieck a i b gebildet (indem von a und b aus 2 Kreise mit der Zirkelweite a b beschrieben werden, welche sich in i schneiden) und k c = g i gemacht durch eine Linie aus D/₃, nach y (k y = ein Drittel von g i). Hiemit sind das Rechteck h k m n und die weiteren Punkte d, e und f gegeben.

§ 97. In Fig. 103 ist angenommen, dass h n als kürzere Seite des von unten gesehenen Rechtecks, P als Augpunkt und D/₂ als halbe Distanz gegeben sei, in f also eine Ecke des Sechsecks liege. Beschreibt man von n und von f aus zwei[130] Kreisbögen mit der Zirkelweite n f, so schneiden sich dieselben in s und es entsteht, indem durch s eine rechtwinklig zu f s stehende Linie bis zu den in f und n errichteten Senkrechten gezogen wird, ein gleichseitiges Dreieck, dessen Mittellinie s f = f n oder = f h ist, dessen Seiten also (vgl. § 96, Fig. 102) auf die durch f gehende Wagrechte übertragen, die Länge einer Seite des zu zeichnenden Sechsecks darstellen. h p ist = f z; die von h nach P gehende Seite des zu bildenden Rechtecks muss also = 2 mal h p sein (wie H K Fig. 102 = 2 mal A B ist), was durch eine Linie von D/₂ nach p erreicht wird. Ist so das Verhältnis der Seiten in dem Rechteck h k m n das gleiche, wie in H K M N Fig. 102, so bleibt nur noch übrig, dasselbe mittels Diagonalen wie dort in 4 gleiche Teile zu teilen, um die weiteren Ecken zu erhalten.

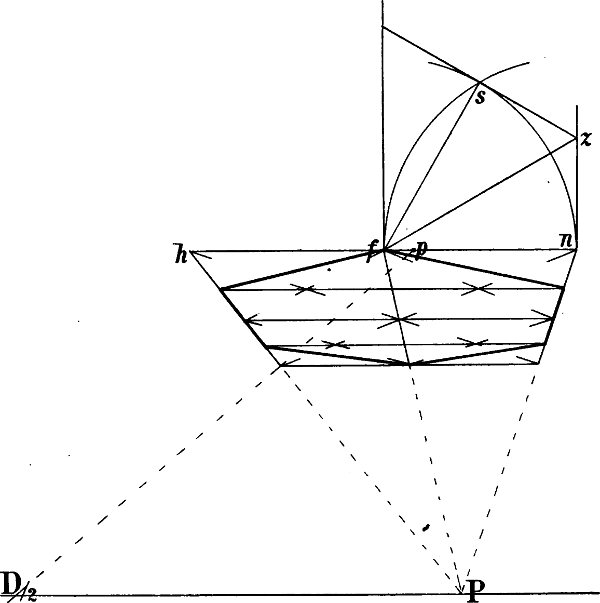
§ 98. In Fig. 104 soll von dem Punkte d des Kreises A B C D aus ein Sechseck gezeichnet werden. Das Quadrat des Kreises ist E F G H. Wie in Fig. 101 ist E e und F f = der Hälfte von E F gemacht und von o aus ein Halbkreis beschrieben, auf welchem x dem Punkte d des verkürzten Kreises entspricht (mittels P d m und m x). Von x aus schneidet der Zirkel mit der Weite eines Halbmessers D o oder x o den Halbkreis in b, von hier aus in y, und diese beiden Punkte werden auf die mehrfach beschriebene Weise nach a und c übertragen; Linien aus d, a und c durch den Mittelpunkt des Quadrats gezogen, ergeben die 3 jenseitigen Ecken.

Weitere Beispiele. Rad, Wasserrad, Walze, Cylinder.

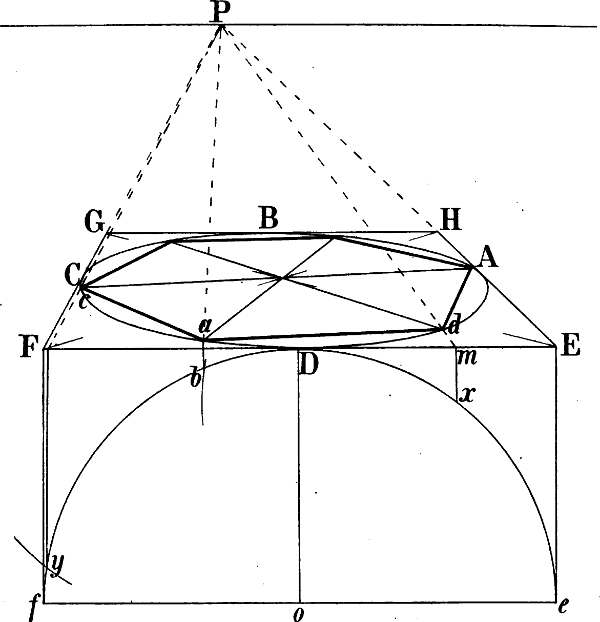
§ 99. Fig. 105 zeigt die Anwendung von § 91 Fig. 95 auf 2 durch eine Achse verbundene Räder. Der Deutlichkeit wegen sind hier sowie in der folgenden Figur nur die wichtigsten Constructionslinien angegeben, mit deren Hilfe das Übrige ohne[131] Schwierigkeit, so genau als der malerische Zweck erfordert, ergänzt werden kann.

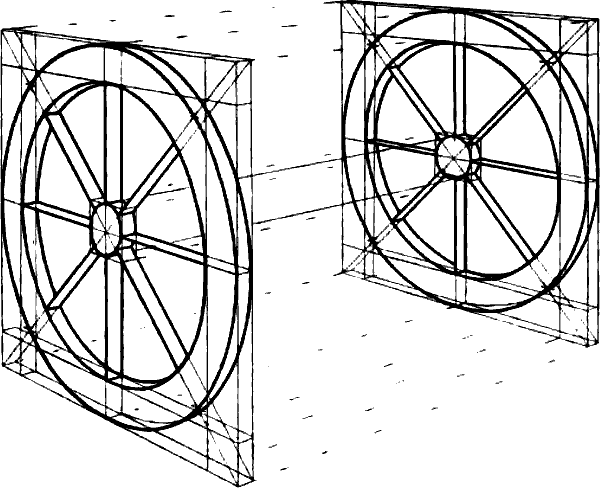
In Fig. 106 sind zunächst die 4 Kreise entsprechend Fig. 95 und 96 gezeichnet. Hierauf ist der durch a b c gehende Halbkreis in 5 gleiche Teile geteilt und diese Teilung auf die andere Hälfte übertragen (vgl. Fig. 101 und 104), indem nach dem Halbkreis c d a Linien von jenen Teilpunkten aus durch den Mittelpunkt gezogen wurden. Diese Linien ergeben zugleich die Stellung der einzelnen Schaufeln; die wagrechten Linien der lezteren sind parallel mit e f, g h und o n; die Verbindungslinien der Punkte i und k, y und z u. s. w. gehen durch den Mittelpunkt n.

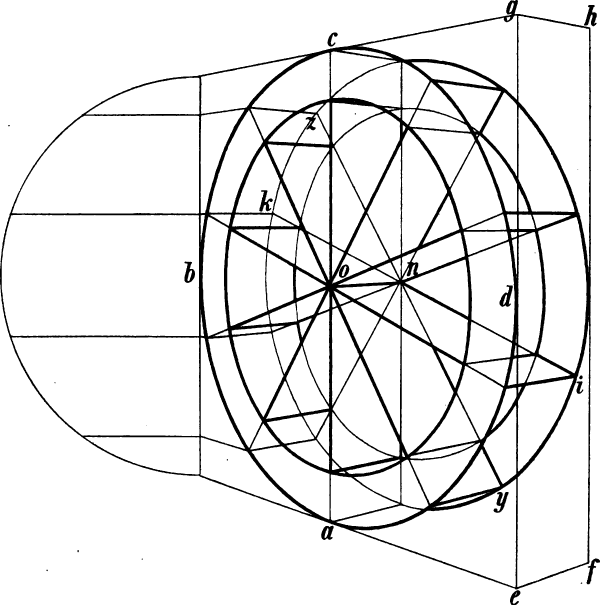
§ 100. In Fig. 107 ist der Kreis a b c d als vorderer Durchschnitt einer wagrecht liegenden Walze angenommen. Da derselbe unverkürzt ist und die durch i gehende Achse der Walze[132] geometrisch rechtwinklig zu d b steht, so sind von d und b 2 Linien nach dem Augpunkt gezogen und dieselben an beliebiger Stelle durch die Wagrechte h f verbunden. Ein Kreis aus o, der Mitte von h f, durch h und f beschrieben, ergibt e f g h als den ferner liegenden Durchschnitt, worauf vom Augpunkt aus 2 die beiden Kreise berührende Linien (Tangenten) parallel mit i o als Aussenlinien der Walze gezogen werden.

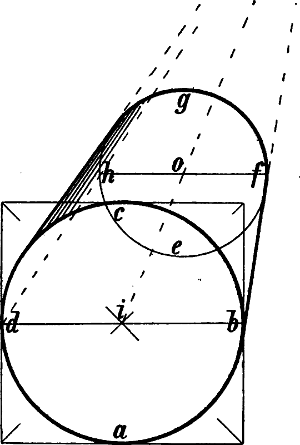
Um den Cylinder Fig. 108 zu construieren, sind den beiden vorderen Kreisen entsprechend auf die oben gezeigte Weise die beiden ferneren zu zeichnen.

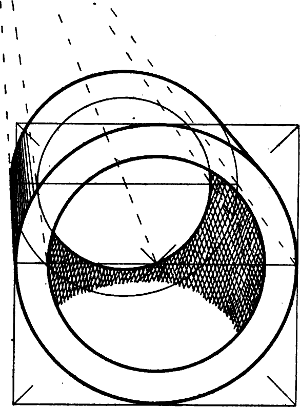
Dieselben Formen mit verkürzter Ansicht des Kreises zu zeichnen, bietet hienach keine Schwierigkeit. Man achte dabei auf die bereits erwähnte geometrisch rechtwinklige Stellung der Achse und der Seitenlinien zur Kreisfläche, beziehungsweise zu einem Durchmesser derselben.

Tonnengewölbe, Kreuzgewölbe, Spizbogen, Kuppel.

§ 101. Fig. 109 stellt ein sogenanntes Tonnengewölbe dar. Dasselbe hat die Form eines halben Cylinders, welcher in Fig. 109 auf den nach dem Augpunkt gehenden Linien a e und b f ruht. Die Construction besteht einfach darin, dass über a b und e f je ein Halbkreis von den Mittelpunkten c und d aus beschrieben wird. Die Fugenlinien des Gewölbes gehen teils parallel mit a e und b f, teils sind sie Teile von Halbkreisen, welche mit den beiden ersteren parallel sind, deren[134] Mittelpunkte somit in der Linie c d liegen. So ist der Mittelpunkt des Halbkreises m n p da, wo die Wagrechte m p von c d durchschnitten wird, in o. Die Fugenlinien g h, i k u. s. w. haben die Richtung nach c, dem Mittelpunkt der beiden durch k h und i g gehenden Halbkreise.

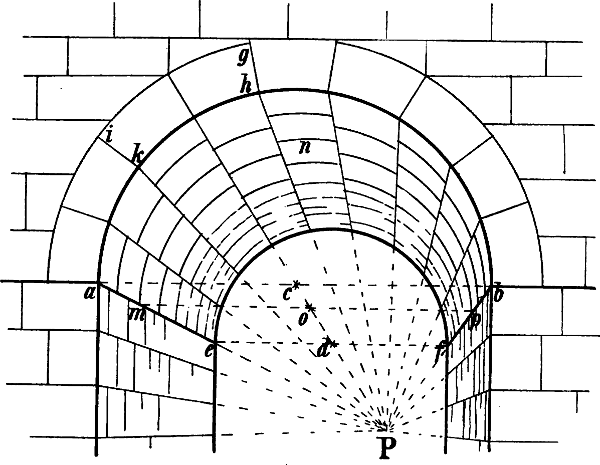
§ 102. Fig. 110 zeigt die Hauptlinien eines von aussen und oben gesehenen rundbogigen Kreuzgewölbes. A B C D ist ein Quadrat; über jeder Seite desselben erhebt sich ein Halbkreis, die gegenüberliegenden Ecken des Quadrats, A und C, B und D, sind nach oben verbunden durch 2 elliptische Linien, die sogenannten Diagonalrippen oder -gurten, welche sich über den Diagonalen A C und B D hinziehen. Der Scheitelpunkt n des Gewölbes, in welchem die beiden Ellipsen sich durchschneiden, liegt senkrecht über der Kreuzung der Diagonalen A C und B D, er ist zugleich Schnittpunkt der Diagonalen[135] E z und F t. Es entstehen so 4 Gewölbefelder oder Kappen, welche je von einem Halbkreis und 2 Hälften jener Ellipsen begrenzt werden, z. B. von A m B, A n und B n, vgl. die innere Ansicht Fig. 111–113.

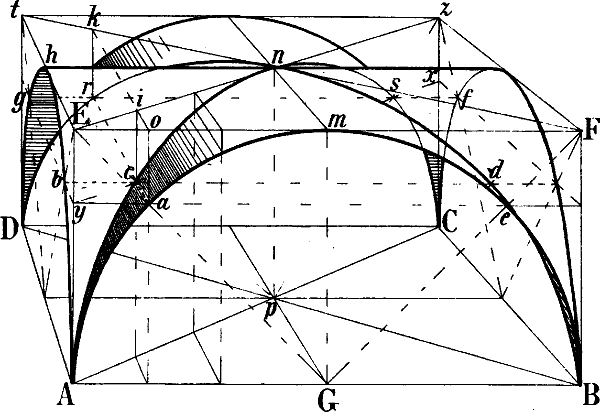
Bei der perspectivischen Construction einer solchen Gewölbeform handelt es sich, nachdem über jeder Seite des zu Grunde gelegten Quadrats ein Halbkreis gezeichnet ist, hauptsächlich um die Bestimmung einiger weiteren Hilfspunkte ausser dem durch E z und F t gegebenen Punkte n behufs Darstellung der beiden elliptischen Linien. Die Halbkreise A m B und A h D werden von 2 Linien, welche man aus E nach der Mitte von A B und von A D zieht, in a und in b geschnitten. Diese beiden Punkte liegen in gleicher Höhe; zieht man aus a eine Linie parallel mit A D, also nach dem Augpunkt, und aus b eine Parallele mit A B, d. h. eine unverkürzte Wagrechte, so müssen diese beiden Linien in dem Punkte c der von A ausgehenden Ellipse A n C zusammentreffen, welcher mit a und b[136] in gleicher Höhe liegt und kann somit dieser Punkt benuzt werden, um A c n zu zeichnen.

Dem Punkte a entspricht auf der rechten Seite e, eine Linie von hier nach dem Augpunkt und eine Wagrechte aus c schneiden sich in d. Die entsprechenden jenseitigen Punkte der beiden Ellipsen ergeben sich durch die aus a und e nach dem Augpunkt gehenden Linien und eine Wagrechte von g nach f oder umgekehrt.

§ 103. Fig. 111 zeigt dieselben Linien von unten und von innen gesehen, mit dem Unterschied, dass die 2 Seitenkappen geschlossen bis A D und B D herabgehen (wie auch in Fig. 113). Der Fluchtpunkt dieser und der mit ihnen parallelen Linien ist wiederum der Augpunkt; A B, C D und[137] die beiden Halbkreise sind unverkürzt. Um die beiden Diagonalgurten zu zeichnen, ist hier ein anderer Weg eingeschlagen. In Fig. 110 liegen die Punkte y und x in gleicher Höhe mit a, b und f. Zieht man von y eine mit A C und E z parallele Linie nach x, von E und z 2 Linien nach p, so erhält man da, wo die Linie y x von E p und z p geschnitten wird, gleichfalls die Punkte c und s, welche nun mittels unverkürzter Wagrechter nach d und r übertragen werden können.

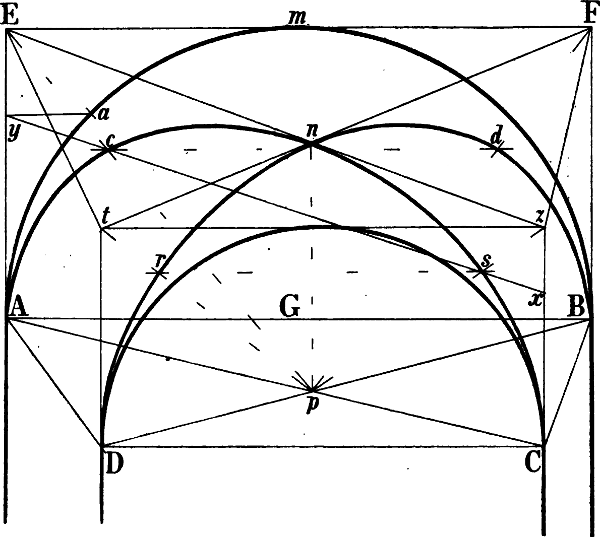
In Fig. 111 entspricht das senkrecht stehende von unten gesehene Rechteck E A C z dem Rechteck E A C z in Fig. 110; auch die übrigen einander entsprechenden Punkte beider Figuren sind durch dieselben Buchstaben bezeichnet. Der Halbkreis A m B wird von der Diagonale E G in a geschnitten. Zieht man von a eine Wagrechte nach y und von y eine mit E z parallele Linie nach x, so erhält man durch E p und z p die Punkte c und s u. s. w.

§ 104. In Fig. 112 ist von einem beliebigen Punkte a des Halbkreises A m B eine Senkrechte nach o und von hier eine Linie parallel mit E y d. h. nach dem Augpunkt gezogen,[138] welche die Diagonalen des Quadrats E F z y in i und k schneidet. Zieht man nun von i und k 2 Senkrechte nach der aus a nach dem Augpunkt gehenden Linie, so erhält man die Punkte c und r, vgl. dieselben Punkte in Fig. 110.

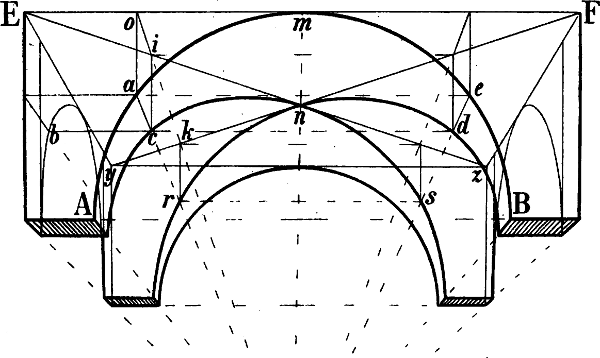
Durch eine Wagrechte aus a nach e, eine Linie von e nach dem Augpunkt und 2 Wagrechte aus c und r ergeben sich sodann d und s.

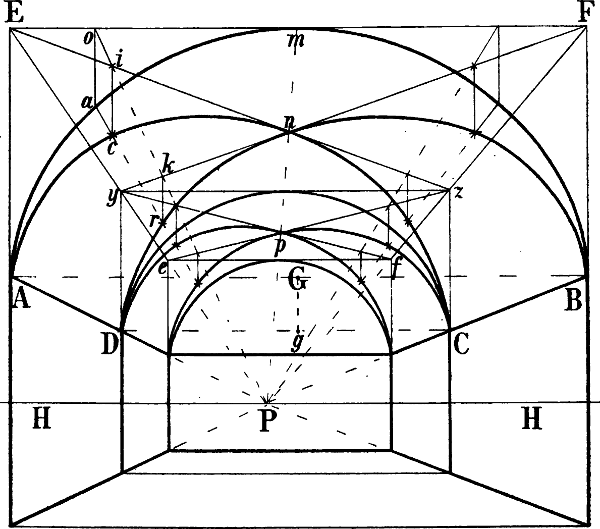
Wenn die seitlichen Kappen, wie in Fig. 113, geschlossen bis auf die wagrechte Linie herabgehen, auf welcher das Gewölbe ruht, so ist das leztgenannte Verfahren bequemer als das in § 102 beschriebene. Die Anwendung desselben auf Fig. 113 ist aus den Constructionslinien zu ersehen. A m B ist hier nicht ein[139] Halbkreis, sondern ein flacher Bogen, ein sogenannter Korbbogen. Der obere Teil desselben ist aus dem senkrecht unter G liegenden Punkte g beschrieben, die Fortsezung bis A und B kann leicht aus freier Hand ergänzt werden.

§ 105. Ein Spizbogen wird gebildet durch 2 sich durchschneidende Bögen, wie A, B, C Fig. 114 zeigen. In A sind die beiden Bögen von a und von b aus mit der Zirkelweite a b beschrieben, in B von den Punkten m und n aus mit der Weite m c, in C von o und i aus mit der Weite i e (m d = n c, o e = i f). Die den Spizbogen umgebenden Fugenlinien haben die Richtung nach dem Mittelpunkte des betreffenden Bogens: in A nach a und b, in B nach m und n, in C nach i und o.

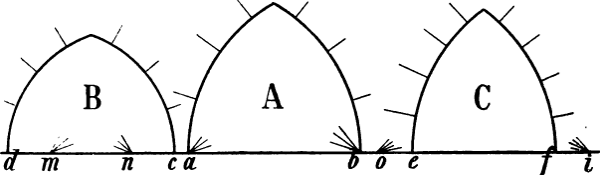
Sind mehrere in einer Flucht liegende Spizbögen in verkürzter Stellung zu zeichnen, so bilde man das Rechteck eines Spizbogens z. B. a b c d Fig. 115 und ziehe in demselben die senkrechte Mittellinie. Man kann nun eine der Bogenlinien z. B. a B (leichter als b B) aus freier Hand zeichnen und den Punkt o, in welchem sie von der Diagonale A d geschnitten wird, mittels e f, A c, g C u. s. w. nach n, m u. s. w. übertragen, was für gewöhnlich genügen wird. Ist grössere Genauigkeit erforderlich, so kann mit Hilfe eines Distanzpunktes anschliessend an a d ein unverkürztes Rechteck a d z y gebildet und a h als geometrische Form der anstossenden unverkürzten Bogenlinie gezeichnet werden, worauf der Punkt i nach e und von hier nach o, n, m u. s. w. übertragen wird.

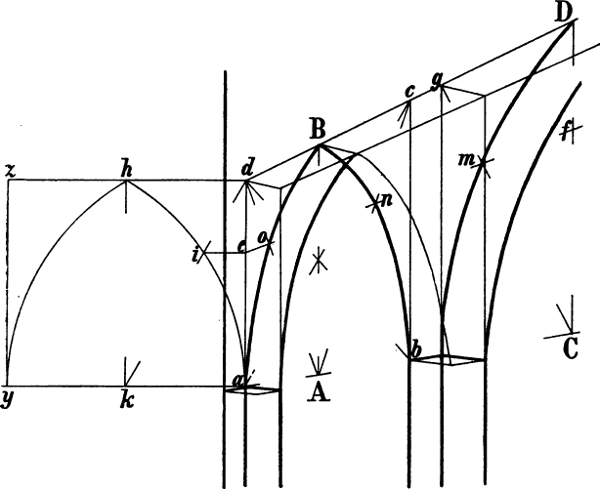
§ 106. Als Beispiel eines spizbogigen Kreuzgewölbes ist in Fig. 116 der Deutlichkeit wegen die einfachste Form eines solchen gewählt; es wird jedoch nicht schwierig sein, das dabei angewandte Verfahren auf andere Formen, welche sehr mannigfaltiger Art sein können, anzuwenden. Die Mittelpunkte der Bogen A m und B m, D o und C o sind in a und b, e und f. A a ist ein Viertel von A B, A B C D ist ein Quadrat. A i ist = A B; eine Linie von B nach i stellt also die geometrische Länge der Diagonale A C dar. Es ist nun ein Rechteck G H h g gebildet, in welchem G H = B i = A C und G g = A E ist; G H h g ist somit die geometrische Form des verkürzten Rechtecks A E z C; der von g nach h führende Bogen ist = der von A nach C führenden Diagonalrippe. Da G g[141] die Hälfte von G H ist, so ergibt sich, dass jene Diagonalrippe ein Halbkreis ist. Wird nun E y = G k gemacht, so kann die Lage der Punkte c, s, d und r wie bei Fig. 111 bestimmt werden.

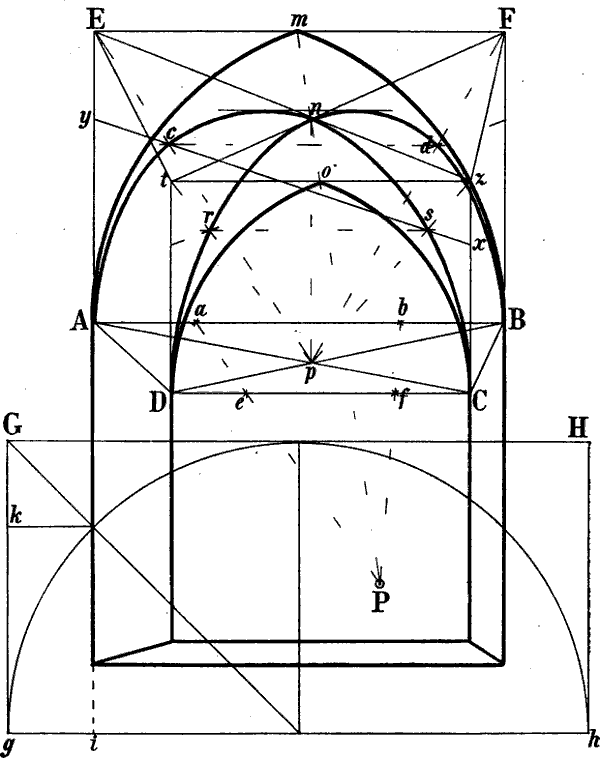
§ 107. Fig. 117 zeigt eine von oben gesehene, in 8 Felder geteilte Halbkugel. Der ihren äusseren Umriss bildende Halbkreis ist mit dem Zirkel vom Mittelpunkt der Linie A a aus beschrieben. Indem die Linien A i und a i zugleich als Teilungslinien angenommen wurden, ergeben sich die weiteren Teilpunkte der durch A und a gehenden Kreislinie, nämlich B, C, D, b, c und d, durch die Halbierungslinie und Diagonale des jenen Kreis umschliessenden Quadrats, und es stellt sich der von C durch i nach c führende Halbkreis als Eine senkrechte Linie dar. Um die verkürzten Halbkreise B m o b und D n p d zu zeichnen, ist das Quadrat E F G H (E B = der[143] Hälfte von B D) senkrecht über B D b d gebildet, in welchem die auf bekannte Weise bestimmten Punkte m, n, o, p als Hilfspunkte für jene Halbkreise dienen.

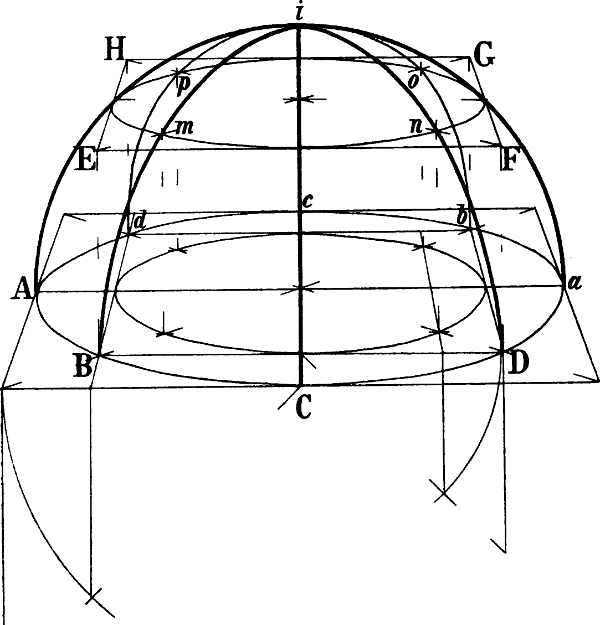
§ 108. In Fig. 118 sei der durch A B C D gehende Kreis und in diesem der Punkt B gegeben, um von hier aus eine[144] achtseitige eiförmige Kuppel und darüber eine gleichfalls achtseitige Laterne zu zeichnen.

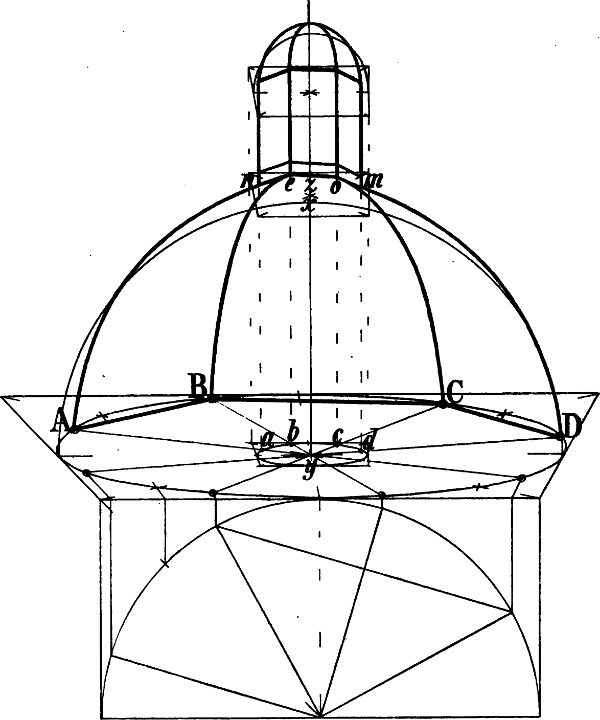
Die Teilung des Kreises in 8 Teile ist in § 95 Fig. 101 gezeigt. Die Ausführung in Fig. 118 ist nur insofern verschieden, als hier die Constructionslinien an die fernere Linie des den Kreis einschliessenden Quadrats nach unten angefügt sind. Sodann ist entsprechend dem Umfang, welchen die Laterne haben soll, ein kleinerer Kreis von demselben Mittelpunkt y aus gezeichnet, welcher durch den von A, B, C, D nach y gehenden Halbmessern in den Punkten a b c d geschnitten wird. Die in a b c d errichteten Senkrechten bilden die Ecklinien der 3 sichtbaren Seiten der Laterne, welche oben und unten durch Parallelen der Linien A B, B C und C D begrenzt sind. Die Linien A n, B e, C o und D m treffen in ihrer Verlängerung zusammen in einem Punkte der senkrechten Mittellinie, hier in z, und es ist zu beachten, dass dieser Punkt bei einer derartigen Kuppelform höher liegen muss, als der Mittelpunkt des Kreises, welcher durch n, e, o, m geht, hier also höher, als x.

Fußnoten

1 Anm. Das Notwendigste und zugleich Einfachste sind ausser einigen Grundbegriffen (§§ 1–15) die allgemeinen Regeln über die Richtung der verkürzten parallelen und wagrechten Linien (§§ 20–29, § 37); nächst diesen die §§ 30–36, 41–64, 71–73, 86–92, 99–101, § 105. Der Grad von perspectivischer Genauigkeit, welcher mit Hilfe dieser Abschnitte zu erzielen ist, mag in vielen Fällen genügen.

2 Mit dem Ausdruck »Bild« wird sowohl der perspectivisch gesehene Gegenstand selbst, als die perspectivische Darstellung desselben bezeichnet.

3 Man könnte aus der Kugelgestalt der Erde schliessen, dass die Grenzlinie der Meeresfläche oder einer grossen Ebene nicht eine gerade Linie sei und nicht genau in der Höhe des Auges liege. Aber im Verhältnis zur Grösse des Erdballs ist der Teil, welchen wir mit Einem Blick übersehen können, so klein, dass er wie eine wagrechte Fläche, seine Grenzlinie vollständig wagrecht erscheint und angenommen werden kann, dass leztere in gleicher Höhe mit dem Auge liege.

4 Ein geschickter Zeichner mag sich allerdings zuweilen Abweichungen von dieser wie von andern Regeln gestatten, aber um zu wissen, wo und wie er dies thun kann, ohne dass die Wirkung seiner Zeichnung eine falsche oder zum mindesten unschöne wird, muss er vor allem die Regel kennen, welche hiedurch nichts an ihrer Giltigkeit verliert.

5 In einer senkrechten Fläche können sowohl senkrechte als wagrechte und schräge Linien liegen, in einer schrägen Fläche nur schräge und wagrechte, in einer wagrechten Fläche nur wagrechte Linien, vgl. die Flächen A, D und C, Fig. 19.

6 Statt des bei k und D stehenden Buchstaben b ist ein t zu sezen.

7 Fig. 99 ist insofern ungenau, als b B und a A etwas kleiner sind als y b. Der Fehler wurde zu spät bemerkt und ist so geringfügig, dass es genügen dürfte, hiedurch darauf aufmerksam zu machen.

Weitere Anmerkungen zur Transkription

Offensichtliche Satzfehler und fehlende Auszeichnungen wurden stillschweigend korrigiert.

Die Abbildungen wurden soweit wie möglich zu den entsprechenden Paragraphen verschoben.

Die Korrekturliste von S. VIII wurde eingearbeitet, diese Korrekturen sind hier einzeln aufgeführt.

Der doppelte Paragraph § 92 wurde beibehalten.

Die Seitennummern der ganzseitigen Illustrationen (13, 16, 18, 25, 35, 54, 56, 68, 85, 102, 110, 112, 114, 128) wurden entfernt.

Korrekturen:

Seite V: Bedürfniss → Bedürfnis
haben dem Verfasser das Bedürfnis

Seite VIII: paralleller → paralleler, Größenverhältniss → Grössenverhältnis
Perspectivisches Grössenverhältnis nicht paralleler Linien

S. 4: Sachlicher Fehler (nicht korrigiert):
Die beiden Diagonalen eines Parallelogramms sind gleich lang,

S. 17: desto schmaler, je höher wir stehen ergänzt
je tiefer wir stehen, desto schmaler, je höher wir stehen, desto breiter erscheint uns dieselbe,

S. 26: a d und b c vertauscht
da b c ferner liegt als a d,

S. 50: g → B
und zieht von B durch p eine Linie

S. 57: E → F
Oder kann von F eine mit D E parallele

S. 62: m d → n a
d h ist = n a gemacht

S. 72: b → B
Mitte eines Quadrats (A B p f)

S. 99: die → der
so ist b f = die Hälfte von B b;

S. 122: Atwas → Etwas
Etwas Anderes ist es,

S. 133: Coustruction → Construction
Die Construction besteht einfach darin,

S. 135: y → t
dem durch E z und F t gegebenen Punkte n

S. 136: ruht nach vorn verschoben
auf welcher das Gewölbe ruht,

*** END OF THE PROJECT GUTENBERG EBOOK LEHRBUCH DER PERSPECTIVE ***

Updated editions will replace the previous one—the old editions will be renamed.

Creating the works from print editions not protected by U.S. copyright law means that no one owns a United States copyright in these works, so the Foundation (and you!) can copy and distribute it in the United States without permission and without paying copyright royalties. Special rules, set forth in the General Terms of Use part of this license, apply to copying and distributing Project Gutenberg™ electronic works to protect the PROJECT GUTENBERG™ concept and trademark. Project Gutenberg is a registered trademark, and may not be used if you charge for an eBook, except by following the terms of the trademark license, including paying royalties for use of the Project Gutenberg trademark. If you do not charge anything for copies of this eBook, complying with the trademark license is very easy. You may use this eBook for nearly any purpose such as creation of derivative works, reports, performances and research. Project Gutenberg eBooks may be modified and printed and given away—you may do practically ANYTHING in the United States with eBooks not protected by U.S. copyright law. Redistribution is subject to the trademark license, especially commercial redistribution.

START: FULL LICENSE

PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK

To protect the Project Gutenberg™ mission of promoting the free distribution of electronic works, by using or distributing this work (or any other work associated in any way with the phrase “Project Gutenberg”), you agree to comply with all the terms of the Full Project Gutenberg™ License available with this file or online at www.gutenberg.org/license.

Section 1. General Terms of Use and Redistributing Project Gutenberg™ electronic works

1.A. By reading or using any part of this Project Gutenberg™ electronic work, you indicate that you have read, understand, agree to and accept all the terms of this license and intellectual property (trademark/copyright) agreement. If you do not agree to abide by all the terms of this agreement, you must cease using and return or destroy all copies of Project Gutenberg™ electronic works in your possession. If you paid a fee for obtaining a copy of or access to a Project Gutenberg™ electronic work and you do not agree to be bound by the terms of this agreement, you may obtain a refund from the person or entity to whom you paid the fee as set forth in paragraph 1.E.8.

1.B. “Project Gutenberg” is a registered trademark. It may only be used on or associated in any way with an electronic work by people who agree to be bound by the terms of this agreement. There are a few things that you can do with most Project Gutenberg™ electronic works even without complying with the full terms of this agreement. See paragraph 1.C below. There are a lot of things you can do with Project Gutenberg™ electronic works if you follow the terms of this agreement and help preserve free future access to Project Gutenberg™ electronic works. See paragraph 1.E below.

1.C. The Project Gutenberg Literary Archive Foundation (“the Foundation” or PGLAF), owns a compilation copyright in the collection of Project Gutenberg™ electronic works. Nearly all the individual works in the collection are in the public domain in the United States. If an individual work is unprotected by copyright law in the United States and you are located in the United States, we do not claim a right to prevent you from copying, distributing, performing, displaying or creating derivative works based on the work as long as all references to Project Gutenberg are removed. Of course, we hope that you will support the Project Gutenberg™ mission of promoting free access to electronic works by freely sharing Project Gutenberg™ works in compliance with the terms of this agreement for keeping the Project Gutenberg™ name associated with the work. You can easily comply with the terms of this agreement by keeping this work in the same format with its attached full Project Gutenberg™ License when you share it without charge with others.

1.D. The copyright laws of the place where you are located also govern what you can do with this work. Copyright laws in most countries are in a constant state of change. If you are outside the United States, check the laws of your country in addition to the terms of this agreement before downloading, copying, displaying, performing, distributing or creating derivative works based on this work or any other Project Gutenberg™ work. The Foundation makes no representations concerning the copyright status of any work in any country other than the United States.

1.E. Unless you have removed all references to Project Gutenberg:

1.E.1. The following sentence, with active links to, or other immediate access to, the full Project Gutenberg™ License must appear prominently whenever any copy of a Project Gutenberg™ work (any work on which the phrase “Project Gutenberg” appears, or with which the phrase “Project Gutenberg” is associated) is accessed, displayed, performed, viewed, copied or distributed:

This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you will have to check the laws of the country where you are located before using this eBook.

1.E.2. If an individual Project Gutenberg™ electronic work is derived from texts not protected by U.S. copyright law (does not contain a notice indicating that it is posted with permission of the copyright holder), the work can be copied and distributed to anyone in the United States without paying any fees or charges. If you are redistributing or providing access to a work with the phrase “Project Gutenberg” associated with or appearing on the work, you must comply either with the requirements of paragraphs 1.E.1 through 1.E.7 or obtain permission for the use of the work and the Project Gutenberg™ trademark as set forth in paragraphs 1.E.8 or 1.E.9.

1.E.3. If an individual Project Gutenberg™ electronic work is posted with the permission of the copyright holder, your use and distribution must comply with both paragraphs 1.E.1 through 1.E.7 and any additional terms imposed by the copyright holder. Additional terms will be linked to the Project Gutenberg™ License for all works posted with the permission of the copyright holder found at the beginning of this work.

1.E.4. Do not unlink or detach or remove the full Project Gutenberg™ License terms from this work, or any files containing a part of this work or any other work associated with Project Gutenberg™.

1.E.5. Do not copy, display, perform, distribute or redistribute this electronic work, or any part of this electronic work, without prominently displaying the sentence set forth in paragraph 1.E.1 with active links or immediate access to the full terms of the Project Gutenberg™ License.

1.E.6. You may convert to and distribute this work in any binary, compressed, marked up, nonproprietary or proprietary form, including any word processing or hypertext form. However, if you provide access to or distribute copies of a Project Gutenberg™ work in a format other than “Plain Vanilla ASCII” or other format used in the official version posted on the official Project Gutenberg™ website (www.gutenberg.org), you must, at no additional cost, fee or expense to the user, provide a copy, a means of exporting a copy, or a means of obtaining a copy upon request, of the work in its original “Plain Vanilla ASCII” or other form. Any alternate format must include the full Project Gutenberg™ License as specified in paragraph 1.E.1.

1.E.7. Do not charge a fee for access to, viewing, displaying, performing, copying or distributing any Project Gutenberg™ works unless you comply with paragraph 1.E.8 or 1.E.9.

1.E.8. You may charge a reasonable fee for copies of or providing access to or distributing Project Gutenberg™ electronic works provided that:

• You pay a royalty fee of 20% of the gross profits you derive from the use of Project Gutenberg™ works calculated using the method you already use to calculate your applicable taxes. The fee is owed to the owner of the Project Gutenberg™ trademark, but he has agreed to donate royalties under this paragraph to the Project Gutenberg Literary Archive Foundation. Royalty payments must be paid within 60 days following each date on which you prepare (or are legally required to prepare) your periodic tax returns. Royalty payments should be clearly marked as such and sent to the Project Gutenberg Literary Archive Foundation at the address specified in Section 4, “Information about donations to the Project Gutenberg Literary Archive Foundation.”
• You provide a full refund of any money paid by a user who notifies you in writing (or by e-mail) within 30 days of receipt that s/he does not agree to the terms of the full Project Gutenberg™ License. You must require such a user to return or destroy all copies of the works possessed in a physical medium and discontinue all use of and all access to other copies of Project Gutenberg™ works.
• You provide, in accordance with paragraph 1.F.3, a full refund of any money paid for a work or a replacement copy, if a defect in the electronic work is discovered and reported to you within 90 days of receipt of the work.
• You comply with all other terms of this agreement for free distribution of Project Gutenberg™ works.

1.E.9. If you wish to charge a fee or distribute a Project Gutenberg™ electronic work or group of works on different terms than are set forth in this agreement, you must obtain permission in writing from the Project Gutenberg Literary Archive Foundation, the manager of the Project Gutenberg™ trademark. Contact the Foundation as set forth in Section 3 below.

1.F.

1.F.1. Project Gutenberg volunteers and employees expend considerable effort to identify, do copyright research on, transcribe and proofread works not protected by U.S. copyright law in creating the Project Gutenberg™ collection. Despite these efforts, Project Gutenberg™ electronic works, and the medium on which they may be stored, may contain “Defects,” such as, but not limited to, incomplete, inaccurate or corrupt data, transcription errors, a copyright or other intellectual property infringement, a defective or damaged disk or other medium, a computer virus, or computer codes that damage or cannot be read by your equipment.

1.F.2. LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the “Right of Replacement or Refund” described in paragraph 1.F.3, the Project Gutenberg Literary Archive Foundation, the owner of the Project Gutenberg™ trademark, and any other party distributing a Project Gutenberg™ electronic work under this agreement, disclaim all liability to you for damages, costs and expenses, including legal fees. YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE PROVIDED IN PARAGRAPH 1.F.3. YOU AGREE THAT THE FOUNDATION, THE TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH DAMAGE.

1.F.3. LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a defect in this electronic work within 90 days of receiving it, you can receive a refund of the money (if any) you paid for it by sending a written explanation to the person you received the work from. If you received the work on a physical medium, you must return the medium with your written explanation. The person or entity that provided you with the defective work may elect to provide a replacement copy in lieu of a refund. If you received the work electronically, the person or entity providing it to you may choose to give you a second opportunity to receive the work electronically in lieu of a refund. If the second copy is also defective, you may demand a refund in writing without further opportunities to fix the problem.

1.F.4. Except for the limited right of replacement or refund set forth in paragraph 1.F.3, this work is provided to you ‘AS-IS’, WITH NO OTHER WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO WARRANTIES OF MERCHANTABILITY OR FITNESS FOR ANY PURPOSE.

1.F.5. Some states do not allow disclaimers of certain implied warranties or the exclusion or limitation of certain types of damages. If any disclaimer or limitation set forth in this agreement violates the law of the state applicable to this agreement, the agreement shall be interpreted to make the maximum disclaimer or limitation permitted by the applicable state law. The invalidity or unenforceability of any provision of this agreement shall not void the remaining provisions.

1.F.6. INDEMNITY - You agree to indemnify and hold the Foundation, the trademark owner, any agent or employee of the Foundation, anyone providing copies of Project Gutenberg™ electronic works in accordance with this agreement, and any volunteers associated with the production, promotion and distribution of Project Gutenberg™ electronic works, harmless from all liability, costs and expenses, including legal fees, that arise directly or indirectly from any of the following which you do or cause to occur: (a) distribution of this or any Project Gutenberg™ work, (b) alteration, modification, or additions or deletions to any Project Gutenberg™ work, and (c) any Defect you cause.

Section 2. Information about the Mission of Project Gutenberg™

Project Gutenberg™ is synonymous with the free distribution of electronic works in formats readable by the widest variety of computers including obsolete, old, middle-aged and new computers. It exists because of the efforts of hundreds of volunteers and donations from people in all walks of life.

Volunteers and financial support to provide volunteers with the assistance they need are critical to reaching Project Gutenberg™’s goals and ensuring that the Project Gutenberg™ collection will remain freely available for generations to come. In 2001, the Project Gutenberg Literary Archive Foundation was created to provide a secure and permanent future for Project Gutenberg™ and future generations. To learn more about the Project Gutenberg Literary Archive Foundation and how your efforts and donations can help, see Sections 3 and 4 and the Foundation information page at www.gutenberg.org.

Section 3. Information about the Project Gutenberg Literary Archive Foundation

The Project Gutenberg Literary Archive Foundation is a non-profit 501(c)(3) educational corporation organized under the laws of the state of Mississippi and granted tax exempt status by the Internal Revenue Service. The Foundation’s EIN or federal tax identification number is 64-6221541. Contributions to the Project Gutenberg Literary Archive Foundation are tax deductible to the full extent permitted by U.S. federal laws and your state’s laws.

The Foundation’s business office is located at 809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887. Email contact links and up to date contact information can be found at the Foundation’s website and official page at www.gutenberg.org/contact

Section 4. Information about Donations to the Project Gutenberg Literary Archive Foundation

Project Gutenberg™ depends upon and cannot survive without widespread public support and donations to carry out its mission of increasing the number of public domain and licensed works that can be freely distributed in machine-readable form accessible by the widest array of equipment including outdated equipment. Many small donations ($1 to $5,000) are particularly important to maintaining tax exempt status with the IRS.

The Foundation is committed to complying with the laws regulating charities and charitable donations in all 50 states of the United States. Compliance requirements are not uniform and it takes a considerable effort, much paperwork and many fees to meet and keep up with these requirements. We do not solicit donations in locations where we have not received written confirmation of compliance. To SEND DONATIONS or determine the status of compliance for any particular state visit www.gutenberg.org/donate.

While we cannot and do not solicit contributions from states where we have not met the solicitation requirements, we know of no prohibition against accepting unsolicited donations from donors in such states who approach us with offers to donate.

International donations are gratefully accepted, but we cannot make any statements concerning tax treatment of donations received from outside the United States. U.S. laws alone swamp our small staff.

Please check the Project Gutenberg web pages for current donation methods and addresses. Donations are accepted in a number of other ways including checks, online payments and credit card donations. To donate, please visit: www.gutenberg.org/donate.

Section 5. General Information About Project Gutenberg™ electronic works

Professor Michael S. Hart was the originator of the Project Gutenberg™ concept of a library of electronic works that could be freely shared with anyone. For forty years, he produced and distributed Project Gutenberg™ eBooks with only a loose network of volunteer support.

Project Gutenberg™ eBooks are often created from several printed editions, all of which are confirmed as not protected by copyright in the U.S. unless a copyright notice is included. Thus, we do not necessarily keep eBooks in compliance with any particular paper edition.

Most people start at our website which has the main PG search facility: www.gutenberg.org.

This website includes information about Project Gutenberg™, including how to make donations to the Project Gutenberg Literary Archive Foundation, how to help produce our new eBooks, and how to subscribe to our email newsletter to hear about new eBooks.

		Seite
	Vorwort	III–VI
I. Geometrische Begriffe.
§ 1.	Senkrechte, wagrechte, schräge und parallele Linien	1
§ 2.	Winkel; rechte, stumpfe und spize	1–3
§ 3.	Dreiecke; gleichseitige, gleichschenklige, rechtwinklige	3–4
§ 4.	Vierecke; Quadrat, Rechteck, Raute, Trapez	4–5
§ 5.	Der Kreis. Hilfsmittel zum perspectivischen Zeichnen	5–6
II. Grundbegriffe der Perspective.
§ 6–11.	Unterschied der geometrischen und perspectivischen Form	7–14
§ 12–13.	Der Standpunkt; Sehkreis, Augpunkt, Horizont	15–19
§ 14–20.	Die Distanz	19–23
§ 21–24.	Das Grundgesez der perspectivischen Formerscheinung. Verkürzte und unverkürzte Stellung der Flächen und Linien	24–27
III. Perspectivische Richtung verkürzter Linien.
§ 25–27.	Verkürzte Parallellinien	28–31
§ 28–31.	Verkürzte wagrechte Linien	31–37
§ 32–36.	Rechtwinklige wagrechte Linien	37–45
§ 37.	Verkürzte wagrechte Linien, deren Richtung nicht genau zu berechnen ist	45
§ 38–40.	Wagrechte Parallellinien, deren Fluchtpunkt unzugänglich ist	46–51
§ 41–44.	Verkürzte schräge Linien	51–57
§ 45–48.	Berechnung der Richtung schräger Linien ohne Hilfe ihrer Fluchtpunkte	57–62
§ 49–61.	Verschiedene Beispiele: Treppen, Dächer, Dachfenster, Turmhelme	62–80
IV. Die perspectivischen Grössenverhältnisse. [VIII]
§ 62.	Unterscheidung der verschiedenen Aufgaben	81
§ 63–70.	Parallellinien von gleicher Länge in verschiedener Tiefe	82–90
§ 71–73.	Teilung einer verkürzten Linie nach bestimmten Verhältnissen	90–94
§ 74–79.	Perspectivisches Grössenverhältnis nicht paralleler Linien	95–105
§ 80.	Das Quadrat in gerader Stellung	105–106
§ 81–85.	Das Quadrat in schräger Stellung	106–111
§ 86–87.	Vergrösserung oder Verkleinerung eines Quadrats oder Rechtecks	111–115
V. Verkürzte Kreise, Achtecke und Sechsecke; Gewölbeformen.
§ 88–90.	Der Kreis in verkürzter Stellung	116–119
§ 91.	Parallele und concentrische Kreise	119–120
§ 92.	Teilung eines verkürzten Kreises	120–121
§ 93–95.	Verkürzte Achtecke	122–127
§ 96–98.	Verkürzte Sechsecke	127–130
§ 99–100.	Weitere Beispiele: Rad, Wasserrad, Walze, Cylinder	130–133
§ 101–108.	Tonnengewölbe, Kreuzgewölbe, Spizbogen, Kuppel	133–144