Transcriber’s Note:
The cover image was created by the transcriber and is placed in the public domain.
International Scientific Series
VOLUME XCVIII.
DIRECT REPRODUCTIONS OF AUTOCHROME PHOTOGRAPHS OF SCREEN PICTURES IN POLARISED LIGHT.

Fig. 90.—Screen Picture in Polarised Light, with Nicols crossed, of a thick Plate perpendicular to the Axis of a naturally twinned Crystal of Quartz, the left half being of right-handed Quartz and the right half of alternately left and right-handed Quartz, the Planes of Demarcation being oblique to the Plate.

Fig. 97.—Crystals of Benzoic Acid in the Act of Growth, as seen on the Screen in Polarised Light with crossed Nicols.
The International Scientific Series
CRYSTALS
BY
A. E. H. TUTTON
D.Sc., M.A. (New College, Oxon.), F.R.S.
VICE-PRESIDENT OF THE MINERALOGICAL SOCIETY MEMBER OF THE COUNCILS OF THE CHEMICAL SOCIETY AND THE BRITISH ASSOCIATION FOR THE ADVANCEMENT OF SCIENCE
WITH 120 ILLUSTRATIONS
LONDON
KEGAN PAUL, TRENCH, TRÜBNER & CO. LTD
DRYDEN HOUSE, GERRARD STREET, W.
1911
v
PREFACE
The idea underlying this book has been to present
the phenomena of crystallography to the general
reading public in a manner which can be comprehended
by all. In the main the sequence is that
of the author’s evening discourse to the British
Association at their meeting at Winnipeg in the
summer of 1909. It is hoped, however, that the
book combines the advantages of sufficient amplification
of the story there told to make it an
adequately detailed account of the development
of the subject, and of the immense progress which
has been made in it during recent years, with a full
description of the numerous experimental illustrations
given in the lecture, involving some of the
most beautiful phenomena displayed by crystals
in polarised light. Such an account has not been
otherwise published, the brief abstract appearing
in the Report of the British Association for 1909
giving no account of the experiments, which were
a feature of the lecture, owing to the employment
of a fine projection polariscope of more or less novel
construction, and including two magnificent large
Nicol prisms, a pair of the original ones made by
Ahrens. The author has been frequently requested
to publish a fuller account of this discourse, and as
the general plan of it so fully embodies the present
aspect of this fascinating science, it was determined,
viwhen invited by the publishers to write a generally
readable book on “Crystals,” to comply with these
requests.
There is also included an account of the remarkable
work of Lehmann and his fellow workers on “Liquid
Crystals,” and the bearing of these discoveries on
the nature of crystal structure is discussed in so far
as the experimental evidence has gone. Similarly,
the theory of Pope and Barlow, connecting crystalline
structure with the chemical property of valency,
is referred to and explained, as this theory has called
forth deep and widespread interest. In both cases,
however, the author has been careful to avoid any
expression of opinion on purely theoretical questions
for which there is as yet no definite experimental
evidence, and has confined himself strictly to indicating
how far such interesting theories are
supported by actual experimental facts.
No forbidding mathematical formulæ and no
unessential technical terms will be found in the book,
the aim of the author being to make any ordinarily
cultured reader feel at the conclusion that the story
has been readily comprehensible, and that crystallography
is not the abstruse and excessively difficult
subject which it has so generally been supposed to
be, but that, on the contrary, it is both simple and
straightforward, and full of the most enthralling
interest, as well for the exquisite phenomena with
which it deals, as for the exceedingly important
bearing which it has on the nature, both chemical
and physical, of solid matter.
If any of its readers should be so impressed with
the value of work in this domain of science as to be
viidesirous of joining the very thin ranks of the few who
are engaged in it, they will find a guide to practical
goniometry and to the experimental investigation
of crystals in all its branches and details, as well as
the necessary theoretical help, in the author’s book
on “Crystallography and Practical Crystal Measurement”
(Macmillan & Co., 1911), and also an account
of the author’s own contributions to the subject
in a monograph entitled “Crystalline Structure and
Chemical Constitution” (Macmillan & Co., 1910).
January 1911.
ix
CONTENTS
|
|
PAGE |
| Preface |
v |
| CHAPTER |
|
|
| I. |
Introduction |
1 |
| II. |
The Masking of Similarity of Symmetry and Constancy of Angle by Difference of Habit, and its Influence on Early Studies of Crystals |
10 |
| III. |
The prescient Work of the Abbé Haüy |
22 |
| IV. |
The Seven Styles of Crystal Architecture |
33 |
| V. |
How Crystals are Described. The Simple Law limiting the Number of possible Forms |
50 |
| VI. |
The Distribution of Crystal Faces in Zones, and the Mode of Constructing a Plan of the Faces |
60 |
| VII. |
The Work of Eilhardt Mitscherlich and his Discovery of Isomorphism |
70 |
| VIII. |
Morphotropy as distinct from Isomorphism |
98 |
| IX. |
The Crystal Space-Lattice and its Molecular Unit Cell. The 230 Point-Systems of Homogeneous Crystal Structure |
111 |
| X. |
Law of Variation of Angles in Isomorphous Series. Relative Dimensions of Unit Cells. Fixity of Atoms in Crystal |
121 |
| xXI. |
The Explanation of Polymorphism and the Relation between Enantiomorphism and Optical Activity |
133 |
| XII. |
Effect of the Symmetry of Crystals on the Passage of Light through them. Quartz, Calcite, and Gypsum as Examples |
162 |
| XIII. |
Experiments in Convergent Polarised Light with Quartz, as an Example of Mirror-Image Symmetry and its accompanying Optical Activity |
183 |
| XIV. |
Experiments with Quartz and Gypsum in Parallel Polarised Light. General Conclusions from the Experiments with Quartz |
201 |
| XV. |
How a Crystal Grows from a Solution |
236 |
| XVI. |
Liquid Crystals |
255 |
| XVII. |
The Chemical Significance of Crystallography. The Theory of Pope and Barlow—Conclusion |
283 |
| Index |
295 |
CRYSTALS
(INCLUDING LIQUID CRYSTALS)
1
CHAPTER I
INTRODUCTION.
It is a remarkable fact that no definition of life
has yet been advanced which will not apply to a
crystal with as much veracity as to those obviously
animate objects of the animal and vegetable world
which we are accustomed to regard in the ordinary
sense as “living.” A crystal grows when surrounded
by a suitable environment, capable of
supporting it with its natural food, namely, its own
chemical substance in the liquid or vaporous state
or dissolved in a solvent. Moreover, when a crystal
is broken, and then surrounded with this proper
environment, it grows much more rapidly at the
broken part than elsewhere, repairing the damage
done in a very short space of time and soon presenting
the appearance of a perfect crystal once
more. In this respect it is quite comparable with
animal tissue, the wonderful recuperative power
of which after injury, exhibited by special growth
at the injured spot, is often a source of such marvel
to us. Indeed, a crystal may be broken in half,
and yet each half in a relatively very brief interval
2will grow into a crystal as large as the original
one again. The longevity and virility of the spores
and seeds of the vegetable kingdom have been the
themes of frequent amazement, although many of
the stories told of them have been unable to stand
the test of strict investigation. The virility of a
crystal, however, is unchanged and permanent.
A crystal of quartz, rock-crystal, for instance—detached,
during the course of the disintegration
of the granitic rock of which it had originally formed
an individual crystal, by the denuding influences
at work in nature thousands of years ago, subsequently
knocked about the world as a rounded
sand grain, blown over deserts by the wind, its
corners rounded off by rude contact with its fellows,
and subjected to every variety of rough treatment—may
eventually in our own day find itself in water
containing in solution a small amount of the material
of which quartz is composed, silicon dioxide SiO2.
No sooner is this favourable environment for continuing
its crystallisation presented to it, than, however
old it may be, it begins to sprout and grow again.
It becomes surrounded in all probability by a beautiful
coating of transparent quartz, with exterior faces
inclined at the exact angles of quartz, although no
sign of exterior faces had hitherto persisted through
all the stages of its varied adventures. Or it may
grow chiefly at two or three especially favourable
places, and in the course of a few weeks, under suitable
conditions, at each place a perfect little quartz
crystal will radiate out from the sand grain, composed
of a miniature hexagonal prism terminated by the
well-known pyramid, really consisting of a pair of
3trigonal (rhombohedral) pyramids more or less equally
developed, and together producing an apparently
hexagonal one. Four such grains of sand, from
which quartz crystals are growing, are shown in
Fig. 1, as they appear under a microscope magnifying
about fifty diameters. One of them shows
a perfectly developed doubly terminated crystal of
quartz growing from the tip of a singly terminated
one, attached to and growing directly out of the
grain.

Fig. 1.—Sand Grains with Quartz Crystals growing from them.
This marvellously everlasting power possessed
by a crystal, of silent imperceptible growth, that
is, of adding to its own regular structure further
accretions of infinitesimal particles, the chemical
molecules, of its own substance, is one of the strangest
4functions of solid matter, and one of the fundamental
facts of science which is rarely realised, compared
with many of the more obvious phenomena of
nature.
A crystal in the ordinary sense of the word is
solid matter in its most perfectly developed and
organised form. It is composed of the chemical
molecules of some definitely constituted substance,
which have been laid down in orderly sequence,
in accordance with a specific architectural plan
peculiar to that particular chemical substance.
The physical properties of the latter are such that
it assumes the solid form at the ordinary temperature
and pressure, leaving out of consideration for the
present the remarkable viscous and liquid substances
which will be specially dealt with in Chapter
XVI. of this book, and which are currently known
as “liquid crystals.” This term is not perhaps a
very appropriate one. For the word “crystal”
had much better be left to convey the idea of rigidity
of polyhedral form and internal structure, which is
the very basis of crystal measurement.
The solid crystal may have been produced during
the simple act of congealment from the liquid state,
on the cooling of the heated liquefied substance
to the ordinary temperature. Sulphur, for instance,
is well-known to crystallise in acicular crystals
belonging to the monoclinic system under such conditions,
a characteristic crop being shown in Fig. 2
(Plate I.); they were formed within an earthenware
crucible in which the fusion had occurred, and
became revealed on pouring out the remainder
of the liquid sulphur when the crystallisation had
proceeded through about one-half of the original
amount of the “melt.”

PLATE I.
Fig. 2.—Monoclinic Acicular Crystals of Sulphur produced by Solidification of Liquid.
Fig. 3.—Octahedral Crystals of Arsenious Oxide produced by Condensation of Vapour.
Crystals formed by Different Processes.
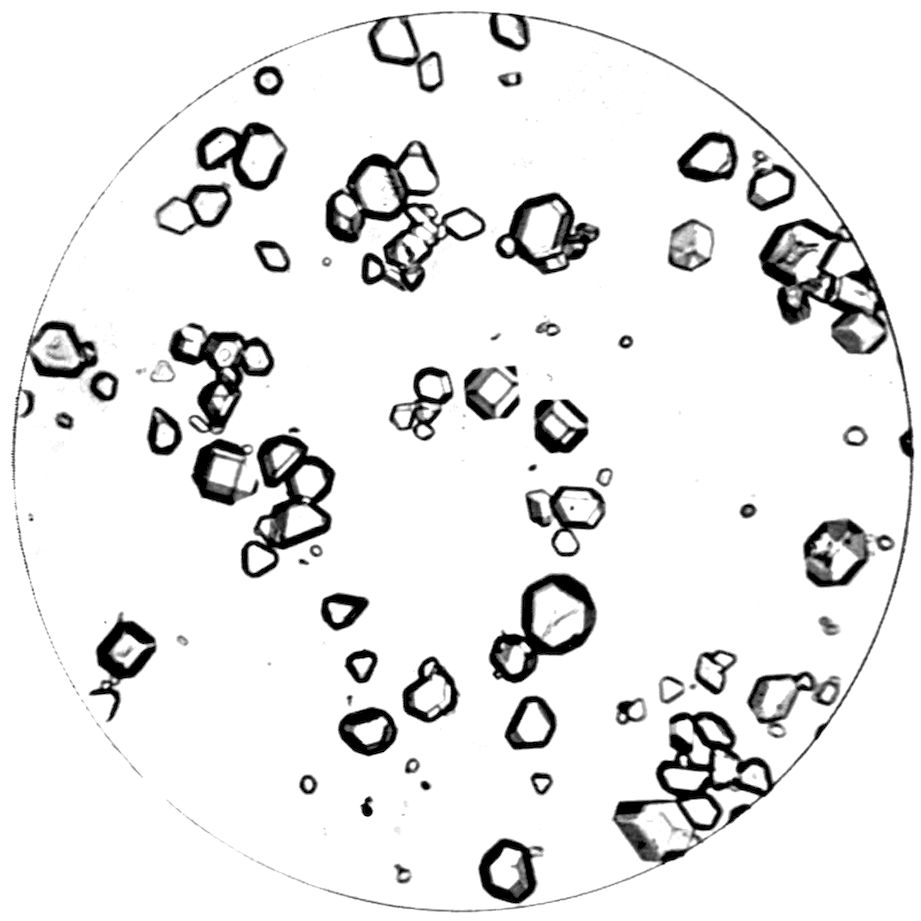
PLATE II.
Fig. 4.—Cubic Octahedral Crystals of Potash Alum growing from Solution.
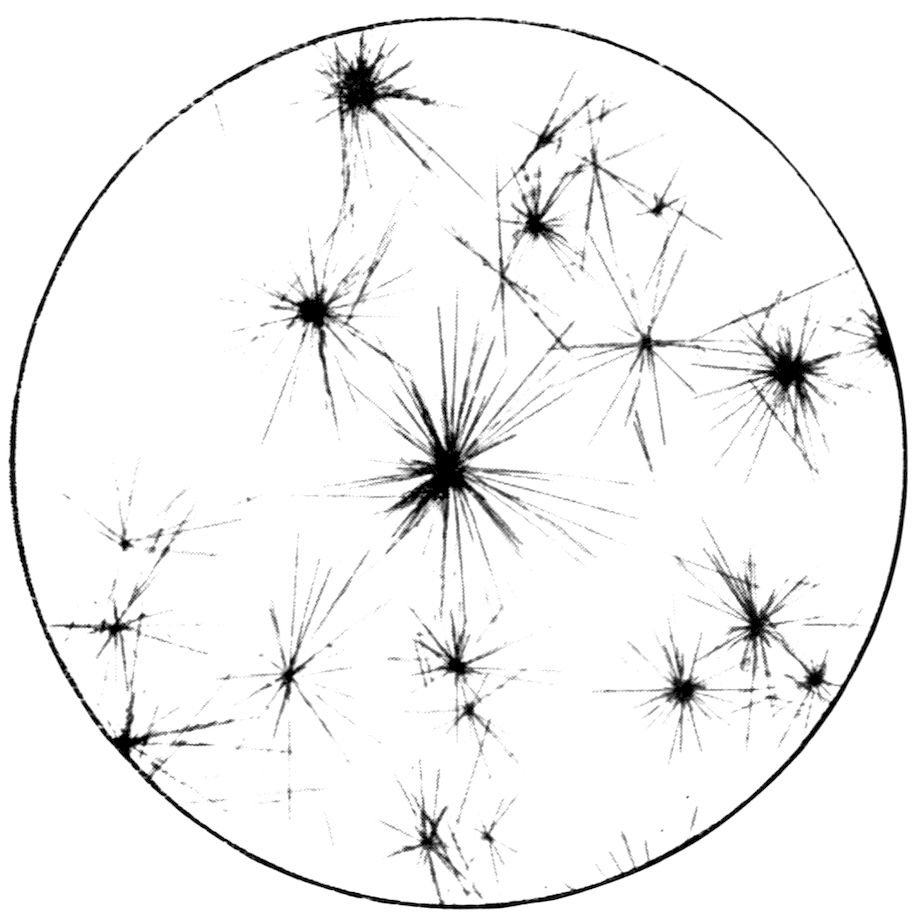
Fig. 10.—Micro-Chemical Crystals of Gypsum (Calcium Sulphate) produced by Slow Precipitation (see p. 14).
Crystals formed by Different Processes.
5Or the substance may be one which passes directly
from the gaseous to the solid condition, on the
cooling of the vapour from a temperature higher
than the ordinary down to the latter, under atmospheric
pressure. Oxide of arsenic, As2O3, is a
substance exhibiting this property characteristically,
and Fig. 3 (Plate I.) is a reproduction of a photograph
of crystals of this substance thus produced.
The white solid oxide was heated in a short test
tube over a Bunsen flame, and the vapour produced
was allowed to condense on a microscope glass
slip, and the result examined under the microscope,
using a 1½ inch objective. Fig. 3 represents
a characteristic field of the transparent octahedral
crystals.
Or again, the crystal may have been deposited
from the state of solution in a solvent, in which
case it is a question of the passage of the substance
from the liquid to the solid condition, complicated
by the presence of the molecules of the solvent,
from which the molecules of the crystallising solid
have to effect their escape. Fig. 4 (Plate II.) represents
crystals of potash alum, for instance, growing
from a drop of saturated solution on a glass slip
placed on the stage of the microscope, the drop
being spread within a hard ring of gold size and under
a cover-glass, in order to prevent rapid evaporation
and avoid apparent distortion by the curvature of an
uncovered drop. The crystals are of octahedral habit
like those of oxide of arsenic, but many of them also
exhibit the faces of the cube.
6In any case, however it may be erected, the
crystal edifice is produced by the regular accretion
of molecule on molecule, like the bricks or stone
blocks of the builder, and in accordance with an
architectural plan more elaborate and exact than
that of any human architect. This plan is that of
one of the thirty-two classes into which crystals
can be naturally divided with respect to their
symmetry. Which specific one is developed, and
its angular dimensions, are traits characteristic of
the substance. The thirty-two classes of crystals
may be grouped in seven distinctive systems,
the seven styles of crystal architecture, each distinguished
by its own elements of symmetry.
A crystal possesses two further fundamental
properties besides its style of architecture. The
first is that it is bounded externally by plane faces,
arranged on the definite geometrical plan just alluded
to and mutually inclined at angles which are peculiar
to the substance, and which are, therefore, absolutely
constant for the same temperature and
pressure. The second is that a crystal is essentially
a homogeneous solid, its internal structure being
similar throughout, in such wise that the arrangement
about any one molecule is the same as about
every other. This structure is, in fact, that of
one of the 230 homogeneous structures ascertained
by geometricians to be possible to crystals with
plane faces. The first property, that of the planeness
of the crystal faces, and their arrangement
with geometrical symmetry, is actually determined
by the second, that of specific homogeneity. For,
as with human nature developed to its highest
7type, the external appearance is but the expression
of the internal character.
When nature has been permitted to have fair
play, and the crystal has been deposited under
ideal conditions, the planeness of its faces is astonishingly
absolute. It is fully equal to that attained
by the most skilled opticians after weeks of
patient labour, in the production of surfaces on
glass or other materials suitable for such delicate
optical experiments as interference-band production,
in which a distortion equal to one wave-length of
light would be fatal. In all such cases of ideal
deposition, those interfacial angles on the crystal
which the particular symmetry developed requires
to be equal actually are so, to this same high degree
of refinement. This fact renders possible exceedingly
accurate crystal measurement, that is, the determination
of the angles of inclination of the faces to
each other, provided refined measuring instruments
(goniometers), pure chemical substances, and the
means of avoiding disturbance, either material
or thermal, during the deposition of the crystal,
are available.
The study of crystals naturally divides itself
into two more or less distinct but mutually very
helpful branches, and equally intimately connected
with the internal structure of crystals, namely,
one which concerns their exterior configuration
and the structural morphology of which it is the
eloquent visible expression, and another which relates
to their optical characters. For the latter
are so definitely different for the different systems
of crystal symmetry that they afford the greatest
8possible help in determining the former, and give
the casting vote in all cases of doubt left after
the morphological investigation with the goniometer.
It is, of course, their brilliant reflection
and refraction of light, with production of numerous
scintillations of reflected white light and of refracted
coloured spectra, which endows the hard and
transparent mineral crystals, known from time
immemorial as gem-stones, with their attractive
beauty. Indeed, their outer natural faces are
frequently, and unfortunately usually, cut away
most sacrilegiously by the lapidary, in order that by
grinding and polishing on them still more numerous
and evenly distributed facets he may increase to the
maximum the magnificent play of coloured light
with which they sparkle.
An interesting and very beautiful lecture experiment
was performed by the author in a lecture
a few years ago at the Royal Institution, which
illustrated in a striking manner this fact that the
light reaching the eye from a crystal is of two kinds,
namely, white light reflected from the exterior
faces and coloured light which has penetrated the
crystal substance and emerges refracted and dispersed
as spectra. Two powerful beams of light
from a pair of widely separated electric lanterns
were concentrated on a cluster of magnificent
large diamonds, kindly lent for the purpose by
Mr Edwin Streeter, and arranged in the shape of
a crown, it being about the time of the Coronation
of His late Majesty King Edward VII. The effect
was not only to produce a blaze of colour about the
diamonds themselves, but also to project upon the
9ceiling of the lecture theatre numerous images in
white light of the poles of the electric arc, derived
by reflection from the facets, interspersed with
equally numerous coloured spectra derived from
rays which had penetrated the substance of the
diamonds, and had suffered both refraction and
internal reflection.
10
CHAPTER II
THE MASKING OF SIMILARITY OF SYMMETRY AND CONSTANCY OF ANGLE BY DIFFERENCE OF HABIT, AND ITS INFLUENCE ON EARLY STUDIES OF CRYSTALS.
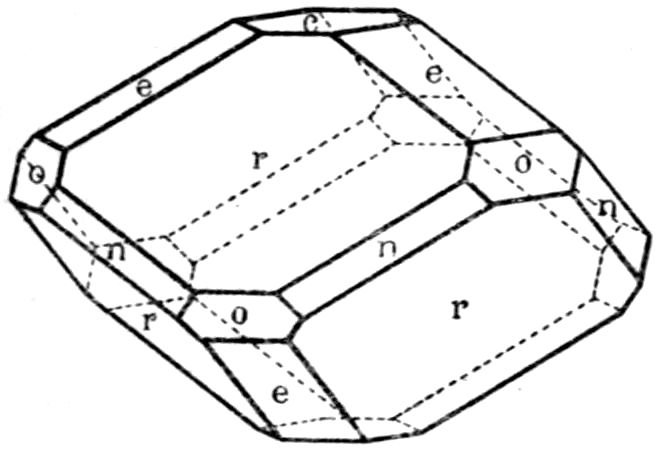
Fig. 5.—Natural Rhombohedron of Iceland Spar with Subsidiary Faces.
Nothing is more remarkable than the great variety
of geometrical shapes which the crystals of the
same substance, derived from different localities or
produced under different
conditions, are observed
to display. One of the
commonest of minerals,
calcite, carbonate of lime,
shows this feature admirably;
the beautiful large
rhombohedra from Iceland,
illustrated in Fig. 5,
or the hexagonal prisms
capped by low rhombohedra from the Bigrigg mine
at Egremont in Cumberland, shown in Fig. 6, appear
totally different from the “dog-tooth spar” so plentifully
found all over the world, a specimen of which
from the same mine is illustrated in Fig. 7. No
mineral specimens could well appear more dissimilar
than these represented on Plate III. in Figs. 6 and 7,
when seen side by side in the mineral gallery of the
British Museum (Natural History) at South Kensington. But all are composed of similar chemical
molecules of calcium carbonate, CaCO3; and when
the three kinds of crystals are investigated they
are found to be identical in their crystalline system,
the trigonal, and indeed further as to the subdivision
or class of that system, which has come to be called
the calcite class from the importance of this mineral.

PLATE III.
Fig. 6.—Hexagonal Prisms of Calcite terminated by Rhombohedra.

Fig. 7.—Scalenohedral Crystals of Calcite, “Dog-tooth Spar.”
Crystals of Calcite from the same Mine, illustrating Diversity of Habit.
(Photographed from Specimens in the Natural History Department of the British Museum, by kind permission.)
11Moreover, many of the same faces, that is, faces
having the same relation to the symmetry, are
present on all three varieties, the “forms” to which
they equally belong being the common heritage of
calcite wherever found. A “form” is the technical
term for a set of faces having an equal value with
respect to the symmetry. Thus the prismatic
form in Fig. 6 is the hexagonal prism, a form which
is common to the hexagonal and trigonal systems
of symmetry, and the form “indices” (numbers[1]
inversely proportional to the intercepts cut off from
the crystal axes by the face typifying the form) of
which are {2̄1̄1}; the large development of this
form confers the elongated prismatic habit on the
crystal. The terminations are faces of the flat
rhombohedron {110}. The pyramidal form of
the dog-tooth spar shown in Fig. 7 is the scalenohedron
{20̄1}, and it is this form which confers
the tooth-like habit, so different from the hexagonal
prism, upon this variety of calcite. But many
specimens of dog-tooth spar, notably those from
Derbyshire, consist of scalenohedra the middle portion
of which is replaced by faces of the hexagonal prism
{2̄1̄1}, and the terminations of which are replaced by
12the characteristic rhombohedron {100} of Iceland
spar; indeed, it is quite common to find crystals of
calcite exhibiting on the same individual all the
forms which have been mentioned, that is, those
dominating the three very differently appearing
types. The author has quite recently measured such a
crystal, which, besides showing all these four forms
well developed, also exhibited the faces of two others
of the well-known forms of calcite, {3̄1̄1} and {310},
and a reproduction of a drawing of it to scale is
given in Fig. 8. Instead of indices the faces of
each form bear a distinctive letter; m = {2̄1̄1},
r = {100}, e = {110}, v = {20̄1}
(the faces of the scalenohedron
are of somewhat small dimensions
on this crystal), n = {3̄1̄1},
and t = {310}.

Fig. 8.—Measured Crystal of Calcite.
It is obviously then the
“habit” which is different in
the three types of calcite—Iceland
spar, prismatic calc-spar,
and dog-tooth spar—doubtless
owing to the different local circumstances
of growth of the
mineral. Habit is simply the
expression of the fact that a
specific “form,” or possibly two particular forms,
is or are much more prominently developed in
one variety than in another. Thus the principal
rhombohedron r = {100}, parallel to the faces
of which calcite cleaves so readily, is the predominating
form in Iceland spar, while the
13scalenohedron v = {20̄1} is the habit-conferring
form in dog-tooth spar. Yet on the latter the
rhombohedral faces are frequently developed,
blunting the sharp terminations of the scalenohedra,
especially in dog-tooth spar from Derbyshire or the
Hartz mountains; and on the former minute
faces of the scalenohedron are often found, provided
the rhombohedron consists of the natural exterior
faces of the crystal and not of cleavage faces. In
the same manner the prismatic crystals from Egremont
are characterised by two forms, the hexagonal
prism m = {2̄1̄1} and the secondary rhombohedron
e = {110}, but both of these forms, as we have seen
on the actual crystal represented in Fig. 8, are also
found developed on other crystals of mixed habit.
This illustration from the naturally occurring
minerals might readily be supplemented by almost
any common artificial chemical preparation, sulphate
of potash for instance, K2SO4, the orthorhombic
crystals of which take the form of elongated prisms,
even needles, on the one hand, or of tabular plate-like
crystals on the other hand, according as the
salt crystallises by the cooling of a supersaturated
solution, or by the slow evaporation of a solution
which at first is not quite saturated. In both
cases, and in all such cases, whether of minerals
or chemical preparations, the same planes are
present on the crystals of the same substance,
although all may not be developed on the same
individual except in a few cases of crystals particularly
rich in faces; and these same planes are
inclined at the same angles. But their relative
14development may be so very unlike on different
crystals as to confer habits so very dissimilar that
the fact of the identity of the substance is entirely
concealed.
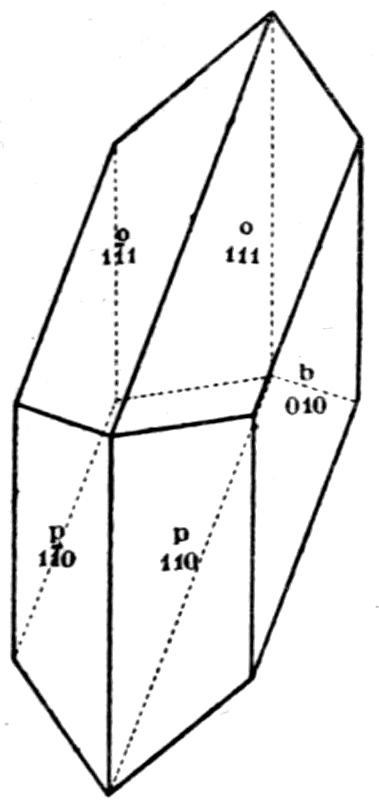
Fig. 9.—Crystal of Gypsum.
A further example may perhaps be given, that of a
substance, hydrated sulphate of lime, CaSO4.2H2O,
which occurs in nature as the beautiful transparent
mineral gypsum or selenite—illustrated in Fig. 9,
and which is found in monoclinic crystals often of
very large size—and which may also be chemically
prepared by adding a dilute solution of sulphuric
acid to a very dilute solution of calcium chloride.
The radiating groups of needles shown in Fig. 10
(Plate II.) slowly crystallise out when a drop of the
mixed solution is placed on a microscope
slip and examined under the
microscope, using the one-inch
objective. These needles, so absolutely
different in appearance from
a crystal of selenite, are yet similar
monoclinic prisms, but in which the
prismatic form is enormously elongated
compared with the other
(terminating) form.
This difference of facial development,
rendering the crystals of one
and the same substance from different
sources so very unlike each
other, was apparently responsible for the very tardy
discovery of the fundamental law of crystallography,
the constancy of the crystal angles of the same substance.
Gessner, sometime between the years 1560
15and 1568, went so far as to assert that not only are
different crystals of the same substance of different
sizes, but that also the mutual inclinations of their
faces and their whole external form are dissimilar.
What was much more obvious to the early
students of crystals, and which is, in fact, the most
striking thing about a crystal after its regular
geometric exterior shape, was the obviously homogeneous
character of its internal structure. So
many crystals are transparent, and so clear and
limpid, that it was evident to the earliest observers
that they were at least as homogeneous throughout as
glass, and yet that at the same time they must be
endowed with an internal structure the nature of
which is the cause of both the exterior geometric
regularity of form, so different from the irregular
shape of a lump of glass, and of the peculiar effect
on the rays of light which are transmitted through
them. From the earliest ages of former civilisations
the behaviour of crystals with regard to light has
been known to be different for the different varieties
of gem-stones.
About the year 1600 Cæsalpinus observed that
sugar, saltpetre, and alum, and also the sulphates
of copper, zinc and iron, known then as blue,
white and green vitriol respectively, separate from
their solutions in characteristic forms. Had he
not attributed this to the operation of an organic
force, in conformity with the curious opinion of
the times concerning crystals, he might have had
the credit of being the pioneer of crystallographers.
The first two real steps in crystallography, however,
16with which in our own historic times we are
acquainted, were taken in the seventeenth century
within four years of each other, one from the interior
structural and the other from the exterior geometrical
point of view. For in 1665 Robert Hooke
in this country made a study of alum, which he
appears to have obtained in good crystals, although
he was unacquainted with its true chemical composition.
He describes in his “Micrographia”
how he was able to imitate the varying habits of
the octahedral forms of alum crystals by building
piles of spherical musket bullets, and states that
all the various figures which he observed in the
many crystals which he examined could be produced
from two or three arrangements of globular
particles. It is clear that the homogeneous partitioning
of space in a crystal structure by similar
particles building up the crystal substance was in
Hooke’s mind, affording another testimony to the
remarkably prescient insight of our great countryman.
Four years later, in 1669, Nicolaus Steno carried
out in Florence some remarkable measurements,
considering the absence of proper instruments,
of the angles between the corresponding faces of
different specimens of rock-crystal (quartz, the
naturally occurring dioxide of silicon, concerning
which there will be much to say later in this book),
obtained from different localities, and published
a dissertation announcing that he found these
analogous angles all precisely the same.
In the year 1688 the subject was taken up systematically
17by Guglielmini, and in two memoirs of
this date and 1705 he extended Steno’s conclusions
as to the constancy of crystal angles in the case of
rock-crystal into a general law of nature. Moreover,
he began to speculate about the interior structure
of crystals, and, like Hooke, he took alum as his
text, and suggested that the ultimate particles
possessed plane faces, and were, in short, miniature
crystals. He further announced the constancy of
the cleavage directions, so that to Guglielmini must
be awarded the credit for having, at a time when
experimental methods of crystallographic investigation
were practically nil, discovered the fundamental
principles of crystallography.
The fact that a perfect cleavage is exhibited by
calcite had already been observed by Erasmus
Bartolinus in 1670, and in his “Experimenta
Crystalli Islandici” he gives a most interesting
account of the great discovery of immense clear
crystals of calcite which had just been made at
Eskifjördhr in Iceland, minutely describing both
their cleavage and their strong double refraction.
Huyghens in 1690 followed this up by investigating
some of these crystals of calcite still more closely,
and elaborated his laws of double refraction as the
result of his studies.
There now followed a century which was scarcely
productive of any further advance at all in our
real knowledge of crystals. It is true that Boyle
in 1691 showed that the rapidity with which a
solution cools influences the habit of the crystals
which are deposited from it. But neither Boyle,
18with all his well-known ability, so strikingly displayed
in his work on the connection between the
volume of a gas and the pressure to which it is subjected,
nor his lesser contemporaries Lemery and
Homberg, who produced and studied the crystals
of several series of salts of the same base with different
acids, appreciated the truth of the great fact
discovered by Guglielmini, that the same substance
always possesses the same crystalline form the angles
of which are constant. Even with the growth of
chemistry in the eighteenth century, the opinion
remained quite general that the crystals of the
same substance differ in the magnitude of their
angles as well as in the size of their faces.
We begin to perceive signs of progress again in
the year 1767, when Westfeld made the interesting
suggestion that calcite is built up of rhombohedral
particles, the miniature faces of which correspond to
the cleavage directions. This was followed in 1780
by a treatise “De formis crystallorum” by Bergmann
and Gahn of Upsala, in which Guglielmini’s
law of the constancy of the cleavage directions
was reasserted as a general one, and intimately
connected with the crystal structure. It was in
this year 1780 that the contact goniometer was
invented by Carangeot, assistant to Romé de l’Isle
in Paris, and it at once placed at the disposal of his
master a weapon of research far superior to any
possessed by previous observers.
19
Fig. 11.—Contact Goniometer as used by Romé de l’Isle.
In his “Crystallographie,” published in Paris
in 1783, Romé de l’Isle described a very large number
of naturally occurring mineral crystals, and after
measuring their angles with Carangeot’s goniometer
he constructed models of no less than 500 different
forms. Here we have work based upon sound
measurement, and consequently of an altogether
different and higher value than that which had
gone before. It was the knowledge that his master
desired to faithfully reproduce the small natural
crystals which he was investigating, on the larger
scale of a model, that led Carangeot to invent the
contact goniometer, and thus to make the first start
in the great subject of goniometry. The principle
of the contact goniometer remains to-day practically
as Carangeot left it, and although replaced for
refined work by the reflecting goniometer, it is
still useful when large mineral crystals have to be
dealt with. An illustration of a duplicate of the
original instrument is shown in Fig. 11, by the
kindness of Dr H. A. Miers. This duplicate was
20presented to Prof. Buckland by the Duke of
Buckingham in the year 1824, and is now in the
Oxford Museum.
From the time that measurement of an accurate
description was possible by means of the contact
goniometer, progress in crystallography became
rapid. Romé de l’Isle laid down the sound principle,
as the result of the angular measurements and the
comparison of his accurate models with one another,
that the various crystal shapes developed by the
same substance, artificial or natural, were all intimately
related, and derivable from a primitive
form, characteristic of the substance. He considered
that the great variety of form was due to
the development of secondary faces, other than
those of the primitive form. He thus connected
together the work of previous observers, consolidated
the principles laid down by Guglielmini by
measurements of real value, and threw out the
additional suggestion of a fundamental or primitive
form.
About the same time Werner was studying the
principal forms of different crystals of the same
substance. The idea of a fundamental form appears
to have struck him also, and he showed how such
a fundamental form may be modified by truncating,
bevelling, and replacing its faces by other derived
forms. His work, however, cannot possess the
value of that of Romé de l’Isle, as it was not based
on exact measurement, and most of all because
Werner appears to have again admitted the fallacy
that the same substance could, in the ordinary way,
21and not in the sense now termed polymorphism,
exhibit several different fundamental forms.
But a master mind was at hand destined
definitely to remove these doubts and to place the
new science on a firm basis. An account of how
this was achieved is well worthy of a separate
chapter.
22
CHAPTER III
THE PRESCIENT WORK OF THE ABBÉ HAÜY.
The important work of Romé de l’Isle had paved
the way for a further and still greater advance
which we owe to the University of Paris, for its
Professor of the Humanities, the Abbé Réné Just
Haüy, a name ever to be regarded with veneration
by crystallographers, took up the subject shortly
after Romé de l’Isle, and in 1782 laid most important
results before the French Academy, which were
subsequently, in 1784, published in a book, under
the auspices of the Academy, entitled “Essai
d’une Théorie sur la Structure des Crystaux.”
The author happens to possess, as the gift of a
kind friend, a copy of the original issue of this
highly interesting and now very rare work. It
contains a brief preface, dated the 26th November
1783, signed by the Marquis de Condorcet,
perpetual secretary to the Academy (who, in
1794, fell a victim to the French revolution), to
the effect that the Academy had expressed its
approval and authorised the publication “under its
privilege.”
The volume contains six excellent plates of a
large number of most careful drawings of crystals,
illustrating the derivation from the simple forms,
such as the cube, octahedron, dodecahedron,
23rhombohedron, and hexagonal prism, of the more
complicated forms by the symmetrical replacement
of edges and corners, together with the drawings
of many structural lattices. In the text, Haüy
shows clearly how all the varieties of crystal forms
are constructed according to a few simple types of
symmetry; for instance, that the cube, octahedron,
and dodecahedron all have the same high degree
of symmetry, and that the apparently very diverse
forms shown by one and the same substance are
all referable to one of these simple fundamental
or systematic forms. Moreover, Haüy clearly states
the laws which govern crystal symmetry, and
practically gives us the main lines of symmetry
of five of the seven systems as we now classify
them, the finishing touch having been supplied in
our own time by Victor von Lang.
Haüy further showed that difference of chemical
composition was accompanied by real difference
of crystalline form, and he entered deeply into
chemistry, so far as it was then understood, in order
to extend the scope of his observations. It must be
remembered that it was only nine years before,
in 1774, that Priestley had discovered oxygen, and
that Lavoisier had only just (in the same year as
Haüy’s paper was read to the Academy, 1782)
published his celebrated “Elements de Chimie”;
and further, that Lavoisier’s memoir “Reflexions
sur le Phlogistique” was actually published by the
Academy in the same year, 1783, as that in which
this book was written by Haüy. Moreover, it was
also in this same year, 1783, that Cavendish
discovered the compound nature of water.
24Considering, therefore, all these facts, it is truly
surprising that Haüy should have been able to have
laid so accurately the foundations of the science
of crystallography. That he undoubtedly did so,
thus securing to himself for all time the term which
is currently applied to him of “father of crystallography,”
is clearly apparent from a perusal of his
book and of his subsequent memoirs.
The above only represents a small portion of
Haüy’s achievements. For he discovered, besides,
the law of rational indices, the generalisation which
is at the root of crystallographic science, limiting,
as it does, the otherwise infinite number of possible
crystal forms to comparatively few, which alone
are found to be capable of existence as actual crystals.
The essence of this law, which will be fully explained
in Chapter V., is that the relative lengths intercepted
along the three principal axes of the crystal, by
the various faces other than those of the fundamental
form, the faces of which are parallel to the
axes, are expressed by the simplest unit integers,
1, 2, 3, or 4, the latter being rarely exceeded and
then only corresponding to very small and altogether
secondary faces.
This discovery impressed Haüy with the immense
influence which the structure of the crystal substance
exerts on the external form, and how, in fact, it
determines that form. For the observations were
only to be explained on the supposition that the
crystal was built up of structural units, which he
imagined to be miniature crystals shaped like the
fundamental form, and that the faces were dependent
on the step-like arrangement possible to
25the exterior of such an assemblage. This brought
him inevitably to the intimate relation which cleavage
must bear to such a structure, that it really determined
the shape of, and was the expression of
the nature of, the structural units. Thus, before
the conception of the atomic theory by Dalton,
whose first paper (read 23rd October 1803), was
published in the year 1803 in the Proceedings of
the Manchester Literary and Philosophical Society,
two years after the publication of Haüy’s last work
(his “Traité de Minéralogie,” Paris, 1801), Haüy
came to the conclusion that crystals were composed
of units which he termed “Molécules Intégrantes,”
each of which comprised the whole chemical compound,
a sort of gross chemical molecule. Moreover,
he went still further in his truly original
insight, for he actually suggested that the molécules
intégrantes were in turn composed of “Molécules
Elémentaires,” representing the simple matter of
the elementary substances composing the compound,
and hinted further that these elementary portions
had properly orientated positions within the molécules
intégrantes.
He thus not only nearly forestalled Dalton’s
atomic theory, but also our recent work on the
stereometric orientation of the atoms in the molecule
in a crystal structure. Dalton’s full theory
was not published until the year 1811, in his epoch-making
book entitled “A New System of Chemical
Philosophy,” although his first table of atomic
weights was given as an appendix to the memoir of
1803. Thus in the days when chemistry was in
the making at the hands of Priestley, Lavoisier,
26Cavendish, and Dalton do we find that crystallography
was so intimately connected with it that a
crystallographer well-nigh forestalled a chemist
in the first real epoch-making advance, a lesson
that the two subjects should never be separated
in their study, for if either the chemist or the crystallographer
knows but little of what the other is
doing, his work cannot possibly have the full value
with which it would otherwise be endowed.
The basis of Haüy’s conceptions was undoubtedly
cleavage. He describes most graphically on page
10 of his “Essai” of 1784 how he was led to make
the striking observation that a hexagonal prism of
calcite, terminated by a pair of hexagons normal to
the prism axis, similar to the prisms shown in Fig. 6
(Plate III.) except that the ends were flat, showed
oblique internal cleavage cracks, by enhancing which
with the aid of a few judicious blows he was able to
separate from the middle of the prism a kernel in
the shape of a rhombohedron, the now well-known
cleavage rhombohedron of calcite. He then tried
what kinds of kernels he could get from dog-tooth
spar (illustrated in Fig. 7) and other different forms
of calcite, and he was surprised to find that they
all yielded the same rhombohedral kernel. He
subsequently investigated the cleavage kernels of
other minerals, particularly of gypsum, fluorspar,
topaz, and garnet, and found that each mineral
yielded its own particular kernel. He next imagined
the kernels to become smaller and smaller, until
the particles thus obtained by cleaving the mineral
along its cleavage directions ad infinitum were the
smallest possible. These miniature kernels having
27the full composition of the mineral he terms “Molécules
Constituantes” in the 1784 “Essai,” but in the
1801 “Traité” he calls them “Molécules Intégrantes”
as above mentioned. He soon found that there
were three distinct types of molécules intégrantes,
tetrahedra, triangular prisms, and parallelepipeda,
and these he considered to be the crystallographic
structural units.
Having thus settled what were the units of the
crystal structure, Haüy adopted Romé de l’Isle’s
idea of a primitive form, not necessarily identical
with the molécule intégrante, but in general a
parallelepipedon formed by an association of a few
molécules intégrantes, the parallelepipedal group
being termed a “Molécule Soustractive.” The
primary faces of the crystal he then supposed to
be produced by the simple regular growth or piling
on of molécules intégrantes or soustractives on the
primitive form. The secondary faces not parallel
to the cleavage planes next attracted his attention,
and these, after prolonged study, he explained
by supposing that the growth upon the primitive
form eventually ceased to be complete at the edges
of the primary faces, and that such cessation occurred
in a regular step by step manner, by the suppression
of either one, two, or sometimes three molécules
intégrantes or soustractives along the edge of each
layer, like a stepped pyramid, the inclination of
which depends on how many bricks or stone blocks
are intermitted in each layer of brickwork or masonry.
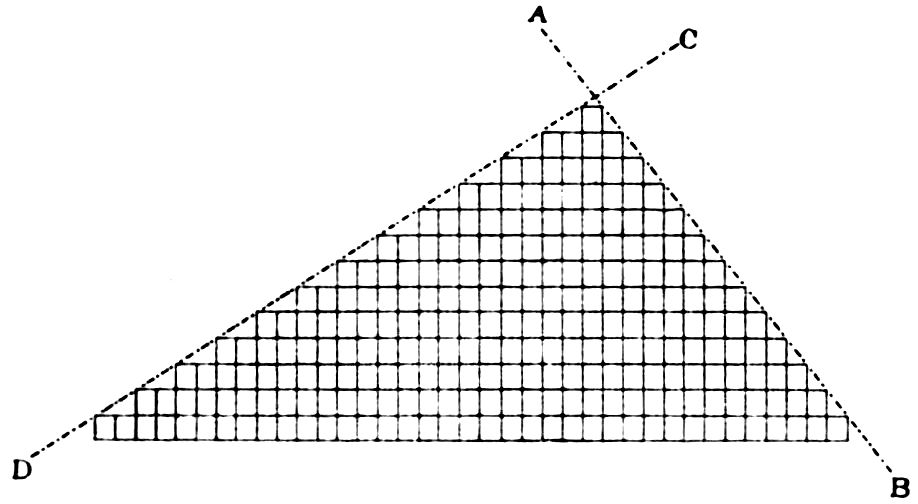
Fig. 12 will render this quite clear, the face AB
being formed by single block-steps, and the face
CD by two blocks being intermitted to form each
28step. The plane AB or CD containing the outcropping
edges of the steps would thus be the
secondary plane face of the crystal, and the molécules
intégrantes or soustractives (the steps can only be
formed by parallelepipedal units) being infinitesimally
small, the re-entrant angles of the steps
would be invisible and the really furrowed surface
appear as a plane one. Haüy is careful to point
out, however, that the crystallising force which
causes this stepped development (or lack of development)
is operative
from the
first, for the
minutest crystals
show secondary
faces, and often
better than the
larger crystals.
An instance of
a mineral with
tetrahedral molécules intégrantes Haüy gives in tourmaline,
and the primitive form of tourmaline he considered
to be a rhombohedron, conformably to the
well-known rhombohedral cleavage of the mineral,
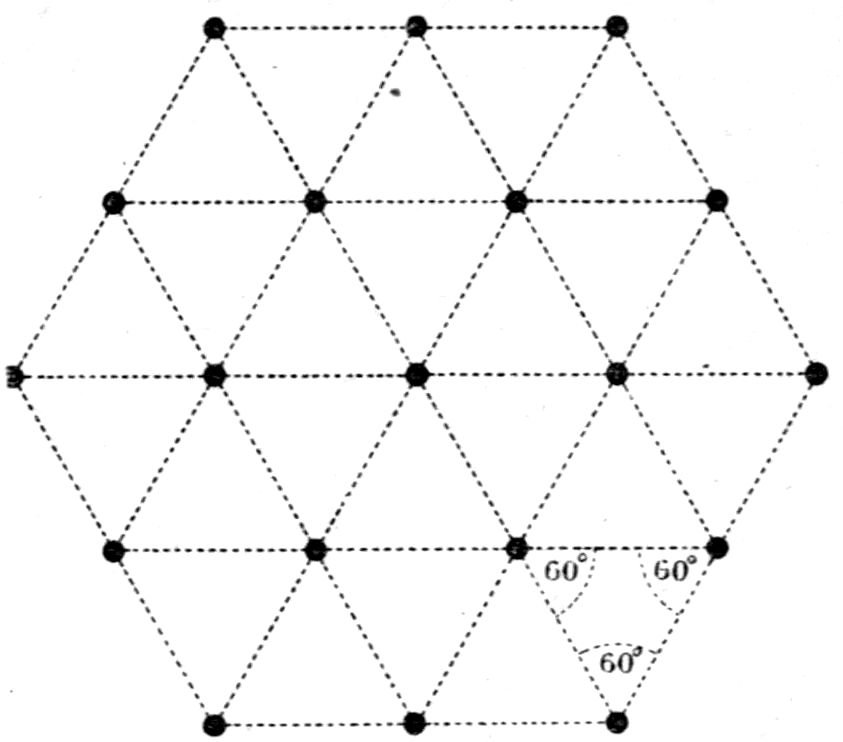
made up of six tetrahedra. Again, hexagonal
structures formed by three prismatic cleavage planes
inclined at 60° are considered by him as being
composed of molécules intégrantes of the form of 60°
triangular prisms, or molécules soustractives of the
shape of 120° rhombic prisms, each of the latter being
formed by two molécules intégrantes situated base to
base. This will be clear from Figs. 13 and 14, the
former representing the structure as made up of
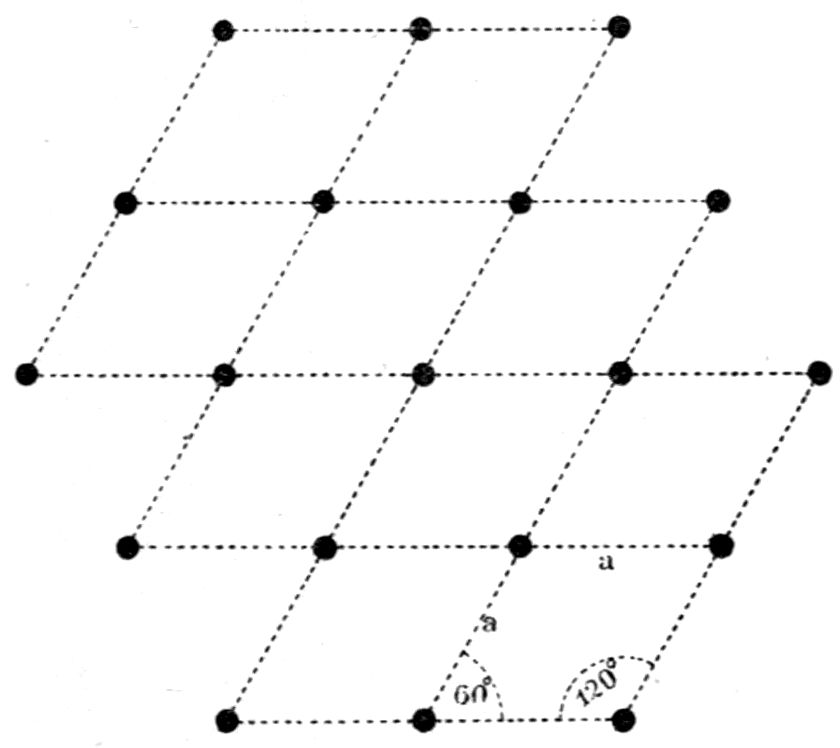
29equilateral prismatic structural units, and the latter
portraying the same structure but composed of 120°-parallelepipeda
by
elimination of one
cleavage direction;
each unit in the
latter case possesses
double the
volume of the
triangular one, and
being of parallelepipedal
section is
capable of producing
secondary faces
when arranged
step-wise, whereas the triangular structure is not.
The points at the intersections in these diagrams
should for the present be disregarded; they will
shortly be referred
to for another purpose.
Probably, the
most permanent
and important of
Haüy’s achievements
was the
discovery of the
law of rational
indices. At first
this only took the
form of the observation
of the very limited number of rows of
molécules intégrantes or soustractives suppressed.
30In introducing it on page 74 of his 1784 “Essai”
he says: “Quoique je n’aie observé jusqu’ici que
des décroissemens qui se sont par des soutractions
d’une ou de deux rangées de molécules, et quelquefois
de trois rangées, mais très rarement, il est possible
qu’il se trouve des crystaux dans lesquels il y ait
quatre ou cinq rangées de molécules supprimées à
chaque décroissement, et même un plus grand nombre
encore. Mais ces cas me semblent devoir être plus
rares, à proportion que le nombre des rangées soutraites
sera plus considérable. On conçoit donc comment
le nombre des formes secondaires est néçessairement
limité.”
The essential difference between Haüy’s views
and our present ones, which will be explained in
Chapter IX., is that Haüy takes cleavage absolutely
as his guide, and considers the particles, into which
the ultimate operation of cleavage divides a crystal,
as the solid structural units of the crystal, the unit
thus having the shape of at least the molécule
intégrante. Now every crystalline substance does
not develop cleavage, and others only develop
it along a single plane, or along a couple of planes
parallel to the same direction, that of their intersection
and of the axis of the prism which two such cleavages
would produce, and which prism would be of unlimited
length, being unclosed.
Again, in other cases cleavage, such as the octahedral
cleavage of fluorspar, yields octahedral
or tetrahedral molécules intégrantes which are not
congruent, that is to say, do not fit closely together
to fill space, as is the essence of Haüy’s theory.
Hence, speaking generally, partitioning by means
31of cleavage directions does not essentially and
invariably yield identical plane-faced molecules
which fit together in contact to completely fill
space, although in the particular instances chosen
from familiar substances by Haüy it often happens
to do so. Haüy’s theory is thus not adequately
general, and the advance of our knowledge of
crystal forms has rendered it more and more
apparent that Haüy’s theory was quite insufficient,
and his molécules intégrantes and soustractives mere
geometrical abstractions, having no actual basis
in material fact; but that at the same time it gave
us a most valuable indication of where to look for
the true conception.
This will be developed further into our present
theory of the homogeneous partitioning of space,
in Chapter IX. But it may be stated here, in
concluding our review of the pioneer work of Haüy,
that in the modern theory all consideration of the
shape of the ultimate structural units is abandoned
as unnecessary and misleading, and that each
chemical molecule is considered to be represented
by a point, which may be either its centre of gravity,
a particular atom in the molecule (for we are now
able in certain cases to locate the orientation of
the spheres of influence of the elementary atoms
in the chemical molecules), or a purely representative
point standing for the molecule. The only condition
is that the points chosen within the molecules
shall be strictly analogous, and similarly orientated.
The dots at the intersections of the lines in Figs.
13 and 14 are the representative points in question.
We then deal with the distances between the points,
32the latter being regarded as molecular centres,
rather than with the dimensions of the cells themselves
regarded as solid entities. We thus avoid
the as yet unsolved question of how much is matter
and how much is interspace in the room between
the molecular centres. In this form the theory
is in conformity with all the advances of modern
physics, as well as of chemistry. And with this
reservation, and after modifying his theory to this
extent, one cannot but be struck with the wonderful
perspicacity of Haüy, for he appears to have observed
and considered almost every problem with which
the crystallographer is confronted, and his laws
of symmetry and of rational indices are perfectly
applicable to the theory as thus modernised.
33
CHAPTER IV
THE SEVEN STYLES OF CRYSTAL ARCHITECTURE.
It is truly curious how frequently the perfect number,
seven, is endowed with exceptional importance with
regard to natural phenomena. The seven orders of
spectra, the seven notes of the musical octave, and
the seven chemical elements, together with the seven
vertical groups to which by their periodic repetition
they give rise, of the “period” of Mendeléeff’s classification
of the elements, will at once come to mind
as cases in point. This proverbial importance of
the number seven is once again illustrated in regard
to the systems of symmetry or styles of architecture
displayed by crystals. For there are seven
such systems of crystal symmetry, each distinguished
by its own specific elements of symmetry.
It is only within recent years that we have
come to appreciate what are the real elements
of symmetry. For although there are but
seven systems, there are no less than thirty-two
classes of crystals, and these were formerly
grouped under six systems, on lines which have
since proved to be purely arbitrary and not founded
on any truly scientific basis. It was supposed that
those classes in any system which did not exhibit
all the faces possible to the system owed this lack
of development to the suppression of one-half or
34three-quarters of the possible number, and such
classes were consequently called “hemihedral”
and “tetartohedral” respectively. As in the
higher systems of symmetry there were usually
two or more ways in which a particular proportionate
suppression of faces could occur, it happened that
several classes, and not merely three—holohedral
(possessing the full number of faces), hemihedral,
and tetartohedral—constituted each of these systems.
Thanks largely to the genius of Victor von Lang,
who was formerly with us in England at the Mineral
Department of the British Museum, and to his
successor there, Nevil Story Maskelyne, we have
at last a much more scientific basis for our classification
of crystals, and one which is in complete
harmony with the now perfected theory of possible
homogeneous structures. Victor von Lang showed
that the true elements of symmetry are planes of
symmetry and axes of symmetry. A crystal
possessing a plane of symmetry is symmetrical on
both sides of that plane, both as regards the number
of the faces and their precise angular disposition
with respect to one another.
It is quite possible, and even the usual case, that
the relative development of the faces, that is their
actual sizes, may prevent the symmetry from being
at first apparent; but when we come to measure
the angles between the faces, by use of the reflecting
goniometer, and to plot their positions out on the
surface of a sphere, or on a plane representation
of the latter on paper, the exceedingly useful
“stereographic projection,” we at once perceive
the symmetry perfectly plainly.
35
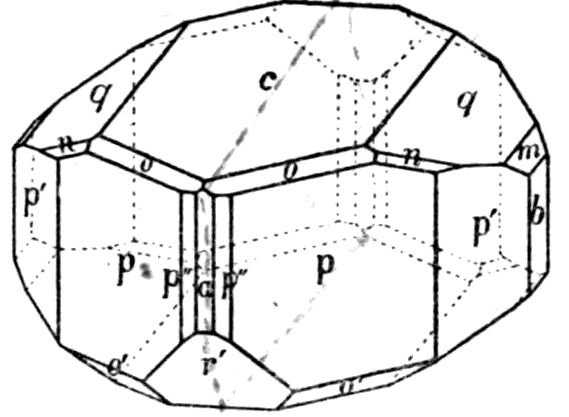
Fig. 15.—Crystal of Potassium Nickel Sulphate.
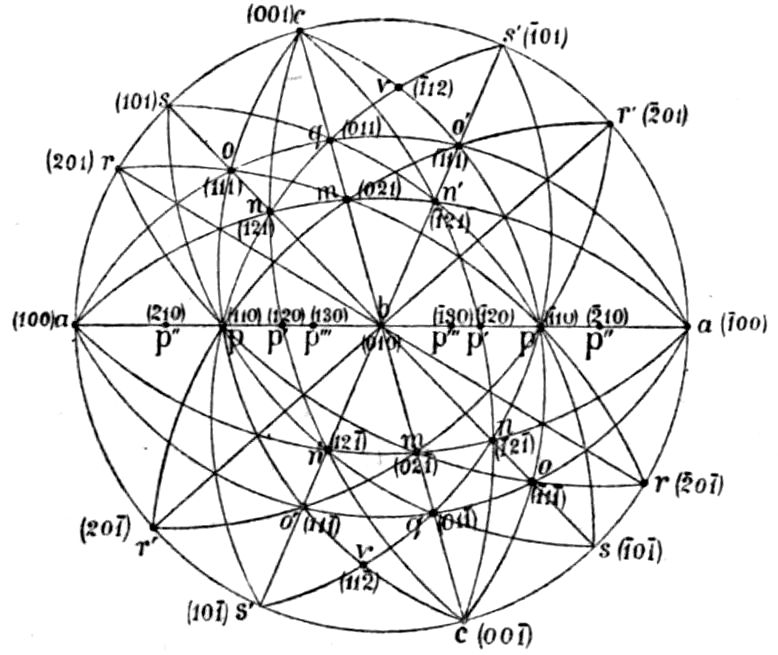
Fig. 16.—Projection of Potassium Nickel Sulphate and its Isomorphous Analogues.
Thus in Fig. 15 is represented a crystal of the
salt potassium nickel sulphate, K2Ni(SO4)2.6H2O,
belonging to the monoclinic
system of symmetry, and
which, therefore, possesses
only one plane of symmetry.
In Fig. 16 its stereographic
projection is shown, in which
each face in one of the symmetrical
halves is represented
by a dot, the plane of symmetry,
parallel to the face b, being the plane of the
paper, so that each dot not on the circumference
really represents two symmetrical faces, one above
and one below the paper, while the circumferential
dots represent faces perpendicular to the symmetry
plane and paper. The mode of arriving at such
a useful projection, or plan of the faces, will be
discussed more fully
later in Chapter VI.
But for the present
purpose it will be
sufficient to note that
the right and left
halves of the crystal
shown in Fig. 15 are
obviously symmetrical
to each other, and
that the plan of either
half, projected on the
dividing plane of symmetry
itself, may be taken as given in Fig. 16;
that is, we may imagine the crystal shown in
36Fig. 15 to be equally divided by a section plane
which is vertical and perpendicular to the paper
when the latter is held up behind the crystal and in
front of the eye, this section plane being the plane of
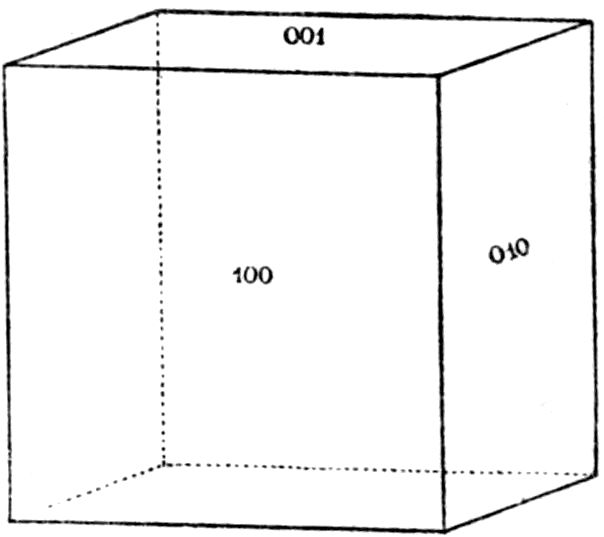
symmetry and parallel to the face b = (010). It may
thus be imagined as the plane of projection of Fig. 16.
An axis of symmetry is a direction in the crystal
such that when the latter is rotated for an angle of
60°, 90°, 120°, or 180° around it, the crystal is brought
to look exactly as it did before such rotation.
When a rotation for 180° is necessary in order to
reproduce the original appearance, the axis is
called a “digonal” axis of symmetry, for two
such rotations then complete the circle and bring
the crystal back to identity, not merely to similarity.
When the rotation into a position of similarity is for
120°, three such rotations are required to restore
identity, and the axis is then termed a “trigonal”
one. Similarly, four rotations to positions of
similarity 90° apart are essential to complete the
restoration to identity, and the axis is then a “tetragonal”
one, each rotation of a right angle causing
the crystal to appear as at first, assuming, as in all
cases, the ideal equality of development of faces.
Lastly, if 60° of rotation bring about similarity,
six such rotations are required in order to effect
identity of position, and the axis is known as a
“hexagonal” one.
Now, there is one system of symmetry which is
characterised by the presence of a single hexagonal
axis of symmetry, and this is the hexagonal system.
A crystal of this system, one of the naturally occurring
mineral apatite, which has been actually
37measured by the author, is shown in Fig. 17. There
is another system, the chief property of which is to
possess a tetragonal axis of symmetry, and which is
therefore termed the tetragonal system. A tetragonal
crystal of anatase, titanium dioxide, TiO2, which
has likewise been measured on the goniometer by
the author, is shown in Fig. 18. And there is yet
another system, the trigonal, the chief attribute
of which is the possession of a single trigonal axis
of symmetry, and which is consequently named the
trigonal system. In Fig. 19 is shown a crystal of
calcite, within which the directions of the three
rhombohedral crystallographic axes of the trigonal
system, and that of the vertical trigonal axis of
symmetry, are indicated in broken-and-dotted lines.
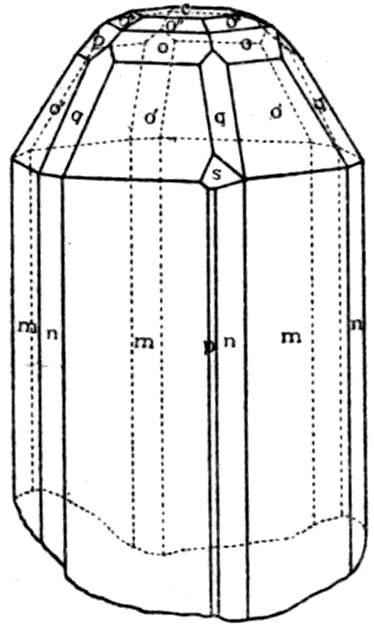
Fig. 17.—Measured Crystal of Apatite.
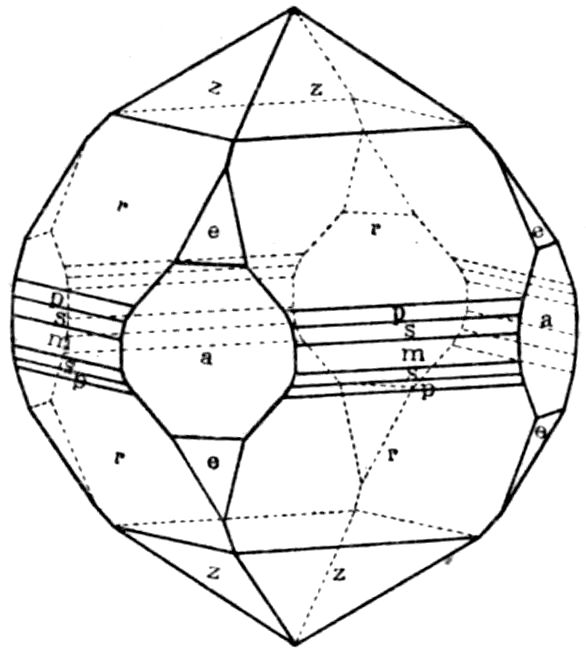
Fig. 18.—Measured Crystal of Anatase.
But there is one system of symmetry, the highest
possible, and which has already been referred to as
the cubic system, which combines in itself all but one
(the hexagonal axis) of the elements of symmetry. Indeed,
not only does it possess a tetragonal, a trigonal,
and a digonal axis of symmetry, but also ten other
38symmetry axes; for these three automatically involve
altogether the presence of no less than three tetragonal,
four trigonal, and six digonal axes of symmetry,
together with nine planes of symmetry, twenty-two
elements of symmetry being thus present in all.
The perfections of the cube, the simple lines of
which are illustrated in Fig. 20, as the expression of
the highest kind of symmetry, with angles all right
angles and sides and edges all equal, were so fully
appreciated by the geometrical minds of the ancient
Greek philosophers, imbued with the innate love
of symmetry characteristic of their nation, that to
them the cube became the emblem of perfection.
We are reminded of this interesting fact in the Book
of Revelation, which, in describing in its inimitable
language the wonders of the Holy City, speaks of
it as “lying foursquare,” and attributes to it the
properties of the cube, that “The length and the
breadth and the height of it are equal.”
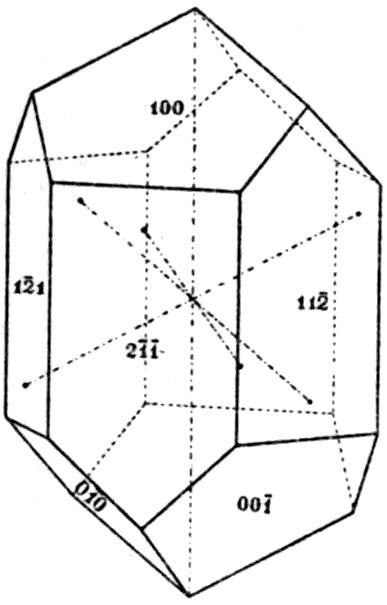
Fig. 19.—Crystal of Calcite.
Fig. 21.—The Hexakis Octahedron.
The full symmetry of the cubic system is not
realised, however, by a study of the cube alone;
39we only appreciate it when we come to examine
the general form of the cubic system, that which is
produced by starting with a face oblique to all
three axes, and with different amounts of obliquity
to each, and seeing how many repetitions of the
face the symmetry demands. The presence of
such a face involves as a matter of fact, when all
the elements of symmetry are satisfied, the presence
also of no less than forty-seven others, symmetrically
situated, the forty-eight-sided
figure produced being the
hexakis octahedron shown in
Fig. 21, and which is occasionally
actually found developed
in nature as the diamond. All
diamonds do not by any means
exhibit this form so wonderfully
rich in faces, but diamonds
are from time to time found
which do show all the forty-eight
faces well developed.
Fig. 22.—Measured Crystal of Topaz.
Besides these four more highly symmetrical
systems or styles of crystal architecture, a fifth,
the monoclinic system, characterised by a single
plane of symmetry and one axis of digonal symmetry
perpendicular thereto, has already been alluded to,
and a typical crystal illustrated in Fig. 15. A sixth,
the rhombic system, perhaps in some ways the most
interesting of all, and certainly so optically, possesses
three rectangular axes of symmetry, identical
in direction with the crystallographic axes, and
three mutually rectangular planes of symmetry,
coincident with the axial planes and intersecting each
40other in the axes. The lengths of the three crystal
axes are unequal, however, and herein lies the essential
difference from the cube. A
very typical rhombic substance
is topaz, a crystal of which,
about three millimetres in
diameter, is shown very much
enlarged in Fig. 22. Every
face on this crystal has been
actually investigated on the
goniometer, and the interfacial
angles measured.
Fig. 23.—Measured Crystal of Copper Sulphate.
Lastly, there is the seventh, the triclinic system,
in which there are neither planes nor axes of symmetry,
but, even in its holohedral class, only symmetry
about the centre, each face having a parallel
fellow. Sulphate of copper, blue vitriol, CuSO4.5H2O,
shows this type of symmetry, or rather lack of it,
very characteristically, and a crystal of this beautiful
deep blue salt, measured by the
author, is represented in Fig. 23.
Hence, we have arrived logically at
seven systems of symmetry or styles of
crystal architecture, distinguished by
the nature of their essential axes of
symmetry, and the planes of symmetry
which may accompany them. Now
the full degree of symmetry of each
system may be reduced to a certain
minimum without lowering the system,
and in all the systems but the triclinic
there are several definite stages of reduction before
the minimum is reached, each stage corresponding to
one of the thirty-two classes of crystals. Thus in
the cubic system there are four classes besides the
holohedral, in the tetragonal six, in the hexagonal
four, in the trigonal six, in the rhombic and monoclinic
two each, and in the triclinic one.
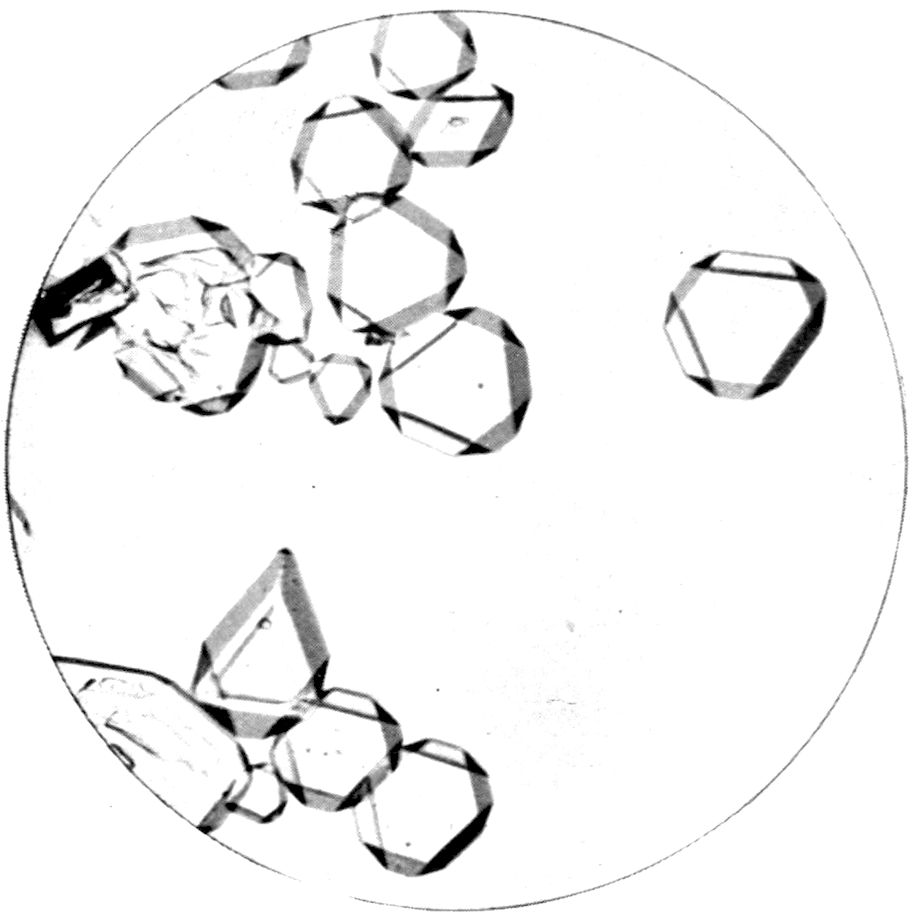
PLATE IV.
Fig. 24.—Octahedra of Potassium Cadmium Cyanide.

Fig. 25.—Octahedra of Cæsium Alum.
Cubic Crystals growing from Solution.
41We have thus attained at length to a truly
scientific classification of crystal forms, by using
axes and planes of symmetry as criteria. There
is no occasion whatever to imagine suppression of
faces in the classes of lower than the holohedral
or highest symmetry of any system. In these
classes it is simply the fact that less than the full
number of elements of symmetry possible to the
system are present and characterise the class, which
still conforms, however, to the minimum symmetry
absolutely essential to the system.
The drawings of crystals of the seven systems
in the foregoing illustrations will have given a
correct idea of the nature of the symmetry in each
case. But now it may be much more interesting
to present a series of reproductions of photographs
of some actual crystals of the different systems. Such
a series is given in Figs. 24 to 33, Plates IV. to VIII.
They were taken with the aid of the microscope,
the substances being crystallised from a slightly
supersaturated solution in each case, on a microscope slip.
A ring of gold size was first laid on
the slip, and allowed to dry for several days.
The drop of solution, in the metastable supersaturated
condition (corresponding to the region of
solubility which lies between the solubility and supersolubility
curves, Fig. 98, page 240), was placed in the
middle of the ring, and crystallisation just allowed to
42start, either owing to evaporation and consequent production
of the labile condition for spontaneous crystallisation,
or by access of a germ crystal from the air.
It was then covered with a cover-glass, which had the
desired effect of enclosing the solution in a parallelsided
cell, a film of the thickness of thick paper,
suitable for undistorted microscopic observation and
photomicrography, and also the effect of arresting
evaporation and therefore the rapidity of the growth
of the crystals, so that a photomicrograph taken with
the minimum necessary exposure was quite sharp.
The crystals shown in the accompanying photographic
reproductions, Figs. 24 to 33 (Plates IV. to
VIII.), as well as Fig. 4 (Plate II.), already described,
were thus photographed in the very act
of slow growth, employing a one-inch objective
very much stopped down. Such photographs
are infinitely sharper and more beautifully and
delicately shaded than those taken of dry crystals.
Fig. 24, Plate IV., represents cubic octahedra of
the double cyanide of potassium and cadmium,
2KCN.Cd(CN)2, a salt which crystallises out in
relatively large and wonderfully transparent and well-formed
single octahedra on a micro-slip, and is particularly
suitable for demonstrating the character of
this highest system, the cubic, of crystal symmetry.
Special development of the pair of faces of the octahedron
parallel to the glass surfaces has occurred,
owing to greater freedom of growth at the boundaries
of these faces, as is usual in such circumstances of
deposition, but the other pairs of faces are quite large
enough to show their nature clearly.
Fig. 25, on the same Plate IV., shows a slide of
cæsium alum, Cs2SO4.Al2(SO4)3.24H2O, in which the
octahedra are smaller, and some of them, notably one
in the centre of the field, are perfectly proportioned.

PLATE V.
Fig. 26.—Octahedra of Ammonium Iron Alum crystallising on a Hair.
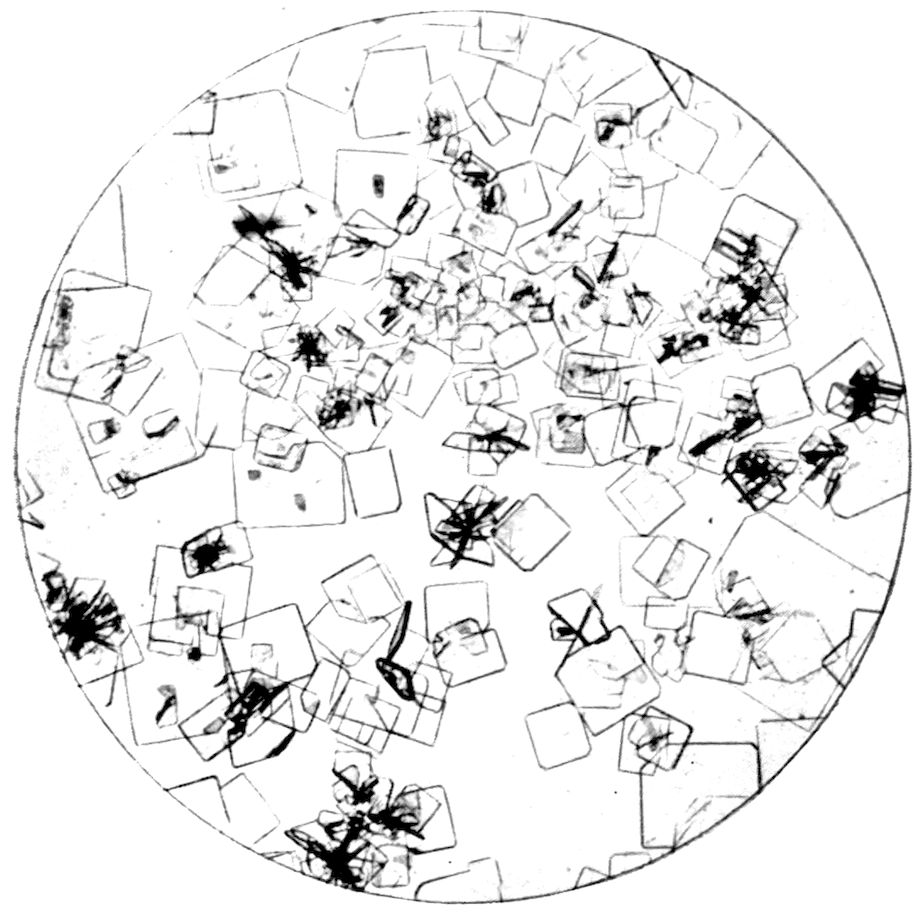
Fig. 27.—Tetragonal Crystals of Potassium Ferrocyanide.
Crystals growing from Solution.
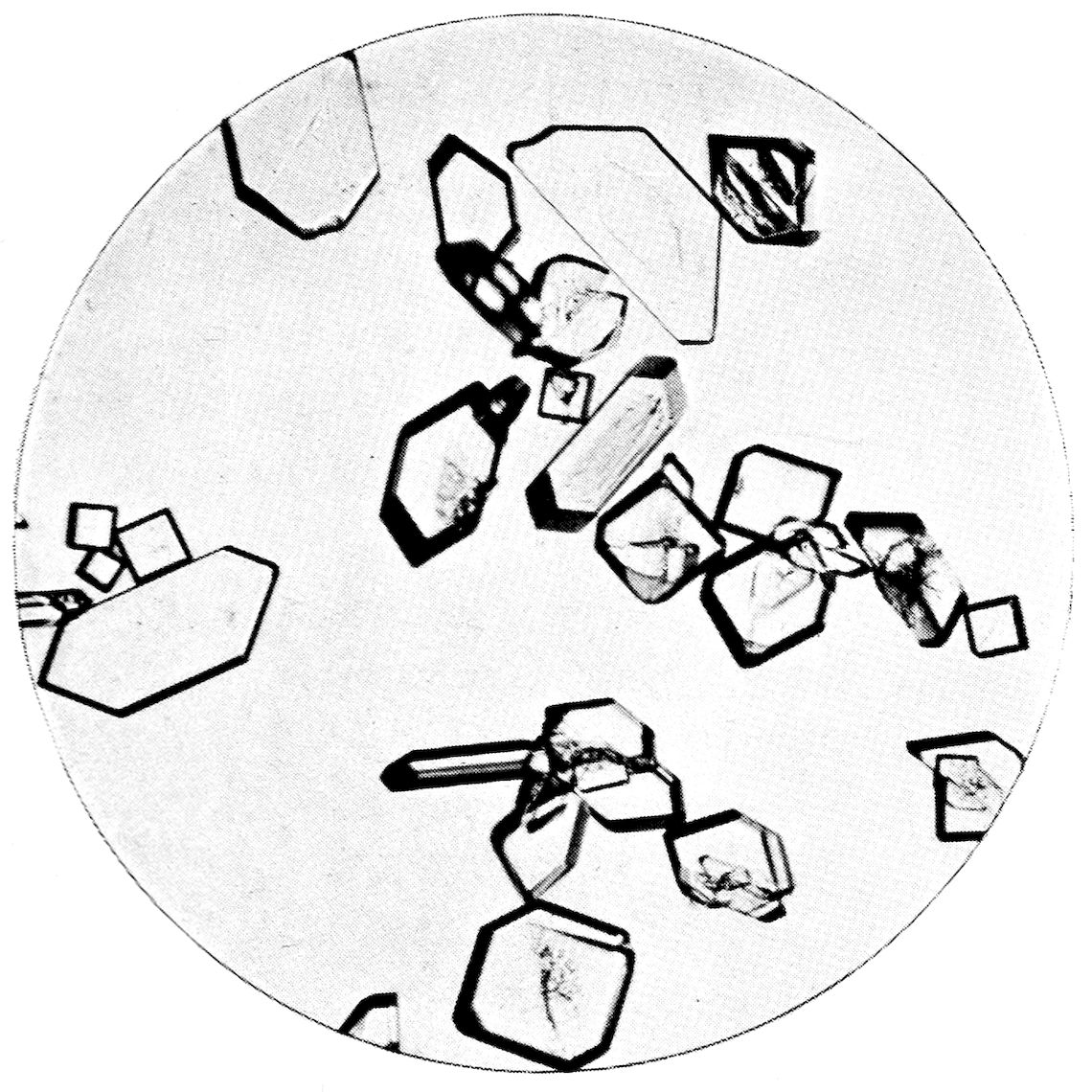
PLATE VI.
Fig. 28.--Rhombic Crystals of Potassium Hydrogen Tartrate.
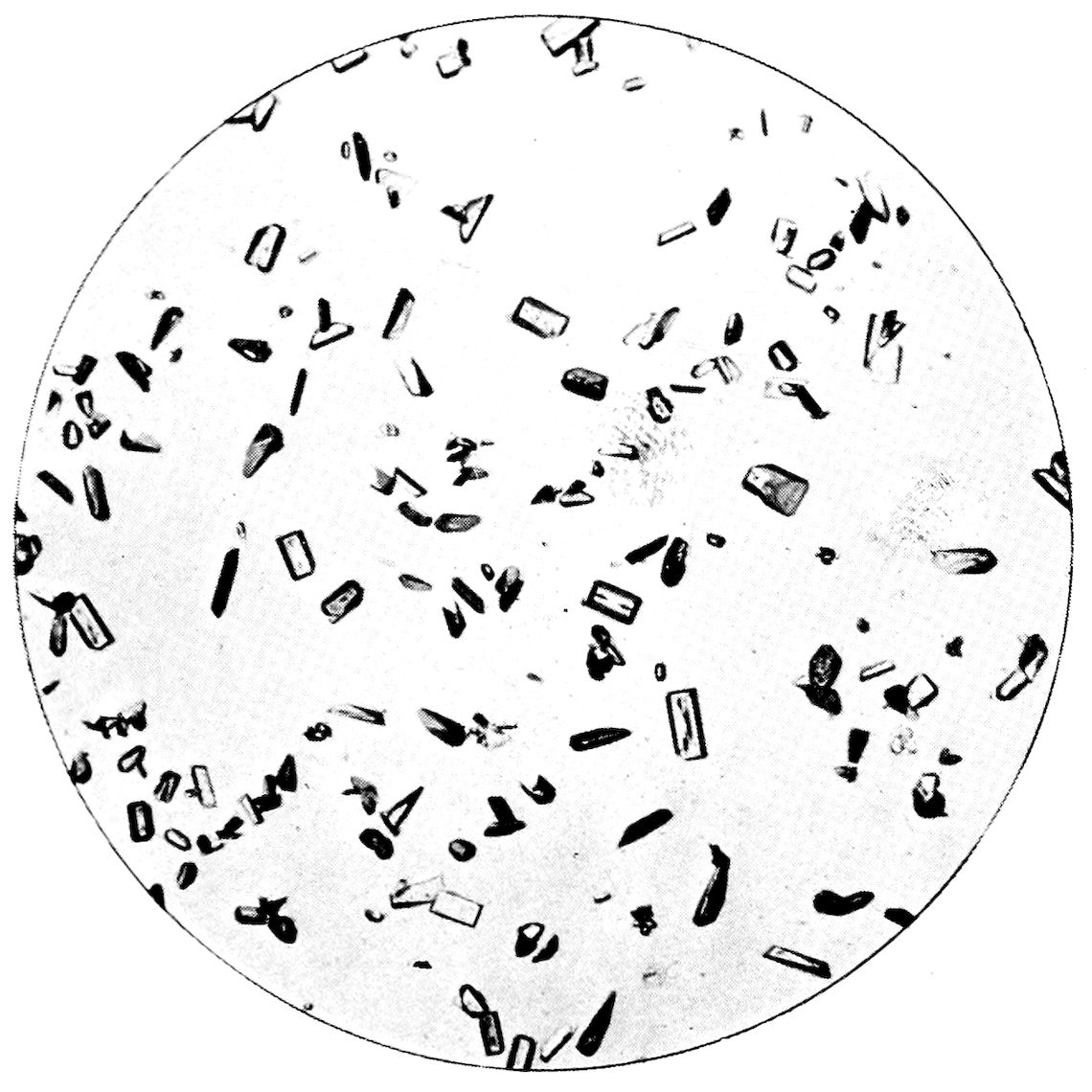
Fig. 29.--Rhombic Crystals of Ammonium Magnesium Phosphate, showing Special Growth along Line of Scratch.
Rhombic Crystals growing by Slow Precipitation.
43Fig. 26, Plate V., represents octahedra of ammonium
iron alum (formula like that of cæsium
alum, but with NH4 replacing Cs and Fe replacing
Al) crystallising on a hair. It illustrates the interesting
manner in which crystallisation will sometimes
occur, under conditions of quietude, when some object
or other on which the crystals can readily deposit
themselves is present or introduced, such as a silk
or cotton thread, or a hair as in this case.
Fig. 27, on the same Plate V., represents tetragonal
crystals of potassium ferrocyanide, K4Fe(CN)6, composed
of tabular crystals parallel to the basal pinakoid,
bounded by faces of one order, first or second, of
tetragonal prism, the corners being modified at 45° by
smaller faces of the other order of tetragonal prism.
Fig. 28, Plate VI., is a photograph of large rhombic
crystals of hydrogen potassium tartrate, HKC4H4O6,
obtained by addition of tartaric acid to a dilute
solution of potassium chloride. They are rectangular
rhombic prisms capped by pyramidal forms, and also
modified by other prismatic and domal forms.
Fig. 29, also on Plate VI., represents another
rhombic substance, ammonium magnesium phosphate,
NH4MgPO4.6H2O, obtained by very slow precipitation
of a dilute solution of magnesium sulphate
containing ammonium chloride and ammonia with
hydrogen disodium phosphate. It illustrates in an
interesting manner how, when a saturated solution
is kept quiet, and then the surface of the vessel containing
it is scratched by a needle point, a line of small
crystals at once starts forming along the line of
scratch, even although the latter has made no actual
44impression on the glass itself. Such a line of crystals
will be observed running across the middle of the slide.
Fig. 30, Plate VII., shows a monoclinic substance,
ammonium magnesium sulphate (NH4)2Mg(SO4)2.6H2O,
which crystallises out splendidly on a micro-slip.
The field includes several very well-formed
typical crystals of the salt, which is one of the same
exceedingly important isomorphous series to which
potassium nickel sulphate, Fig. 15, belongs; it is
obtained by mixing solutions containing molecularly
equivalent quantities of ammonium and magnesium
sulphates. The primary monoclinic prism is the chief
form, terminated by clinodome faces and smaller strip-faces
of the basal plane, the latter, however, being
occasionally the chief end form. Small pyramid faces
are also seen here and there modifying the solid angles.
Another beautifully crystallising monoclinic substance
is shown in the next slide, Fig. 31, on the
same Plate VII., namely, potassium sodium carbonate,
KNaCO3.6H2O, obtained from a solution of
molecular proportions of potassium and sodium
carbonates. Numerous forms of the monoclinic
system are developed, on relatively large and perfectly
transparent and delicately shaded individuals.
A triclinic substance is represented in Fig. 32,
Plate VIII., potassium ferricyanide, K6F2(CN)12.
The triply oblique nature of the symmetry is clearly
exhibited by this salt, the absence of any right
angles being very marked.
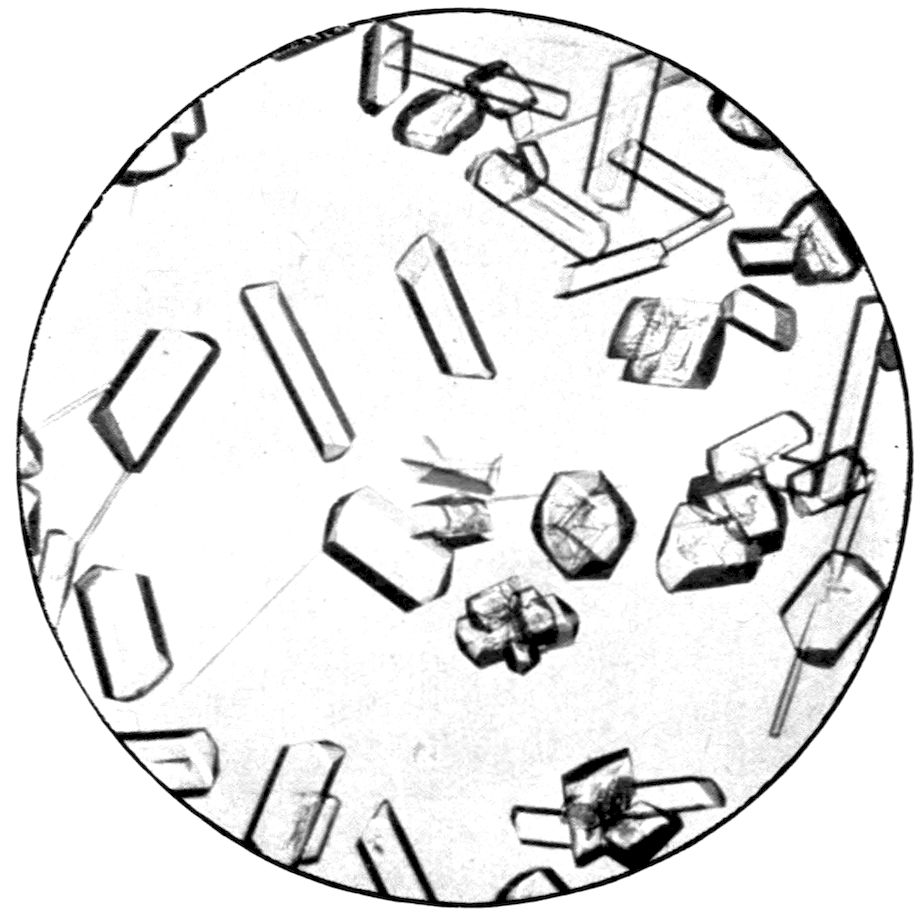
PLATE VII.
Fig. 30.—Monoclinic Crystals of Ammonium Magnesium Sulphate.

Fig. 31.—Monoclinic Crystals of Sodium Potassium Carbonate.
Monoclinic Crystals growing from Solution.
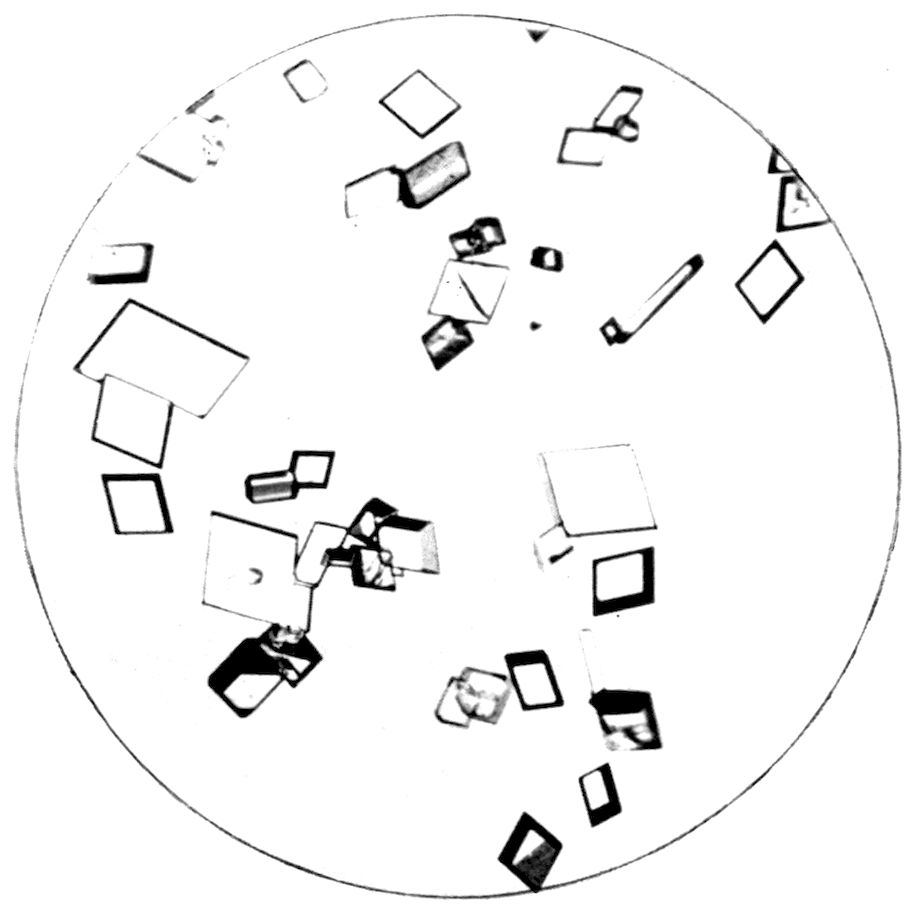
PLATE VIII.
Fig. 32.—Triclinic Crystals of Potassium Ferricyanide.
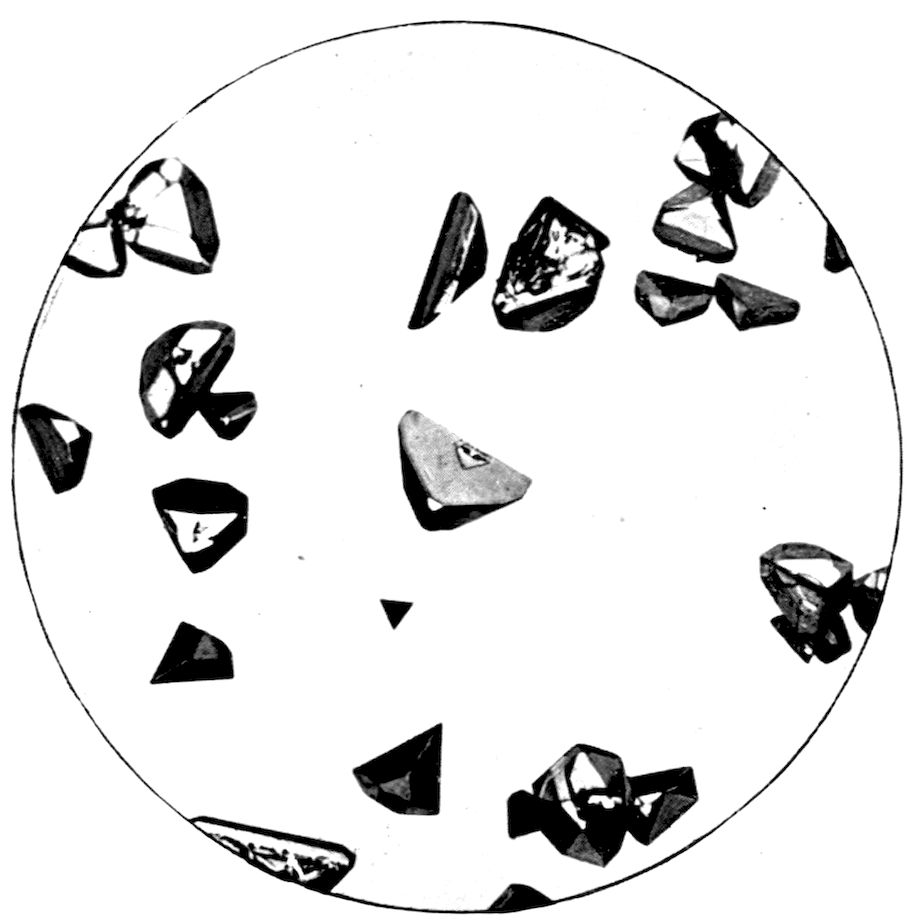
Fig. 33.—Tetrahedral Crystals of Sodium Sulphantimoniate, Cubic Class 28.
Crystals growing from Solution.
45Fig. 33, also on Plate VIII., illustrates more particularly
a class of one of the systems, the cubic,
which is of lower than holohedral (full) systematic
symmetry. This is the case also with hydrogen potassium
tartrate and ammonium magnesium phosphate,
but the forms shown of those salts on the slides represented
in Figs. 28 and 29 are chiefly those which
are also common to the holohedral classes of their
respective systems, and the lower class symmetry is
not emphasised. But here in Fig. 33, representing
Schlippe’s salt, sodium sulphantimoniate, Na3SbS4.9H2O,
we have very clear development of the
tetrahedron, belonging to the lowest of the five
classes (class 28) of the cubic system. The crystals
are almost all combinations of two complementary
tetrahedra, one of which is developed so very much
more than the other that the faces of the latter
only appear as minute replacements at the corners
of the predominating tetrahedron.
This is the last for the present of these fascinating
growths of crystals under the microscope, but
three more will be given subsequently, in Figs. 99
and 100, on Plate XXI., and Fig. 101, Plate XI., to
illustrate crystallisation from metastable and labile
solutions.
Fig. 34, Plate IX., represents another kind of
phenomenon, equally instructive. It shows a field
in a crystal of quartz, as seen under the same power
of the microscope, a one-inch objective with small
stop and an ordinary low power eyepiece. Just above
and to the left of the centre of the field is a cavity,
the shape of which is remarkable, for it is that of
a quartz crystal, a hexagonal prism terminated by
rhombohedral faces. The cavity is filled with a
saturated solution of salt, except for a bubble of water
vapour, and a beautiful little cube of sodium chloride
which has crystallised out from the solution. This
slide, therefore, gives us an example of a natural
cubic crystal, and also an indication of the shape
46of quartz crystals, the cavity itself being a kind
of negative quartz crystal. The crystal in which
it occurs must have been formed very deep
down in a reservoir of molten material beneath
a volcano, under the great pressure of superincumbent
rock masses. It was probably one of the
quartz crystals of a granite rock which had crystallised
under these conditions. Almost every crystal
of quartz found in such granite rocks displays
thousands of small cavities filled with liquid and
a bubble, although it is very rare to find one with
so good a cube of salt and having the configuration
of a quartz crystal for the shape of the cavity.
Many such cavities, however, contain as the liquid
compressed carbonic acid, the very fact of the
carbonic acid being in the liquefied state affording
ample evidence of the pressure under which
the crystal was formed. The proof that the liquid is
carbonic acid in these cases is afforded by the fact
that when the crystal is warmed to 32°C., the
critical temperature of carbon dioxide, under which
it can no longer remain liquid, but must become a
gas, the bubble disappears and the cavity becomes
filled with gas. Carbonic acid cavities are readily
recognised, inasmuch as the bubble is extremely
mobile, and is normally in a state of movement
on the very slightest provocation.
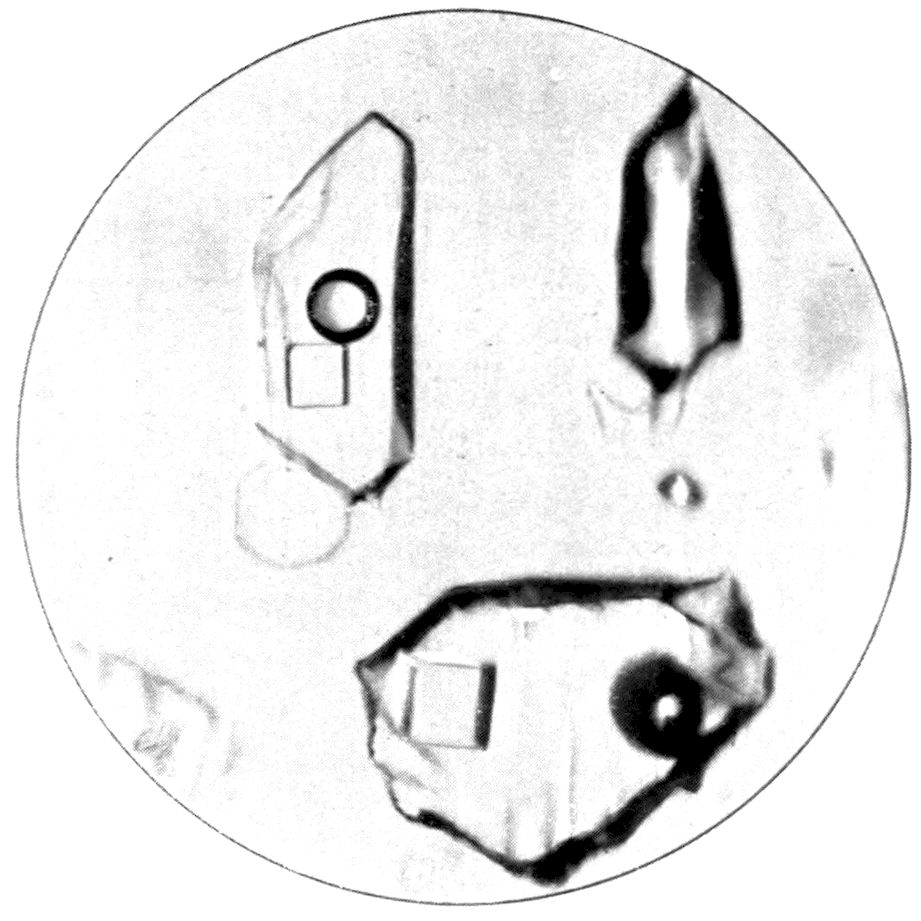
PLATE IX.
Fig. 34.—Liquid Cavities in quartz Crystal (Trigonal) containing Saturated Solution and Cubic Crystals of Sodium Chloride.

Fig. 36.—Two characteristic Forms of Snow Crystals (Trigonal).
47

Fig. 35.—Negative Ice Crystals, or “Water Flowers,” in Ice.
The liquid cavity in the remarkable quartz crystal
illustrated in Fig. 34, and the bubble of vapour formed
on cooling, and consequent contraction of the liquid
more than the solid quartz (the thermal dilatation of
liquids being usually greater than that of solids) when
it was no longer able to fill the cavity, remind one of
the beautiful water flowers formed for the contrary
reason in ice on passing a beam of light through a
slab, owing to the warming effect of the accompanying
heat rays. Water crystallises like quartz, in the
trigonal system, its normal forms being the hexagonal
prism and the rhombohedron. A slab of lake ice is
generally a huge crystal plate perpendicular to
the trigonal axis, or in the case of disturbed growth
an interlacing mass of such crystals, all perpendicular
to the optic axis, the axis of the hexagonal
prism and of trigonal symmetry. When the heat
rays from the lantern pass through such a slab of
ice, the surface of which is focussed on the screen
by a projecting lens, they cause the ice to begin to
melt in numerous spots in the interior of the slab
simultaneously; and the structure of the crystal
is revealed by the operation occurring with production
of cavities taking the shape of hexagonal stars,
which when focussed
appear on the screen
as shown in Fig. 35.
They are filled with
water except for a
bubble (vacuole),
which contains only
water vapour. For
the liquid water occupies
less room than
did the ice from which
it was produced, owing
to the well-known
fact that water expands
on freezing.
This abnormal expansion with cooling begins at the
temperature of the maximum density of water,
484° C., and proceeds steadily until the freezing point
0° is reached, when, at the moment of crystallisation,
the mass suddenly increases in volume by as much
as 10 per cent. This expansive leap when the
molecules of water marshal themselves into the
organised order of the homogeneous structure, that
of the space-lattice of the trigonal (rhombohedral)
system, is one of the most remarkable phenomena
in nature, and its exceptional character,
so contrary to the usual contraction on solidification
of a liquid, is of vital moment to aquatic life.
For the layer of ice formed, being lighter than
water, floats on the surface of the latter, and thus
forms a protective layer and prevents to a large
extent further freezing, except as a slow thickening
of the layer, the total freezing of the water of a
lake or river being rendered practically impossible,
an obvious provision for the security of life of the
piscatorial and other inhabitants of the waters.
Hence, as the molecules of the substance H2O are
one by one detached from their solid assemblage as ice,
and become more loosely associated as the less voluminous
liquid water, they cannot occupy the whole
of the cavity formed in the solid ice, and a small
vacuous space, occupied only by water vapour at its
ordinary low tension corresponding to the low temperature,
is formed and appears as the bubble. Moreover,
the cavity itself takes the shape of a hexagonal
star-shaped flower, the bubble showing at its centre,
the cavity being thus a kind of negative ice crystal,
like the negative quartz crystal shown in Fig. 34.
Apparently in the production of these cavities,
just as in the production of the well-known etched
figures on crystal faces by the application of a
minute quantity of a solvent for the crystal substance,
the crystal edifice is taken down, molecule
by molecule, in a regular manner, resulting in the
formation of a cavity showing the symmetry of the
space-lattice which is present in the crystal structure.

PLATE X.
Fig. 37.—Piz Palü and Snow-field of the Pers Glacier, from the Diavolezza Pass, Upper Engadine.
(From a Photograph by the author.)
49The water flowers of Fig. 35 remind one very much
of snow crystals, two of which, re-engraved from the
wonderfully careful drawings of the late Mr Glaisher,
are represented in Fig. 36, Plate IX. They all exhibit
the symmetry of the hexagonal prism, which is equally
a form of the trigonal system as it is of the hexagonal
system. The snow crystals, being formed from water
vapour condensed in the cold upper layers of the
atmosphere, appear more or less as skeleton crystals,
owing to the rarity of the semi-gaseous material condensed,
compared with the extent of the space in
which the crystallisation occurs. Indeed the exquisite
tracery of these snow crystals appears to afford a
visual proof of the existence of the trigonal-hexagonal
space-lattice as the framework of the crystal structure
of ice. When one considers the countless numbers of
such beautiful gems of nature’s handiwork massed
together on an extensive snow-field of the higher
Alps—such as that of the Piz Palü in the Upper
Engadine, shown in Fig. 37, Plate X., as seen from
the Diavolezza Pass—produced in the pure air of
the higher regions of the atmosphere, and frequently
seen by the early morning climber lying
uninjured in all their beauty on the surface of the
snow-field, one is lost in amazement at the prodigality
displayed in the broadcast distribution of
such peerless gems.
50
CHAPTER V
HOW CRYSTALS ARE DESCRIBED. THE SIMPLE LAW LIMITING THE NUMBER OF POSSIBLE FORMS.
The most wonderful of all the laws relating to
crystals is the one already briefly referred to which
limits and regulates the possible positions of faces,
within the lines of symmetry which have been
indicated in the last chapter. Having laid down
the rules of symmetry, it might be thought that any
planes which obey these laws, as regards their
mode of repetition about the planes and axes of
symmetry, would be possible. But as a matter of
fact this is not so, only a very few planes inclined
at certain definite angles, repeated in accordance
with the symmetry, being ever found actually
developed. The reason for this is of far-reaching
importance, for it reveals to us the certainty that
a crystal is a homogeneous structure composed of
definite structural units of tangible size, probably
the chemical molecules, built up on the plan of one
of the fourteen space-lattices made known to us by
Bravais, and to be referred to more fully in Chapter
VIII. In order to render this fundamental law
comprehensible, it will be essential to explain in a
few simple words how the crystallographer identifies
and labels the numerous faces on a crystal, in short,
how he describes a crystal, in a manner which shall
51be understood immediately by everybody who has
studied the very simple rules of the convention.
It is a matter of common knowledge that the
mathematical geometrician defines the position of
any point in space with reference to three planes,
which in the simplest case are all mutually at right
angles to each other like the faces of a cube, and which
intersect in three rectangular axes a, b, c, the third
c being the vertical axis, b the lateral one, and a the
front-and-back axis. The distances of the point
from the three reference planes, as measured by the
lengths of the three lines drawn from the point to
the planes parallel to the three axes of intersection,
at once gives him what he calls the “co-ordinates”
of the point, which absolutely define its position. In
the same way we can imagine three axes drawn
within the crystal, by which not only the position
of any point on any face of the crystal may be
located, but which may be used more simply still
to fix the position of the face itself. The directions
chosen as those of the three axes are the edges of
intersection of three of the best developed faces.
If there are three such faces inclined at right
angles they would be chosen in preference to all
others, as they would certainly prove to be faces
of prime significance as regards the symmetry of the
crystal. If there are no such rectangularly inclined
faces developed on the crystal, then the three best
developed faces nearest to 90° to each other are
chosen, the two factors of nearness to rectangularity
and excellence of development being simultaneously
borne in mind in making the choice of axial planes,
and discretion used.
52
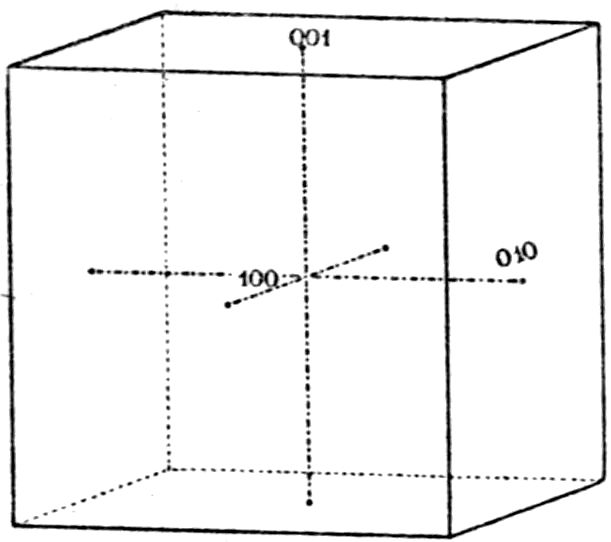
Fig. 38.—The Cube and its Three Equal Rectangular Axes.
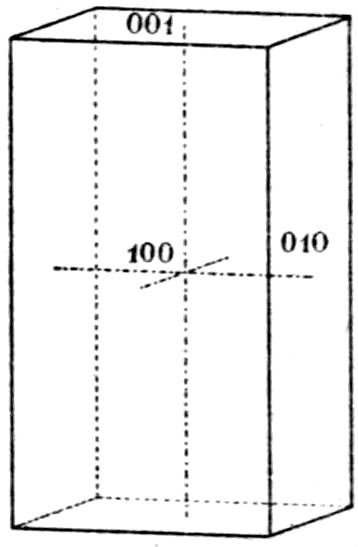
Fig. 39.—Tetragonal Prism and its three Rectangular Axes.
If the crystal belong to the cubic, tetragonal,
or rhombic systems, for instance, three faces
meeting each other rectangularly are possible
planes on the crystal, and will very frequently be
found actually developed; such would obviously
be chosen as the axial planes. The edges of the
cube, or of the tetragonal or rectangular rhombic
prism, will be the directions of the crystallographic
axes in this case, and we can imagine them moved
parallel to themselves until the common centre
of intersection, the “origin” of the analytical
geometrician, will occupy the centre of the crystal,
and the faces of the latter be built up symmetrically
about it. When the crystal is cubic, the three
axes will be of equal length as shown in Fig. 38;
if tetragonal, the two horizontal axes will be equal,
but will differ in length from the vertical axis, as
represented in Fig. 39. If the crystal be rhombic,
all three axes will be of different lengths, as indicated
in Fig. 40, which represents the axes and axial planes
53of an actual rhombic substance, topaz, for which the
lateral axis b and vertical axis c are nearly but not quite
equal, while the front-and-back axis a is very different.
When the crystal is of monoclinic symmetry,
as in Fig. 41, three axes will similarly be found as
the intersection of three principal parallel pairs
of faces, but two of them will be inclined at an angle
other than 90° to each other, while the third, the
lateral one in Fig. 41, will be at right angles to those
first two and to the plane containing them; moreover,
all three are unequal in length. In the case
of a triclinic crystal, shown in Fig. 42, however,
there can be no right angles, and the intersections
of three important faces meeting each other at
angles as near 90° as possible are chosen as the axes,
regard being had to both factors of approximation
to rectangularity and importance of development.
These triclinic axes are the most general type of
crystal axes, for not only are the angles not right
angles, but the lengths of the axes are also unequal.
54
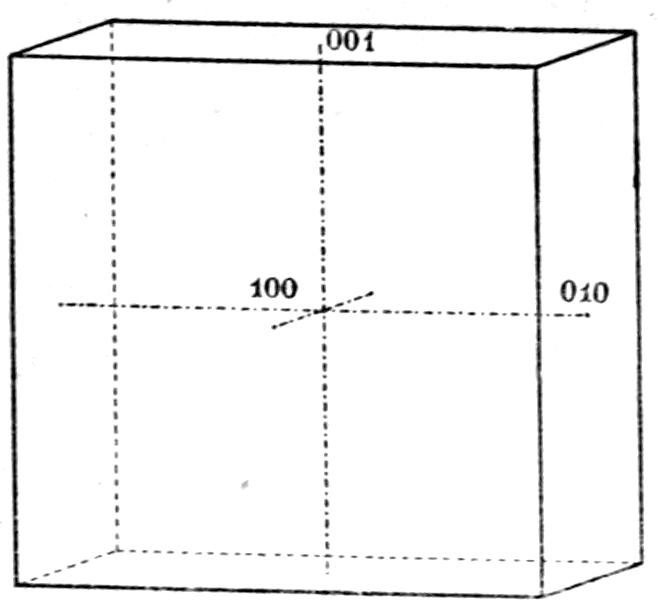
Fig. 40.—Axial Planes of a Rhombic Crystal.
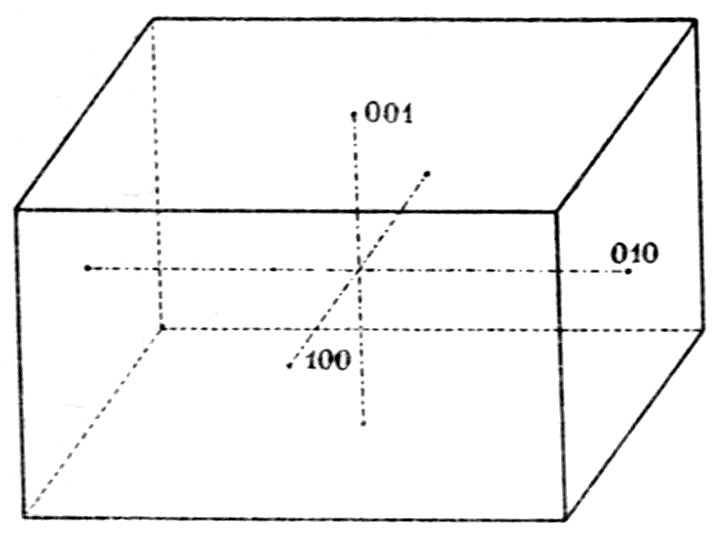
Fig. 41.—Axial Planes of a Monoclinic Crystal.
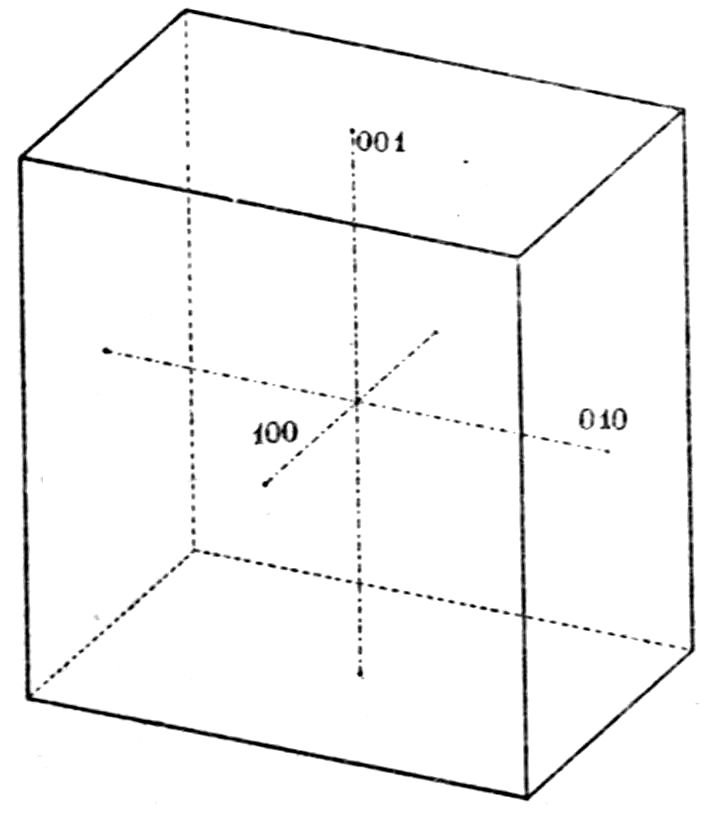
Fig. 42.—Axial Planes of a Triclinic Crystal.
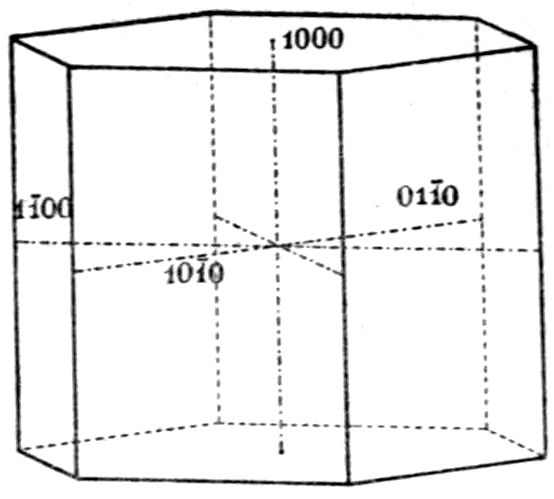
Fig. 43.—Hexagonal Prism of the First Order and its Four Axes.
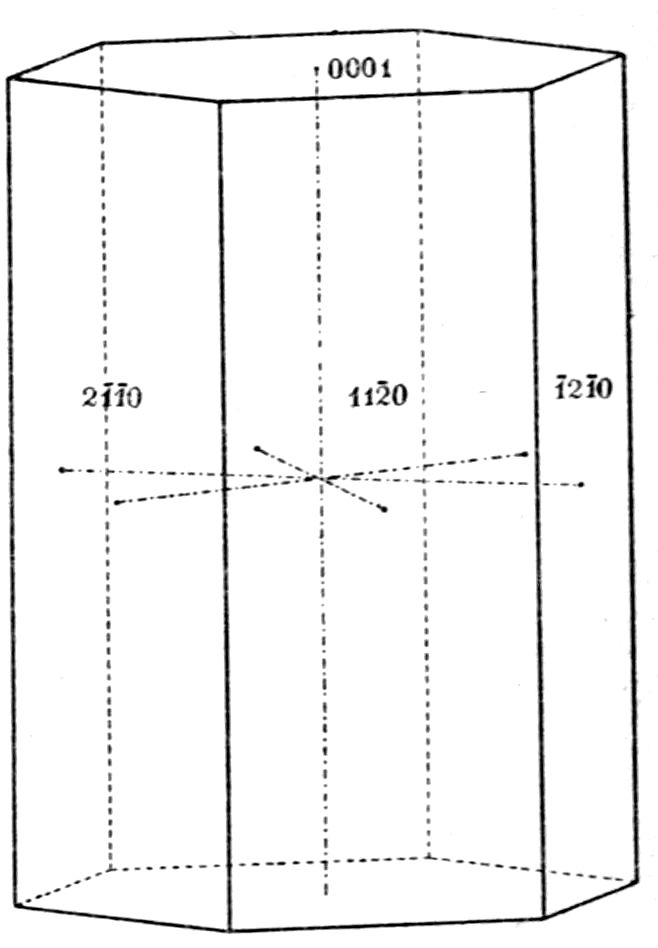
Fig. 44.—Hexagonal Prism of the Second Order.
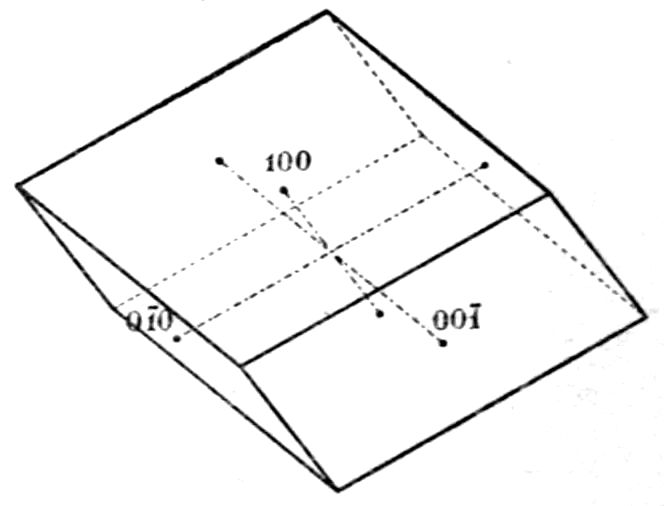
Fig. 45.—The Rhombohedron and its Three Equal Axes.
55The cases of the hexagonal and trigonal systems
are somewhat special. The hexagonal has four
such axes, as represented in Fig. 43, the lines of
intersection of the faces of the hexagonal prism
closed by a pair of perpendicular terminal planes,
namely, one vertical axis parallel to the vertical
edges, and three horizontal axes inclined at 120°
to each other, and parallel to the pair of basal plane
faces, equal to each other in length, but different
from the length of the vertical axis. The hexagonal
axial-plane prism shown in Fig. 43 is known as one
of the first order. The hexagonal prism corresponding
to the tetragonal one of Fig. 39, in which the
axes emerge in the centres of the faces, is said to be
of the second order, and is shown in Fig. 44. The
trigonal system of crystals is best described with reference
to three equal but not rectangular axes, parallel
to the faces of the rhombohedron, one of the principal
forms of the system, so well seen in Iceland
spar, and illustrated in Fig. 45. The rhombohedron
may be regarded as a cube resting on one of its
corners (solid angles), with the diagonal line joining
this to the opposite corner vertical, and the cube
then deformed by flattening or elongating it along
the direction of this diagonal. The edges meeting
at the ends of this vertical diagonal are then the
directions of the three trigonal crystallographic axes.
In this last illustration the vertical direction of
the altered diagonal is that of the trigonal axis of
symmetry, for the rhombohedron is brought into
apparent coincidence with itself again if rotated for
120° round this direction. But although a symmetry
axis, this is not a crystallographic axis of reference.
It is not shown in Fig. 45, therefore, but is
given in Fig. 19. On the other hand, the singular
vertical axis of reference of the tetragonal and
hexagonal systems is identical with the tetragonal or
hexagonal axis of symmetry of these systems, and the
three crystallographic axes of reference of the cube are
identical with the three tetragonal axes of symmetry
of the cubic system. In the rhombic system also,
the three rectangular axes of reference are identical
with the three digonal axes of symmetry, and in the
monoclinic system the one axis of reference which
is normal to the plane of the two inclined axes is
the unique digonal axis of symmetry of that system.
56Having thus evolved a scientific scheme of
reference axes for the faces of a crystal, it is necessary
in all the systems other than the cubic and trigonal,
in which the axes are of equal lengths, to devise
a mode of arriving at the relative lengths of the
axes; for on this depends the mode of determining
the positions of the various faces, other than the
three parallel pairs (or four in the case of the hexagonal
system) chosen as the axial planes. This is
very simply done by choosing a fourth important face
inclined to all three axes, when one of this character
is developed, as very frequently happens, as the
determinative face or plane
fixing the unit lengths of the
axes. When no such face is
present on the crystal, two
others can usually be found,
each of which is inclined to
two different axes, so that
between them all three axial
lengths are determined. The
faces of the octahedron, of the
primary tetragonal pyramid
and the primary rhombic pyramid, and of the corresponding
forms of the other systems, are such
determinative planes, fixing the lengths of the
axes. This fact will be clear from the typical
illustration of the most general of these primary or
“parametral” forms, the triclinic equivalent of the
octahedron, given in Fig. 46, the faces being obviously
obtained by joining the points marking unit
lengths of the three axes.

Fig. 46.—Triclinic Equivalent of the Octahedron.
Having thus settled the directions of the crystallographic
57axes and their lengths, it is the next step
which reveals the remarkable law to which reference
was made at the opening of this chapter. For we
find that all other faces on the crystal, however
complicated and rich in faces it may be, cut off
lengths from the axes which are represented by
low whole numbers, that is, either 2, 3, 4, or possibly
5, and very rarely more than 6 unit lengths. By
far the greater number of faces do not cut off more
than three unit lengths from any axis. Prof.
Miller of Cambridge, in the year 1839, gave us a
most valuable mode of labelling and distinguishing
the various faces by a symbol involving these three
values, employed, however, not directly but in an
indirect yet very simple manner. If m, n, r be the
three numbers expressing the intercepts cut off
by a face on the three axes, a, b, c respectively,
and if the Millerian index numbers be represented
by h, k, l, then—
| |
m = a
h, |
n = b
k, |
r = c
l, |
| or, |
h = a
m, |
k = b
n, |
l = c
r. |
Each figure or “index” of the Millerian symbol is
thus inversely proportional to the length of the
intercept on the axis concerned. The intercepts
themselves are used as symbols in another mode
of labelling crystal faces, suggested by Weiss, but
this method proves too cumbersome in practice.
The Millerian symbol of a face is always placed
within ordinary curved brackets ( ), but if the
symbol is to stand for the whole set of faces composing
the form, the brackets are of the type { }.
58Thus the Millerian symbol of the fourth face (that in
the top-right front octant), determinative of the unit
axial lengths, is (111), as shown in Fig. 46, the face
in question being marked with this symbol; while
the symbol {111} indicates the set of faces of the
whole or such part of the double pyramid as composes
the unit form. In the triclinic system this
form only consists of the face (111) and the parallel
one (̄1̄1̄1), but in the case of the regular octahedron
of the cubic system it embraces all the eight faces.
The triclinic octahedron, Fig. 46, is thus made up of
four forms of two faces each. A negative sign over
an index indicates interception on the axis a behind
the centre, on the axis b to the left of the centre, or
on the vertical axis c below the centre.
To take an actual example, suppose a face other
than the primary one to make the intercepts on the
axes 4, 2, 1; in this case h = a/4, k = b/2, and l = c/1,
that is, when referred to the fundamental primary
form for which a, b, c are each unity, h = ¼, k = ½,
l = 1, or, bringing them to whole numbers by multiplying
by 4, h = 1, k = 2, c = 4, and the symbol in
Millerian notation is (124). Again, suppose we
wish to find the intercepts on the three cubic axes
made by the face (321) of the hexakis octahedron
shown in Fig. 21. To get each intercept we multiply
together the two other Millerian indices, and if
necessary afterwards reduce the three figures
obtained to their simplest relative values. For the
face (321) we obtain 2, 3, 6. This means that the
face (321) in the top-right-front octant of the hexakis
octahedron cuts off two unit lengths of axis a,
three unit lengths of axis b, and six unit lengths of
59axis c. No fractional parts thus ever enter into
the relations of the axial lengths intercepted by
any face on a crystal, and the whole numbers
representing these relations are always small, the
number 6 being the usual limit.
This important law is known as the “Law of
Rational Indices,” and is the corner-stone of crystallography.
A forecast of it was given in Chapter III.,
in describing how it was first discovered by Haüy,
and it was shown how impressed Haüy was with
its obvious significance as an indication of the
brick-like nature of the crystal structure. What
the “bricks” were, Haüy was not in a position
to ascertain with certainty, as chemistry was in its
infancy, and Dalton’s atomic theory had not then
been proposed.
That Haüy had a shrewd idea, however, that the
structural units were the chemical molecules, and
that while the main lines of symmetry were determined
by the arrangement of the molecules its
details were settled by the arrangement of the
atoms in the molecules, is clear to any one who
reads his 1784 “Essai” and 1801 “Traité,” and
interprets his molécules intégrantes and élémentaires
in the light of our knowledge of to-day.
Before we pass on, however, to consider the
modern development of the real meaning of the law
of rational indices, as revealed by recent work on
the internal structure of crystals, it will be well to
consider first, in the next chapter, a few more
essential facts as to crystal symmetry, and the
current mode of constructing a comprehensive,
yet simple, plan of the faces present on a crystal.
60
CHAPTER VI
THE DISTRIBUTION OF CRYSTAL FACES IN ZONES, AND THE MODE OF CONSTRUCTING A PLAN OF THE FACES.
It will have been clear from the facts related in
the previous chapters that the salient property
possessed by all crystals, when ideal development
is permitted by the circumstances of their growth,
and the substance is not one of unusual softness
or liable to ready distortion, is that the exterior
form consists of and is defined by truly plane faces
inclined to each other at angles which are specific
and characteristic for each definite chemical substance;
and that these angles are in accordance
with the symmetry of some particular one of the
thirty-two classes of crystals, and are such as cause
the indices of the faces concerned to be rational
small numbers.
It will also be clear that, given the presence of
any face other than the three axial planes, the
symmetry of the class—supposing the crystal to
exhibit some development of symmetry and not
to belong to class 32, the general case possessing
no symmetry—will require the repetition
of this face a definite number of times on other
parts of the crystal. Such a set of faces possessing
the same symmetry value we have already learnt
to call a “Form,” and the faces composing it will
61have the same Millerian index numbers in their
symbols, but differently arranged and with negative
signs over those which relate to the interception
of the back part of the a axis, the left part of the
b axis, or the lower part of the vertical c axis; that
is, parts to the front and right, and above, the centre
of intersection of the three crystal axes are considered
as the positive parts of those axes.
A form, if of general character, that is, if composed
of faces each of which is inclined to all three
axes, will comprise more faces the higher the
symmetry. Thus, in the cubic system, the form
shown in Fig. 21, the hexakis octahedron, comprises
as many as forty-eight faces, all covered by the
form symbol {321}; while in the rhombic system
the highest number of faces in a form is eight, in the
monoclinic only four, and in the triclinic system two.
It will also have become clear that the law of
rational indices limits the number of forms possible
of any one type. For instance, very few hexakis
octahedra are known, the most frequently occurring
ones besides {321} being {421}, {531}, and {543}.
Forms, of any class, possessing higher indices than
these are very rare, especially in the systems of lower
symmetry.

Fig. 47.—The Spherical Projection.
We next come to a further very interesting fact
about crystals. Let us imagine a crystal, on which
the faces are fairly evenly developed, to be placed in
the middle of a sphere of jelly, as indicated in Fig. 47
(reproduced from a Memoir by the late Prof. Penfield),
so that the centre or origin of the axial system
of the crystal and the centre of the sphere coincide.
Let us now further imagine that long needles are
62stuck through the jelly and the crystal, one perpendicular
to each crystal face, and so as to reach the
centre. The crystal represented in Fig. 47 is a combination
of the cube a, octahedron o, and rhombic dodecahedron
d. If such a thing as we have imagined were
possible, we should find that the needles would emerge
at the surface of the sphere in points which would
lie on great circles, that is, on circles which represent
the intersection of
the sphere by
planes passing
through the centre.
Moreover, the
points would be
distributed along
these circles at
regularly recurring
angular positions,
corresponding to
the symmetry of
the crystal. If
the crystal belonged
to one of the
higher systems of symmetry, it would happen that
four of the points on at least one of these great
circles, and possibly on three of them, would be 90°
apart, that is, would be at the ends of rectangular
diameters, which would most likely be the axes of
reference. The other points would be distributed
symmetrically on each side of these four points.
The great circles on which the points are thus
symmetrically distributed—and they may legitimately
be taken to represent the faces, for tangent
63planes to the sphere at these points would be
parallel to the faces—are known as “zone circles,”
and the faces represented by the points on any one
of them form a “zone.” Now a zone of faces has
this practical property, that when the crystal is
supported so as to be rotatable about the zone
axis—which is parallel to the edges of intersection
of all the faces composing the zone, and is the normal
to the plane of the great circle representing the
zone—and a telescope is directed towards the
crystal perpendicularly to the zone axis, while a
bright object such as an illuminated slit is arranged
conveniently so as to be reflected from any face of
the crystal into the telescope, an image of it being
thus visible in the latter, then it will be found that
on rotating the crystal a similar image will be seen
reflected in the telescope from every face of the zone
in turn. Moreover, when the crystal is mounted on
a graduated circle, the angle of rotation between
the positions of adjustment to the cross-wires of
the telescope of any two successive images, reflected
from adjacent faces of the crystal, is actually the
angle between the two points representing the
faces concerned on the zone circle, and is the
supplement of the internal dihedral angle between
the two crystal faces themselves. It is, in fact,
the angle between the normals (perpendiculars) to
the two faces, the angle which is measured on the
goniometer.
This is, indeed, the very simple principle of the
reflecting goniometer, invented by Wollaston in
the year 1809, and which in its modern improved
form is the all-important principal instrument of
64the crystallographer’s laboratory. The work with
it consists largely in the measurement of the angles
between the faces in all the principal zones developed
on the crystal. The very fact, however,
that crystal faces occur so absolutely accurately
in zones immeasurably lightens the labours of the
crystallographer, and is one of prime importance.

Fig. 48.—The Reflecting Goniometer.
The most accurate and convenient modern form
of reflecting goniometer, reading to half-minutes
of arc, and provided with a delicate adjusting
apparatus for the crystal, is shown in Fig. 48. It
is constructed by Fuess of Berlin.
The graduated circle a is horizontal and is divided
directly to 15′, the verniers enabling the readings
65to be carried further either to single minutes, which
is all that is usually necessary, or to half-minutes in
the cases of very perfect crystals. The divided circle
is rotated by means of the ring b situated below,
and the reading of the verniers is accomplished
with the aid of the microscopes c. The circle which
carries the verniers is not fixed, except when this
is done deliberately by means of the clamping screw
d, but rotates with the telescope e to which it is
rigidly attached by means of an arm and a column
f. A fine adjustment is provided with the clamping
arrangement, so that the telescope can be adjusted
delicately with respect to the divided circle. Both
telescope and collimator are rigidly fixed at about
120° from each other during the actual measurements.
The collimator g is carried on a column h definitely
fixed to one of the legs (the back one in Fig. 48) of
the main basal tripod of the instrument. The
signal slit of the collimator is carried at the focus
of the objective about the middle of the tube g,
the outer half of the latter being an illumination
tube carrying a condensing lens to concentrate the
rays of light from the goniometer lamp on the slit.
The latter is not of the usual rectilinear character,
but composed of two circular-arc jaws, so that,
while narrow in the middle part like an ordinary
spectroscope slit, it is much broader at the two
ends in order to be much more readily visible; the
central part is narrow in order to enable fine adjustment
to the vertical cross-wire of the telescope to be
readily and accurately carried out. The shape of this
signal-slit will be gathered from the images of the slit
shown in Fig. 61 (page 126) in Chapter X. The telescope
66carries an additional lens k at its inner, objective,
end, in order that when this lens is rotated into
position the telescope may be converted into a low power
microscope for viewing the crystal and thus
enabling its adjustment to be readily carried out.
The crystal l is mounted on a little cone of goniometer
wax (a mixture of pitch and beeswax) carried
by the crystal holder. The latter fits in the top
of the adjusting movements, which consist of a
pair of rectangularly arranged centring motions,
and a pair of cylindrical adjusting movements;
the milled-headed manipulating centring screws
of the former are indicated by the letters m and n
in Fig. 48, and those which move the adjusting
segments are marked o and p. The top screw fixes
the crystal holder.
The crystal on its adjusting apparatus can be
raised or lowered to the proper height, level with
the axes of the telescope and collimator, by means
of a milled head at the base of the instrument,
there being an inner crystal axis moving (vertically
only) independently of the circle. Moreover, a
second axis outside this enables the crystal to be
rotated independently of the circle, the conical
axis of which is outside this again. The two can
be locked together when desired, however, by a
clamping screw provided with a fine adjustment q.
Freedom of movement of the crystal axis, unimpeded
by the weight of the circle, is thus permitted for
all adjusting purposes, the circle being only brought
into play when measurement is actually to occur.
With this instrument the most accurate work can
be readily carried out, and for ease of manipulation
67and general convenience it is the best goniometer
yet constructed.
The idea of regarding the centre of the crystal
as the centre of a sphere, within which the crystal
is placed (Fig. 47, page 62), gives crystallographers a
very convenient method of graphically representing a
crystal on paper, by projecting the sphere on to the
flat surface of the paper, the eye being supposed to be
placed at either the north or south pole of the sphere,
and the plane of projection to be that of the equatorial
great circle. The faces in the upper hemisphere
are represented by dots which are technically known
as the “poles” of the faces, corresponding to the
points where the needles normal to the faces emerge
from the imaginary globe, and all these points or
poles lie on a few arcs of great circles, which appear
in the projection either also as circular arcs terminating
at diametrically opposite points on the circumference
of the equatorial circle, which forms the
outer boundary of the figure and is termed the
“primitive circle,” or else, when the planes of the
great circles are at right angles to the equatorial
primitive circle, they appear as diametral straight
lines passing through the centre of the primitive
circle.
Such a stereographic projection offers a comprehensive
plan of the whole of the crystal faces,
which at once informs us of the symmetry in all
cases other than very complicated ones. A typical
one, that of the rhombic crystal of topaz shown in
Fig. 22 (page 40), is given in Fig. 49.
It will happen in all cases of higher symmetry,
as in that of topaz, for instance, that the poles in
68the lower hemisphere will project into the same
points as those representing the faces in the upper
hemisphere; but in cases of lower symmetry,
where they are differently situated, they are usually
represented by miniature rings instead of dots.
From the interfacial angles measured on the goniometer
the relative lengths and angular inclinations
(if other than 90°) of the crystal axes can readily
be calculated, by means of the simple formulæ
of spherical trigonometry; and the stereographic
projection constructed from the measurements as
just described proves an inestimable aid to these
calculations, by affording a comprehensive diagram
of all the spherical triangles required in making the
calculations.

Fig. 49.—Stereographic Projection of Topaz.
The relative axial lengths a : b : c (in which b is
always arranged to be = 1), and the axial angles α
(between b and c), β (between a and c), and γ (between
69a and b), form the “elements” of a crystal. These,
together with a list of the “forms” observed, and a
table of the interfacial angles, define the morphology
of the crystal, and are included in every satisfactory
description of a crystallographic investigation. They
are preceded by a statement of the name and chemical
composition and formula of the substance, the system
and the class of symmetry, and the habit or various
habits developed by crystals from a considerable
number of crops. An example of the mode of setting
out such a description will be found on pages 157
to 160.
Having thus made ourselves acquainted with the
real nature of the distribution of faces on a crystal,
and learnt how the crystallographer measures the
angles between the faces by means of the reflecting
goniometer, plots them out graphically on a stereographic
projection, and calculates therefrom the
“elements” of the crystal, it will be convenient again
to take up the historical development of the subject
so far as it relates to crystal forms and angles, and
their bearing on the chemical composition of the
substance composing the crystal, by introducing the
reader to the great work of Mitscherlich, whose
influence in the domain of chemical crystallography
was as profound as that of Haüy proved to be as
regards structural crystallography.
70
CHAPTER VII
THE WORK OF EILHARDT MITSCHERLICH AND HIS DISCOVERY OF ISOMORPHISM.
During the height of the French Revolution, which
caused the work of the Abbe Haüy to be suspended
for a time, although he was fortunately not one of
the many scientific victims of that terrible period,
there was born, on the 7th of January 1794, in the
village of Neuende, near Jever, in Oldenburg, the
man who was destined to continue that work on
its chemical side. Eilhardt Mitscherlich was the
son of the village pastor, and nephew of the celebrated
philologer, Prof. Mitscherlich of Göttingen.
His uncle’s influence appears to have given young
Mitscherlich a leaning towards philological studies,
for during his later terms at the Gymnasium at
Jever, where he received his early education, he
devoted himself with great energy to the study of
history and languages, for which he had a marked
talent, under the able direction and kind solicitude
of the head of the Gymnasium at that time, the
historian Schlosser. He eventually specialised on
the Persian language, and when Schlosser was
promoted to Frankfort young Mitscherlich accompanied
him, and there prosecuted these favourite
studies until the year 1811, when he went to the
university of Heidelberg.
71For some time now he had cherished the hope of
proceeding to Persia and conducting philological
investigations on the spot, and in 1813, an opportunity
presenting itself in the prospect of an embassy
being despatched to Persia by Napoleon, he transferred
himself to the university of Paris, with the
object of obtaining permission from Napoleon to
accompany the embassy. This visit to Paris must
have been one of Mitscherlich’s most exciting and
interesting experiences. For Napoleon had just
returned from the disastrous Russian campaign of
1812, and was feverishly engaged in raising a new
army wherewith to stem the great rise of the people
which was now re-awakening patriotic spirit throughout
the whole of Germany, and which threatened to
sweep away, as it eventually did, the huge fabric
of his central European Empire.
Indeed Mitscherlich appears to have been detained
in Paris during the exciting years 1813 and
1814, and with the abdication of Napoleon on April
4th of that year, he was obliged to give up all
idea of proceeding to Persia. He decided that the
only way of accomplishing his purpose was to
attempt to travel thither as a doctor of medicine.
He therefore returned to his native Germany
during the summer of 1814, and proceeded to
Göttingen, which was then famous for its medical
school. Here he worked hard at the preliminary
science subjects necessary for the medical degree,
while still continuing his philology to such serious
purpose as to enable him to publish, in 1815, the
first volume of a history of the Ghurides and Kara-Chitayens,
entitled “Mirchondi historia Thaheridarum.”
72It is obvious from the sequel, however,
that he very soon began to take much more than
a merely passing interest in his scientific studies,
and he eventually became so fascinated by them,
and particularly chemistry, as to abandon altogether
his cherished idea of a visit to Persia. Europe was
now settling down after the stormy period of the
hundred days which succeeded Napoleon’s escape
from Elba, terminating in his final overthrow on
June 18th, 1815, at Waterloo, and Mitscherlich was
able to devote himself to the uninterrupted prosecution
of the scientific work now opening before him.
He had the inestimable advantage of bringing to
it a culture and a literary mind of quite an unusually
broad and original character; and if the fall
of Napoleon brought with it the loss to the world
of an accomplished philologist, it brought also an
ample compensation in conferring upon it one of
the most erudite and broad-minded of scientists.
In 1818 Mitscherlich went to Berlin, and worked
hard at chemistry in the university laboratory
under Link. It was about the close of this year
or the beginning of 1819 that he commenced his
first research, and it proved to be one which will
ever be memorable in the annals both of chemistry
and of crystallography. He had undertaken the
investigation of the phosphates and arsenates, and
his results confirmed the conclusions which had
just been published by Berzelius, then the greatest
chemist of the day, namely, that the anhydrides of
phosphoric and arsenic acids each contain five
equivalents of oxygen, while those of the lower
phosphorous and arsenious acids contain only
73three. But while making preparations of the salts
of these acids, which they form when combined
with potash and ammonia, he observed a fact which
had escaped Berzelius, namely, that the phosphates
and arsenates of potassium and ammonium crystallise
in similar forms, the crystals being so like each
other, in fact, as to be indistinguishable on a merely
cursory inspection.
Being unacquainted with crystallography, and
perceiving the importance of the subject to the
chemist, he acted in a very practical and sensible
manner, which it is more than singular has not
been universally imitated by all chemists since
his time. He at once commenced the study of
crystallography, seeing the impossibility of further
real progress without a working knowledge of that
subject. He was fortunate in finding in Gustav
Rose, the Professor of Geology and Mineralogy at
Berlin, not merely a teacher close at hand, but also
eventually a life-long intimate friend. Mitscherlich
worked so hard under Rose that he was very soon
able to carry out the necessary crystal measurements
with his newly prepared phosphates and arsenates.
He first established the complete morphological
similarity of the acid phosphates and arsenates
of ammonium, those which have the composition
NH4H2PO4 and NH4H2AsO4 and crystallise in
primary tetragonal prisms terminated by the
primary pyramid faces; and then he endeavoured
to produce other salts of ammonia with other acids
which should likewise give crystals of similar form.
But he found this to be impossible, and that only
the phosphates and arsenates of ammonia exhibited
74the same crystalline forms, composed of faces
inclined at similar angles, which to Mitscherlich
at this time appeared to be identical. He next
tried the effect of combining phosphoric and arsenic
acids with other bases, and he found that potassium
gave salts which crystallised apparently exactly
like the ammonium salts.
He then discovered that not only do the acid
phosphates and arsenates of potassium and ammonium,
H2KPO4, H2(NH4)PO4, H2KAsO4, and
H2(NH4)AsO4 crystallise in similar tetragonal forms,
but also that the four neutral di-metallic salts of
the type HK2PO4 crystallise similarly to each other.
He came, therefore, to the conclusion that there
do exist bodies of dissimilar chemical composition
having the same crystalline form, but that these
substances are of similar constitution, in which one
element, or group of elements, may be exchanged
for another which appears to act analogously, such
as arsenic for phosphorus and the ammonium group
(although its true nature was not then determined)
for potassium. He observed that certain minerals
also appeared to conform to this rule, such as the
rhombohedral carbonates of the alkaline earths,
calcite CaCO3, dolomite CaMg(CO3)2, chalybite
FeCO3, and dialogite MnCO3; and the orthorhombic
sulphates of barium (barytes, BaSO4), strontium
(celestite, SrSO4), and lead (anglesite, PbSO4).
Wollaston, who, in the year 1809, had invented the
reflecting goniometer, and thereby placed a much
more powerful weapon of research in the hands of
crystallographers, had already, in 1812, shown this
to be a fact as regards the orthorhombic carbonates
75(witherite, strontianite, and cerussite) and sulphates
(barytes, celestite, and anglesite) of barium, strontium,
and lead, as the result of the first exact angular
measurements made with his new instrument; but
his observations had been almost ignored until
Mitscherlich reinstated them by his confirmatory
results.
While working under the direction of Rose,
Mitscherlich had become acquainted with the work
of Haüy, whose ideas were being very much discussed
about this time, Haüy himself taking a very
strong part in the discussion, being particularly
firm on the principle that every substance of definite
chemical composition is characterised by its own
specific crystalline form. Such a principle appeared
to be flatly contradicted by these first surprising
results of Mitscherlich, and it naturally appeared
desirable to the latter largely to extend his observations
to other salts of different groups. It was for
this reason that he had examined the orthorhombic
sulphates of barium, strontium, and lead, and the
rhombohedral carbonates of calcium, magnesium,
iron, and manganese, with the result already stated
that the members of each of these groups of salts
were found to exhibit the same crystalline form, a
fact as regards the former group of sulphates which
had already been pointed out not only by Wollaston
but by von Fuchs (who appears to have ignored
the work of Wollaston) in 1815, but had been
explained by him in a totally unsatisfactory
manner. Moreover, about the same time the
vitriols, the sulphates of zinc, iron, and copper,
had been investigated by Beudant, who had shown
76that under certain conditions mixed crystals of
these salts could be obtained; but Beudant omitted
to analyse his salts, and thus missed discovering
the all-important fact that the vitriols contain
water of crystallisation, and in different amounts
under normal conditions. Green vitriol, the
sulphate of ferrous iron, crystallises usually with
seven molecules of water of crystallisation, as
does also white vitriol, zinc sulphate; but blue
vitriol, copper sulphate, crystallises with only five
molecules of water under ordinary atmospheric
conditions of temperature and pressure. Moreover,
copper sulphate forms crystals which belong
to the triclinic system, while the sulphates of zinc
and iron are dimorphous, the common form of zinc
sulphate, ZnSO4.7H2O, being rhombic, like Epsom
salts, the sulphate of magnesia which also crystallises
with seven molecules of water, MgSO4.7H2O,
while that of ferrous sulphate, FeSO4.7H2O, is
monoclinic, facts which still further complicate
the crystallography of this group and which were
quite unknown to Beudant and were unobserved
by him. But Beudant showed that the addition of
fifteen per cent. of ferrous sulphate to zinc sulphate,
or nine per cent. to copper sulphate, caused
either zinc or copper sulphate to crystallise in the
same monoclinic form as ferrous sulphate. He also
showed that all three vitriols will crystallise in
mixed crystals with magnesium or nickel sulphates,
the ordinary form of the latter salt, NiSO4.7H2O,
being rhombic like that of Epsom salts.
The idea that two chemically distinct substances
not crystallising in the cubic system, where the high
77symmetry determines identity of form, can occur
in crystals of the same form, was most determinedly
combated by Haüy, and the lack of chemical
analyses in Beudant’s work, and the altogether
incorrect “vicarious” explanation given by von
Fuchs, gave Haüy very grave cause for suspicion
of the new ideas. The previous observations of
Rome de l’Isle in 1772, Le Blanc in 1784, Vauquelin
in 1797, and of Gay-Lussac in 1816, that the various
alums, potash alum, ammonia alum, and iron alum,
will grow together in mixed crystals or in overgrowths
of one crystal on another, when a crystal
of any one of them is hung up in the solution of
any other, does not affect the question, as the alums
crystallise in the cubic system, the angles of the
highly symmetric forms of which are absolutely
identical by virtue of the symmetry itself.
It was while this interesting discussion was
proceeding that Mitscherlich was at work in Berlin,
extending his first researches on the phosphates
and arsenates to the mineral sulphates and
carbonates. But he recognised, even thus early,
what has since become very clear, namely, that
owing to the possibility of the enclosure of impurities
and of admixture with isomorphous
analogues, minerals are not so suitable for investigation
in this regard as the crystals of artificially
prepared chemical salts. For the latter can be
prepared in the laboratory in a state of definitely
ascertained purity, and there is no chance of that
happening which Haüy was inclined to think was
the explanation of Mitscherlich’s results, namely,
that certain salts have such an immense power of
78crystallisation that a small proportion of them in
a solution of another salt may coerce the latter into
crystallisation in the form of that more powerfully
crystallising salt. Mitscherlich made a special study,
therefore, of the work of Beudant, and repeated the
latter observer’s experiments, bringing to the
research both his crystallographic experience and
that of a skilful analyst. He prepared the pure
sulphates of ferrous iron, copper, zinc, magnesium,
nickel and cobalt, all of which form excellent crystals.
He soon cleared up the mystery in which Beudant’s
work had left the subject, by showing that the
crystals contained water of crystallisation, and in
different amounts. He found what has since been
abundantly verified, that the sulphates of copper
and manganese crystallise in the triclinic system
with five molecules of water, CuSO4.5H2O and
MnSO4.5H2O; in the case of manganese sulphate,
however, this is only true when the temperature is
between 7° and 20°, for if lower than 7° rhombic
crystals of MnSO4.7H2O similar to those of the
magnesium sulphate group are deposited, and if
higher than 20° the crystals are tetragonal and
possess the composition MnSO4.4H2O. The Epsom
salts group crystallising in the rhombic system
with seven molecules of water consists of magnesium
sulphate itself, MgSO4.7H2O, zinc sulphate ZnSO4.7H2O,
and nickel sulphate NiSO4.7H2O. The third
group of Mitscherlich consists of sulphate of ferrous
iron FeSO4.7H2O and cobalt sulphate CoSO4.7H2O,
and both crystallise at ordinary temperatures
with seven molecules of water as indicated by the
formulæ, but in the monoclinic system. Thus two
79of the groups contain the same number of molecules
of water, yet crystallise differently. But Mitscherlich
next noticed a very singular fact, namely, that if
a crystal of a member of either of these two groups
be dropped into a saturated solution of a salt of
the other group, this latter salt will crystallise out
in the form of the group to which the stranger
crystal belongs. Hence he concluded that both
groups are capable of crystallising in two different
systems, rhombic and monoclinic, and that under
the ordinary circumstances of temperature and
pressure three of the salts form most readily the
rhombic crystals, while the other two take up
most easily the monoclinic form. Mitscherlich
then mixed the solutions of the different salts,
and found that the mixed crystals obtained presented
the form of some one of the salts employed.
Thus even so early in his work Mitscherlich indicated
the possibility of dimorphism. Moreover, before
the close of the year 1819 he had satisfied himself
that aragonite is a second distinct form of carbonate
of lime, crystallising in the rhombic system and quite
different from the ordinary rhombohedral form
calcite. Hence this was another undoubted case
of dimorphism.
During this same investigation in 1819, Mitscherlich
studied the effect produced by mixing the
solution of each one of the above-mentioned seven
sulphates of dyad-acting metals with the solution
of sulphate of potash, and made the very important
discovery that a double salt of definite composition
was produced, containing one equivalent of potassium
sulphate, one equivalent of the dyad sulphate
80(that of magnesium, zinc, iron, manganese, nickel,
cobalt, or copper), and six equivalents of water of
crystallisation, and that they all crystallised well
in similar forms belonging to the monoclinic system.
Some typical crystals of one of these salts, ammonium
magnesium sulphate, are illustrated in Fig. 30 (Plate
VII., facing page 44). This is probably the most
important series of double salts known to us, and is
the series which has formed the subject of prolonged
investigation on the part of the author, no less than
thirty-four different members of the series having
been studied crystallographically and physically since
the year 1893, and many other members still remain
to be studied. An account of this work is given in
a Monograph published in the year 1910 by Messrs
Macmillan & Co., and entitled, “Crystalline Structure
and Chemical Constitution.”
This remarkable record for a first research was
presented by Mitscherlich to the Berlin Academy
on the 9th December 1819. During the summer
of the same year Berzelius visited Berlin, and was
so struck with the abilities of Mitscherlich, then
twenty-five years old, that he persuaded him to
accompany him on his return to Stockholm, and
Mitscherlich continued his investigations there under
the eye of the great chemist. His first work at
Stockholm consisted of a more complete study of
the acid and neutral phosphates and arsenates of
potash, soda, ammonia, and lead. He showed
that in every case an arsenate crystallises in the
same form as the corresponding phosphate. Moreover,
in 1821 he demonstrated that sodium dihydrogen
phosphate, NaH2PO4, crystallises with a molecule
81of water of crystallisation in two different forms,
both belonging to the rhombic system but with
quite different axial ratios; this was consequently
a similar occurrence to that which he had observed
with the sulphates of the iron and zinc groups.
It was while Mitscherlich was in Stockholm that
Berzelius suggested to him that a name should be
given to the new discovery that analogous elements
can replace each other in their crystallised compounds
without any apparent change of crystalline
form. Mitscherlich, therefore, termed the phenomenon
“isomorphism,” from ἰσός, equal to,
and μορφή, shape. The term “isomorphous” thus
strictly means “equal shaped,” implying not only
similarity in the faces displayed, but also absolute
equality of the crystal angles. The fact that the
crystals of isomorphous substances are not absolutely
identical in form, but only very similar, was not likely
to be appreciated by Mitscherlich at this time. For
the reflecting goniometer had only been invented by
Wollaston in 1809, and accurate instruments reading
to minutes of arc were mechanical rarities. It will
be shown in the sequel, as the result of the author’s
investigations, that there are angular differences,
none the less real because relatively very small,
between the members of such series. But Mitscherlich
was not in the position to observe them.
It must be remembered, moreover, that he was
primarily a chemist, and that he had only acquired
sufficient crystallographic knowledge to enable him
to detect the system of symmetry, and the principal
forms (groups of faces having equal value as regards
the symmetry) developed on the crystals which
82he prepared. His doctrine of isomorphism, accepted
in this broad sense, proved of immediate and important
use in chemistry. For there were uncertainties
as to the equivalents of some of the
chemical elements, as tabulated by Berzelius, then
the greatest authority on the subject, and these
were at once cleared up by the application of the
principle of isomorphism.
The essence of Mitscherlich’s discovery was,
that the chemical nature of the elements present
in a compound influences the crystalline form by
determining the number and the arrangement of
the atoms in the molecule of the compound; so
that elements having similar properties, such for
instance as barium, strontium, and calcium, or
phosphorus and arsenic, combine with other elements
to form similarly constituted compounds,
both as regards number of atoms and their arrangement
in the molecule. Number of atoms alone,
however, is no criterion, for the five atoms of the
ammonium group NH4 replace the one atom of
potassium without change of form.
This case of the base ammonia had been one of
Mitscherlich’s greatest difficulties during the earlier
part of his work, and remained a complete puzzle
until about this time, when its true chemical
character was revealed. For until the year 1820
Berzelius believed that it contained oxygen. Seebeck
and Berzelius had independently discovered
ammonium amalgam in 1808, and Davy found, on repeating
the experiment, that a piece of sal-ammoniac
moistened with water produced the amalgam with
mercury just as well as strong aqueous ammonia.
83Both Berzelius and Davy came to the conclusion
that ammonia contains oxygen, like potash and
soda, and that a metallic kind of substance resembling
the alkali metals, potassium and sodium, was
isolated from this oxide or hydrate by the action
of the electric current, which Seebeck had shown
facilitated the formation of the so-called ammonium
amalgam. Davy, however, accepted in part the
views of Gay-Lussac and Thénard, who, in 1809,
concluded from their experiments that ammonium
consisted of ammonia gas NH3 with an additional
atom of hydrogen, the group NH4 then acting like
an alkali metal, views which time has substantiated.
But their further erroneous conclusion that sodium
and potassium also contained hydrogen was rejected
by him. Berzelius, however, set his face both
against this latter fallacy and the really correct
NH4 theory, and it was not until four years after
Ampère, in 1816, had shown that sal-ammoniac
was, in fact, the compound of the group NH4 with
chlorine, that Berzelius, about the year 1820, after
thoroughly sifting the work of Ampère, accepted
the view of the latter that in the ammonium salts
it is the group NH4, acting as a radicle capable of
replacing the alkali metals, which is present.
The fact that this occurred at this precise moment,
four years after the publication of Ampère’s results,
leads to the conclusion that the observation of
Mitscherlich, that the ammonium compounds are
isomorphous with the potassium compounds, was
the compelling argument which caused Berzelius
finally to admit what has since proved to be the
truth.
84While still at Stockholm Mitscherlich showed
that the chromates and manganates are isomorphous
with the sulphates, and also that the perchlorates
and permanganates are isomorphous with each
other. Although these facts could not be properly
explained at the time, owing to the inadequate
progress of the chemistry of manganese, it was
seen that potassium chromate, K2CrO4, contained
the same number of atoms as potassium sulphate,
K2SO4, and that potassium permanganate KMnO4
and perchlorate KClO4 likewise resembled each
other in regard to the number of atoms contained
in the molecule.
As a good instance of the use of the principle
of isomorphism, we may recall that when Marignac,
in 1864, found himself in great difficulty about the
atomic weights of the little known metals tantalum
and niobium which he was investigating, he discovered
that their compounds are isomorphous;
the pentoxides of the two metals occur together
in isomorphous mixture in several minerals, and
the double fluorides with potassium fluoride,
K2TaF7 and K2NbF7 are readily obtained in crystals
of the same form. The specific heat of tantalum
was then unknown, so that the law of Dulong and
Petit connecting specific heat with atomic weight
could not be applied, and the vapour density of
tantalum chloride, as first determined by Deville
and Troost with impure material, did not indicate
an atomic weight for tantalum which would give it
the position among the elements that the chemical
reactions of the metal indicated. Yet Marignac
was able definitely to decide, some time before the
85final vapour density determinations of Deville and
Troost with pure salts, from the fact of the isomorphism
of their compounds, that the only possible
positions for tantalum and niobium were such as
corresponded with the atomic weights 180 and
93 respectively. Time has only confirmed this
decision, and we now know that niobium and
tantalum belong to the same family group of
elements as that to which vanadium belongs, and
the only difference which modern research has introduced
has been to correct the decimal places of the
atomic weights, that of niobium (now also called
columbium, the name given to it by its discoverer,
Hatchett, in 1801) being now accepted as 92.8 and
that of tantalum 179.6, when that of hydrogen = 1.
Applying the law of isomorphism in a similar
manner, Berzelius was enabled to fix the atomic
weights of copper, cadmium, zinc, nickel, cobalt,
iron, manganese, chromium, sulphur, selenium,
and chlorine, the numbers accepted to-day differing
only in the decimal places, in accordance with the
more accurate results acquired by the advance of
experimental and quantitative analytical methods.
But with regard to several other elements, owing
to inadequate data, Berzelius made serious mistakes,
showing how very great is the necessity for care
and for ample experimental data and accurate
measurements, before the principle of isomorphism
can be applied with safety. Given these, and we
have one of the most valuable of all the aids known
to us in choosing the correct atomic weight of
an element from among two or three possible
alternatives. We are only on absolutely sure
86ground when we are dealing not only with a series
of compounds consisting of the same number of
atoms, but when also the interchangeable elements
are the intimately related members of a family
group, such as we have since become familiar with
in the vertical groups of elements in the periodic
table of Mendeléeff.
Before leaving Stockholm Mitscherlich showed,
from experiments on the crystallisation of mixtures
of the different sulphates with which he had been
working, that isomorphous substances intermix
in crystals in all proportions, and that they also
replace one another in minerals in indefinite proportions,
a fact which has of recent years been
wonderfully exemplified in the cases of the hornblende
(amphibole) and augite (pyroxene) groups.
In November 1821 Mitscherlich closed these
memorable labours at Stockholm and returned to
Berlin, where he acted as extraordinary professor
of the university until 1825, when he was elected
professor in ordinary. His investigations for a
time were largely connected with minerals, but on
July 6th, 1826, he presented a further most important
crystallographic paper to the Berlin Academy, in
which he announced his discovery of the fact that
one of the best known chemical elements, sulphur,
is capable of crystallising in two distinct forms.
The ordinary crystals found about Etna and
Vesuvius and in other volcanic regions agree with
those deposited from solution in carbon bisulphide
in exhibiting rhombic symmetry. But Mitscherlich
found that when sulphur is fused and allowed to
cool until partially solidified, and the still liquid
87portion is then poured out of the crucible, the walls
of the latter are found to be lined with long monoclinic
prisms. These have already been illustrated
in Fig. 2, Plate I., in Chapter I.
Here was a perfectly clear case of an element—not
liable to any charge of difference of chemical
composition such as might have applied to the cases
of sodium dihydrogen phosphate, carbonate of
lime, and iron vitriol and its analogues, which he
had previously described as cases of the same
substance crystallising in two different forms—which
could be made to crystallise in two different
systems of symmetry at will, by merely changing
the circumstances under which the crystallisation
occurred. His explanation being thus proved
absolutely, he no longer hesitated, but at once
applied the term “dimorphous” to these substances
exhibiting two different forms, and referred to the
phenomenon itself as “dimorphism.” The case
of carbonate of lime had given rise to prolonged
discussion, for the second variety, the rhombic
aragonite, had been erroneously explained by
Stromeyer, after Mitscherlich’s first announcement
in 1819, as being due to its containing strontia as
well as lime, and the controversy raged until
Buchholz discovered a specimen of aragonite which
was absolutely pure calcium carbonate, so that
Mitscherlich’s dimorphous explanation was fully
substantiated.
Dimorphism is very beautifully illustrated by
the case of the trioxide of antimony, Sb2O3, a slide
of which, obtained by sublimation of the oxide
from a heated tube on to the cool surface of a glass
88microscope slip, is seen reproduced in Fig. 50, Plate XI.
The two forms are respectively rhombic and cubic.
The rhombic variety usually takes the form of long
needle-shaped crystals, which are shown in Fig. 50
radiating across the field and interlacing with one
another; the cubic variety crystallises in octahedra, of
which several are shown in the illustration, perched
on the needles, one interesting individual being poised
on the end of one of the needles. The two forms
occur also in nature as the rhombic mineral valentinite
and the cubic mineral senarmontite, which
latter crystallises in excellent regular octahedra.
Antimonious oxide, moreover, is not only isomorphous,
but isodimorphous with arsenious oxide,
a slide of octahedra of which has already been reproduced
in Fig. 3, Plate I., in Chapter I. For besides
this common octahedral form of As2O3 artificial
crystals of arsenious oxide have been prepared of
rhombic symmetry, resembling valentinite. Hence
the two lower oxides of arsenic and antimony afford
us a striking case of the simultaneous display of
Mitscherlich’s two principles of isomorphism and
dimorphism.
Thus the position in 1826 was that Mitscherlich
had discovered the principle of isomorphism, and
had also shown the occurrence of dimorphism in
several well-proved specific cases, and that he
regarded at this time isomorphism as being a literal
reality, absolute identity of form.
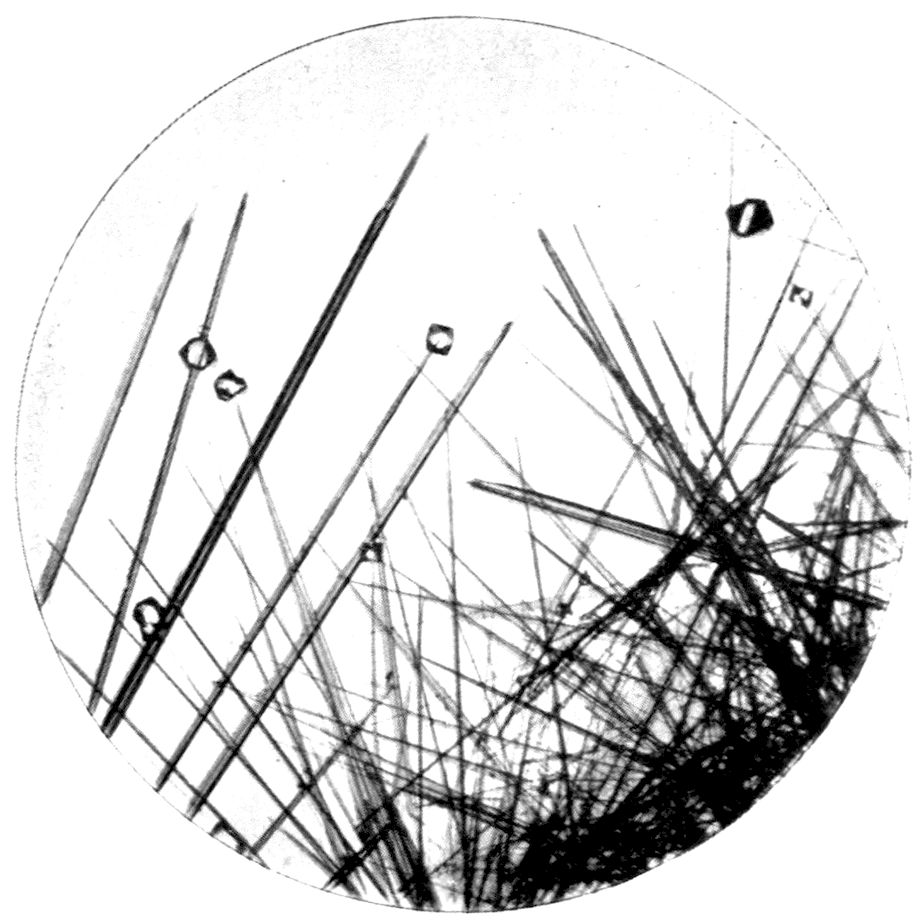
PLATE XI.
Fig. 50.—Rhombic Needles and Cubic Octahedra of Antimony Trioxide obtained by Sublimation. An interesting Example of Dimorphism.

Fig. 101.—Ammonium Chloride crystallising· from a Labile Supersaturated Solution (see p. 248).
Reproductions of Photomicrographs.
89These striking results appeared at once to demolish
the theory that any one substance of definite
chemical composition is characterised by a specific
crystalline form, which was Haüy’s most important generalisation. Mitscherlich, however, soon
expressed doubts as to the absolute identity of
form of his isomorphous crystals, and saw that it was
quite possible that in the systems other than
the cubic (in which latter system the highly
perfect symmetry itself determines the form, and
that the angles shall be identically constant),
there might be slight distinctive differences in the
crystal angles. For he caused to be constructed,
by the celebrated optician and mechanician, Pistor,
the most accurate goniometer which had up till
then been seen, provided with four verniers, each
reading to ten seconds of arc, and with a telescope
magnifying twenty times, for viewing the reflections
of a signal, carried by a collimator, from the crystal
faces. Unfortunately in one respect, he was almost
at once diverted, by the very excess of refinement
of this instrument, to the question of the alteration
of the crystal angles by change of temperature,
and lost the opportunity, never to recur, of doing
that which would at once have reconciled his views
with those of Haüy in regard to this important
matter, namely, the determination of these small
but real differences in the crystal angles of the
different members of isomorphous series, and the
discovery of the interesting law which governs them,
a task which in these later days has fallen to the lot
of the author.
Another remarkable piece of crystallographic
work, this time in the optical domain, which has
rendered the name of Mitscherlich familiar, was his
discovery of the phenomenon of crossed-axial-plane
dispersion of the optic axes in gypsum. (The nature
90and meaning of “optic axes” will be explained in
Chapter XIII., page 185.) During the course of a
lecture to the Berlin Academy in the year 1826 Mitscherlich,
always a brilliant lecturer and experimenter
at the lecture table, exhibited an experiment with
a crystal of gypsum (selenite) which has ever since
been referred to as the “Mitscherlich experiment.”
He had been investigating the double refraction
of a number of crystalline substances at different
temperatures, and had observed that gypsum,
hydrated calcium sulphate, CaSO4.2H2O, was
highly sensitive in this respect, especially as regards
the position of its optic axes. At the ordinary
temperature it is biaxial, with an optic axial angle
of about 60°, but on heating the crystal the angle
diminishes, until just above the temperature of
boiling water the axes become identical, as if the
crystal were uniaxial, and then they again separate
as the temperature rises further, but in the plane
at right angles to that which formerly contained
them; hence the phenomenon is spoken of as
“crossed-axial-plane dispersion.” Mitscherlich
employed a plate of the crystal cut perpendicularly
to the bisectrix of the optic axial angle, and
showed to the Academy the interference figures
(see Plate XII.) which it afforded in convergent
polarised light with rising temperature. At first,
for the ordinary temperature, the usual rings and
lemniscates surrounding the two optic axes were
apparent at the right and left margins of the field;
as the crystal was gently heated (its supporting
metallic frame being heated with a spirit lamp)
the axes approached each other, with ever changing
91play of colour and alteration of shape of the rings
and lemniscates, until eventually the dark hyperbolic
brushes, marking by their well defined vertices
the positions of the two optic axes within the innermost
rings, united in the centre of the field to produce
the uniaxial dark rectangular cross; the
rings around the centre had now become circles, the
lemniscates having first become ellipses which
more and more approximated, as the temperature
rose, to circles. Then the dark cross opened out
again, and the axial brushes separated once more,
but in the vertical direction, and the circles became
again first ellipses and then lemniscates, eventually
developing inner rings around the optic axes; if
the source of heat were not removed at this stage
the crystal would suddenly decompose, becoming
dehydrated, and the field on the screen would
become dark. If, however, the spirit lamp were
removed before this occurred, the phenomena were
repeated in the reverse order as the crystal cooled.
This beautiful experiment is now frequently
performed, as gypsum is perhaps the best example
yet known which exhibits the phenomenon of
crossed-axial-plane dispersion by change of temperature
alone. A considerable number of other
cases are known, such as brookite, the rhombic
form of titanium dioxide TiO2, and the triple tartrate
of potassium, sodium, and ammonium, but these
are more sensitive to change of wave-length in the
illuminating light than to change of temperature.
92

Fig. 51.—The Mitscherlich Experiment with Gypsum.

PLATE XII.
Fig. 52.—Appearance of the Interference Figure half a Minute after commencing the Experiment. Temperature of Crystal about 40° C.

Fig. 53.—Appearance a Minute or so later, the Axes approaching the Centre. Temperature of Crystal about 85° C.

Fig. 54.—The Two Optic Axes coincident in the Centre of the Figure, two or three Minutes from the commencement. Temperature of Crystal 106° C.

Fig. 55.—The Axes re-separated in the Vertical Plane a Minute or two later. Temperature of Crystal about 125° C.
The Mitscherlich Experiment with Gypsum.
Four Stages in the Transformation of the Interference Figure in Convergent Polarised Light, from Horizontally Biaxial through Uniaxial to Vertically Biaxial, on Raising the Temperature To 125° C.
(From Photographs by the author.)
93The author has recently exhibited the “Mitscherlich
experiment” to the Royal Society,[2] and
also in his Evening Discourse to the British Association
at their 1909 meeting in Winnipeg, in a new
and more elegant manner, employing the large Nicolprism
projection polariscope shown in Fig. 51,
and a special arrangement of lenses for the convergence
of the light, which is so effective that no
extraneous heating of the crystal is required. The
convergence of the rays is so true on a single spot
in the centre of the crystal plate about two millimetres
diameter, that a crystal plate not exceeding
6 mm. is of adequate size, mounted in a miniature
holder-frame of platinum or brass with an aperture
not more than 3 mm; the thickness of the crystal
should remain about 2 mm., in order that the
rings round the axes may not be too large and
diffuse, the crystal being endowed with very feeble
double refraction, which is one of the causes of the
phenomenon. Such a small crystal heats up so
rapidly in the heat rays accompanying the converging
light rays—even with the essential cold
water cell two inches thick between the lantern
condenser and the polarising Nicol, for the protection
of the balsam of the latter—that any extraneous
heating by a spirit or other lamp is entirely
unnecessary. The moment the electric arc of the
lantern is switched on, the optic axial rings appear
at the right and left margins of the screen, when the
crystal is properly adjusted and the arc correctly
centred, and they march rapidly to the crossing
point in the centre, where the dark hyperbolæ
unite to produce the rectangular St Andrew’s cross,
the rings, figure-eight curves, and other lemniscates
passing through the most exquisite evolutions
and colour changes all the time until they form the
circular Newton’s rings, around the centre of the
cross; after this the cross and circles again open
out, but along the vertical diameter of the screen,
into hyperbolæ and rings and loop-like lemniscates
surrounding two axes once more. It is wise
as soon as the separation in this plane is complete
and the first or second separate rings have appeared
round the axes, to arrest the heating by merely
interposing intermittently a hand screen between
the lantern and polariser, or by blowing a current
of cool air past the crystal, which will cause
the axes to recede again, and the phenomena
to be reversed, the crossing point being repassed, and
the axes brought into the original horizontal plane
again. By manipulation of the screen, or air-current,
94the axes can thus be caused to approach or to recede
from the centre at will, along either the horizontal
or vertical diameter. Four characteristic stages of
the experiment are shown in Figs. 52 to 55, Plate XII.
Fig. 52 exhibits the appearance just after commencing
the experiment, the optic axes being well in the
field of view. Fig. 53 shows the axes horizontally
approaching the centre. Fig. 54 shows the actual
crossing, which occurs for different crystals at
temperatures varying from 105°.5 to 111°.5 C.; and
Fig. 55 represents the axes again separated, but
vertically.
The experiment as thus performed is one of the
most beautiful imaginable, and it can readily be
understood how delighted were Mitscherlich’s
audience on the occasion of its first performance
by him. The author has since discovered no less
than six other cases of substances which exhibit
crossed-axial-plane dispersion of the optic axes, in the
course of his investigations, one of which is illustrated
in Plate XIII., facing page 108; and, moreover,
has arrived at a general explanation of the whole
phenomenon, the main points of which are that
such substances, besides showing very feeble double
refraction (the two extreme of the three refractive
indices being very close together), also exhibit
very close approximation of the intermediate
refractive index β to either the minimum index
α or the maximum index γ. Also, change of
temperature, or of wave-length, or most usually
both, must so operate as to bring the two indices
closest together into actual identity and then to
pass beyond each other, these two indices thus
95exchanging positions, the extreme one becoming
the intermediate index. In other words, the
uniaxial cross and circular rings are produced
owing to two of the three refractive indices (corresponding
to the directions of the three rectangular
axes of the ellipsoid which, in general, expresses
the optical properties of a crystal) becoming
equal at the particular temperature at which the
phenomenon is observed to occur, and for light
of the specific wave-length in question. The ellipsoid
of general form which represents the optical
properties of a biaxial crystal thus becomes converted
into a rotation ellipsoid corresponding to a uniaxial
crystal. Brookite and the triple tartrate are
excellent examples of the predominance of the
effect of change of wave-length, for the optic axes
are separated in both cases widely in one plane for
red light and almost equally widely in the perpendicular
plane for blue light. The new cases
observed by the author are sensitive both to change
of wave-length and to change of temperature, and so
fall midway between the cases just quoted and the
case of gypsum. The cause of it, in four of these new
instances, is a very interesting one, connected with
the regular change of the refractive indices in accordance
with the law of progression in an isomorphous
series according to the atomic weight of the alkali
metal present, which will be discussed in Chapter X.
A further most important discovery was made
by Mitscherlich in the year 1827, which also profoundly
concerns the work of the author, namely,
that of selenic acid, H2SeO4, analogous to sulphuric
acid, and of the large group of salts derived from
96it, the selenates, analogous to the sulphates. He
showed first that potassium selenate, K2SeO4, is
isomorphous with potassium sulphate, K2SO4, and
subsequently that the selenates in general are
isomorphous with the corresponding sulphates;
consequently it followed that selenium is a member
of the sulphur family of elements. This element
selenium had only been discovered ten years
previously by his friend Berzelius, and doubtless
Mitscherlich had seen a great deal of the work in
connection with it during the two years which he
spent in the laboratory of Berzelius at Stockholm,
and was deeply interested in it.
The discovery has proved a most fruitful one,
for the selenates are beautifully crystalline salts,
particularly suitable for crystallographic researches,
and their detailed investigation has afforded a
most valuable independent confirmation of the
important results obtained for the sulphates.
Again in 1830 Mitscherlich, following up the
preliminary work already referred to, definitely
established another fact bearing on the same series,
namely, the isomorphism of potassium manganate
K2MnO4 with the sulphate and selenate of potash;
moreover, on continuing his study of the manganese
salts he further substantiated the isomorphism of
the permanganates with the perchlorates, and isolated
permanganic acid. This also proved a most important
step forward, as these salts likewise afford admirable
material for crystallographic investigation, and
such an examination, carried out by Muthmann and
Barker, has yielded most valuable results.
Much later in his career Mitscherlich also
97described the dimorphous iodide of mercury,
HgI2, one of the most remarkable and interesting
salts known to us, the unstable yellow rhombic
modification being converted into the more stable
red tetragonal form by merely touching with
a hard substance. Also we are indebted to him
at the same later period for our knowledge of the
crystalline forms of the elements phosphorus,
iodine, and selenium, when crystallised from solution
in bisulphide of carbon.
From the record of achievements which has now
been given in this chapter it will be obvious how
much chemical crystallography owes to Mitscherlich.
The description of his work has taken us into almost
every branch of the subject, morphological, optical,
and thermal, and although it has consequently
been necessary to refer to phenomena which have
not yet been explained in this book, it has doubtless
proved on the whole most advantageous thus to
present the life work of this great master as a
complete connected story.
98
CHAPTER VIII
MORPHOTROPY AS DISTINCT FROM ISOMORPHISM.
It has been shown in the last chapter how Mitscherlich
discovered the principle of isomorphism,
as applying to the cases of substances so closely
related that their interchangeable chemical elements
are members of the same family group; and also
how the principle enabled him to determine the
chemical constitution of two hitherto unknown
acids which he isolated, selenic H2SeO4 and permanganic
HMnO4. For he observed that the
selenates were isomorphous with the sulphates,
and the permanganates with the perchlorates.
It was further made clear that the principle as
bequeathed to us by Mitscherlich was only defined
in very general terms, and its details have only
recently been precisely decided.
Before proceeding further (in Chapter X.) with the
elucidation of the true nature of isomorphism,
however, some important crystallographic relationships
between substances less closely related than
family analogues must be referred to, as the outcome
of a series of investigations by von Groth,
chiefly between the derivatives of the hydrocarbon
benzene. Also, some suggestive results obtained
by the author from an investigation of an organic
homologous series, that is, one the members of
99which differ by the regular addition of a CH3 group,
may be briefly referred to.
The interval between the work of Mitscherlich
and that of von Groth was one of doubt, discouragement,
and somewhat of discredit for chemical
crystallography. The chemists Laurent[3] and
Nicklès[4] carried out during the years from 1842
to 1849 measurements of numerous organic substances
and of some inorganic compounds, the
former chiefly halogen or other derivatives of
particular hydrocarbons or salts of homologous
fatty acids. Laurent, for instance, found that
naphthalene tetrachloride, C10H8.Cl4, and chloronaphthalene
tetrachloride, C10H7Cl.Cl4, crystallise in
different systems, the former in the monoclinic
and the latter in the rhombic system. Yet the
primary prism angles of the two are less than a
degree different, namely, 109° 0′ and 109° 45′.
Laurent named this kind of similarity “hemimorphism,”
a most unfortunate term as it was
already employed in crystallography in its other
well-known geometrical significance, that is, to
denote a crystal differently terminated at the two
ends of an axis. Many other like similarities were
discovered by Laurent, and he again coined an
objectionable term, now discarded, to represent the
cases of similarity extending over more than the
same system, namely, “isomeromorphism.”
Nicklès observed similar facts in connection
with the barium salts of the fatty acids, which
crystallise in different systems with different
100amounts of water of crystallisation. But their
prism angles are all within a couple of degrees of
each other, varying from 98° to 100°. Thus the
phenomenon of “isogonism,” a term much less objectionable
than those invented by Laurent, appears to
be a common observance not only for different kinds
of derivatives of the same original hydrocarbon or
other organic nucleus, but also for the case of
homologous series. But Nicklès missed the real
point by including salts with different amounts of
water, which, it will be shown later, entirely upset
the crystalline structure. When this is eliminated
the resemblance between true similarly constituted
homologues, differing by regular increments of
CH3, is very much closer than would appear from
Nicklès’ results.
Unfortunately, some of the work of Laurent and
Nicklès was not carried out with the care and
accuracy which is indispensable for researches
which are to retain permanent value, and critics
were not slow to arise. Kopp,[5] in 1849, unmercifully
exposed these failings, so that the real kernel
of the work, which was of considerable value, came
into discredit.
Pasteur,[6] however, in 1848, besides the important
observations regarding enantiomorphism, to be
described in Chapter XI., had noticed similar
zonal likenesses between related tartrates, amounting
only therefore to isogonism and not to isomorphism;
for here again the system often differed,
particularly when the members of a series compared
101differed in their water of crystallisation. Thus
there was ample evidence of a really significant
series of facts in the work of these authors, but they
were not properly arranged and explained.
So high was the feeling against the whole subject
carried, however, after Kopp’s memoir, that had
it not been for the steadying influence of Rammelsberg
and Marignac, who themselves carried out
many crystallographic measurements as new substances
continued to be discovered with great
rapidity, the science would have suffered a serious
set-back. Moreover, even Rammelsberg was led
astray in the direction of the views of the chemists
of the time, that isomorphism could be extended
over the crystal system. Frankenheim, whose
discovery of the space-lattice, to be referred to in
the next chapter, will ever render his name famous,
strongly opposed this view. Delafosse, on the
other hand, recognised some truth in both views,
and assumed that there were two kinds of isomorphism,
that of Mitscherlich on the one hand,
and the broader one of Laurent on the other hand,
and that in the case of the latter kind the overstepping
of the system is no bar.
Hjortdahl,[7] in the year 1865, supported the views
of Delafosse more or less, at any rate so far as to
assume the possibility of the existence of partial
isomorphism, that is, of isogonism. He was very
definite, however, against accepting the proposition
that any general law could be applied. He himself
discovered a partial similarity of angles in several
homologous series of organic compounds.
102About this time Sella[8] uttered a warning which
is one worthy of being prominently posted in every
research laboratory, namely, that It is unwise to
make hasty generalisations from the results of a
small number of observations. Were this principle
more generally followed, much greater progress
would in the end be achieved, and without the
discouragement and discredit which inevitably
follows the detection of errors due to lack of broad
experimental foundation. It is certainly an incontrovertible
fact that only such generalisations
as find themselves in accordance with all new but
well-verified experimental facts as they are revealed
can stand the test of time and become accepted
universally as true laws of nature. And it is unreasonable
to expect any generalisation to be of
such a character unless it is already based on so
large a number of facts that there is little fear of
other new ones upsetting them.
Some order was, however, introduced into this
chaotic state of chemical crystallography in the
year 1870 by P. von Groth.[9] He investigated
systematically the derivatives of the hydrocarbon
benzene, C6H6, many of which are excellently
crystallising solids suitable for goniometrical
measurement. He showed that although the crystal
system may be and often is altered, yet there is a
striking similarity in the angles between the faces of
certain zones, which for the purposes of comparison
he arranged to be parallel to each other in his
descriptions of the crystals, so that the relationship
103would then consist in an elongation or a shortening
of this particular zone axis, which was usually a
crystallographic axis. He recognised that this was
a totally different phenomenon from isomorphism,
and called it “morphotropy.” Although it may
possibly be permissible from one point of view to
regard isomorphism as a particular case of complete
morphotropy along all zones, such a course is not
advisable, as morphotropic similarities are frequently
of a comparatively loose and often indeed of a somewhat
vague character, while isomorphous relationships
are governed by very precise laws.
Thus von Groth showed first that benzene,
C6H6, crystallises in the rhombic system with axial
ratios a : b : c = 0.891 : 1 : 0.977. Next, that when
one or two of the hydrogen atoms are replaced
by hydroxyl OH groups the substances produced,
phenol C6H5.OH and resorcinol C6H4(OH)2, are
found also to crystallise in the rhombic system,
and in the second case, for which alone the axial
ratios could be determined, the ratio a : b proved
to be very similar, but the ratio c : b was
different, the actual values being a : b : c = 0.910 :
1 : 0.540. Pyrocatechol, the isomer of resorcinol,
also crystallises in the rhombic system, but the
crystals have not been obtained sufficiently well
formed to enable any deductions to be made from
any measurements carried out with them.
Similarly, the nitro-derivatives of phenol, orthonitrophenol
C6H4.OH.NO2, dinitrophenol C6H3.OH.(NO2)2,
and trinitrophenol C6H2.OH.(NO2)3, also
crystallise in the rhombic system, and with the
following respective axial ratios: 0.873 : 1 : 0.60;
10410.933 : 1 : 0.753; 0.937 : 1 : 0.974. Again, the value for
the ratio a : b is not very different from that of benzene
itself, while the ratio c : b differs considerably in
the first two cases. Similar relations were also found
to hold good in the cases of meta-dinitrobenzene,
C6H4(NO2)2, axial ratios 0.943 : 1 : 0.538, and trinitrobenzene,
C6H3(NO2)3, which possesses the axial
ratios 0.954 : 1 : 0.733.
The introduction of a chlorine or bromine atom
or a CH3 group in place of hydrogen was found by
von Groth to produce more than the above effect,
the symmetry being often lowered to monoclinic,
a fact which had also been observed to occur
in the cases of certain isomers of the substances
quoted above, ortho-dinitrobenzene for instance.
But it was nevertheless observed that the angles
between the faces in the prism zone remained very
similar, the angles between the faces of the primary
prism (110) and (1̄10), for instance, only varying
in eight such derivatives of all three types, whether
rhombic or monoclinic, from 93° 45′ to 98° 51′.
The crystallographic relationships of organic
substances, however, are very much complicated
by the possibilities of isomerism, the ortho, meta,
and para compounds—corresponding to the replacement
of the two hydrogen atoms attached to two
adjacent, alternate, or opposite carbon atoms respectively,
of the six forming the benzene ring—generally
differing extensively and sometimes completely
in crystalline form. Consequently, the phenomenon
of morphotropy is best considered quite
independently of isomorphism.
An interesting intermediate case between morphotropy
105and true isomorphism was investigated by
the author in the year 1890, namely, a series of
homologous organic compounds differing by regular
increments of the organic radicle CH3. They
were prepared by Prof. Japp and Dr Klingemann,
and consisted of the methyl, CH3, ethyl, C2H5,
and propyl, C3H7, derivatives of the substance
triphenyl pyrrholone, all of them being solids
crystallising well. The problem was somewhat
complicated by the development of polymorphism,
the methyl, ethyl, and propyl compounds having
each been found to be dimorphous, and not improbably
trimorphous, but only two varieties of each
salt were obtained in crystals adequately perfect
for measurement. That the production of these
different forms was due to polymorphism and not
to chemical isomerism (different arrangement of the
chemical atoms in the molecule) was shown by the
fact that one variety could be obtained from the other
by simply altering the conditions of crystallisation
from the same solvent. Their identical chemical
composition was established by direct analysis.
The methyl (CH3) compound crystallised in
rhombohedra and in triclinic prisms. The ethyl
(C2H5) derivative was deposited in triclinic prisms
exactly resembling those of the methyl compound
in habit and disposition of faces. A crystal of the
triclinic methyl derivative which would represent
equally well the ethyl compound is shown in Fig.
56. The angles also of the crystals of the two substances
are so similar that one might infer the existence
of true and complete isomorphism. The actual
angular differences rarely exceeded three degrees.
106

Fig. 56.—Crystal of Methyl Triphenyl Pyrrholone.
Besides the triclinic form the ethyl derivative
was also obtained in monoclinic crystals, one of
which is represented in Fig. 57. This illustration
might serve equally well, however, for a
corresponding monoclinic form of the
propyl (C3H7) derivative, and the angles
of these two monoclinic ethyl and propyl
compounds are even closer than those of
the triclinic methyl and ethyl derivatives,
the closeness increasing with the advent
of symmetry.
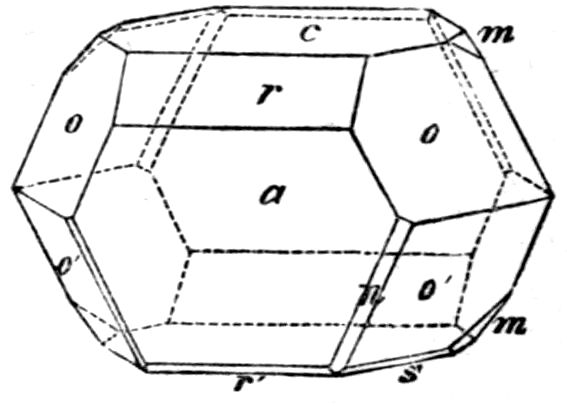
Fig. 57.—Crystal of Ethyl Triphenyl Pyrrholone.
This similarity of angles in the cases
of the two pairs of triclinic and monoclinic
compounds is not only true about
particular zones, but about all the zones,
so that it is a case isomorphism rather
than of isogonism (morphotropy). The
similarity of optical properties is also very close, and
so much so in the cases of the monoclinic crystals
of ethyl and propyl triphenyl pyrrholone that both
exhibit very high dispersion of the optic axes. In the
case of the propyl derivative the difference between
the apparent angle of the
optic axes for red lithium
light and for green thallium
light amounts to 11°. In the
case of the ethyl compound
this difference is enhanced so
considerably that the crystals
afford a remarkable instance
of dispersion of the optic axes
in crossed axial planes, resembling the case of gypsum
discovered by Mitscherlich and described in the
107last chapter, except that the sensitiveness is to
change of wave-length in the illuminating light
rather than to change of temperature. The optic
axial plane is perpendicular to the symmetry plane
for lithium and sodium light, as it is also in the case
of the propyl compound; but in the ethyl derivative
it crosses over for thallium light and rays beyond
that towards the violet, into a plane at right angles to
the former plane, namely, the symmetry plane itself.
The total dispersion between the two axes as separated
in the one plane for red light, and as separated in
the other perpendicular plane for blue light, is more
than 70°. Fig. 58, Plate XIII., shows the nature of
the interference figures afforded in convergent polarised
light of different wave-lengths by a section-plate
perpendicular to the first median line. The figure
at f represents what is observed in white light, as far
as is possible by a drawing in black and white. It
consists of a series of concave coloured curves, falling
in between the arms of the cross, and looping round
the axes, a figure very much like that afforded by
brookite and triple tartrate of ammonium, potassium,
and sodium, the substances already mentioned
in Chapter VII. as being similarly very sensitive
to change of wave-length. The figure in red monochromatic
lithium light is shown at a in Fig. 58,
and that for yellow sodium light at b, the axes being
now much closer together. On changing to green
thallium light the line joining the optic axes becomes
vertical instead of horizontal, as shown at d.
When, instead of employing monochromatic flames,
the spectroscopic monochromatic illuminator (Fig. 75,
page 193), described by the author some years ago to
108the Royal Society, is employed to illuminate the polariscope,
the source of light being the electric arc, the
change of the figure from that given by the extreme
red of the spectrum to that afforded by the violet
may be beautifully followed, and the exact wave-length
in the greenish yellow determined for which
the crossing occurs and an apparently uniaxial figure
of circular rings and rectangular cross is produced.
For it is possible with the aid of this illuminator
directly to observe the production of the uniaxial
figure. The wave-length is either directly afforded by
the graduation of the fine-adjustment micrometric
drum or is obtained from a curve of wave-lengths,
constructed to correspond to the circle readings of
the illuminator. The appearance of the interference
figure for this critical wave-length is shown at c
in Fig. 58. The remaining figure at e represents
the appearance when a mixture of sodium and
thallium light is employed, which clearly indicates
the four extreme axial positions, and assists in elucidating
the nature of the figure f exhibited in white light.
The second form of the propyl derivative belongs
to the rhombic system, and a similar rhombic form
of the ethyl compound was once obtained, but
lost again on attempting to recrystallise.
These interesting relationships of the homologous
methyl, ethyl, and propyl derivatives of triphenyl
pyrrholone thus appear to form a connecting link
between cases of isogonism or morphotropy and
of true isomorphism.
PLATE XIII.
Fig. 58.—Interference Figures in Convergent Polarised Light of different Wave-lengths afforded by the Monoclinic Variety of Ethyl Triphenyl Pyrrholone; a, in Red Lithium Light; b, in Yellow Sodium Light; c, in Greenish-Yellow Light of the Critical Wave-length for Production of the Uniaxial Figure; d, in Green Thallium Light; e, in mixed Sodium and Thallium Light; and f, in White Light.
(Reproductions of Drawings by the author.)
109We are now, therefore, in a position to approach
the question of true isomorphism, and as leading up
to the fuller treatment of the subject in Chapter X.
we may conclude this chapter by referring first to
one important investigation in which the necessity
for extreme accuracy of measurement and perfection
of material was fully appreciated. This was an
admirable research carried out in the years 1887
and 1888 by H. A. Miers[10] on the red silver minerals,
proustite, sulpharsenite of silver, Ag3AsS3, and
pyrargyrite, the analogous sulphantimonite of silver,
Ag3SbS3, which afforded a further indication of
the existence of real small differences of angle
between the members of truly isomorphous series.
These two minerals form exceptionally beautiful
crystals belonging to the trigonal system, the
hexagonal prism being always a prominent form,
terminated by the primary and other rhombohedra,
scalenohedra and various pyramidal forms, many of
the crystals being exceedingly rich in faces. When
the crystals are freshly obtained from the dark
recesses of the silver mine they are very lustrous
and transparent, but they are gradually affected
by light, like many silver compounds, and require
to be stored in the dark in order to preserve their
transparency. A magnificent crystal of proustite
from Chili is one of the finest objects in the British
Museum at South Kensington, but is rarely seen
on account of the necessity for preservation from
light. Pyrargyrite is generally dark grey in
appearance, and affords a reddish-purple “streak”
(colour of the powder on scratching or pulverising).
Proustite, however, possesses a beautiful scarlet-vermilion
colour, and affords a very bright red streak.
Now these two beautiful minerals are obviously
110analogous compounds of the same metal, silver,
with the sulpho-acid of two elements, arsenic and
antimony, belonging strictly to the same family
group, the nitrogen-phosphorus group, of the
periodic classification of the elements according to
Mendeleéff. Consequently, they should be perfectly
isomorphous. Miers has shown in a most complete
manner that they are so, that they occur in very
perfect crystals of similar habit belonging to the
same class of the trigonal system, the ditrigonal
polar class, both minerals being hemimorphic, that
is, showing different forms at the two terminations,
in accordance with the symmetry of the polar class
of the trigonal system. But the angles of the two
substances were not found to be identical, although
constant for each compound within one minute
of arc, there being slight but very real differences,
which are very well typified by the principal angle
in each case, that of the primary rhombohedron.
In the case of proustite it is 72° 12′, while the rhombohedron
angle of pyrargyrite is 71° 22′.
This interesting and beautiful investigation of
Miers thus gave us an inkling of the truth, that
small angular differences do exist between the
members of isomorphous compounds. It paved
the way for, and indeed partly suggested, the
author’s systematic investigation of the sulphates,
selenates, and double salts of the alkali series of
metals, a brief account of the main results of which
will be given in Chapter X.
111
CHAPTER IX
THE CRYSTAL SPACE-LATTICE AND ITS MOLECULAR UNIT CELL. THE 230 POINT-SYSTEMS OF HOMOGENEOUS CRYSTAL STRUCTURE.
The interval between the morphotropic work described
in the last chapter and the present time has
been remarkable for the completion of the geometrical
and mathematical investigation, and the successful
identification, of all the possible types of homogeneous
structures possessing the essential attributes of
crystals. It has now been definitely established that
there are 230 such types of homogeneous structures
possible, and the whole of them conform to the conditions
of symmetry of one or other of the thirty-two
classes of crystals. This fact is now thoroughly
agreed upon by all the authorities who have made
the subject their special study, and may truly be
considered as fundamental.
There has long been a consensus of opinion that
the crystal edifice is built up of structural units
which can be likened to the bricks or stone blocks
of the builder, but which in the case of the crystal
are so small as to be invisible even under the highest
power of the microscope. The conceptions of their
nature, however, have been almost as numerous as
the investigators themselves, everyone who has
thought over the subject forming his own particular
112ideas concerning them. We have had the “Molécules
intégrantes” of Haüy, the “Polyhédres” of
Bravais, the “Fundamentalbereich” of Schönflies,
the “Parallelohedra” of von Fedorow, and the
fourteen-walled cell, the “Tetrakaidecahedron”
of Lord Kelvin, and again the “Polyhedra” of
Pope and Barlow. Ideas have thus been extremely
fertile, and indeed almost every variety of speculation
has been indulged in as to the shape and nature
of the unit of the structure which can exhibit such
remarkable evidences of organisation and such extraordinary
optical and other physical properties
as those of a crystal.
There is one inherent difficulty, however, which
renders all such speculations more or less chimerical,
until we know very much more as to the structure
of the chemical atom, and the organisation of the
corpuscles composing it. Such speculations, however,
are deeply interesting, and the difficulty alluded to
accounts largely for the great variety of conception
possible. It is this, that the matter of the molecules,
and again that of the atoms composing them, is not
necessarily, nor even probably, continuous and in
contact throughout, but that on the contrary the
space which may legitimately be assigned to the
unit of the structure is partly void. How much of
this unit space is matter and how much is unoccupied,
and how the one is related to the other as regards its
position or distribution in space, we have yet no
means of knowing, although there are signs that the
day is not far distant when we shall know at least
something concerning it. The recent brilliant work
of Sir J. J. Thomson and his school of physicists
113has rendered it clear that the chemical atom is
composed of cycles of electronic corpuscles, the
orbital motions of which determine its boundaries.
In this condition of our knowledge obviously
the only safe course is to consider each atom of
the chemical molecule as occupying a “sphere of influence,”
within the limits of which the material
parts of the atom, the corpuscles in organised motion,
are confined. The “Fundamentalbereich” of Schönflies
and the “Sphere of Influence” of Barlow, are
the conceptions which in all probability have the
greatest value in the present state of our knowledge,
and if we adopt the latter we shall not be committing
ourselves to anything more than the experimental
facts fully warrant.
It may be quite definitely stated, however, that
there is a considerable amount of experimental
evidence that the unit of the space-lattice of the
crystal structure is certainly not more complex
than the chemical molecule, the idea of an aggregation
of chemical molecules to form a “physical molecule”
acting as a structural unit having proved to be a
misleading myth.
Fortunately, however, there is no necessity whatever
to introduce the subject of the actual shape
of the unit, and the greatest progress has been effected
by disregarding it altogether, and agreeing to the
representation of the unit by a point. This
leads us at once to perceive the importance of the
brilliant work of the geometricians, who have now
completed their theory of the homogeneous partitioning
of space into point-systems possible to crystals,
the structural units of the latter being regarded as
114points. The investigations extend from those of
Frankenheim in the year 1830 to the finishing
touches given by Barlow in 1894, and prominently
standing forth as those of the greatest contributors
to the subject, besides the two investigators just
mentioned, are the names of Bravais, Sohncke,
Schönflies and von Fedorow.
Bravais, perfecting the work of his predecessor
Frankenheim, made us acquainted with the fourteen
fundamentally important space-lattices, or same-ways
orientated arrangements of points. If we
regard each chemical molecule as represented by a
point, disregarding the separate atoms of which
it is composed, then these fourteen space-lattices
represent the possible arrangements of the molecules
in the crystal in all the simpler cases; three of
these lattices have cubic symmetry; the tetragonal,
hexagonal, trigonal, rhombic and monoclinic systems
claim two space-lattices each; while one space-lattice
conforms to the lack of symmetry of the triclinic
system.
The fourteen space-lattices of Bravais thus represent
the arrangement of the chemical molecules in
the crystal, and determine the systematic symmetry.
The points being taken absolutely analogously in
all the molecules, and the whole assemblage being
homogeneous, that is, such that the environment
about any one spot is the same as about every other,
the arrangement is obviously a same-ways orientated
one, the molecules being all arranged parallel-wise
to each other.
Fig. 59.—Triclinic Space-Lattice.
But the fact that the structure is that of a space-lattice
also causes the crystal to obey the law of
115rational indices. To enable us to see how this comes
about it is only necessary to regard a space-lattice.
In Fig. 59 is represented the general form of space-lattice,
that which corresponds to triclinic symmetry.
It is obviously built up of parallelepipeda, the edges
of which are proportional to the lengths of the three
triclinic axes, and their mutual inclinations are
those of the latter.
As we may take our
representative point
anywhere in the
molecule, so long as
the position chosen
is the same for all
the molecules of the
assemblage, we may
imagine the points
occupying the
centres of the parallelepipeda
instead
of the corners if we
choose, for that
would only be
equivalent to moving
the whole space-lattice slightly parallel to
itself. Hence, each cell may be regarded as the
habitat of the chemical molecule.
Now the faces of the crystal parallel to each
two of the three sets of parallel lines forming the
space-lattice will be the three pairs of axial-plane
faces, and any fourth face inclined to them must be
got by removing parallelepipedal blocks in step-wise
fashion, precisely like bricks, as already shown in
116Fig. 12 (page 28) in Chapter III., in order to illustrate
the step by step removal of Haüy’s unit blocks. It
will readily be seen that if one more cell be removed
from each row than from the row below it, the line
of contact touching the projecting corner of the last
block of each row will be inclined more steeply than
if two more cells were removed from each row. Moreover,
the angle varies considerably between the two
cases, and if three blocks are removed at a time the
angle gets very small indeed. Hence, there cannot be
many such planes possible, and we see at once why
the indices of the faces developed on a crystal are
composed of low whole numbers and why the forms
are so relatively few in number. Owing to the
minuteness of a chemical molecule, all the irregularities
of such a surface are submicroscopic, and
the general effect to the eye is that of a smooth
plane surface.
The space-lattice arrangement of the molecules
in the crystal structure thus causes the crystal
to follow the law of rational indices, by limiting
and restricting the number of possible facial forms
which can be developed. It also determines which
one of the seven systems of symmetry or styles
of crystal architecture the crystal shall adopt. It
does not determine the details of the architecture,
however, that is, to which of the thirty-two classes
it shall conform, this not being the function of the
molecular arrangement but of the atomic arrangement
that is, of the arrangement of the cluster of
atoms which form the molecule, and this leads us to
the next step in the unravelling of the internal
structure of crystals.
117The credit of this next stage of further progress
is due to Sohncke, whose long labours resulted
in the discrimination and description of sixty-five
“Regular Point-Systems,” homogeneous assemblages
of points symmetrically and identically
arranged about axes of symmetry, which are sometimes
screw axes, that is, axes about which the points
are spirally distributed. Sohncke’s point-systems
express the number of ways in which symmetrical
repetition can occur. Moreover, the points may
always be grouped in sets or clusters, the centres
of gravity of which form a Bravais space-lattice.
This latter fact is of great interest, for it means
that Sohncke’s points may represent the chemical
atoms, and that the stereometric arrangement of
the atoms in the molecule is that which produces
the point-system and determines the crystal class,
while the whole cluster of atoms forming the molecule
furnishes, as above stated, the representative point
of the space-lattice.
This, however, is not the whole story, for the sixty-five
Sohnckian regular point-systems only account
for twenty-one of the thirty-two crystal classes,
the remaining eleven being those of lower than full
holohedral systematic symmetry, and which are
characterised by showing complementary right and
left-handed forms. In other words, they exhibit
two varieties, on one of which faces of low
symmetry are developed on the right, while on
the other symmetrically complementary faces are
developed on the left; that is, these little faces modify
on the right and left respectively the solid angles
formed by those faces of the crystal which are
118common to both the holohedral class of the system
and to the lower symmetry class in question. In
some cases, moreover, these two complementary
forms are known to exist alone, without the presence
of faces common to both the holohedral class and
the class of lower symmetry. The two varieties of
the crystals are the mirror images of each other, being
related as a right-hand glove is to a left-hand one.
Further, the crystals of these eleven classes very
frequently exhibit the power of rotating the plane
of polarised light to the right or to the left, and
complementarily in the cases of the two varieties
of any one substance, corresponding to the complementariness
of the two crystal forms. The
converse is even more absolute, for no optically
active crystal has yet been discovered which does
not belong to one or other of these eleven classes
of lower than holohedral symmetry.
The final step of accounting for the structure of
these highly interesting eleven classes of crystals
was taken simultaneously by a German, Schönflies,
a Russian, von Fedorow, and an Englishman,
Barlow, who quite independently and by totally
different lines of reasoning and of geometrical
illustration showed that they were entirely accounted
for by the introduction of a new element of symmetry,
that of mirror-image repetition, or “enantiomorphous
similarity” as distinguished from “identical
similarity.” These three investigators all united
in finally concluding that when the definition of
symmetrical repetition is thus broadened to include
enantiomorphous similarity, 165 further point-systems
are admitted, and the whole 230 point-systems
119then account for the whole of the thirty-two
classes of crystals.
Schönflies’ simple definition of the nature of the
structure is that every molecule is surrounded by the
rest collectively in like manner, when likeness may
be either identity or mirror-image resemblance. Von
Fedorow finds the extra 165 types to be comprised in
“double systems” consisting of two “analogous
systems” which are the mirror images of each other.
Barlow proceeds to find in how many ways the two
mirror-image forms can be combined together, there
being in general three distinct modes of duplication,
including the insertion of one inside the other. He
also shows that all homologous points in a structure
of the type of one of these additional 165 point-systems
together form one of the 65 Sohnckian
point-systems, the structure being capable of the
same rotations or translations, technically known
as “coincidence movements” (movements which
bring the structure to exhibit the same appearance
as at first), as those which are characteristic of that
point-system.
This fascinating subject of mirror-image symmetry,
and the optical activity connected with it,
will be reverted to and the latter explained in
Chapter XI.
We have thus seen how satisfactorily the geometrical
theory of the homogeneous partitioning of
space has been worked out, and how admirably it
agrees with our preliminary supposition that a
crystal is a homogeneous structure. The fact that
the 230 homogeneous point-systems all fall into and
distribute themselves among the thirty-two classes
120of crystals, the symmetry of which has also now
been fully established, affords undeniable proof
that as regards this branch of the subject something
like finality and clearness of vision has now been
arrived at.
121
CHAPTER X
LAW OF VARIATION OF ANGLES IN ISOMORPHOUS SERIES. RELATIVE DIMENSIONS OF UNIT CELLS. FIXITY OF ATOMS IN CRYSTAL.
We are now in a position to approach the conclusion
of the long controversy as to the constancy or
otherwise of crystal angles in the cases of greatest
similarity, those of isomorphous substances, and to
appreciate how the conflicting views of Haüy and
Mitscherlich and their schools of thought have at
length been reconciled. As the result of a comprehensive
study, on the part of the author, of the
sulphates and selenates of the rhombic series
R2S
SeO4, and of the double sulphates and selenates
of the monoclinic series R2M(S
SeO4)2.6H2O, in which
R represents the alkali metals, potassium, rubidium
and cæsium, and in which M may be magnesium,
zinc, iron, nickel, cobalt, manganese, copper or cadmium,
four facts of prime significance have been
definitely established.
(1) The crystals of the different members of an
isomorphous series exhibit slight but real differences
in their interfacial angles, the magnitude of the angle
changing regularly with the alteration of the atomic
weight of the interchangeable metals or negative
elements of the same family group which give rise to
122the series, as one metal or acid-forming element
is replaced by another. The amount of the difference
increases as the symmetry of the system diminishes.
Thus the maximum difference for the more symmetrical
rhombic series of sulphates and selenates
is 56′, which occurs in the case of one angle between
potassium and cæsium selenates, and it is usually
much less than this; in the case of the less symmetrical
monoclinic series of double salts the maximum
angular difference observed was 2° 21′, between
potassium and cæsium magnesium sulphates.
(2) The physical properties of the crystals, such as
their optical and thermal constants, are also functions
of the atomic weights of the elements of the same
family group which by their interchange produce the
series.
(3) The dimensions of the elementary parallelepipedon
of the space-lattice, or in other words, the
separation of the molecular centres of gravity, the
points or nodes of the space-lattice, along the three
directions of the crystal axes, also vary with the
atomic weight of the interchangeable elements.
(4) Specific chemical replacements are accompanied
by clearly defined changes in the crystal structure
along equally specific directions. Thus, when
the metal, say potassium, in an alkali sulphate or
selenate is replaced by another of the same alkali-family
group, rubidium or cæsium, there is a marked
alteration in the crystal angles and in the dimensions
of the space-lattice, corresponding to elongation of
the vertical axis; and when the acid-forming element
sulphur is replaced by selenium, its family analogue,
a similar very definite change occurs, but the expansion
123in this case takes place in the horizontal plane
of the crystals.
Confirmatory results have also been obtained as
regards the morphological constants, the investigations
not extending to the optical or thermal properties,
by Muthmann for the permanganates, and
by Barker for the perchlorates, of the alkali metals.
Hence, there can be no doubt whatever that, as
regards the various series investigated, which are
such as would be expected to afford the most definite
results owing to the electro-positive nature of metals
being at its maximum strength in the alkali group,
the above rules are definite laws of nature.
Thus it is clear that in the cases of isomorphous substances,
which were the only possible exceptions to the
generalisation that to every chemically distinct solid substance
of other than perfect cubic symmetry there appertains
a specific crystalline form, endowed with its own
particular angles and morphological crystal elements,
which are absolutely constant for the same temperature,
the law does really hold, and isomorphous substances
are no exceptions. The law of progression of the
crystal properties according to the atomic weight of
the interchangeable elements affords indeed at the
same time both an amplification of the generalisation
and a precise explanation of its mode of operation
in these cases.
The discovery of the local effect produced by the
two kinds, positive and negative, of chemical replacement,
has a profound bearing on crystal structure.
For it is thereby rendered certain that the atoms
are fixed in the crystal edifice, and therefore in the
molecule in the solid state. It becomes obvious
124that the atoms—in their stereometric positions in the
molecule, being thus fixed in the solid crystal when
the molecules set themselves rigidly in the regular
organisation of the space-lattice—form the points of
the regular point-system of the crystal structure,
which determines to which of the thirty-two classes
of symmetry the crystal shall belong. Any movement
of the atoms in the crystal, other than that
which accompanies change of temperature, and
possibly change of pressure, is thus improbable;
and this experimental proof of their fixity, afforded
by the fact that definitely orientated changes
accompany the replacement of particular atoms,
also doubtless indicates that the latter are located
in the particular directions along which the changes
of exterior angle and of internal structural dimensions
are observed to occur. Stereo-chemistry, which has
made such enormous advances during the last few
years, thus becomes of even greater importance than
Wislicenus and its other originators ever dreamt of.
Within the atoms in the crystal the constituent
electronic corpuscles may be and probably are in
rapid movement, and such physical effects as have
hitherto been ascribed to movement of the atoms
within the crystal are doubtless due to movement
of the electronic corpuscles within them, the sphere
of influence of the atom itself being fixed in space
in the solid crystal, and being doubtless defined by the
area within which the corpuscular movements occur.
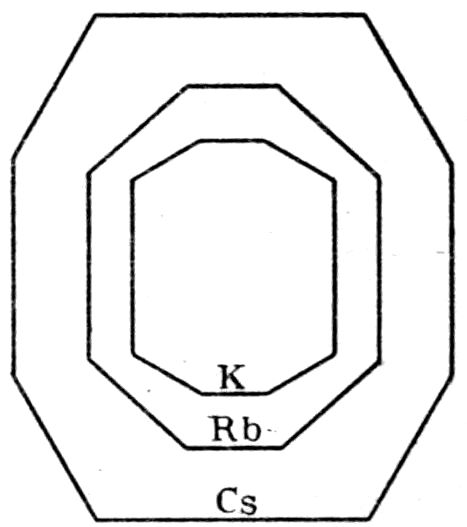
Fig. 60.—Diagram illustrating Progressive Change of Crystal Angles in Isomorphous Series.
Three illustrations of the law of change of the
crystal properties with variation of the atomic
weight of the determinative elements of an isomorphous
series may be given, and will serve to render
125the practical meaning of the generalisation clearer.
The first is a diagrammatic representation, in Fig.
60 (in a very exaggerated manner as the real change
would be inappreciable on the scale drawn), of the
change of angle on replacing the potassium in
potassium sulphate, K2SO4, or selenate, K2SeO4,
by rubidium or cæsium. The inner crystal outline,
a vertical section, is that of the potassium salt.
The vertical lines represent the intersections of the
two faces of the brachypinakoid b = {010} with a
vertical plane parallel to the
macropinakoid a = {100}; the
horizontal lines represent the intersection
of the two faces of the
basal plane c = {001} with the same
vertical plane; and the oblique
lines represent the intersection of
the vertical plane with the four
faces of the dome form q = {011},
which are inclined to both b and
c planes. The diagram is thus
designed to show the variation of
the inclination of these latter dome faces to the two
rectangular axial plane faces b and c. The outer
crystal outline represents a similar section of a
crystal of the corresponding cæsium salt, and the
middle outline that of a crystal of the rubidium salt.
The progressive alteration of the angle of the
q-face will be obvious, the direction of the change
being correct, but the amount of change, as already
stated, being much exaggerated; in reality it never
reaches a degree between the two extreme (potassium
and cæsium) salts. It will be remembered that the
126respective atomic weights of potassium, rubidium, and
cæsium are 38·85, 84·9 and 131·9, when hydrogen equals
1, that of rubidium being almost exactly the mean.
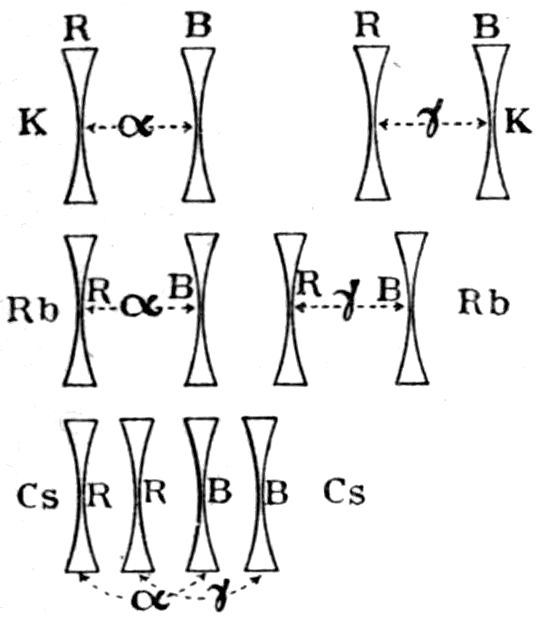
Fig. 61.—Diagram illustrating Progressive Change of Double Retraction in Isomorphous Series.
The second illustration is taken from the optical
properties. Fig. 61 represents graphically the regular
diminution of double refraction (the difference between
the two extreme indices of refraction α and γ) which
accompanies increase of the atomic weight of the
metal present. The diagram exhibits the closing
up of the two spectra afforded by three analogously
orientated 60°-prisms, one of
each of the three salts, such as
was used in determining two of
the refractive indices of the salt.
Each prism produces two refracted
rays from the single
ray furnished by the collimator
of the spectrometer, and consequently
two images of the
signal-slit of the collimator
when monochromatic light is
used, or two spectra if white
light be employed. The
Websky signal-slit is narrow at the centre to enable an
accurate allocation to the vertical cross-wire of the telescope
to be made, but wide at its top and bottom ends,
in order to transmit ample light, and Fig. 61 shows
four images of this signal produced by each prism,
namely, one R in red C-hydrogen light and another B
in greenish-blue F-hydrogen light belonging to each
of the two spectra, in order to locate the two ends
of each of the latter, coloured monochromatic light
of each of the two colours in turn and of the exact
127C and F wave-lengths having been fed to the spectrometer
from the spectroscopic illuminator. It will
be observed in the case of the top row that the two
spectra, each indicated by the adjacent red and
greenish-blue images, are well apart, the relative
distance being about that actually observed in the
case of potassium sulphate. They are nearer together,
however, in the second row, which indicates
what is observed in the case of the analogous rubidium
salt, and in the lowest row representing the relative
distances of the two spectra apart in the case of the
cæsium salt, they are so close together as to overlap;
for in this latter case the greenish-blue image of the
left-hand spectrum, corresponding to the a index of
refraction, occupies the same position as the image
for yellow sodium light of the right-hand spectrum
corresponding to γ would occupy in the case of
cæsium sulphate, the a refractive index for F-light
being 1·5660 and the γ index for Na-light being
1·5662. The progression of the alteration of the
amount of the double refraction is thus very striking,
as the atomic weight of the metal is varied.
The third illustration of the law of progression
with atomic weight is also an optical one, and is
taken from the monoclinic series of double sulphates
and selenates. It indicates the rotation, with increase
of the atomic weight of the metal, of the
ellipsoid which graphically represents the optical
properties, about the unique axis of symmetry, which
is likewise an axis of optical symmetry, of the crystal.
In the potassium salt the ellipsoid occupies the position
indicated by the ellipse drawn in continuous
line in Fig. 62, the section of the ellipsoid by the
128symmetry plane; the outline of a tabular crystal
parallel to the symmetry plane is also given, as well
as the axes of the crystal and of the ellipsoid lying
in that plane.
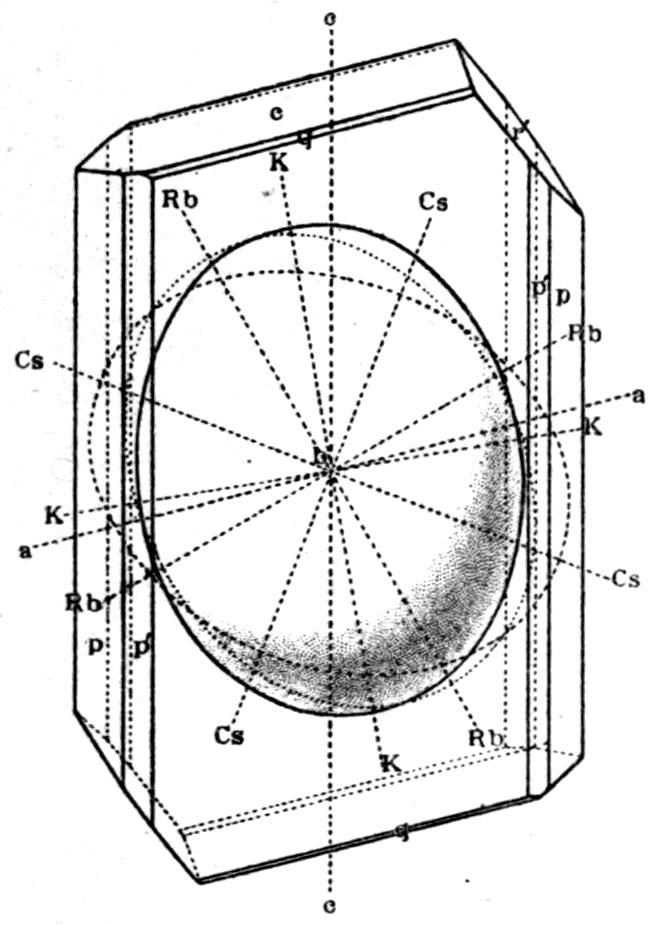
Fig. 62.—Diagram illustrating Progressive Rotation of Optical Ellipsoid in Monoclinic Isomorphous Series.
In the rubidium salt the ellipsoid has rotated
over to the left, as indicated by the dotted ellipse,
for a few degrees, the number of which varies
slightly for the different groups of double salts;
while in the cæsium salt it has swung over much
more still, to the place
marked by the ellipse
drawn in broken line. In
both this and the last
illustration it will be remarked
that the optical
change is greater between
the rubidium and cæsium
salts than it is between the
potassium and rubidium
salts, the reason being that
the optical properties are
usually functions (of the
atomic weight of the interchangeable
elements) which
are of an order higher than
the first corresponding to
simple proportionality.
These three ocular illustrations may serve to
render this interesting law of progression, according
to the atomic weight of the interchangeable elements
which give rise to the isomorphous series, clearer to
the mind, by placing before it concrete instances of
the operation of the law.
129The generalisation itself may be very concisely
expressed in the statement that:
The whole of the properties, morphological and
physical, of the crystals of an isomorphous series of
salts are functions of the atomic weights of the interchangeable
chemical elements of the same family
group which give rise to the series.
The fact that this law extends to the structural
dimensions, equally with all other morphological
properties, as stated under (3) at the beginning of this
chapter, is of especial interest. For it has actually
been found possible to determine the relations of the
dimensions of the unit parallelepipeda of the space-lattices
of the various salts, that is, the separation
of the molecular points of the space-lattice in the
directions of the three crystal axes, for the various
salts of the isomorphous series. This is achieved
by combining in suitable formulæ the volume of
the unit cell of the space-lattice with the relative
lengths of the three crystal axes, a, b, c.
The axial ratios a : b : c are calculated from the
measurements of the crystal angles, as explained in
Chapter VI., page 68, and the volume is the physical
constant long known as “molecular volume,” but now
for the first time understood as regards its meaning
in the case of solid substances. It is the quotient of
the chemical constant molecular weight (the sum
of the atomic weights, taking into account the
number of atoms of each element present) by the
specific gravity of the substance, here the solid
crystal. Very great care has been taken to obtain
absolutely accurate determinations of the specific
gravities of the salts, as much depends on this now
130very valuable physical constant, and all the values
obtained were reduced to the constant reference
temperature of 20°, as the density notoriously alters
rapidly with change of temperature.
We have thus arrived at morphological constants
of very considerable importance, which are best
termed “Molecular Distance Ratios,” as they express
the relative distances apart in the three directions
of space of the centres of gravity or other representative
points of contiguous chemical molecules.
They are dependent on three experimental determinations,
atomic weight, specific gravity, and
crystal angles, all of which have now been brought
to the highest pitch of refinement and accuracy;
hence the molecular distance ratios are particularly
trustworthy constants. If it were only known how
much is matter and how much is space in the molecular
parallelepipedal cell, we should actually have in these
constants a relative measure of the sizes of the
molecules. They do give us, however, the relative
directional dimensions of the molecular unit parallelepipedal
cells of the space-lattices of the various
members of the isomorphous series, just as the
molecular volumes give us the relative volumes of
these cells. For in an isomorphous series we are
absolutely sure that the plan on which the space-lattice
is constructed, its style of architecture, is
identical for all the members of the isomorphous
series. Hence, the molecular distance ratios are
in these cases absolutely valid and strictly comparable.
The ratios are generally expressed by the
Greek letters χ : ψ : ω.
On comparing the molecular distance ratios for a
131potassium, a rubidium, and a cæsium salt of any of
the series of sulphates, selenates, permanganates,
perchlorates, double sulphates or double selenates
investigated, we invariably find that the values of
χ, ψ, and ω for the rubidium salt (rubidium having
the intermediate atomic weight) lie between the
analogous sets of three values for the potassium and
cæsium salts respectively, in complete accordance
with the law.
For the generalisation to apply absolutely it is
essential that the interchangeable elements shall
belong strictly to the same family group of the
periodic classification of Mendeleéff. Potassium,
rubidium, and cæsium fulfil this condition absolutely,
and so the law of progression of the crystal properties
with the atomic weight of the interchangeable
elements applies rigidly to their salts. Now
there are two bases, the metal thallium and the
complex radicle group ammonium NH4, which are
not thus related to the group of three alkali
metals just mentioned, but which are yet capable
of replacing those metals isomorphously in their
crystals without more change of angle or of structural
constants than is provoked by the replacement of
potassium by cæsium; and often indeed the amount
of change has been singularly like the lesser amount
observed when rubidium has been interchanged for
potassium. But although this is so, the directions of
the changes are irregular, being sometimes the same
as when rubidium or cæsium is introduced, and
sometimes contrariwise, and in the case of thallium
there are also striking optical differences, the thallium
salts being exceptionally highly refractive. Still,
132morphologically the ammonium and thallium salts
may legitimately be included in the same isomorphous
series with the salts of potassium, rubidium,
and cæsium, and a somewhat wider interpretation
has to be given to the term “isomorphism” in order
to admit these cases. To distinguish the inner group
formed by family analogues, that is, the more exclusive
group obeying the law of progression according
to the atomic weight, the term “eutropic”
is employed.
Thus the “isomorphous series” of rhombic sulphates,
selenates, permanganates, and perchlorates,
and the monoclinic series of double sulphates and
double selenates, comprise the potassium, rubidium,
cæsium, thallium and ammonium salts and double
salts of sulphuric, selenic, permanganic, and perchloric
acids, while the inner more exclusive “eutropic series,”
following the law absolutely, comprises in each case
only the salts containing the family analogues,
potassium, rubidium, and cæsium.
In this beautiful manner has the controversy between
the schools of Haüy and Mitscherlich now been
settled, the interesting law described in this chapter
having definitely laid down the true nature and
limitations of isomorphism, while at the same time
absolutely proving as a law of nature the constancy
and specific character of the crystal angles of every
definitely chemically constituted substance.
133
CHAPTER XI
THE EXPLANATION OF POLYMORPHISM, AND THE RELATION BETWEEN ENANTIOMORPHISM AND OPTICAL ACTIVITY.
Polymorphism. It has been shown in Chapter VII.
that Mitscherlich had in several instances proved
the possibility of the occurrence of the same substance
in two different forms, notably sodium dihydrogen
phosphate NaH2PO4.H2O, calcium carbonate CaCO3
(as calcite and aragonite), the metallic sulphates
known as vitriols, and the chemical element sulphur,
and that he gave to the phenomenon the name
“dimorphism.” Since that time large numbers
of dimorphous substances have been discovered, and
several which occur in three forms and even a few
in no less than four totally distinct forms. Until
the establishment of the geometrical theory of
crystal structure, as expounded in Chapter IX.,
this phenomenon of polymorphism gave rise to
endless fruitless discussion. It was most generally
attributed to the different nature of the so-called
“physical molecule,” which was supposed to be
an aggregate of chemical molecules and the unit
of the space-lattice determining the crystal system;
the different polymorphous varieties were supposed
to be built up of structural units or physical molecules
consisting of an aggregation of a different
number of chemical molecules. Several attempts
134were made by various investigators, notably by
Muthmann and by Fock, to determine the number
of chemical molecules constituting the physical
molecule.
All these efforts, however, ended unsatisfactorily,
and in the year 1896 the author showed, in a memoir[11]
on “The Nature of the Structural Unit,” that in
general the physical molecule is a myth, and that
the chemical molecule is the only structural unit
possessing the full chemical composition of the
substance in question; and that its centre of
gravity, or better, any representative point within
it, such as a particular atom, is the unit point of the
Bravais space-lattice of the crystal structure, while
the atoms of which the chemical molecule are composed,
arranged stereometrically identically similarly
in all the molecules, are the points of the individual
point-systems which make up the combined point-system.
This does not imply a necessarily parallel
and identically orientated arrangement of all the
molecules, as at first postulated by Sohncke and
which is a fact for his sixty-five point-systems;
for in accordance with the conclusions of Schönflies,
von Fedorow, and Barlow discussed in Chapter IX.,
cases are possible in which alternate molecules may
be arranged as each other’s mirror images. Such
are the cases of external molecular compensation
or molecular combination, two oppositely enantiomorphous
sets of molecules balancing each other
within the structure, but by exterior compensation
as regards the molecule itself. Moreover, the
principle of mirror-image symmetry enters, as stated
135in Chapter IX, altogether into the constitution
of no less than 165 of the 230 types of homogeneous
structure possible to crystals.
Hence the conception of a physical molecule
is totally unnecessary and, moreover, erroneous.
The alkali sulphates and selenates exhibit dimorphism,
one member of the series, ammonium selenate,
having only hitherto been observed in the pure state
in the second, monoclinic, form, and never in the
ordinary rhombic form; and the author has conclusively
proved for these salts, and also for the
double salts which they form with the sulphates
and selenates of magnesium, zinc, iron, nickel,
cobalt, manganese, copper, and cadmium, that the
chemical molecule is the only kind of molecule present,
and that its representative points are, as just stated,
the nodes of the Bravais space-lattice of the crystal
structure, determining both the system of the
crystal and its obedience to the law of rational
indices.
The explanation of polymorphism thus proves,
in the light of the results which have now been laid
before the reader, to be a remarkably simple one.
Special pains were taken in explaining those results
to show that the temperature had a great deal to do
with the conditions of equilibrium of the crystal
structure, for it determines the intermolecular
distances, that is, the amount of separation of the
molecules, and thus controls their possibility of
movement with respect to one another. Now the
behaviour of the chemical molecules on the advent
of crystallisation is undoubtedly largely influenced
by the stereometric arrangement of the atoms
136composing them, and it is possible for the latter to
be such that the molecules may take up several
different parallel or enantiomorphously related positions;
or as we have just seen, a regular alternation
within the crystal structure of such mirror-image
positions may be taken up. These different arrangements,
whether parallel or enantiomorphously
opposite, may be, and probably will be, of different
degrees of stability, each of these different
forms finding its maximum stability of equilibrium
at some particular temperature, which is different
for the different varieties. Hence, at a series of
ascending or descending temperatures, assuming the
pressure to remain the ordinary atmospheric, these
different types of homogeneous crystal structures
will be most liable to be produced, each at its own
particular temperature, for which stable equilibrium
of that crystal structure occurs.
These different assemblages are as a rule quite
dissimilar, certainly in the crystal elements, often
in class and not infrequently in system. Generally
two such different crystalline forms are all that
are possible within the life-range of temperature of
the substance. But occasionally three or even as
many as four such different forms are found to be
capable of existence within the temperature life-limits
of the substance.
Polymorphism is thus completely and simply
explained as a direct result of the establishment
of the geometrical theory of crystal structure as
laid down in Chapter IX. The equilibrium of the
homogeneous structure is a function of the temperature,
and the stereometric arrangement of the atoms
137in the chemical molecule of a substance may be such
as permits of two or more homogeneous arrangements
of the molecules in assemblages of varying degrees
of stability, but each of which has a maximum
stability at a particular temperature. Hence, within
any given range of temperature such a substance
will assume that type of homogeneous arrangement
of its molecules in a crystal which corresponds to the
stablest equilibrium within these temperature limits,
assuming the pressure constant within the bounds of
the usual atmospheric variations. Employing the
language of physical chemistry, such a substance
will thus present two or more different solid
“phases,” each characterised by its specific crystalline
form, the elementary parallelepipedon of which is
quite a distinct one. Each phase possesses also
its own specific optical and other physical properties,
such as melting point, solubility, thermal expansion,
and elasticity.
It would appear as if the element sulphur is also
polymorphous in this sense, for the monoclinic prismatic
form (Fig. 2, Plate I.)—the best known and most
easily prepared, from the state of fusion, of all the
forms other than the common rhombic form, in which
sulphur is found in the neighbourhood of volcanoes
and in which it is also deposited from solution in
carbon bisulphide—is of distinctly lower stability, the
crystals passing in a few days into powder composed
of minute crystals of the stable rhombic variety. But
in the case of carbon, with its totally different and
apparently at ordinary temperatures equally stable
varieties of octahedral-cubic diamond (Fig. 82, Plate
XVI.) and hexagonal graphite, there is some doubt;
138for although the diamond is converted into graphite at
a red heat in the electric arc, it is doubtful whether
we are not in the presence of a case of chemical polymerism
or allotropy, like the case of ozone, where three
atoms of oxygen compose the molecule, instead of the
two atoms in the molecule of ordinary oxygen. The
fact that the negatively electrified electronic
corpuscles of the Crookes tube cause the same conversion
of diamond into graphite, producing according
to Parsons and Swinton a temperature of 4,890° C.
in the act, is evidence in favour of allotropy, as the
charged corpuscles are a very likely agent for
breaking down such atomic combinations. Moreover,
diamond is volatilised out of contact with
air at 3,600° C. without liquefaction, and the vapour
when cold condenses as graphite. But there is reason
to believe, from experiments by Sir Andrew Noble
and Sir William Crookes, that under great pressure
carbon does liquefy at 3,600° C., and that the liquid
drops on cooling crystallise as diamond.
The yellow and red varieties of phosphorus may
also be due to a similar cause, the yellow variety,
which forms excellent crystals, corresponding to P4,
while the red variety may correspond to a molecule
composed of a different number of atoms than four.
Another view of the nature of polymorphism has
lately been brought forward by Lehmann, as the
result of his remarkable experimental discovery of
“liquid crystals,” to which fuller reference will be
made in Chapter XVI. This new view is, however,
but an amplification of the foregoing explanation
of polymorphism, indicating the possible mode in
which the stereometric position of the atoms in the
139molecule does actually influence and even determine
the particular homogeneous structure which shall be
erected, and explains why the temperature plays
such an important rôle. Lehmann’s theory is that
any one definitely stereometrically constituted
chemical molecule can only display one particular
homogeneous structure and form of crystal, and that
when at a particular temperature the system or class
of symmetry is altered, this occurs because the
stereometric arrangement of the atoms within the
molecule is altered, that is, a new form of molecule
is produced, which naturally gives rise to a new form
of crystal. As far as the author understands it,
this does not mean an isomeric change from the
chemical point of view, the chemical compound
remaining the same, but that the stereometric positions
of the atoms have been changed, without
altering their chemical attachments, but sufficiently
to change the nature of the point-system which they
produce. A significant fact in support of this view
is that the molecules of the substances forming liquid
crystals are usually very complicated and extended
ones, comprising a large number of atoms, the molecules,
in fact, corresponding in length with the long
names of the organic substances of which they are
generally composed.
Lehmann’s work has certainly proved that the
molecule is endowed with more individuality than
has hitherto been ascribed to it, and he even shows
that there is some ground for believing that his liquid
crystals are such because this directive orientative
force resident in the molecules themselves maintains
them in their mutually crystallographically orientated
140positions even in the liquid state, which may be
and sometimes is as mobile as water. It thus appears
that any general acceptance of Lehmann’s ideas will
only tend to amplify and further explain the nature
of polymorphism on the lines here laid down, the
temperature of conversion of one form into another
being merely that at which either a different homogeneous
packing is possible, or that at which the
stereometric relations of the atoms in the molecule
are so altered as to produce a new form of point-system
without forming a new chemical compound.
Enantiomorphism of Crystalline Form and Optical
Activity. It has already been stated that two
supplementary forms which are similar but not
identical, the one being the inverse or mirror-image
reflection of the other, as a right-hand glove is to
a left-hand one, are termed “enantiomorphous.”
Also it has been shown that all those crystal forms
which have no plane of symmetry, either of simple
symmetry or alternating symmetry (which is equivalent
to saying that no centre of symmetry is present
in addition to no plane of symmetry), are enantiomorphous,
and that such forms belong to eleven
specific classes. It has further been shown that the
introduction of this principle of mirror-image
symmetry or enantiomorphism into the conditions
already laid down by Bravais and Sohncke for a
homogeneous structure, by von Fedorow, Schönflies,
and Barlow, enabled those investigators to derive
the remaining 165 of the 230 possible types of homogeneous
structures compatible with crystal structure,
over and above the 65 already established
by Bravais and Sohncke, and thus to complete the
141geometry of crystal structure, when the units of such
structure are represented by points. Sohncke subsequently
accepted the new principle, and modified
his own theory so as to bring it into line with it.
He exhibited some disinclination, however, at first,
to accept the idea—which is a part of the assumption
of the other three authors just referred to, and which
appears to be absolutely necessary to explain one
or two of the most complicated of the crystal classes—of
the possibility of two enantiomorphous kinds
of molecule being present in the crystal of the same
single substance, the balancing of the two sets
having the effect of producing mirror-image symmetry
of the whole crystal, that is, the development of a
plane of symmetry.
Now the whole subject is of deep interest, both
physical and chemical as well as crystallographical,
inasmuch as it is precisely such substances as show
enantiomorphism,—and can thus exist in two forms,
one of which is the mirror-image of the other and not
its identical counterpart, the two being like a pair
of gloves,—which are found to possess the property
of rotating the plane of polarised light and which
are therefore said to be “optically active.” Moreover,
the property may be displayed by both the
crystals and their respective solutions, or by the
crystals only. If, therefore, two optical antipodes
of the same substance are known, one rotating the
plane of polarisation to the right and the other
rotating it to the same extent to the left, their
crystals invariably exhibit mirror-image symmetry
with respect to each other. The converse does not
necessarily hold good, however, that a crystal possessing
142the symmetry of one of these eleven classes
will always exhibit optical activity.
Pasteur[12] was the first to recognise this important
relation between enantiomorphous crystalline form
and optical activity, in the case of tartaric acid,
which has the empirical formula C4H6O6 and the
constitution:
COOH
|
CHOH
|
CHOH
|
COOH
Tartaric acid was isolated by Scheele in 1769,
and its discovery was described in the very first
memoir of that distinguished chemist. Another
very similar acid, as regards some of its more apparent
properties, was afterwards, in 1819, described by
John of Berlin, and investigated by Gay-Lussac
in 1826; the latter obtained it from the grape juice
deposits of the wine manufactory of Kestner at Thann
in the Vosges. It was still more fully investigated
by Gmelin in 1829, who called it racemic acid (Traubensäure).
But it needed the genius of Berzelius to
prove that it really had the same composition as
tartaric acid, although so different to that acid in
some of its properties.
We have here as a matter of fact, the first instance
brought to light involving the principle of
isomerism, the existence of two or more distinct
143compounds having the same chemical composition as
regards the numbers of atoms of the same elements
present, but differing in chemical or physical properties,
or both, owing to the different arrangement of
those atoms within the molecule. The “isomers” may
be chemical or purely physical; the latter involves no
alteration of the linking of the atoms, but merely of
their disposition in space, and is the kind met with
in the case of the tartaric acids.
Biot, so noted for his optical researches, showed
afterwards that tartaric and racemic acids behave
optically differently in solution, an aqueous solution
of the former rotating the plane of polarisation to
the right whilst that of racemic acid is optically
inactive, not rotating the plane of polarisation at all.
That is, if the dark field be produced in the polariscope,
by crossing the polarising and analysing Nicol
prisms at right angles, tartaric acid solution will
restore the light again, and the analyser will have to
be rotated to the right in order to reproduce darkness.
In the case of tartaric acid, the crystals themselves
also rotate the plane of polarisation, the amount being
as much as 11°.4 in sodium fight for a plate of the
crystal one millimetre thick. On the other hand,
neither the solution nor the crystals of racemic
acid rotate the plane of polarisation at all.
Pasteur’s discovery, made in the year 1848,
consisted in finding that racemic acid is really a
molecular compound of two physical “isomers,”
namely, of ordinary tartaric acid, which, as we
have seen, rotates the plane of polarisation to
the right, and of another variety of tartaric acid
which rotates the beam of polarised fight to the same
144extent to the left. The latter and ordinary tartaric
acid he therefore distinguished as lævo tartaric
acid and dextro-tartaric acid respectively. Pasteur
went even further than this, in discovering yet a
fourth variety of tartaric acid, which is optically inactive
like racemic acid, but which cannot be split
up into two optically active antipodes.
Indeed, it has since been shown that there are
three varieties of this truly inactive tartaric acid;
they are cases of isomerism of the chemical molecule
itself, that is, the stereometric arrangement of the
atoms in the molecule is different in the three cases.
For the molecule of tartaric acid—in common with
the molecules of all carbon compounds the solutions
of which, or which themselves in the liquid state,
rotate the plane of polarisation—possesses an asymmetric
carbon atom, an atom of carbon which is
linked by its four valency attachments to four
different kinds of atoms or radicle groups; indeed,
the molecule of tartaric acid contains two such asymmetric
carbon atoms, namely, the two in the pair of
CHOH groups. For each of these carbon atoms is
linked by one attachment to the carbon atom of the
outer COOH group, by another to an atom of hydrogen,
by a third to the oxygen of the group OH, and by
its fourth attachment to the carbon atom of the other
group CHOH, which carries the rest of the molecule,
that is, this attachment is to the other half-molecule
CHOH.COOH. Hence, it is quite obvious that
there can be two different dispositions of the atoms
in space, one of which would be the mirror-image
of the other, while leaving the arrangement of
the atoms about the two asymmetric carbon
145atoms dissimilar and not symmetrical in mirror-image
fashion. That is, the two dispositions would
render the molecules in the two cases enantiomorphous
with respect to each other, and these two would be
the arrangements respectively in the two optically
active varieties. That this is the correct explanation
of the ordinary dextro variety and the lævo variety
of tartaric acid can now admit of no doubt.
But if the groups round the two asymmetric
carbon atoms are symmetrical in mirror-image
fashion, there will be compensation within the
molecule itself, and the substance will be optically
inactive from internal reasons. This is the explanation
of the optically inactive variety which is
unresolvable into any components. The different
varieties of this inactive form are doubtless due to
the different possibilities of arrangement of the
atoms in each half, while leaving the two halves
round each asymmetric carbon atom symmetrical
to each other.
We now know that the decomposable inactive
variety, racemic acid, may be readily obtained by·
dissolving equal weights of the ordinary dextro
and lævo varieties in water and crystallising the
solution by slow evaporation at the ordinary temperature.
For further investigation has fully borne out
the conclusion of Pasteur, that racemic acid simply
consists of a molecular compound of the two active
varieties. It is thus itself inactive because it is
externally compensated, the two kinds of enantiomorphous
molecules being alternately regularly distributed
throughout the whole crystal structure, the
very case which von Fedorow, Schönflies, and Barlow
146assumed to be possible, and which Sohncke only
tardily admitted. The crystalline form of racemic
acid is, as was to be expected, quite different from
the monoclinic form of the active tartaric acids,
being triclinic; and indeed it is not crystallographically
comparable with the active form, inasmuch
as the crystals of racemic acid contain a
molecule of water of crystallisation, whereas the
active varieties crystallise anhydrous.
Ordinary dextro and lævo tartaric acids crystallise
in identical forms of the sphenoidal or monoclinic-hemimorphic
class of the monoclinic system, the
class which is only symmetrical about a digonal
axis, the unique symmetry plane of the monoclinic
system, which also operates when full monoclinic
symmetry is developed, being absent in this class.
Hence the interfacial crystal angles, the monoclinic
axial angle, and the axial ratios are identical for
the two varieties. But the crystals are hemimorphic,
owing to the absence of the symmetry
plane, and complementarily so, the dextro variety
being distinguished by the presence of only the
right clino-prism {011}, while the lævo variety is
characterised by the presence only of the left-clino-prism
{0̄11}, these two complementary forms,
each composed of only two faces and which on a
holohedral crystal exhibiting the full symmetry
of the monoclinic system would both be present
as a single form of four faces, being never both
developed on the same optically active crystal.
This hemimorphism of the two kinds of crystals
will be rendered clear by Figs. 63 and 64, representing
typical crystals of dextro and lævo tartaric
147acids which are obviously the mirror images of each
other.
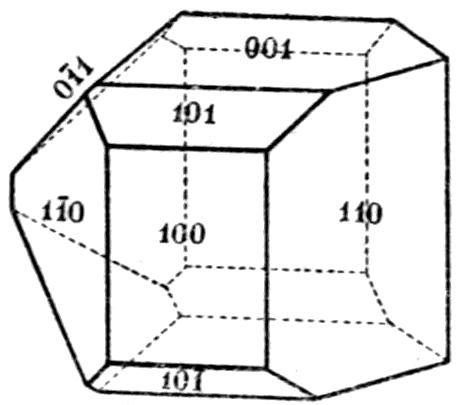
Fig. 64.
Crystals of Dextro and Lævo Tartaric Acids.
A remarkable discovery was made by Pasteur in
connection with one of the salts of racemic acid,
sodium ammonium racemate, Na(NH4)C4H4O6, or
COONH4
|
CHOH
|
CHOH
|
COONa
which is obtained by adding ammonia to the readily
procurable salt hydrogen sodium racemate. Sodium
ammonium racemate was found by Pasteur to
be decomposable into the salts of dextro and lævo
tartaric acids, on crystallisation of a solution
saturated at 28° C. by inoculation with a crystal
of either of those active salts. The solution on
cooling being in the state of slight supersaturation,
which we now know from the work of Ostwald
and of Miers as the metastable condition, corresponding
to the interval between the solubility and supersolubility
curves (see Fig. 98), if a crystal say of sodium
ammonium lævo-tartrate be introduced, this variety
148crystallises out first and can be separated from
the residual dextro-salt, which can then be subsequently
crystallised. Moreover, in certain direct
crystallisations of sodium ammonium racemate
without such specialised inoculation, Pasteur found
all the crystals hemimorphic, some right-handed
and some left-handed, and he was actually able to
isolate from each other crystals of the two varieties.
On separate recrystallisation of these two sets of
crystals, he found them to retain permanently their
right or left-handed character, indicating that the
molecules themselves composing these crystals were
enantiomorphous. Their solutions correspondingly
rotated the plane of polarisation of light in opposite
directions. Pasteur afterwards obtained from the
dextro-salt pure ordinary (dextro) tartaric acid, and
from the lævo-salt the lævo-acid, by converting them
first into the lead salts and then precipitating the
lead as sulphide by sulphuretted hydrogen.
In the case of lævo tartaric acid, this was its first
isolation, as it had hitherto been unknown. Gernez
afterwards independently found that a saturated
solution of sodium ammonium racemate affords
crystals of the lævo-salt just as readily as of the
dextro-salt; if a crystal of either salt be introduced,
crystals corresponding to that variety are produced.
Another most fruitful observation of Pasteur,
the principle of which has since been the means of
isolating one of the two constituents of many racemic
compounds, was that when the spores of Penicillium
glaucum are added to a solution of racemic acid
containing traces of phosphates the ordinary dextro
component is destroyed by the organism, while the
149lævo component is unattacked so long as any dextro
remains; hence, if the fermentation operation be
stopped in time the lævo-acid may be isolated
and crystallised. Why a living organism thus eats
up by preference one variety only, possessing a
particular right or left-handed screw structure, of
a compound containing the same elementary constituents
chemically united in the same manner,
remains a most interesting biological mystery.
The crystals of both dextro and lævo tartaric acids
prove to be pyro-electric, that is, develop electric
excitation when slightly heated. The end which exhibits
the development of the clinodome develops positive
electricity in each case, when the crystal is allowed
to cool after warming, so that the two varieties are
oppositely pyro-electric, just as they are oppositely
optically active. The most convenient method of
demonstrating the fact is to dust a little of Kundt’s
powder, a mixture of finely powdered red lead and
sulphur, through a fine muslin sieve on to the
crystal as it cools. The sulphur becomes negatively
electrified and the red lead positively by mutual
friction of the particles in the sifting, and the sulphur
thus attaches itself to the positively electrified
part of the crystal and the red lead to the negatively
electrified end. This phenomenon of the development
by the two varieties of an optically active
substance of opposite electrical polarity has since
been shown to be a general one.
Finally, on mixing concentrated solutions containing
equivalent weights of dextro and lævo
tartaric acid Pasteur observed that heat was
evolved, a sign of chemical combination, and the
150solution afterwards deposited on cooling crystals of
racemic acid. Hence, the only conclusion possible is
that racemic acid must be a molecular compound of
the two oppositely optically active tartaric acids. It
thus partakes of the character of a double salt,
analogous to potassium magnesium sulphate for
instance. Consequently the crystal structure is
one in which alternating molecules of the two acids
are uniformly distributed, and the case is actually
presented of two oppositely enantiomorphous sets
of molecules producing a homogeneous structure.
This interesting pioneer case of tartaric acid has
been the cause of the term “racemic” being applied
to the inactive form of a substance when it is decomposable
into two oppositely optically active
enantiomorphous varieties of the substance. No
well authenticated exception has been found, in all
the many instances which have been observed of
the phenomenon since Pasteur’s time, to the fact
that optically active substances exhibit what was
formerly termed hemihedrism; that is, expressing
the case in accordance with our later more
accurate ideas of crystal structure as elucidated
in previous chapters, such substances invariably
belong to classes of symmetry possessing less than
the full number of elements of symmetry possible to
the system to which the class belongs. These
classes are eleven in number, those possessing no
plane of symmetry; they are, namely, the asymmetric
class of the triclinic system, the sphenoidal class of
the monoclinic system (to which the two tartaric
acids, dextro and lævo, belong), the bisphenoidal
class of the rhombic system, the pyramidal and
151trapezohedral classes of the trigonal, tetragonal,
and hexagonal systems, and the tetrahedral-pentagonal-dodecahedral
and pentagonal-icositetrahedral
classes of the cubic system.
The optical activity has been proved by Le Bel
and Van t’Hoff to be due in most cases to enantiomorphism
of the chemical molecules, that is, to the
enantiomorphous stereometric arrangement of the
atoms in the molecules, and therefore also,—as we
have just seen, in accordance with the geometrical
theory of crystal structure,—of the combined point-system
in the case of each of the two varieties.
The point-systems are probably of a spiral screw-like
character, either right-handed or left-handed,
as has been shown by Sohncke to be the case for the
two varieties of quartz, which crystallises in the
trapezohedral class of the trigonal system, one of the
eleven classes just enumerated. The example afforded
by quartz will be developed fully in the next two
chapters, as this beautifully crystallised mineral
enables us to study and to demonstrate the phenomena
of optical activity in a unique manner and on
the large scale.
The solutions as well as the crystals are usually
optically active in the cases where, as in the instance
of the tartaric acids, the substances are soluble in
water or other solvent. Occasionally, however, the
optical activity is lost by dissolving in a solvent,
and in such cases it is the point-system only, and not
the molecules themselves, which is enantiomorphous.
Sodium chlorate, NaClO3, is an instance of this kind.
Moreover, a crystal can belong, as already mentioned,
to one of the eleven above enumerated classes of
152symmetry without displaying optical activity, as all
the point-systems possessing the symmetry of these
eleven classes do not exhibit screw-coincidence
movements. Barium nitrate, Ba(NO3)2, is such a
case.
The two “optical antipodes,” as the dextro and lævo
varieties are conveniently termed, of an optically
active substance thus possess an enantiomorphous
crystal structure; but they are alike in their physical
properties such as density, melting point, optical
refraction and optic axial angle, cleavage, and
elasticity. The crystal angles are identical for the
forms which are developed in common by them,
and which are usually those which the particular low
class of symmetry possesses in common with the
holohedral class of the system. The crystallographic
difference between the two varieties comes
in with respect to the specific forms characteristic
of the particular class of lower than full systematic
symmetry, and these forms are never displayed in
common by the two varieties, this being the essence
of the enantiomorphism. When the crystals are
not rich in faces, however, it frequently happens that
only the common forms of higher symmetry just
referred to are developed on the crystals, and the
two varieties are then indistinguishable in exterior
configuration; it is only on testing their rotatory
power, either by means of a section-plate of the
crystal or by means of a solution, or their pyro-electric
properties, or, lastly, their etch-figures
afforded by a trace of a solvent (which etchings
on the crystal faces are enantiomorphous and
an excellent indication of the true symmetry),
153that their real character can be ascertained. Many
mistakes have been made in the past, and crystals
assigned to a higher than their true class of symmetry,
owing to the investigation of only a single crop of
crystals fortuitously poor in the number of forms
displayed.
In the racemic form, if one should be deposited
from the mixed solutions of the two optical antipodes
as a molecular compound of the latter, we have an
occurrence akin to polymerism, that is, the combination
into a single whole entity of a number of
molecules, essentially two in the case of racemism.
Just as polymeric varieties of organic substances are
always found to have quite different crystalline
forms, so an optically inactive racemic form of a
substance is generally quite different crystallographically
to the dextro and lævo varieties. But there
is usually some similarity along specific zones of the
crystals, a kind of isogonism or morphotropy being
developed, such as has been shown to occur, for
instance, by Armstrong and Pope in the case of the
substance sobrerol.[13]
Besides the true racemic form it is often observed
that under certain conditions crystals are obtained
which appear to combine the characters of both the
dextro and lævo varieties, exhibiting both series of distinguishing
hemimorphic or hemihedral forms on the
same crystal; that is, they show the full, holohedral,
symmetry of the system. This has been shown by
Kipping and Pope[14] to be due to repeated twinning,
thin layers of the right and left-handed varieties
being alternated, just, in fact, as in the interesting
154form of quartz known as amethyst, to which reference
with experimental demonstration will be made
in Chapter XIV.; the whole structure assumes in
consequence the simulated higher symmetry which
usually accompanies laminated twinning. Such
forms have been termed “pseudo-racemic.” In their
memoir (loc. cit., p. 993) Kipping and Pope summarise
a large amount of highly interesting work on this
chemico-crystallographic subject which has been
carried out by them, and it may be useful to quote
their precise definition of the relationship between
racemic and pseudo-racemic substances. They say:
“We define a pseudo-racemic substance as an
intercalation of an equal, or approximately equal,
proportion of two enantiomorphously related components,
each of which preserves its characteristic
type of crystalline structure, but is so intercalated
with the other as to form a crystalline individual
of non-homogeneous structure. A solid racemic
compound, on the other hand, may be defined as a
crystalline substance of homogeneous structure
which contains an equal proportion of two enantiomorphously
related isomerides.
“The relations holding between a mere mixture
of optical antipodes, a pseudo-racemic substance, and
a racemic compound, are closely parallel to those existing
between a crystalline mixture, an isomorphous
mixture, and a double salt. The crystallographic
methods, by which a double salt can be distinguished
from an isomorphous mixture, may be directly
applied to distinguish between racemic and pseudo-racemic
substances. Thus, according as the crystalline
substance obtained from a mixture of two salts
155resembles or differs from either of its components
crystallographically, it is regarded either as an
isomorphous mixture or a double salt; similarly,
an inactive externally compensated substance, which
closely resembles its active isomerides crystallographically,
is to be considered as pseudo-racemic,
whereas when the contrary is true, it is to be regarded
as racemic.”
The work of Kipping and Pope may be regarded
as having finally vindicated and substantiated the
law of Pasteur, that substances of enantiomorphous
molecular configuration develop enantiomorphous
crystalline structures, and that the crystal structures
assumed by enantiomorphously related molecular
configurations are themselves enantiomorphously
related.
This subject, the main results and principles of
which have now been elucidated, may well be closed
with a reference to an interesting case of enantiomorphism
and optical activity which the author has
himself investigated,[15] and which is very similar
to the case of the tartaric acids. It had been
previously shown[16] by P. F. Frankland and W. Frew,
that when calcium glycerate was submitted to the
fermenting action of the Bacillus ethaceticus one-half
only of the glyceric acid was destroyed, and that the
remaining half was optically active, rotating the
plane of polarisation to the right.
Now glyceric acid,
has manifestly one
156so-called asymmetric carbon atom (that is, a carbon
atom the four valencies of which are satisfied by
attachment to four different monad elements or
groups), that belonging to the CHOH group. There
are consequently two possible arrangements of the
molecule in space, probably corresponding to the two
optically active varieties, namely, those represented,
as far as is possible in one plane, as below, the
asymmetric carbon atom (not shown in the graphic
representation) being supposed to be at the centre
of the tetrahedron, which is usually taken to
represent a carbon atom with its four valencies.
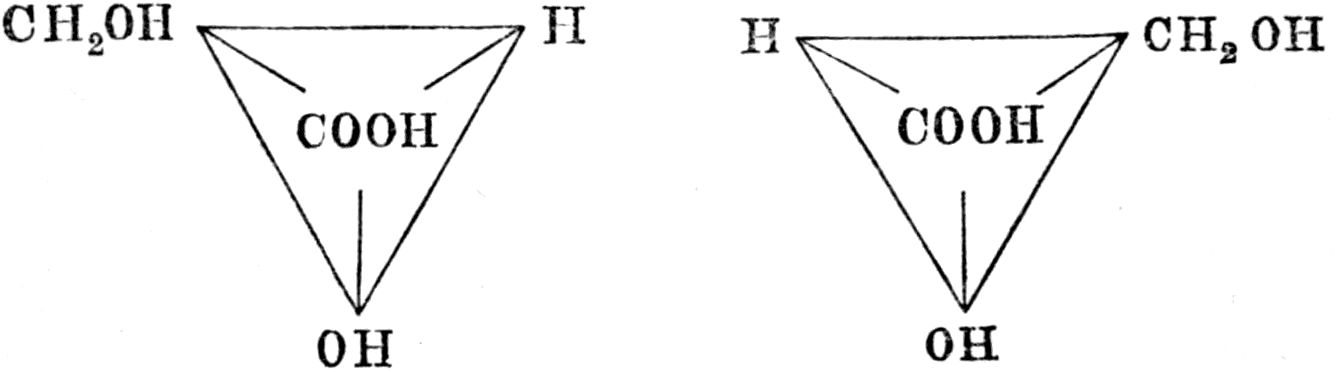
Dextro-glyceric acid itself proved to be an
uncrystallisable syrup, but the calcium salt,
Ca(C3H5O4)2.2H2O, was obtained in crystals sufficiently
well-formed to permit of a complete crystallographic
investigation, which the author undertook
by friendly arrangement with Prof. Frankland.
Although the acid itself is dextro-rotatory, aqueous
solutions of the calcium salt are lævo-rotatory to
the extent of –12.09 units of “specific rotation” for
sodium light.
The crystals were colourless well-formed prisms
which proved to be of monoclinic symmetry, the best
individuals being formed by very slow evaporation
of the aqueous solution. They were terminated at
both ends by pyramid and dome faces, and sometimes
157grew to the length of a centimetre. The actual
crystal elements found after a full series of measurements
were as under:—
CALCIUM DEXTRO-GLYCERATE.
Crystal system: monoclinic.
Class of Monoclinic System: sphenoidal or monoclinic-hemimorphic.
Habit: prismatic.
Monoclinic axial angle: β=69° 6′.
Ratio of axes: a : b : c = 1.4469 : 1 : 0.6694.
Forms observed:
| a = {100}, |
c = {001}, |
r′ = {̄201}, |
p = {110}, |
| m = {011}, |
o = {111} |
s = {̄1̄11}, |
n = {̄2̄11}. |
It will thus be seen that the system and the class
are precisely those of the two active tartaric acids,
which renders the case the more interesting. The
usual appearance of the crystals is shown in Fig. 65,
and the stereographic projection is given in Fig. 66,
which will elucidate the symmetry more clearly, the
plane of projection being the plane of symmetry
The latter, however, in this class is inoperative, the
two ends of the digonal symmetry axis, which runs
perpendicularly to the plane of the paper, being
differently terminated, as in the tartaric acids. The
faces of the forms o = {111} and m = {011} were never
found developed on the left side of the symmetry
plane, that is, on the left side of the crystal as drawn
in Fig. 65, the symmetry plane running perpendicularly
to the paper vertically from front to back;
they were only present on the right. Conversely,
the faces of s = {̄1̄11} and n = {̄2̄11} were never found
158developed on the right, but only on the left of the
plane of possible symmetry.
Moreover, it was frequently observed that the
right-hand faces (110) and (̄110) of the primary prismform
p were much more brilliant and truly plane
than those on the left hand, (1̄10) and (̄1̄10), which
were usually dull and often curved, as were also
frequently the faces of the left-hand forms s and n.
The right-hand distinguishing forms m and o, on
the contrary, were generally most brilliant and gave
admirable reflections of the goniometer signal-slit.
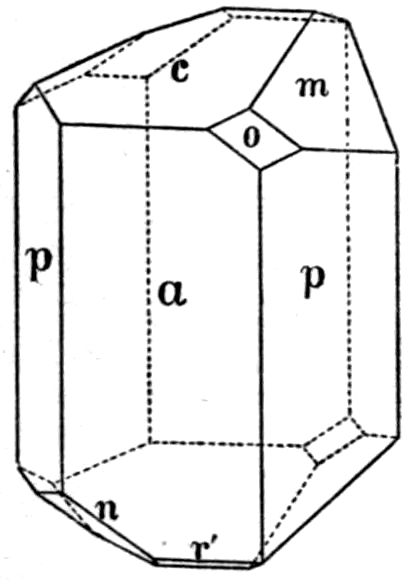
Fig. 65.—Crystal of Calcium Dextro-Glycerate.
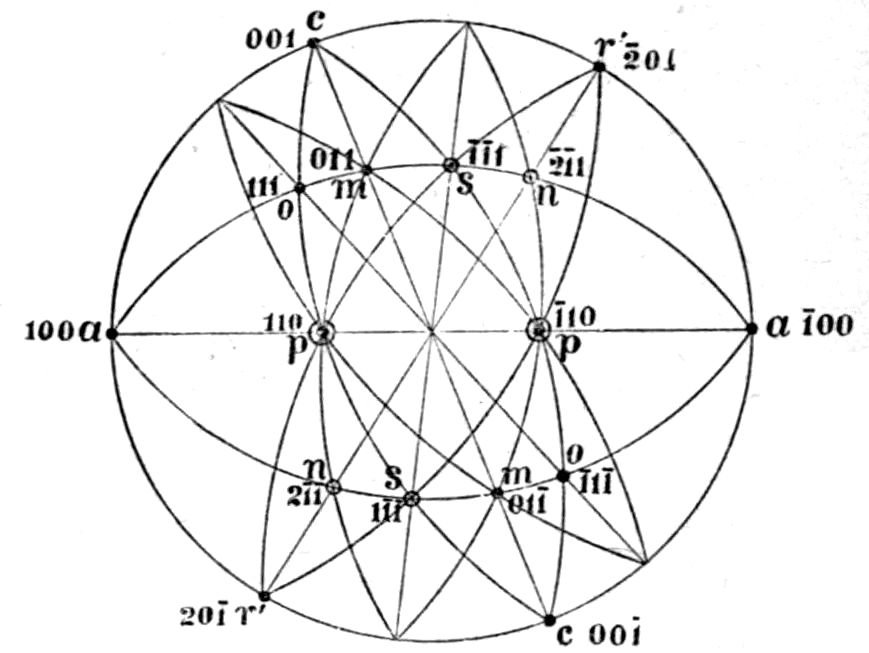
Fig. 66.—Stereographic Projection of Calcium Dextro-Glycerate.
The following table represents the results of the
angular measurements, twelve different well-formed
individual crystals having been employed. The
angles marked with an asterisk were the important
angles the mean observed values of which were
accepted as correct, being the best measured angles,
and which were therefore used as the basis of the
calculations.
| 159 |
| Table of Interfacial Angles of Calcium Glycerate. |
|---|
| |
|
|
|
|
|
|
| Angle measured. |
No. of measurements. |
Limits. |
Mean observed. |
Calculated. |
| {ap = 100 : 110 |
42 |
52° 32′ |
− |
54° 16′ |
53° 29′ |
* |
| {pp = 110 : ̄110 |
20 |
72 7 |
− |
73 33 |
73 4 |
73° 2′ |
| |
|
|
|
|
|
|
| {ac = 100 : 001 |
13 |
68 22 |
− |
69 42 |
69 3 |
69 6 |
| {cr′ = 001 : ̄201 |
13 |
52 4 |
− |
52 31 |
52 13 |
* |
| {r′a = ̄201 : ̄100 |
13 |
58 35 |
− |
58 46 |
58 41 |
* |
| |
|
|
|
|
|
|
| cm = 001 : 011 |
10 |
31 47 |
− |
32 19 |
32 3 |
32 2 |
| |
|
|
|
|
|
|
| r′n = ̄201 : ̄2̄11 |
2 |
29 43 |
− |
29 48 |
29 45 |
29 47 |
| |
|
|
|
|
|
|
| {ao = 100 : 111 |
7 |
53 59 |
− |
54 10 |
54 3 |
53 54 |
| {om = 111 : 011 |
7 |
18 20 |
− |
18 35 |
18 26 |
18 29 |
| {ma = 011 : ̄100 |
13 |
107 22 |
− |
108 24 |
107 41 |
107 37 |
| {an = ̄100 : ̄2̄11 |
11 |
62 32 |
− |
63 44 |
63 6 |
63 10 |
| {ns = ̄2̄11 : ̄1̄11 |
1 |
|
− |
|
21 35 |
21 27 |
| {sa = ̄1̄11 : 100 |
3 |
94 49 |
− |
95 34 |
95 18 |
95 23 |
| |
|
|
|
|
|
|
| {po = 110 : 111 |
9 |
43 51 |
− |
44 44 |
44 35 |
44 38 |
| {oc = 111 : 001 |
9 |
32 56 |
− |
33 15 |
33 7 |
33 7 |
| {cs = 001 : ̄1̄11 |
7 |
41 32 |
− |
43 2 |
42 10 |
42 17 |
| {sp = ̄1̄11 : ̄1̄10 |
7 |
59 15 |
− |
60 54 |
59 59 |
59 58 |
| {pc = ̄1̄10 : 00̄1 |
14 |
77 2 |
− |
78 21 |
77 42 |
77 45 |
| {cp = 00̄1 : 110 |
16 |
101 39 |
− |
103 36 |
102 16 |
102 15 |
| |
|
|
|
|
|
|
| {pm = 110 : 011 |
9 |
52 15 |
− |
53 25 |
52 42 |
52 41 |
| {mn = 011 : ̄2̄11 |
5 |
79 5 |
− |
79 26 |
79 15 |
79 12 |
| {np = ̄2̄11 : ̄1̄10 |
5 |
47 41 |
− |
48 23 |
48 4 |
48 7 |
| |
|
|
|
|
|
|
| {pr′ = 110 : ̄201 |
14 |
106 35 |
− |
108 42 |
108 5 |
108 1 |
| {r′p = ̄201 : ̄1̄10 |
26 |
70 54 |
− |
73 32 |
71 55 |
71 59 |
| {ps = ̄1̄10 : 1̄1̄1 |
5 |
66 42 |
− |
67 17 |
67 4 |
67 5 |
| {sr′ = 1̄1̄1 : 20̄1 |
6 |
40 36 |
− |
41 29 |
41 5 |
40 56 |
| |
|
|
|
|
|
|
| pm = ̄110 : 011 |
3 |
75 5 |
− |
76 21 |
75 37 |
75 45 |
There is a moderately good cleavage parallel to the
basal plane c = {001}.
The optical properties afford conclusive proof of
the monoclinic nature of the symmetry. The plane
of the optic axes is perpendicular to the possible
symmetry plane, b = {010}, and the first median line
160makes an angle of 23° with the vertical axis c, emerging
consequently nearly normal to the basal plane
c = {001}, so that a section-plate parallel to the c-faces,
or a tabular crystal or cleavage plate parallel to c,
shows the optic axial rings and brushes well. The
values of the apparent optic axial angle in air, 2E,
and of the true optic axial angle within the crystal,
2Va, the latter measured with the aid of a pair of
accurately ground section-plates perpendicular to the
first and second median lines and immersed in oil,
are given in the next table.
|
|
|
2E |
2Va |
| For |
lithium |
light |
51° 35′ |
34° 56′ |
| „ |
sodium |
„ |
52° 30′ |
35° 28′ |
| „ |
thallium |
„ |
53° 50′ |
36° 16′ |
The intermediate refractive index β was found to
be as under—
| For |
red lithium light |
1.4496 |
| „ |
yellow sodium „ |
1.4521 |
| „ |
green thallium „ |
1.4545 |
The double refraction was also determined and
found to be of positive sign.
The optical properties of calcium dextro-glycerate
thus confirm absolutely the monoclinic nature of the
symmetry, as regards the crystal system. And it
was conclusively demonstrated by the goniometrical
part of the investigation that the exterior symmetry
was not such as agreed with holohedral monoclinic
symmetry, but with that of the sphenoidal class, in
which the only one of the two elements of monoclinic
symmetry (the plane of symmetry and the digonal
axis of symmetry) in operation is the digonal axis,
thus leaving the two terminations of that axis,
161at opposite sides, right and left, of the possible
symmetry plane, unsymmetrical. And this is precisely
the symmetry which is characteristic of an
enantiomorphous optically active substance.
Unfortunately, the corresponding lævo-salt has
not yet been obtained in measurable crystals, but
there can be no doubt that whenever such are forthcoming
they will display enantiomorphism in the
precisely opposite and complementary sense, the
facial forms characteristic in this dextro-salt of the
right termination of the digonal axis being absent
on that side of the systematic symmetry plane but
developed on the left side instead, and vice versa,
and that the two enantiomorphous forms will together
make up the whole of the faces required by the full
symmetry of the monoclinic system.
A concrete instance like this, worked out practically
in the laboratory, brings home the precise nature
of this interesting relationship, between crystallographic
and molecular enantiomorphism on the one
hand and optical activity on the other hand, in a
particularly clear and forcible manner. It is hoped
that this brief account of it will also consequently
have been of assistance to the reader, in more clearly
appreciating the main points of this chapter.
162
CHAPTER XII
EFFECT OF THE SYMMETRY OF CRYSTALS ON THE PASSAGE OF LIGHT THROUGH THEM. QUARTZ, CALCITE, AND GYPSUM AS EXAMPLES.
The action of transparent crystals on the rays of
light which they transmit is a subject not only of the
deepest interest, but also of the utmost importance.
For it is immediately possible to detect a cubic
crystal, and to discriminate between two groups,
optically uniaxial and biaxial respectively, of the
other six systems of symmetry, three systems going
to each group, by this means alone. For a cubic
crystal is singly refractive in all directions. A
60°-prism, for instance, cut from a cube of rock-salt,
for the purpose of obtaining the refractive index of
the mineral by the ordinary method of producing a
spectrum and arranging it for minimum deviation of
the refracted rays, affords but a single spectrum, or a
single sharp image of the spectrometer slit when the
latter is fed by pure monochromatic light instead
of ordinary white light. This is true however the
prism may have been cut, as regards its orientation
with respect to the natural crystal faces.
But a 60°-prism cut from a crystal belonging to the
optically biaxial group, composed of the rhombic,
monoclinic, and triclinic systems of symmetry, will
always afford two images of the slit or two spectra,
163corresponding to two indices of refraction; and, when
the orientation of the prism is arranged so that the
refracting angle is bisected by a principal plane of the
ellipsoid which represents the optical properties, and
the refracting edge is parallel to one of the principal
axes of the optical ellipsoid, the prism, when arranged
for minimum deviation of the light rays, will at once
afford two of the three refractive indices, α, β, γ, corresponding
to light vibrations along two of the three
principal axial directions of the ellipsoid. The two indices
which the prism affords will be (1) the one which
corresponds to vibrations parallel to the refracting
edge, and (2) that which corresponds to undulations
perpendicular to the edge and to the direction of
transmission of the light through the prism (the third
axis of the ellipsoid). For the vibrations of the light
in the two rays into which the beam is divided on
entering the crystal are both perpendicular to the
direction of transmission and to each other; the two
images or spectra produced owing to the double
refraction, that is, owing to the different velocities
of the two mutually rectangularly vibrating rays,
thus correctly afford the means of determining two
of the three principal (axial) refractive indices.
Gypsum, the monoclinic hydrated sulphate of
lime, CaSO4.2H2O, already referred to in connection
with the Mitscherlich experiment in Chapter VII.,
is an excellent substance to employ for the demonstration
of this fact, by cutting and polishing a
60°-prism out of a clear transparent crystal of the
mineral as above described; and if a Nicol prism be
introduced in the path of the rays, one spectrum or
monochromatic image will be extinguished when the
164Nicol is arranged at its 0° position, and the other
when the Nicol is rotated 90° from this position.
This proves that the two rays affording the two
refractive indices are polarised in planes at right
angles to each other, and, moreover, enables us to
verify that the planes in which the vibrations of
the two rays occur are actually parallel and perpendicular
respectively to the refracting edge of the
prism. For the two extinctions occur when the
vibration plane of the Nicol is either vertical,
parallel to the prism edge, or horizontal, perpendicular
thereto.
If a second prism be cut complementarily to the
first, that is, so that the refracting edge is parallel
to the third axis of the ellipsoid (the direction of
transmission through the first prism) and the bisecting
plane again parallel to one of the three axial
planes of the ellipsoid, such a prism will also yield
two refracted images corresponding to two indices;
one of them, that particular image the vibrations of
which are parallel to the refracting edge, will correspond
to that one of the three principal indices which
was not given by the first prism, while the other one
will afford a duplicate determination of one of the
two indices afforded by the first prism. Hence, a
couple of such axially orientated prisms of a rhombic,
monoclinic, or triclinic crystal will enable us to determine
all three refractive indices, and one of them in
duplicate, which latter fact will enable us to check
the accuracy of our work.
If the 60°-prism be cut from a crystal of the uniaxial
group, that is, from a hexagonal, tetragonal, or
trigonal crystal—quartz or calcite being admirable
165examples of the latter and particularly suitable for
demonstration purposes—it will generally afford
two spectra in the same manner as a crystal of the
three birefringent systems of lower symmetry. But
there is one special mode of cutting which results
in the prism exhibiting only a single spectrum,
namely, when the hexagonal, tetragonal, or trigonal
axis of symmetry, which is also the unique “optic
axis” of the crystal along which there is no double
refraction, is arranged to be perpendicular to the
bisecting plane of the 60°-prism. For then the light
is transmitted along this unique axial direction
when the prism is arranged for the minimum
deviation of the refracted rays out of their original
path, and as it may vibrate in any direction
perpendicular thereto with equal velocity there is
no separation into two rays, that is, no double
refraction, and thus only a single spectrum is afforded
by such a prism in white light, or a single image of
the slit in monochromatic light, and this latter will
at once yield the refractive index which is generally
indicated conventionally by the letter ω, corresponding
to light vibrations perpendicular to the axis.
Spectroscopists take advantage of this interesting
fact, when they employ a train of quartz prisms so
cut in order to explore the violet and ultra-violet
region of the spectrum; for quartz transmits many
of the ultra-violet rays which glass absorbs. Each
prism gives only a single image like glass, whereas if
it were otherwise cut it would give two spectra,
which would so complicate matters as to render
quartz useless for the purpose.
When the prism of quartz or calcite, or of any
166hexagonal, tetragonal, or trigonal substance, is cut
so that the rays of light are transmitted through it
perpendicularly to the axis, and so that the refracting
edge is parallel to the axis, the light is broken up
into two rays, one of which is composed of light
vibrating parallel to the edge and therefore to the
axis, and the other of light vibrating perpendicularly
to the axis. Such a prism consequently affords the
two principal extreme refractive indices of the
crystal, ω and ε, the latter letter being always
assigned to the refractive index of a uniaxial crystal
corresponding to vibrations parallel to the axis.
A uniaxial crystal, one belonging to the hexagonal,
tetragonal, or trigonal systems, has thus two principal
refractive indices, ω and ε, while a biaxial
crystal, one belonging to the rhombic, monoclinic,
or triclinic systems of symmetry, has three, α, β,
γ, corresponding to vibrations respectively parallel
to the three rectangular axial directions of the
optical ellipsoid, which are also the crystallographic
axial directions in the case of a rhombic crystal.
The index α is the minimum, and γ the maximum
refractive index,the β index being intermediate; when
the latter lies nearer to α in value, the crystal is said
to be a positive one, but when nearer to γ the crystal
is conventionally supposed to be negative. Similarly,
when in a uniaxial crystal ε is the greater, as it is in
the case of quartz, the crystal is termed positive, but
if ω be the greater index, as happens in the case of
calcite, then the crystal is by convention considered
negative.
Just as in the case of gypsum, which is a positive
biaxial crystal (the reason for the term biaxial will
167presently be more fully explained), when the two
spectra afforded by a prism of calcite or quartz cut
to afford both ε and ω are examined in plane
polarised light, by introducing a Nicol prism somewhere
in the path of the light, the two images
corresponding respectively to ε and ω will be found
to be produced by light polarised in two planes at
right angles to each other. For when the Nicol is
at its 0° position one will be extinguished, and when
it is at 90° the other will be quenched. At the 45°
position of the Nicol both images will be visible with
their partial intensities, as happens also in the cases
of biaxial prisms.
This behaviour of 60°-prisms of crystals belonging
to the seven different styles of crystal architecture,
as compared with a prism of glass or other transparent
non-crystalline substance, is extremely
instructive. For not only is the optical constant
refractive index—the measure of the power exhibited
by the crystal of bending light, corresponding to its
effect in retarding by the nature of its internal structure
the velocity of the light vibrations—the most
important of all the optical constants, but also in
the course of its determination we learn more of the
behaviour of crystals towards light than from any
other type of optical experiment.
168

Fig. 67.—Experiment to show Rectangular Polarisation of the two Spectra afforded by a 60°-Prism of a Doubly Refracting Crystal cut to afford two Indices of Refraction.
In Fig. 67 is shown a convenient mode of demonstrating
the experiment with the aid of the electric
lantern and one of the large Nicol prisms of the
projection polariscope, already briefly described in
Chapter VII. in connection with the Mitscherlich
experiment. The 60°-prism is arranged on a small
adjustable stand nearest the screen; then comes
the Nicol polarising prism of 2½ to 3 inches clear
aperture, behind which is the projecting lens, at the
focus of which is placed the adjustable slit on a
separate stand. The slit is filled with light from the
condenser of the electric lantern, and in the lantern
front a thick water cell is arranged, in order to
remove sufficient of the heat rays which accompany
the light beam to avoid damage to the balsam joint
of the calcite Nicol. When all the parts are properly
arranged a sharp image of the slit should first be
thrown on the screen directly, in the temporary
absence of the 60°-prism, and then on replacing the
latter at the proper angle for minimum deviation,
169when the light traverses the prism parallel to its
third unused side, a spectrum or pair of spectra—according
to the position of the Nicol and to the
nature of the 60°-prism as explained in the foregoing
discussion of the possibilities—will be projected
on a second screen (or the same one if movable)
arranged at the proper angle to receive the refracted
rays.
If a single spectrum be afforded, which remains
single on rotation of the Nicol, the prism is of glass or
of a uniaxial crystal cut so that the light passes along
the optic axis. If two spectra be shown when the
Nicol is arranged in the neighbourhood of its 45°
position, the crystal is a doubly refracting one, and
if orientated so that the single optic axis, if the
crystal be uniaxial, is parallel to the refracting edge,
or, if the crystal be biaxial, so that the refracting edge
is parallel to one of the three principal axes of the
optical ellipsoid and its bisecting plane is parallel not
only to this but also to a second principal axis, then
one spectrum, corresponding to one principal refractive
index, will extinguish when the Nicol is rotated
to its 0° position, and the other spectrum, corresponding
to a second principal refractive index, will be
quenched on rotation of the Nicol to its 90° position.
The separation of the two spectra on the screen
depends on the amount of the double refraction, and
in the case of calcite this is exceptionally large, so that
the two spectra are widely separated on the screen.
They differ also considerably in dispersion. In the
case of quartz the double refraction is very small,
and the spectral images of the slit are consequently
so close together as almost to touch one another.
170The pair of spectra afforded by gypsum are similarly
very close together, owing also to weak double refraction.
The amount of the double refraction is
measured by the difference between the uniaxial
indices ε and ω, or that between the minimum and
maximum biaxial indices α and γ. The two spectra
given by quartz and calcite will correspond to ε and
ω, and the greatest separation of spectra occurs in
the case of gypsum when the spectra are those corresponding
to α and γ, and not to α and β or β and γ.
It will now be useful and very helpful to examine
more closely into the nature of the beautiful mineral
quartz, in order that a series of interesting experiments
may be described with it, which will assist
largely in rendering the optical characters of crystals
clear to us.
Quartz, rock-crystal, although perhaps the commonest
and best known of all crystallised substances,
the naturally occurring dioxide of silicon SiO2, is
yet one of the most remarkable and fascinatingly
interesting. To begin with, as explained in the last
chapter, quartz belongs to one of the eleven enantiomorphous
classes of lower than full systematic
symmetry, those which exhibit two mirror-image
forms related to one another like a pair of gloves.
The particular class of the eleven to which quartz
belongs is the trapezohedral class of the trigonal
system, and two typical left-handed and right-handed
crystals are shown in Fig. 68 and Fig. 69
respectively.
There is one principal form which is common to
both the hexagonal and trigonal systems, namely,
the hexagonal prism, and this is the chief form
171exhibited by quartz crystals. They are terminated
by an apparently hexagonal pyramid, but which
really consists of a pair of complementary rhombohedra,
which are purely trigonal forms; three upper
faces of each rhombohedron are developed at one
end of the prism which may be regarded as the upper,
and the three lower faces of each of the two individual
rhombohedra likewise at the lower end of a fully
developed doubly terminated crystal. The rhombohedron
is the characteristic form of the trigonal
system of crystal symmetry, the systematic crystallographic
axes being parallel to its edges. It is like
a cube deformed by extension or compression along
a diagonal, which latter is arranged vertically,
and becomes the trigonal axis of symmetry (not a
crystallographic axis), as shown in Fig. 70.
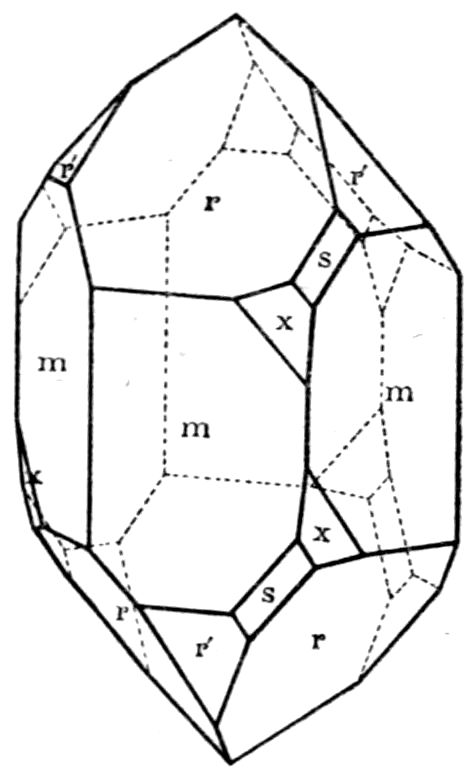
Fig. 69.
Left-handed and Right-handed Crystals of Quartz.
When two rhombohedra are equally developed, one
being rotated with respect to the other 60° round
the vertical trigonal axis of symmetry, they together
172resemble a hexagonal pyramid, and crystals of quartz
thus terminated at both ends are not uncommon,
so that at first sight a quartz crystal might be mistaken
for a hexagonal prism doubly terminated by
the hexagonal pyramid, and the mineral considered,
in error, to belong to the hexagonal system.
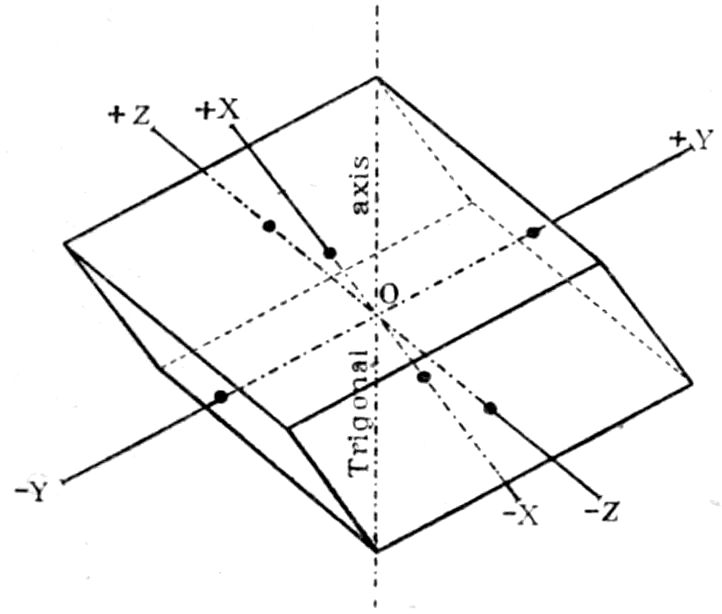
Fig. 70.—The Rhombohedron and its Axes.
But one alternate set of three faces of the hexagonal
pyramid at one end, and the oppositely alternate
set of three similar faces at the other end, will
usually be found to
be much less brilliant
(indeed often quite dull)
than the other alternate
three, and very frequently
also the amount
of development is
markedly different, both
facts indicating that the
terminal faces belong to
two different but complementary
rhombohedral
forms, and that the system of symmetry is the
trigonal and not hexagonal.
But there is much stronger evidence than this for
trigonal symmetry. For the little faces marked
s and x on Figs. 68 and 69 are characteristic of the
trapezohedral class of the trigonal system, and it
will be observed that on one crystal, Fig. 68, these
faces occupy and modify a left-hand corner or solid
angle on the crystal, while on the other crystal, Fig.
69, they occupy and replace a right-hand solid angle.
Now, if a plate be cut out of the former crystal perpendicularly
to the axis of the hexagonal prism, that
173is, to the optic axis of the trigonal uniaxial crystal,
it will be found to rotate the plane of polarisation
to the left, the direction in which the small faces
are situated; while if a similar plate be cut out of the
right-handed crystal shown in Fig. 69, that is, one
which has the small faces on the right, it will be
observed to rotate the plane of polarisation to the
right.
As quartz possesses the symmetry of the trigonal
system and is thus optically uniaxial, its optical
properties are expressed, in common with those of all
trigonal, tetragonal, and hexagonal crystals, by an
ellipsoid of revolution, an ellipsoid the section of which
perpendicular to the principal axis—that of revolution,
the maximum or minimum diameter of the
ellipsoid—is a circle. The optical properties are
consequently the same in all directions round this
axis, which has already been referred to by its
common appellation of the “optic axis.”
The optic axis is identical in direction with the
trigonal axis of symmetry in the case of quartz or
other trigonal crystal, and in the cases of hexagonal
and tetragonal crystals with the axes of hexagonal
and tetragonal symmetry, these three axes of specific
symmetry being the distinctive property of these
three respective systems, which are thus known in
common as optically “uniaxial.”
Consequently, no double refraction is suffered by a
ray transmitted parallel to the optic axis, and the
refractive index is equal in all directions perpendicular
to the optic axis, that is, for all rays vibrating
perpendicularly to the axis; hence the value of the
refractive index obtained along any such direction
174is one extreme value for the whole crystal, and as
already mentioned is distinguished by the letter ω.
The refractive index along the direction of the axis
itself is the other extreme value, and is labelled ε.
It must be clearly appreciated, however, that it is
not the direction of transmission but that of vibration
perpendicular thereto, that is meant when it is
said that, for instance, the direction of the axis
corresponds to the index ε. That is to say, a ray the
vibrations of which occur parallel to the optic axis of
a uniaxial crystal is refracted to an amount which
corresponds to the refractive index ε, while a ray
the vibrations of which occur perpendicularly to the
axis affords ω. The difference between ε and ω is
the measure of the double refraction of the crystal.
In the case of quartz ε is the greater, being 1.5534
for sodium light, quartz being thus positive according
to the convention already alluded to; while ω is the
smaller, namely, 1.5443. In the case of the other
widely distributed trigonally uniaxial mineral calcite,
carbonate of lime CaCO3, the opposite is the case, ω
being the greater, having the value 1.6583 for sodium
light, and ω the less, namely, 1.4864, calcite being thus
a negatively uniaxial substance. The amount of the
double refraction in the cases of the two minerals is
very different, ε-ω for quartz being 0.0091, and
ω-ε for calcite being as much as 0.1719.
Calcite is indeed a mineral endowed with an especially
large amount of double refraction, a property which renders it so
eminently suitable for use in demonstrating the
phenomenon, and for the construction of the Nicol
polarising prism, in which one of the two mutually
perpendicularly polarised rays, that which affords
175the index ω, is got rid of by total reflection at a
balsam joint, a large rhomb of calcite being cut in
half along a particular diagonal plane and the
two halves cemented together again with Canada
balsam; the other ray, which affords ε (but not
at its minimum value), is transmitted as a beam
of perfectly polarised light.
The result of this difference in the amount of the
double refraction of the two minerals quartz and
calcite is very interesting as regards their behaviour
with polarised light. A thin plate of quartz, such as
is often found in the slices of rock sections employed
for microscopic investigation, of muscovite granite
or quartz porphyry for instance, and which is usually
about one-fiftieth of a millimetre in thickness, shows
brilliant colours in a parallel beam of polarised light,
the Nicol prisms of the polarising microscope being
crossed for the production of the dark field before the
introduction of the section-plate on the stage. This
is only true, however, when the plate has not been cut
perpendicularly to the axis, for such a thin plate thus cut
does not perceptibly affect the dark field, there being
no double refraction of rays transmitted along the
axis, and the interference colours afforded by crystal
plates in polarised light being due to the interference
of the two rays produced by double refraction, one
of which is retarded behind the other so as to be in
a different phase of vibration. Also, the plate, even
when cut obliquely, and best of all parallel, to the axis,
has to be rotated in its own plane (perpendicular to
the optical axis of the microscope), to the favourable
position for the production of the most brilliant
colour. This especially favourable position is halfway
176between (at 45° to) the positions at which darkness
is afforded by the plate. For on rotating the
plate between the crossed Nicols it becomes four
times dark during a complete revolution, and at
places exactly 90° apart, known as the “extinction
positions,” whenever, in fact, that plane perpendicular
to the plate which contains the optic axis is
parallel to the plane of polarisation of either the
polarising or analysing Nicol. At the intermediate
45° positions the maximum colour is produced.
The colour owes its origin, as already mentioned,
to the interference of the two rays, corresponding to
the two refractive indices, into which the light is
divided on entering the crystal in any direction except
along the axis. For one of the rays is retarded
behind the other owing to the difference in velocity
which is expressed reciprocally (inversely) by the
refractive indices, and thus a difference of phase is
produced between the two light-wave motions, with
the inevitable result of interference when the vibrations
have been reduced to the same plane by the
analyser; light of one particular wave-length is then
extinguished, and the plate therefore exhibits a tint
in which the complementary colour to that extinguished
predominates. The light which leaves the
polarising Nicol is vibrating in one plane, but on
reaching the crystal this is resolved into two rays
vibrating at right angles to each other, and at 45°
on each side of its previous direction of vibration,
supposing the crystal to be arranged for the production
of most brilliant colour. On reaching the
analysing Nicol, the function of which is to bring the
two vibrations again into the same plane, these two
177rays are each separately resolved back to the planes of
vibration of the two Nicols, and that pair (one from
each ray) vibrating parallel to the analysing Nicol are
transmitted, while the other pair are extinguished.
The two former rays thus surviving, one individual ray
of the two having one refractive index and the other
individual the other index, are thus in a position to
interfere; for they are composed of vibrations in the
same plane and of practically the same intensity,
and differ only in phase. Extinction occurs when this
amounts to half a wave-length, or an odd multiple
of this, to which, however, requires to be added half
a wave difference of phase which is introduced by
the operation of the analyser. This explanation is
a general one, applicable to thin plates of crystals
belonging to all the six systems of symmetry other than
the cubic. For plates of the latter, unless they are in
an abnormal condition of strain, do not polarise.
When we take a plate of calcite of the same small
thickness as that of the quartz in a rock section,
thinner than a sheet of thin paper, we find that the
calcite does not polarise. So great is the retardation
of one of the two rays behind the other in calcite,
that a plate excessively thin is required in order that
colour shall be observed. For the colours of crystal
plates under the polariscope, due to double refraction,
are subject to the same laws as the colours of
thin films, namely, that as the thickness increases—introducing
more and more retardation in the case of
a crystal, just as in a thin film greater length of path
is introduced with increase of thickness—the
various tints of all the seven orders of Newton’s
spectra are exhibited in turn, each spectrum differing
178by one further wave-length of retardation, and
after the seventh the white of the higher orders
(white light mixed with colour, the latter thus appearing
only as a faint tint) gives place to true white
light, colour being no longer perceptible. Hence
with calcite, owing to the extremely powerful double
refraction, and therefore very considerable retardation
of the slower ray behind the quicker, a plate a
fiftieth of a millimetre only in thickness already
shows the white of the higher orders, that is, appears
only very feebly tinted with colour, and a plate of
calcite very much thinner still is required to show
brilliant colours. A plate of calcite, therefore, cut
obliquely or parallel to the optic axis, of the thickness
of a rock section or thicker, simply appears four
times dark and four times light alternately, at
positions 45° apart, as the section-plate is rotated
in its own plane perpendicular to the axis of the
polariscope.
When a plate of either quartz or calcite one-fiftieth
of an inch thick, cut perpendicularly to the optic axis,
is examined under the polariscope or polarising
microscope, the dark field is unaffected by its introduction
on the stage, remaining dark on a complete
rotation of the crystal plate in its own plane.
Moreover, the calcite plate continues to behave
similarly however much the thickness is increased,
the field remaining dark. But when quartz is examined
as regards the effect of thickness an extraordinary
thing happens. As the plate is thickened,
that is, as a series of plates of gradually increasing
thickness are successively placed on the stage, the
dark field begins to brighten, and eventually colour
179makes its appearance. Moreover, rotation of the
plate in its own plane—supposing the latter to be
strictly perpendicular to the axis of the polariscope and
the plate itself to have been truly cut perpendicularly
to the optic axis of the quartz crystal—produces no
change whatever, the colour remaining the same and
evenly distributed over the plate, thus differing from
the previous phenomena of interference due to double
refraction. When monochromatic light is employed,
yellow sodium light for instance, it is found that if
the plate be not too thick, say a millimetre in thickness,
the dark field is restored when the analyser is
rotated in a particular direction, either to the right
or to the left, for a specific angle, which is 21° 42′ for
a plate of quartz one millimetre thick. Moreover,
if the plate has been cut from a crystal showing the
distinctive trapezohedral-class faces s and x on the
right (Fig. 69) the analysing Nicol requires to be
rotated to the right; whereas if the plate has been
cut from a crystal showing these little determinative
faces on the left (Fig. 68) the analyser has to
be rotated to the left in order to quench the light.
It is obvious, therefore, that the colours of these
thicker plates of quartz are due to the phenomenon
of “optical activity.” The original plane of polarisation
of the light received from the polarising Nicol
is rotated by the quartz plate, and to an extent which
is directly proportional to the thickness. When
white light is used a particular colour is extinguished
for each position of the analyser, and the complementary
colour therefore predominates in the tint
actually exhibited. Now the most intensely luminous
part of the spectrum is about wave-length 0.000550
180millimetre in the yellow, and in the case of a plate of
quartz 7.5 millimetres thick this colour is extinguished
when the Nicols are crossed, while a plate of half this
thickness, 3.75 mm., actually exhibits the colour
under crossed Nicols and extinguishes it under parallel
Nicols. For the angle of rotation of the plane of
polarisation for light of this wave-length is 90° for a
plate 3.75 mm. thick, so that the analyser has to be
turned through a right angle from the crossed position,
that is, placed parallel to the polariser, in order
to extinguish this colour. A plate of double the
thickness, 7.5 mm., will require the analyser to be
rotated through 180°, the angle of rotation for this
thickness of plate, in order to extinguish this yellow
ray. But 180° rotation simply brings the Nicol
again to the crossed position, so that no rotation is
really necessary at all.
Now the complementary colour to the yellow of
wave-length 0.000550 mm. is the transition violet
tint, the well-known “tint of passage” between the
brilliant red end of the first order spectrum of Newton
and the deep blue of the beginning of the second
order. Hence, this violet tint is afforded by a plate
of 7.5 mm. thickness when the Nicols are crossed, and
by a plate of 3.75 mm. thickness when they are
parallel. When, therefore, these plates are examined
respectively under crossed and parallel Nicols, and
the analysing Nicol is turned ever so little, the tint
changes remarkably rapidly into brilliant red or
blue, according to the direction of the rotation of the
Nicol and the nature, whether right or left-handed,
of the quartz. Moreover, when two complementary
plates of each thickness are thus examined, one of
181each pair being cut from a right-handed crystal and
the other from a left-handed one, the colour will be
red in one case and blue in the other for the same
direction of rotation of the analyser.
A composite plate is frequently found very useful
in work in connection with optical rotation, and is
known as a “biquartz,” two plates of opposite
rotations being cemented together by Canada balsam,
the plane of junction being made perpendicular to
the plate so as to be almost invisible when the plate is
examined normally. When polarised light is employed,
the least rotation of the analyser from exact
crossing with the polariser, for which the violet
transition tint is evenly produced over the whole
composite plate, causes the half on one side of the
plane of junction (appearing as a fine line) to turn red
and the other half to turn blue or green.
This, in essence, is the nature of the optical
activity of quartz, and the secondary effects derived
from it influence all the optical phenomena afforded
by this interesting mineral. Owing to the fact
that quartz crystals are practically unendowed with
any facility for cleavage, the natural rhombohedral
cleavage being very imperfectly developed and
rarely seen, it is possible to cut, grind, and polish
large plates of this beautiful, colourless, and limpidly
transparent mineral without a trace of flaw. Such
quartz plates of large size, adequate to fill the field
of a large projection polariscope, the stage aperture
of which is nearly 2 inches in diameter, form
magnificent polarising objects for the projection on
the screen of the effects observed in polarised light.
As many of the optical properties of crystals may be
182illustrated with their aid, it is proposed in the next
two chapters to describe a few of the more interesting
screen experiments which can be performed with
quartz, first (Chapter XIII.) in convergent polarised
light, and then (Chapter XIV.) in parallel polarised
light, and thus to illustrate the facts relating to the
connection between optical activity and the internal
structure of crystals in a manner which will at the
same time be interesting and will lead to their much
clearer comprehension.
The experiments described are largely those with
which the author illustrated his lecture to the British
Association for the Advancement of Science during
their 1909 meeting at Winnipeg.
183
CHAPTER XIII
EXPERIMENTS IN CONVERGENT POLARISED LIGHT WITH QUARTZ, AS AN EXAMPLE OF MIRROR-IMAGE SYMMETRY AND ITS ACCOMPANYING OPTICAL ACTIVITY.
It has already been shown that crystals are optically
divisible into two classes characterised respectively
by single and by double refraction. Singly
refractive crystals belong exclusively to the system
of highest symmetry, the cubic. They afford
obviously only one index of refraction, which is
generally symbolised by the Greek letter μ, the
value of this constant being the same for all directions
throughout the crystal. Crystals of the other
six systems of symmetry are all doubly refractive.
Those of the trigonal, tetragonal, and hexagonal systems
have been shown in the last chapter to possess
two refractive indices, a maximum and a minimum,
one represented by ε corresponding to light vibrating
parallel to the singular axis of the system, the trigonal,
tetragonal, or hexagonal axis of symmetry,
and another signified by ω corresponding to light
vibrations perpendicular to that axis. For the
properties are identical in all directions around this
axis, which is thus the optic axis as well as the predominating
crystallographic one. Such crystals are
consequently known as “uniaxial.” When ε is the
larger refractive index the crystal is positive, while
184if ω be the maximum the crystal is said to be negative.
It has been shown in the last chapter that quartz
belongs to the positive category, while calcite is
negative. Along the one direction of the optic axis
these uniaxial crystals behave like singly refractive
crystals do in all directions.
Crystals of the rhombic, monoclinic, and triclinic
systems of symmetry have also a minimum refractive
index, symbolised by α, and a maximum index indicated
by γ, corresponding to light vibrating parallel
to two directions at right angles to each other; the
third direction perpendicular to both these and normal
to their plane does not afford an index of refraction
equal to either of these, however, as in the case of a
uniaxial crystal, but one of an intermediate value,
for which the second letter β of the Greek alphabet
is reserved. Whether this value β is nearer to the
minimum α or to the maximum γ determines the conventional
optical sign of the crystal, whether positive
or negative. In the case of the rhombic system the
three rectangular directions in question are identical
with the three rectangular crystallographic axes.
In the monoclinic system the single symmetry axis
normal to the unique plane of symmetry is identical
in direction with either the α, β, or γ optical
direction, but in the triclinic system there are no
coincidences between the crystal axes and those of
the optical ellipsoid. Along none of these axial
directions of the optical ellipsoid which can be
imagined to express graphically the refractive index—an
ellipsoid known as the optical “indicatrix,”
and which has been shown by Fletcher to be a more
convenient mode of expressing the optical characters
185of a crystal than the vibration-velocity ellipsoid of
Fresnel—do the optical properties resemble those of
a uniaxial crystal along the optic axis, or of a cubic
singly refractive crystal, the crystal being doubly
refractive along all three axes.
But it is a remarkable fact, nevertheless, that there
are two directions in such a crystal along which the
latter is apparently singly refractive, and these two
directions are known as the “optic axes,” and the
crystals of the three systems of lower symmetry
are consequently said to be “biaxial.” These two
singular directions are symmetrical to two of the
three rectangular axes of the ellipsoid, those corresponding
to the extreme indices α and γ, in the
plane containing which two axes they lie, and they
are perpendicular to the third β. For if we draw
the ellipse of which the minimum and maximum
axes are represented in length by α and γ, there will
obviously be four symmetrical positions on the curve
where a line drawn to the centre of the ellipse would
be equal to the intermediate value β. If we join
opposite pairs of these four points by diameters
(lines passing through the centre of the ellipse) we
have two directions each of which, together with the
perpendicular direction of the β axis, lies on a circular
section of the ellipsoid, for all radii from the centre
lying in each of these sections are alike equal to β.
Consequently, light transmitted along the two
directions in the crystal normal (perpendicular) to
these two circular sections will suffer no apparent
double refraction, the refractive index being the
same, namely β, and the velocity of vibration equal
in all directions in the crystal parallel to the two
186circular sections. Hence, we have two directions
in biaxial crystals in which the optical properties are
similar to those of uniaxial crystals along their
singular optic axis. But the optical properties
along the two optic axes of a biaxial crystal are
advisedly stated to be “similar” to, and not
“identical” with those along the optic axis of a
uniaxial crystal; for although they are identical to
all ordinary experimental tests, they are not quite
so when we come to ultimate details, which, however,
are beyond the purview of this book, but an account
of which will be found in the author’s “Crystallography
and Practical Crystal Measurement”
(Macmillan & Co., 1911).

Fig. 71.—Projection Polariscope arranged for Convergent Light.
With these prefatory theoretical remarks, which
are necessary in order that the experiments now to
187be described should be understood, we may proceed
to consider a graduated series of experimental
demonstrations which it is hoped will render clear
some of the more important features of crystal
structure which have been dealt with in previous
chapters. Our principal agent will be polarised
light, that is, light which has been reduced to
vibration in a single plane by means of the well-known
Nicol’s prism. This latter is a rhomb of
calcite which has been cut in two parts along a specific
diagonal direction, and the two parts of which have
been re-cemented together with Canada balsam,
in such a manner that one of the two rays, known as
the “ordinary” and which corresponds to the ω
refractive index, into which the doubly refracting
calcite crystal divides the ordinary light which it
receives from the lantern or other source of light, is
totally reflected at the layer of balsam, while the
other ray, known as the “extraordinary” and
corresponding to a refractive index of intermediate
value between ω and ε, and composed of vibrations
at right angles to those of the totally reflected ray,
is alone transmitted, as a ray of plane polarised light.
We employ a pair of such Nicol prisms (a very
large pair being shown in Fig. 71), together with
a convenient system of lenses for focussing either
the object-crystal or the phenomena displayed by
it, as a “polariscope,” which is the most powerful
weapon of optical research on crystals which has
ever been invented. When the two prisms are
arranged so that the vibration planes of the polarised
light which they would singly transmit are
parallel, we speak of them as “parallel Nicols,” and
188light is transmitted unimpeded through the pair
thus placed in succession; but when one of them is
rotated the light diminishes, until when the vibration
planes are at right angles no light escapes at all
if the Nicols are properly constructed, there being
produced what is known as the “dark field” of the
“crossed Nicols.” For the plane polarised light
reaching the analyser from the polariser cannot
get through the former, its plane of possible light
vibration being perpendicular to that of the already
polarised beam.
The phenomena exhibited by crystals in polarised
light are of two kinds, namely, those observed when
a parallel (cylindrical) beam of fight is passed through
the crystal, and those exhibited when a converging
(conical) beam of fight is employed and concentrated
on the crystal, the centre of which should occupy
the apex of the cone. The disposition of apparatus
in the former case of parallel light will be described
in the next chapter and illustrated in Fig. 79. The
arrangement for convergent light, as employed for
projections on the screen, has already been referred to
in connection with the Mitscherlich experiment with
gypsum, and illustrated in Fig. 51 (page 92). The
arrangement is shown again here for convenience,
in Fig. 71. The parts of the apparatus are briefly
as follows: (1) the electric lantern with self-adjusting
Brockie-Pell or Oliver arc lamp and a 4½ or 5–inch
set of condensers; (2) the water cell; (3) the polarising
Nicol with a parallelising concave lens at its
divided-circle end; (4) a condensing lens; (5) the
convergent system of three lenses closely mounted
in succession; (6) the crystal; (7) the collecting
189system of three lenses equal and similar to the
convergent system; (8) the field lens; (9) the projection
lens; and (10) the analysing Nicol. The
ten parts are separately mounted in the author’s
apparatus, which confers greater freedom in experimenting
and more power of varying the conditions;
the converging and collecting lens systems, however,
are mounted in a separately adjustable manner on a
common standard, which carries in the centre complete
goniometrical adjustments for the crystal.
When we place on the stage of the polariscope,
the Nicols being crossed, a plate of a uniaxial
crystal cut perpendicularly to the optic axis, and
subsequently a similar plate of a biaxial crystal cut
perpendicularly to that axis of the optical ellipsoid,
either α or γ, which is the bisectrix of the acute
angle between the two optic axes, and use the system
of lenses which converges the light rays received from
the polarising Nicol prism on the crystal, as shown in
Fig. 71, we observe in the two cases quite different
and very beautiful interference phenomena, which
at once distinguish a uniaxial from a biaxial crystal.
The two appearances are illustrated in Plate XIV.,
by Figs. 72, 73, and 74, which are reproductions
of the author’s direct photographs. Fig. 72 shows
the interference figure afforded by uniaxial calcite,
which is the same for all positions of the crystal plate
when rotated in its own plane by the rotation of the
stage. Figs. 73 and 74 represent the interference
figures given by biaxial aragonite, the orthorhombic
form of carbonate of lime, calcite and aragonite being
the two forms of this substance, which has been
shown in Chapter VII. to be dimorphous. The
190effect shown in Fig. 73 is afforded when the line
joining the two optic axes is parallel to the plane of
vibration of either of the crossed Nicols, and the interference
figure represented in Fig. 74 is given when
the stage and crystal (or the two Nicols simultaneously)
are rotated 45°.
The uniaxial calcite figure (Fig. 72) consists of
circular spectrum-coloured rings resembling the well-known
Newton’s rings, but with a dark cross, fairly
sharp near the centre but shading off towards the
margin of the field, marking the directions of the
vibration planes of the Nicols.
The biaxial aragonite figures (Figs. 73 and 74)
show two series of rings surrounding the two optic
axes and thus locating the positions of their emergence,
equidistant from the centre of the field, where
the bisectrix emerges. They are not circular, but
are curves known as lemniscates, which are complete
rings nearest to the two optic axes, but soon pass
into figure-of-eight loops, and eventually into ellipse-like
lemniscates enveloping both optic axes, and more
and more approaching circles in their curvature as
the margin of the field is approached. Moreover,
when the direction of the fine joining the two optic
axes is parallel to the vibration plane of either of the
Nicols, as was the case when Fig. 73 was produced
and photographed, a black rectangular cross is seen,
one bar, which is much the sharper one, passing
through the optic axes and the other lying between
them at right angles to the first bar, the centre of
the cross being in the middle of the field.

PLATE XIV.
Fig. 72.—Crystal Plate cut perpendicularly to the Axis.
Uniaxial Interference Figure afforded by Calcite (Trigonal) in Convergent Polarized Light, with Crossed Nicols.

Fig. 73.—Crystal Plate cut perpendicularly to the Bisectrix of the Acute Optic Axial Angle.
Biaxial Interference Figure afforded by Aragonite (Rhombic) in Convergent Polarised Light, with Nicols crossed and parallel to the Vibration Directions of the Crystal.

Fig. 74.—The same Plate as for the previous Figure.
The same when the two Nicols have been rotated in the same direction for 45°, still remaining crossed.
Characteristic Uniaxial and Biaxial Interference Figures in Convergent Polarised Light.
(Reproductions of direct Photographs by the author.)
191On rotating the crystal plate in its own plane,
while no change occurs with the calcite, the aragonite
figure changes as regards the black cross, which
breaks up into hyperbolic curves currently spoken of
as “brushes,” until when the plate has been rotated
45° the appearance is that shown in Fig. 74, the eye
being supposed to have followed the rotation. Or,
keeping the eye still, the effect shown in Fig. 74 is
equally produced by the simultaneous rotation of
both Nicols for 45°. The vertices of the hyperbolæ
now mark the positions of the optic axes, and the
angle between them is the apparent angle of the
optic axes as seen in air, which is considerably
different from the true angle between the optic
axes within the crystal, owing to the very different
refraction of light in air and in the crystal substance.
Now some crystals exhibit a very different optic
axial angle at different temperatures, and one of the
most beautiful experiments which have ever been
performed is the Mitscherlich experiment with
gypsum, which has already been described in
Chapter VII. in connection with the work of Mitscherlich,
and illustrated in Plate XII., Figs. 52 to 55.
Other substances, on the other hand, show a marked
change of optic axial angle as the wave-length of
the light is changed, and such a case has already
been described in Chapter VIII. and illustrated in
Plate XIII., Fig. 58. The figure afforded by such
a substance in ordinary white light is, however, a
complicated one, quite different from the normal
one of Fig. 73 afforded by aragonite, as will be
clear on reference to the interference figure shown
at f in Fig. 58, which represents the figure given
by ethyl triphenyl pyrrholone in white light.
In order to understand such biaxial interference
192figures thoroughly, they should be studied in monochromatic
light, when one obtains a clear and sharp
figure consisting of black curves as well as the cross
or brushes, and very sharp vertices to the brushes
when the crystal is arranged as in Fig. 74. The optic
axial angle can then be measured for each important
wave-length of light in turn, and the variation for
wave-length followed throughout the whole spectrum.
For this purpose it is very convenient to have a
source of monochromatic light of any or every wave-length
always at hand, and the author some years
ago devised a spectroscopic monochromatic illuminator,[17]
for use with any observing instrument, and
which is particularly convenient for use with the
polariscopical goniometer which is employed in
practice for the measurement of optic axial angles.
It is shown, along with the latter instrument, in
Fig. 75. The spectroscope has a single but very
large prism of heavy but colourless flint glass, and
the spectrum produced—the electric lantern being
the source of light, its rays being concentrated on
the slit—is filtered through a second slit at the
other end of the spectroscope, where the detachable
eyepiece is situated when the instrument is
used as an ordinary spectroscope, and for the calibration
(with the Fraunhofer solar lines) of the circle
on which the prism is mounted. The escaping narrow
slit of monochromatic light includes only the 250th
part of the spectrum, so is monochromatic in a high
sense of the word. It impinges on a little ground
glass diffuser carried in a very short tube in front of
this exit slit, and the optic axial angle polariscope is
193brought up almost into contact with the ground
glass, and is thus supplied with an even field of pure
monochromatic light. With this apparatus it is
easy to observe the exact crossing wave-length in all
cases of crossed-axial-plane dispersion such as that
illustrated in Fig. 58; for the reading of the graduated
circle on which the prism is mounted, and
which is rotated in order to cause monochromatic
light of the different wave-lengths in turn to stream
through the exit slit, affords the exact wave-length
with the aid of the calibration curve once for all
prepared. This calibration of the graduations is
readily carried out by using sunlight, and determining
the readings corresponding to the adjustment
of the principal Fraunhofer lines in the middle of
the exit slit.

Fig. 75.—Optic Axial Angle Goniometer and Spectroscopic Monochromatic Illuminator.
194Having thus rendered clear the nature of ordinary
interference figures afforded by crystals of the two
types, uniaxial and biaxial, in convergent polarised
light, we may pass on to see what happens when we
take a number of plates of quartz of different thicknesses,
cut perpendicularly to the optic axis in all
cases, instead of a plate of calcite. We will examine
first a fine pair of hexagonal quartz plates so cut, each
1 millimetre thick exactly, and about 2 inches
in diameter. One was cut from a right-handed
hexagonal prism, and the other from a similar left-handed
one.
Employing the lantern projection polariscope
shown in Fig. 71, arranged for convergent light just
as for the Mitscherlich experiment, and with the
Nicols crossed, we will now see what happens when
each of these plates in turn is placed at the focus of
the light rays, between the two convergent systems
of lenses. On the screen we observe in each case a
somewhat similar interference figure to that given by
calcite, a black cross and rainbow coloured circular
rings, the smallest ring, however, being very large
relatively to the innermost ring given by calcite, and
the other rings being also further separated from
each other. Moreover, the black cross appears
broadened out, this spreading of both rings and cross
being due to the thinness of the plate combined with
the low double refraction of quartz. Further, the
right-handed and left-handed plates both afford
apparently identical figures. In order to obtain a
sharp figure like that of calcite we require to add
a fourth lens, kept in reserve for such cases, to each
of the two similar convergent lens systems, one on
each side of the crystal plate, in order to increase
the convergence of the light rays. The figure then
obtained with one of the two plates is reproduced
in Fig. 76, Plate XV.

PLATE XV.
Fig. 76.
Interference Figure afforded by a Quartz Plate, 1 Millimetre thick, in strongly Convergent Polarised Light.

Fig. 77.
Interference Figure afforded by a Quartz Plate, 3·75 Millimetres thick, in moderately Convergent Polarised Light.

Fig. 78.
Interference Figure (Airy’s Spirals) afforded by two superposed Quartz Plates, 3·75 Millimetres thick, one of Right-handed Quartz and the other of Left-handed Quartz, in moderately Convergent Polarised Light.
Interference Figures in Convergent Polarised Light afforded by Quartz Plates cut Perpendicularly to the Axis.
195Let us now observe, however, what occurs when a
thicker plate of quartz is used. Taking one of 7.5 mm.
thickness, and placing it in the focus of the converging
rays, after removing the two extra lenses, we
see on the screen quite a different effect, an attempt
to reproduce which photographically in black and
white is made in Fig. 77 on the same Plate XV.
The rings are closer together (using the same degree of
convergence), and the innermost is smaller; moreover,
within it all signs of the central part of the black cross
have disappeared, and instead a brilliant violet colour
is shown, which alters to bright red of the first order
spectrum with the least rotation of the analysing
Nicol in one direction from its crossed position with
respect to the polarising Nicol, while if the rotation be
in the opposite direction the deep blue of Newton’s
second order is produced. The arms of the cross,
however, appear towards the margin of the field.
The violet colour shown for the exact position of
crossing of the Nicols is the tint of passage between the
first and second orders of Newton’s spectra, and this
illumination of the central part of the interference
figure is obviously the effect of the optical activity
of quartz, for the tint is the same as is produced
with the plate in ordinary parallel plane polarised
fight, and is, in fact, due to the central axial rays
of the convergent cone being practically parallel.
196On rotating the analysing Nicol for a few more
degrees to the right we observe that the innermost
ring widens out and that the red passes into orange
and yellow, the quartz plate being a right-handed
one. But when a similar plate cut from a left-handed
quartz crystal is used instead, the inner ring closes up
somewhat for the same rotation of the analyser,
moving inwards instead of outwards, and the blue
colour given with the first slight rotation passes into
green and yellow as the rotation is continued.
Moreover, the circular character of the rings is altered,
and so much so that when the rotation has proceeded
as far as 45° the shape of the rings has changed almost
to a square. These alterations in the interference
figure are characteristic of the two varieties of quartz
crystals. A useful rule to remember is, that for a
right-handed crystal rotation of the analyser to the
right causes the colours to appear in the order of their
refrangibility, namely, the least refrangible red first,
then orange, yellow, green, blue and violet in their
order; while for a left-handed crystal the converse
is true when the direction of rotation of the analyser
is the same, that is, to the right, clockwise; obviously
also the colours appear in the opposite order when the
rotation of the analyser is to the left.
It will now prove of interest to examine the effects
produced by two plates of opposite varieties of quartz
of half this thickness, namely, 3.75 mm. The
phenomena are very similar to those just described,
but the rings are a little wider, and the larger area
within the innermost ring is now filled with yellow
light instead of violet, when the analyser is exactly
crossed to the polariser. It passes into a bright
197green when the analyser is rotated slightly on one
side, and into orange when the Nicol is rotated in
the reverse direction. But the most interesting
thing of all is to observe what occurs when these two
plates of 3.75 mm. thickness, one of right-handed
quartz and the other of left-handed, are superposed
and placed in contact together as one plate, of
double the thickness, 7.5 mm., at the convergent focus.
A beautiful spiral figure is produced on the screen,
composed of the celebrated “Airy’s spirals” as if
the black cross were being reproduced in the central
part, but with each of its bars distorted into the shape
of the letter S, as shown in Fig. 78 at the foot of
Plate XV. The contrary effects of the two opposing
rotations are thus extraordinarily indicated visually in
the interference figure afforded by the composite plate.
Now, it is of great practical interest that certain
quartz crystals are found in nature which show
Airy’s spirals directly, on cutting a plate 7.5 mm.
thick or thereabouts, perpendicular to the optic axis.
For instance, one in the author’s collection of
quartzes, a single plate of an apparently homogeneous
and perfectly limpid crystal, shows the spirals exceedingly
well and clearly defined. As a matter of fact,
it is a twin, a right and a left-handed crystal being
twinned together with an invisible plane of composition,
which is only revealed on examining the
crystal in polarised light, as will be demonstrated in
the next chapter by the use of parallel polarised
light. The fact of such a plate of quartz affording
Airy’s spirals in convergent polarised light is, however,
of itself an excellent proof of the twinning of
two crystal individuals of the opposite varieties.
198Now the very shape of these spiral figures suggests
screw action of the molecular structure of the crystals
on the waves of light passing through them, and
moreover, of the action of two screws of opposite
directions of winding, one clockwise and the other
anti-clockwise, thus remarkably confirming the supposition
that the point-systems of the structure of
the right and left-handed varieties of quartz are of a
helical nature and respectively of opposite modes of
winding.
Another experiment, devised by Reusch, which still
further enhances the probability that this supposition
as to the structure of quartz crystals is correct, may
next be introduced. A thin film of biaxial mica has
been cut into twenty-four narrow strips, which have
been laid over each other at angles of 60°, so that a
screw-shaped pile has been formed of the central
overlapping parts, consisting of four complete rotations;
that is, there are four repetitions of the
“pitch” of the screw, each composed of six films.
On placing this composite plate of mica at the convergent
focus of the lantern polariscope, so that the
overhanging ends of any four identically superposed
strips occupy the focus, the ordinary biaxial interference
figure of mica—two sets of rings and hyperbolic
brushes, very much like Fig. 52, Plate XII.—is
observed on the screen. But when the plate is
moved so that the central part comes into the focus,
where all the twenty-four films overlap in their
six different orientations 60° apart, and so that all the
light rays have to traverse the whole helical pile of the
twenty-four films, a uniaxial figure exactly like that of
quartz is produced, namely, one composed of circular
199rings, with a black cross only visible, however, at the
marginal part, and with the inner ring filled with
brightly coloured light. Moreover, on slightly
rotating the analysing Nicol the innermost ring
moves outwards or inwards and the colour changes
to blue or red, according to the direction in which
the helix had been wound, in exact accordance
with the rule stated above for quartz.
If now a second such helical pile of mica films, but
one for which the opposite manner of winding has
been adopted, anti-clockwise if the first had been
clockwise, be examined at the convergent focus,
precisely the same appearance will be observed with
crossed Nicols, but the opposite changes will occur on
rotating the analyser. Finally, to complete the
interesting proof of the helical nature of quartz
crystals, when these two oppositely wound composite
mica plates are superposed—each being marked
carefully to indicate the direction of the helix and
the proper mode of superposition in order to effect
precise oppositeness of arrangement, mirror-image
symmetry, in fact, about the plane of contact—and
placed in the convergent beam near its focus, there
is at once seen on the screen a magnificent display of
Airy’s spirals, as perfect as those afforded by the
fine natural twin last experimented with. Hence,
there can be no doubt whatever that the remarkable
optical behaviour of quartz is due to its point-system
being of a helical nature, a right or a left-handed
screw structure being apparently produced in nature
with equal facility. The circumstances of environment
during the formation of the crystal probably
determine which variety shall be produced, and when
200the nature of the environment becomes changed
during the operation of formation either twins are
produced of the two varieties, or separate individual
crystals.
This may well conclude our experiments in convergent
polarised light, which—including the beautiful
Mitscherlich experiment described in Chapter
VII., of exhibiting the crossing of the optic axial
plane in the case of gypsum, and the production of all
the types of interference figures in succession, as the
crystal becomes warmed by the heat rays accompanying
the beam of convergent light—will have
introduced the reader to a typical series of such
experiments, and such as were actually exhibited by
the author to the British Association at Winnipeg.
We may pass, therefore, in the next chapter to the
consideration of an equally interesting series in which
a parallel beam of polarised light will be used, which
will still further elucidate the internal structure in
the especially instructive case of quartz crystals,
and that of crystals in general.
201
CHAPTER XIV
EXPERIMENTS WITH QUARTZ AND GYPSUM IN PARALLEL POLARISED LIGHT. GENERAL CONCLUSIONS FROM THE EXPERIMENTS WITH QUARTZ.
In order to rearrange the projection polariscope for
experiments in parallel light, we simply remove the
three lenses on separate stands (Fig. 71), and the
convergent systems of lenses on their special adjustable
stand with goniometrical crystal holder, from
between the two Nicol prisms, and replace them by
two other separately mounted lenses, acting together
as an achromatic projecting objective, and a
rotatable object stage. The whole arrangement as
thus altered for experiments in parallel polarised
light is shown in position in Fig. 79. The change is
readily made, a gap in the plinth-bed guides near
the analysing Nicol enabling it to be effected without
removing either of the prisms, the analyser being
simply drawn along a few inches nearer the end in
order to expose the changing gap. The pair of
lenses consists of a plano-convex lens of 5 inches
focus and 2¼ inches diameter, and another plano-convex
lens of 8½ inches focus and 2 inches aperture,
with their convex faces turned towards each other.
Together they produce on the screen an excellent
image of the object on the stage, and the size of the
image can be varied at will by regulating the relative
202positions of the two lenses with respect to each other
and to the object stage. If found more suitable for
the particular screen distance available, the 5–inch
lens may be replaced by a 6–inch lens also provided
as an alternative.
Fig. 79.—Projection Polariscope arranged for Parallel Light.
When the analysing Nicol is arranged with its
vibration direction parallel to that of the polariser,
we obtain bright light on the screen on actuating the
electric lantern, and the image of an object on the
stage can thus be projected on the screen on a bright
ground. But when the analyser is crossed to the
polariser, that is, rotated to the position 90° from
this parallel position, the two planes of vibration of
the Nicols being then at right angles, the screen is
quite dark. Before continuing in this dark field our
experimental study of quartz, which is obviously a
203type of the more exceptionally behaving substances
owing to its special structure, it will be wise to
examine a more ordinary kind of crystalline substance.
For this purpose gypsum—better known in
optical work as selenite, hydrated sulphate of lime,
CaSO4.2H2O, crystallising in beautifully transparent
and often large crystals belonging to the monoclinic
system, a typical one of which has been illustrated in
Fig. 9 (page 14), and which we have already referred
to in connection with the Mitscherlich experiment
described in Chapter VII.—is especially suitable, on
account of its clear and colourless transparency, the
large size of crystals available, and the brilliancy of
the polarisation colours which they afford when
adequately thin. A very perfect cleavage being
developed parallel to the symmetry plane, the
clinopinakoid {010}, such thin films, of even thickness
throughout, can be readily prepared.
Such a very thin cleavage plate, about 1½ inches in
its longest dimension, is mounted with Canada balsam
between a pair of circular glass plates 1⅞ inches in
diameter, the standard size of object plates for the
projection polariscope; the double plate is then supported
in a mahogany frame also of the standard size—4
by 2¼ inches, with clear aperture of 1⅝ inches
diameter and supporting rabbet for the plate 1⅞ to
2 inches diameter—on the rotating stage by a pair of
spring clips. The Nicols being arranged with their
vibration directions parallel, in order to permit
light to travel to the screen, and the lenses being
arranged properly for a sharply focussed picture of
suitable size, the outline of the crystal plate will be
seen on the screen, and the whole area of the crystal
204will either at once appear coloured, or will do so on
more or less rotation of the stage carrying the
crystal, which rotates the latter in its own plane.
The crystal outline is of the character shown in
Fig. 80, which also gives the positions of the crystal
axes a and c, and a simple stereographic projection
of the faces of the crystal, from which the nature of
the faces bounding the section-plate will be clear.
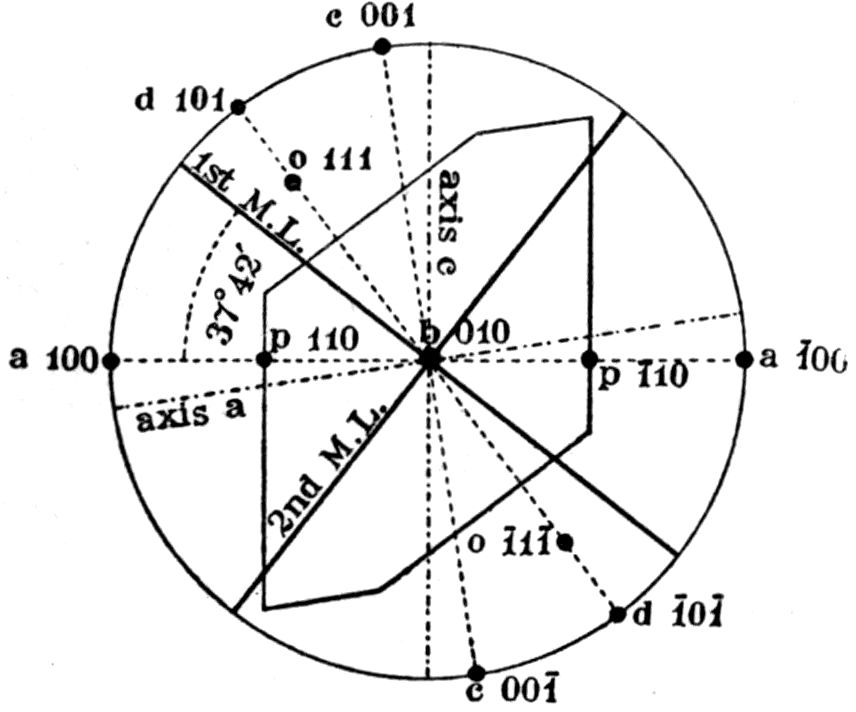
Fig. 80.—Section of Gypsum Crystal showing the Extinction Directions.
On rotating the Nicol analyser the colours change,
and appear at their
maximum brilliancy
when the field is
dark and the Nicols
crossed. Leaving
the analyser crossed
to the polariser,
and rotating the
stage and therefore
the crystal, the
colours again
change, and at
certain positions
90° apart during the rotation, marked by the two
strong lines in Fig. 80, they disappear altogether, and
the crystal becomes dark like the rest of the field,
while the positions of maximum brilliancy of colour are
found to be situated at the 45°-positions intermediate
between these positions of “extinction.” When
the quenching occurs the vibration planes of the two
rays, travelling by virtue of double refraction through
the crystal, are parallel to the planes of vibration of
the rays transmitted through the two Nicols, and the
fact is a very important one, enabling us to determine
205the directions of light vibration in the crystal. In
the case of our gypsum plate, the cleavage of gypsum
being parallel to the unique plane of symmetry of the
monoclinic crystal, these two positions are the
directions of the two axes of the optical ellipsoid
which lie in the symmetry plane, and they correspond
to the vibration directions of rays affording the
refractive indices α and γ. The direction corresponding
to γ is that of the “first median line,” the
bisectrix of the acute angle between the optic axes;
while α corresponds to the obtuse bisectrix or “second
median line.” These directions are clearly marked
by the strong lines in Fig. 80. The third axis of
the optical ellipsoid is obviously perpendicular to the
plate and to the symmetry plane, and corresponds to
the intermediate refractive index β. Thus this
simple observation of the extinction directions in
such a case as gypsum enables us at once to fix
completely the orientation of the optical ellipsoid, a
fundamental optical determination.
A second thin plate of gypsum may next be examined,
similarly prepared and mounted. It is clearly
a composite one, being composed of a pair of twins.
For when placed on the stage in the dark field of the
crossed Nicols, and rotated to the position for
maximum brilliancy of colour, it shows different
colours in the two halves, as indicated by different
shading in Fig. 81. If, however, the analysing Nicol
prism be withdrawn from the plinth-bed and removed
altogether the crystal appears in its natural colourless
condition as a single one, with no indication
whatever of any line of division.
Fig. 81.—Twin of Gypsum as seen in Parallel Polarised Light.
Some exceedingly brilliant polarisation effects
206are afforded by a number of objects exhibited by
the author in his lecture at Winnipeg, composed
of selenite (gypsum) twins and triplets, some
arranged to cross one another like the mica films
of Reusch described in the last chapter, but only
for a single rotation, three twin strips going to a
rotation, at angular distances of 120°; others are
arranged in geometrical patterns, and in circles
overlapping one another, and the whole series afford
the most gorgeous and variegated
display of colour imaginable,
the colours, moreover,
altering either on rotation
of the stage or of the analysing
Nicol, and thus passing
through every tint conceivable.
Having thus demonstrated
the usual effect afforded by a
doubly refracting crystal plate
in parallel polarised light, we may next illustrate two
special cases, which will lead us up to the case of
quartz once more. The first relates to a crystal
belonging to the cubic system, which is theoretically
singly refractive or “isotropic”; the second concerns a
plate of a uniaxial crystal cut perpendicularly to the
optic axis, the unique direction of single refraction
of such a crystal. A plate of fluorspar affords a
good example of the first case. When placed
on the stage of the polariscope it shows no colour
at all in polarised light, whatever be the position
of the two Nicols with respect to each other,
and the field remains dark when they are crossed,
207the crystal, in fact, behaving just like so much
glass.
A word of caution, however, is here necessary, for
natural mineral crystals are not infrequently
formed under conditions of considerable strain, at
high temperatures or under great pressure, as in the
case of the diamond for instance. So that we must
be careful to choose a normal and well-formed crystal
of fluorspar for our experiment. This point may be
well illustrated by placing on the stage a thick
circular plate of glass, an inch or more in diameter,
which has been purposely heated and then suddenly
cooled in order to evoke such a condition of strain.
Crossing the Nicols so as to obtain the dark field, there
is at once produced on the screen a black cross and circular
concentric spectrum-coloured rings, resembling
with wonderful simulation the interference figure,
shown in Fig. 72, Plate XIV., afforded by calcite or
other uniaxial crystal in convergent polarised light.
Artificial double refraction has been produced in the
glass by the strained conditions, in a fashion concentrically
symmetrical to the axis of the cylinder, an
interference figure being afforded symmetrical about
the axis of the cylinder as if it were an optic axis.
The diamond crystallises in the cubic system, in
octahedra, hexakis octahedra, or hexakis tetrahedra,
and should, therefore, theoretically be without effect
on polarised light. Yet it is rare to find a diamond
which does not show more or less colour in the dark
field, owing to the condition of strain in which it
exists. It is notorious that the strain is occasionally
so great that a diamond explodes into powder
shortly after removal from its enveloping matrix
208of blue clay. The author, by the great kindness of
Sir William Crookes, was enabled to show on the
screen, both in a lecture at the Royal Society and in
the Evening Discourse to the British Association
at Winnipeg, the images of ten magnificent large
diamonds, natural, perfectly formed crystals uncut
and unspoilt by the lapidary. They were mounted
between two circular glass plates of the usual 1⅞ inches
diameter, the diamonds being attached by balsam to
one of them; each plate was held in a mahogany
frame of 1⅝ inches circular aperture, the two frames
being then attached face to face to form a single one,
an enclosing cell, which could be placed on the rotating
stage as an object-slide for the projection polariscope.
The appearance of the diamonds on the screen in
ordinary light is reproduced in Fig. 82, Plate XVI.,
as well as is possible without their natural colour, for
while several of them are brilliantly colourless, others
are tinted, one being a bright green diamond. On
producing the dark field by crossing the analysing
Nicol with respect to the polariser, the darkness was
dispelled by brilliant polarisation colours, at once
revealing the diamonds and outlining them clearly
against the dark background. On rotating the
analyser the colours changed in the usual manner of
polarising objects, and bright colours were shown by
all the diamonds even when the Nicols were parallel.
It is obvious, then, that both a transparent non-crystalline
substance such as glass, and a cubic
crystal, must be free from strain in order that it shall
exhibit no colour in polarised light and, indeed, no
polarisation effects whatever, and behave as an
isotropic substance.

PLATE XVI.
Fig. 82.—Ten Diamonds exhibiting Natural Faces, mounted for the Lantern Polariscope, to show Polarisation Colours due to Internal Strain.

Fig. 121.—Doubly Refracting Liquid Crystals of Cholesteryl Acetate, projected on the Screen in the Act of Growth (see p. 281).
Two Figures illustrating the Hardest (Diamond) and the Softest (Liquid Crystals) of Crystals.
209The second special case to which attention may be
called, that of a plate of an ordinary uniaxial crystal
such as calcite, cut perpendicularly to the optic
axis, is also obviously subject to the same proviso,
that the crystal must be free from strain in order to
exhibit the normal phenomena. Such a perfectly
normal plate remains quite obscure in the dark field
in parallel light, producing neither colour nor interference
figure, even on rotation of the object stage with
the crystal, in its own plane. For the light traverses
the crystal along the optic axis, the axis of single
refraction, and the vibrations occur with equal
velocity in all directions perpendicular to it. Hence
there is no division into two rays, one retarded
behind the other on account of less velocity of
vibration, and therefore no interference colour.
And now this leads us back to quartz, for this
mineral is also uniaxial, and we will investigate in the
same manner in parallel polarised light the plates
of the mineral cut perpendicularly to the optic axis,
which have already been referred to in connection
with the experiments concerning the interference
figures produced in convergent polarised light.
Suppose we take first the large plate of quartz
7.5 mm. thick and over 2 inches in diameter.
Placing it on the stage—instead of finding the dark
field to be unaffected by the introduction of the
plate, and to remain so on rotation of the latter in
its own plane, as should theoretically be the case
if quartz were a normal uniaxial crystal, and as
calcite has been actually shown to do—we observe
that it polarises in brilliant colour, the whole hexagonal
outline of the plate, clearly focussed on the
210screen, being filled with an evenly brilliant violet
tint, the tint of passage, just as the central part of
the interference figure, within the innermost ring,
had been coloured in the convergent light experiment
with the same plate. The colour changes with
the slightest rotation of either of the Nicols, passing
into red for one direction of rotation and into blue and
green when the Nicol is rotated in the other direction.
The tint also alters when the section-plate is rotated
about its vertical diameter, by rotating the upper
adjustable part of the supporting column of the stage
within its outer fixed tubular column; this latter
change is equivalent to a thickening of the plate, the
light beam having to traverse a longer path through
the quartz during such oblique setting of the plate.
This colour is due to the same fact which produced
colour in the central part of the interference
figure, namely, the optical activity of quartz, the
fact that the plane of vibration of a beam of plane polarised
light transmitted along the axis of quartz
is rotated to the right hand or to the left. The
amount of this rotation is precisely equal, although
opposite in direction, for the two varieties of quartz,
but the rotation varies very considerably for different
rays of the spectrum. It also varies directly proportionally
to the thickness of the plate. A plate
one millimetre thick cut perpendicularly to the
axis rotates the plane of polarisation for red
hydrogen light (C of the spectrum) to the extent
of 17° 19′, for yellow D sodium light 21° 42′, and
for greenish-blue F hydrogen light 32° 46′. The
rotation is a maximum for plates perpendicular
to the axis, and the effect is inappreciable in directions
211at right angles thereto. It is clearly due to
the oppositely spiral winding of the regular-point-system
of the crystal structure, round the direction
of the optic axis, the trigonal axis of symmetry
of the crystal, a structure which we have proved
to be characteristic of quartz by the beautiful
experiments with the helical piles of mica plates,
absolutely reproducing the polarisation effects with
quartz, as described in the last chapter.
The opposite optical rotation of the two varieties
of quartz can be well shown by constructing a
“biquartz.” Two plates of equal thickness, preferably
either 7.5 mm. or 3.75 mm., are cut, one
from a right-handed and the other from a left-handed
crystal, each exactly perpendicular to
the optic axis. The two edge-surfaces to be subsequently
joined together are also cut, ground and
polished as true planes perpendicular to the plate
surfaces, and the two plates are then cemented together
with Canada balsam by these two prepared
edge-surfaces, taking care that the broad plate-surfaces
of the two halves are absolutely continuous
as if the whole were a single parallel-surfaced plate
of quartz. Such a composite plate or “biquartz,”
is one of the most useful aids to the study of optical
activity, being much used for enhancing the sensitiveness
of the determination of the angle of rotation.
When the image of such a 7.5 mm. biquartz,
mounted in the usual mahogany frame and
placed on the object stage of the projection polariscope,
is thrown on the screen—the Nicols being
crossed for production of the dark field, and the
stage and crystal plate being strictly perpendicular
212to the parallel beam of polarised light—the whole
of the screen covered by the image of the plate
appears uniformly coloured with the violet tint of
passage. But the moment the analysing Nicol
is rotated for a very few degrees, one-half turns red
and the other blue and then green. If the Nicol
be turned back again to the crossing position with
the polariser, and then rotated further in the opposite
direction to the former rotation, the appearances
on the two sides of the sharply focussed fine line of
demarcation between the two halves are inverted,
the side which formerly turned red now becoming
green, and vice versa. The two varieties of quartz
are thus oppositely affected, and it will be obvious
that the biquartz is a very delicate test for the
exact crossing of a pair of polarising prisms, or for
the determination of the mutual extinction of two
rectangularly polarised beams of light in general.
A very striking and beautiful mode of exhibiting
this opposite and equal rotation of the plane of
polarisation by the two varieties of quartz may
next be described, an experiment which we owe
to Prof. S. P. Thompson. A composite plate of
mica is constructed out of 24 sectors of 15° angle
each, the whole making up a complete circular
plate. They are cemented between two circular
glass plates of the usual 1⅞ inch size, with balsam;
the sectors are laid down in succession on one of the
plates first, side by side, with the edge of every one
in turn in close contact with the edge of the next
in order, so as to radiate from a common centre.
The second glass plate is only cemented after
the arrangement has been allowed to set for some
213days, when there is less risk of disturbing the mounting
of the sectors. The latter have all been cut from
the same film of mica, which has a thickness corresponding
to a retardation of one of the two rays
produced by the double refraction of the crystal
behind the other equal to one and a half waves.
Each sector is so cut that the line bisecting the 15°
angle is parallel to the line joining the positions of
emergence of the two optic axes of the crystal.
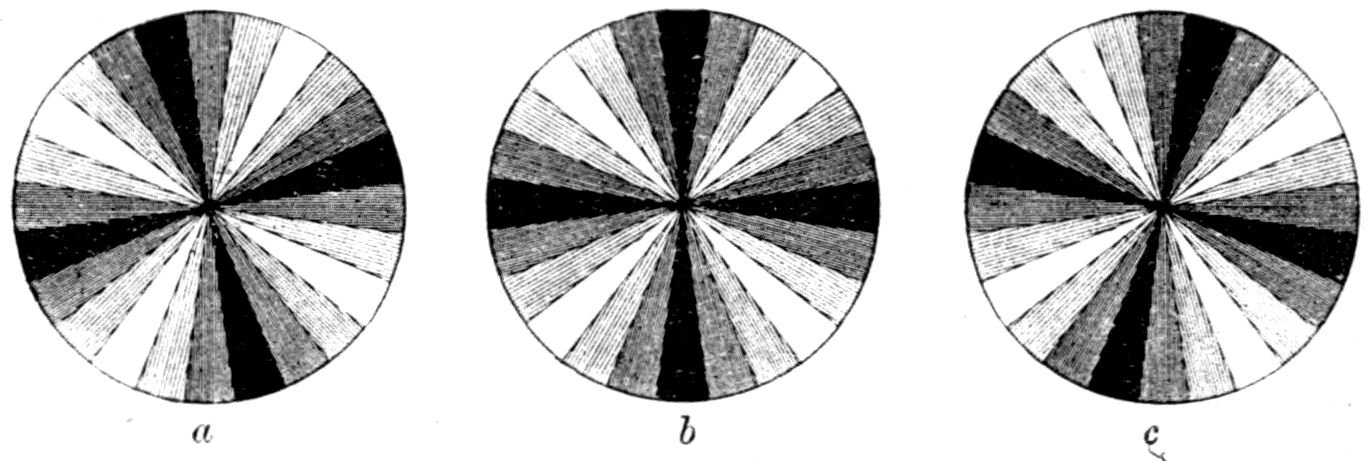
Fig. 83.—A Disc b of 24 Mica Sectors under Crossed Nicols, showing Effects at a and c of Introduction of Left and Right-handed Quartz Plates.
On placing this wheel of mica on the polariscope
stage, the Nicols being crossed, the effect shown
at b in Fig. 83 is observed on the screen. The four
sectors 90° apart, the bisecting lines of which are
vertical and horizontal respectively, parallel to the
vibration planes of the Nicols, appear as a jet black
cross; the sectors next to them appear pale brown,
and the next again a still paler delicate shade of sepia,
while the central diagonal ones of each quadrant, at
45° to the black cross, are brilliantly white.
On now introducing behind or in front of the
stage a right-handed quartz plate one millimetre
thick, one of the pair of large ones described in one
of the convergent light experiments of the last
chapter, the black cross is observed to be deflected
214one sector to the right, as shown at c in Fig. 83;
whereas when the left-handed companion plate
is introduced in like manner the cross moves over
one sector to the left, as indicated at a in Fig. 83.
The two quartz plates are mounted on the same
mahogany object frame, a specially long one with
two large apertures carrying the quartzes, so that
first one and then the other can be placed in or out
of position, and when this is done rapidly the movement
of the cross from right to left and back again
is very marked.
Occasionally a natural biquartz is obtained, on
cutting a plate out of a crystal of quartz perpendicularly
to the axis. For it is not uncommon to
find a crystal which, while apparently a single crystal,
is really a twin, the two right and left individuals
being joined by an invisible plane of contact, or
“plane of composition” as it is called, so beautifully
have the two grown together. Figs. 84 and 85
show two kinds of twins of quartz. The former
consists of two obviously different individuals,
with the little s and x faces indicating right or left-handedness clearly developed in an opposite manner.
The crystal shown in Fig. 85, however, appears to
be a single individual, yet differs from either a
right-handed or a left-handed crystal in showing the
s and x faces developed on both right and left solid
angles. It is a case of complete interpenetration.
In both cases the plane of twinning is parallel
to the optic axis, and to a pair of faces of the hexagonal
prism of the second order, perpendicular to
a pair of the actual first order prism faces shown by
the crystal. They are examples of the well-known
215“Brazilian twinning” of quartz, so called because
many quartz crystals found in Brazil display it.
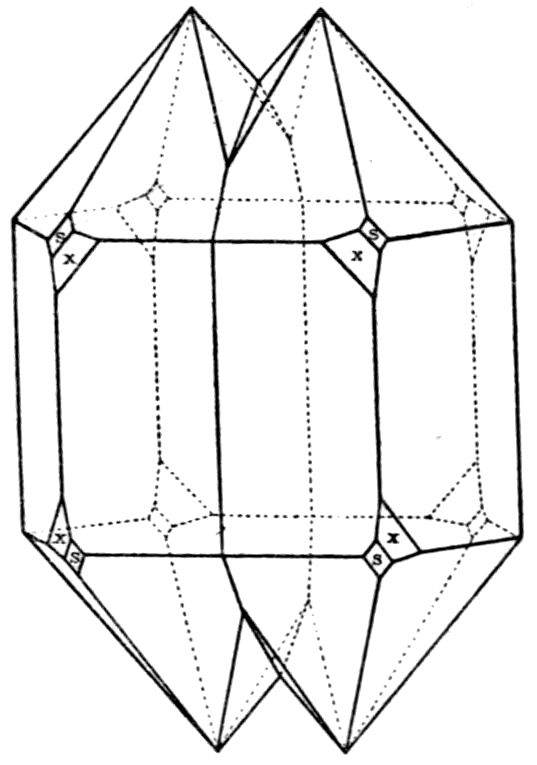
Fig. 84.—Pair of Brazilian Twins of Quartz.

Fig. 85.—Completely Interpenetrated Brazilian Twins of Quartz.
A natural biquartz of 3.75 millimetres thickness
cut from such a crystal as is shown in Fig. 85, the
plate having a hexagonal outline just as if the crystal
were really a single one, may next be projected on
the screen. The Nicols being crossed, the outline of
the crystal is seen sharply defined, the whole area of
the crystal being coloured a uniform yellow, there
being absolutely no trace of any dividing line. But
the moment one commences to turn the analysing
Nicol different shades, orange and green respectively,
begin to develop on the two sides of the line indicating
the plane of composition of the twin, the hexagon
being divided by a diametral line joining two corners,
which have been arranged in mounting the plate
in its carrier frame to be above one another, so as
to bring the line of composition vertical, as will be
216clear from Fig. 86. On rotating the analyser
further the difference is still more marked, and we
have blue on one side and orange red on the other,
developing still deeper into red and purple as the
analyser approaches the parallel position with respect
to the polariser; when this latter position is attained
the transition violet tint is developed evenly over
the whole plate, and the dividing line has again
disappeared.

Fig. 86.—A Natural Biquartz in Parallel Polarised Light.
Another natural
biquartz, also shown
in the author’s lecture
at Winnipeg, introduces
us to a new
phenomenon. For
when the Nicols are
crossed we observe a
black band down the
centre of the plate,
marking the line of
division of the twins.
When the analyser
is rotated until it is parallel to the polariser
this black band changes to a white one, the
sequence of colours on the different sides of the
band, that is, in each half of the plate, being
the same as just described. The effect with crossed
Nicols is more or less simulated in Fig. 87, Plate
XVII., which is a reproduction of a direct photograph
of the screen picture. The reason for this
black band in the dark field, and for the white one
in the bright field, is that the two halves of the twin
overlap at the centre, the plane of junction of the two
individual crystals being oblique to the plate, instead
of exactly perpendicular thereto as was the case with
the first natural biquartz. We are, in fact, beginning
to get the effect of two superposed wedges of quartz.

PLATE XVII.
Fig. 87.—Natural Biquartz exhibiting the Black Band (Nicols crossed) at the Oblique Junction of the Right-handed and Left-handed Parts.

Fig. 88.—Artificial Biquartz, the two parts being obliquely joined in order to produce the Black Band.
Direct Photographs of Pictures projected on the Screen by the Lantern Polariscope, using Parallel Light.
217When the obliquity is greater, or the crystal
thicker, a white band appears on each side of the
black central one, the Nicols being crossed, and
when the thickness is as great as 6 to 7.5 mm. a
spectrum band appears on each side of the white one.
That this obliquity of the surface of contact of
the two intergrown individuals (not the plane of
twinning, which remains parallel to a pair of faces
of the hexagonal prism of the second order) is the
true explanation can be readily proved by reproducing
the effect artificially. A thick double plate
of quartz is constructed, as shown in Fig. 88, composed
of two halves of respectively right-handed
and left-handed quartz, each 6 to 7 millimetres
thick, and each of which has had the edge-face of
junction ground and polished obliquely at an angle
of 30° or so, and oppositely so, instead of perpendicularly
to the plates; the two halves are then cemented
together in the usual manner for a biquartz, with
Canada balsam, in order to make a continuous
plate. On placing the plate of this construction
possessed by the author on the stage of the projection
polariscope, the two halves exhibit on the
screen respectively brilliant red and green colour,
with a vertical central black band, and on each side
of it first a white strip and then a spectrum band,
all the bands being parallel to each other, and
the whole effect being precisely what was observed
with the thickest natural biquartz.
218Thus, we have imitated the oblique junction of
the twin parts of the second and third biquartzes,
and proved that this obliquity is the reason for the
phenomena of bands, the black band occupying
the centre where the two opposite rotations of the
right and left quartz are precisely neutralised. The
dark field of the crossed Nicols consequently prevails
along this central strip, for the rotatory effect
of the first individual crystal on the light passing
through it is exactly undone by the subsequent
passage of the rays through the other individual.
On either side of this neutral strip there is a little
preponderance of right-handed quartz on one side,
and of left-handed quartz on the other, and the
usual effect of a thin plate of quartz is therefore
seen, namely, no colour but a little light, while
further accretions of thickness of the preponderating
variety give all the colours of the spectrum in turn,
as with growing thicknesses of ordinary single
quartz plates, thus producing the spectrum band.
The black band is also afforded when the plate is
cut somewhat obliquely, out of a twin crystal with a
junction plane truly perpendicular to the equatorial
section, instead of cutting it truly perpendicularly to
the axis, the junction plane being then oblique to
the plate. The polarisation colours are not so strong,
however, unless the plate be made thicker.

PLATE XVIII.
Fig. 89.—Black Central Band and equidistant Spectrum Bands on each side, afforded by Babinet’s Composite Plate of two Quartz Wedges, one parallel and the other perpendicular to the Axis. (Direct Photograph of Screen Picture as projected by Lantern Polariscope.)
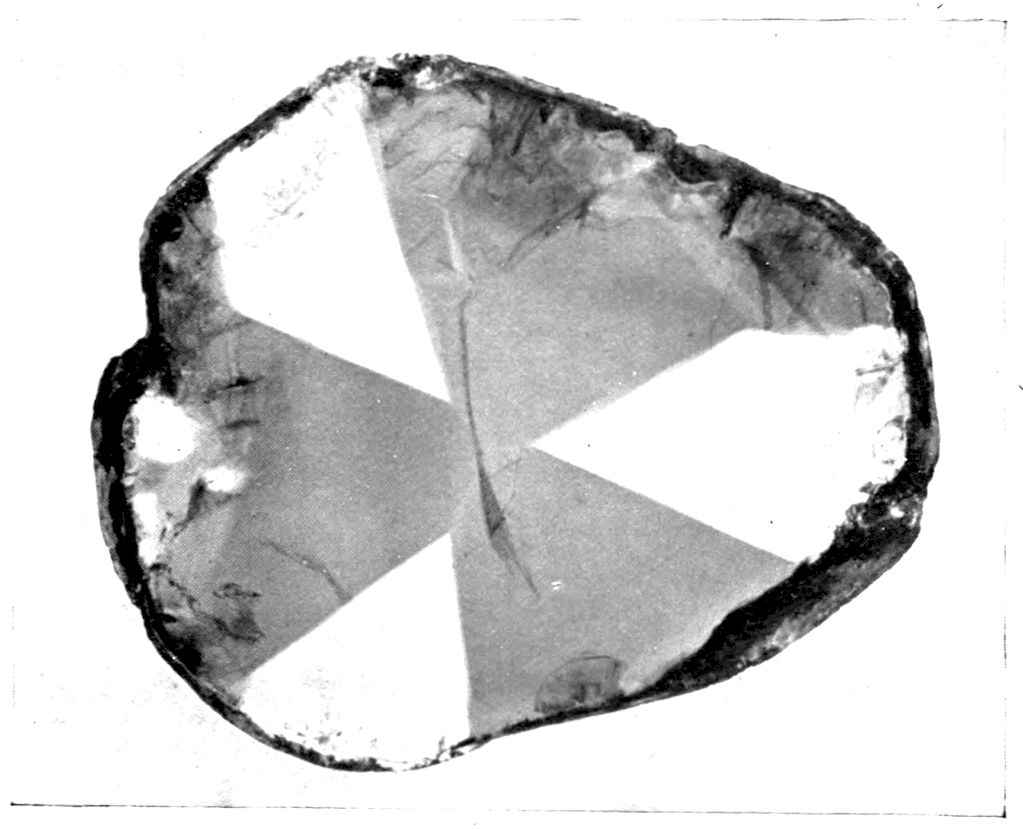
Fig. 94.—Section-plate of Amethyst, natural size, as seen directly in Ordinary Light, showing Alternate Violet Sectors (see p. 223).
219This effect of a black band with flanking spectra
is very similar to that obtained, due to double
refraction and not to optical activity, when two
thin wedges of quartz are cemented together to
form a parallel plate, one wedge being cut so that
the optic axis is parallel to the edge of the wedge,
and the other with the optic axis perpendicular
to the edge. When such a composite plate of quartz,
often known as a Babinet plate from the name
of its first constructor, is placed on the stage of
the polariscope, and rotated to the 45° position
with respect to the planes of vibration of the
crossed Nicols, there is observed on the screen a
deep black band in the centre parallel to the edge
of the wedge, and a number of spectrum bands on
each side, separated by white equal interspaces,
the rainbow coloured bands showing the orders
of Newton’s spectra. The effect, as seen on the
screen, is reproduced photographically in black and
white in Fig. 89, Plate XVIII.
These experiments lead us naturally to the study
of a great variety of quartz twins, involving some
of the most beautiful and gorgeously chromatic
phenomena which it is possible to produce on the
screen with the projection polariscope. They will
eventually bring us to the study of amethyst quartz,
in which the twinning is repeated so often that the
laminations of alternate right and left quartz are
sometimes countless, and almost approach molecular
dimensions.
The Brazilian twinning of quartz, parallel to a
pair of faces of the second order hexagonal prism
{11̄20}, often occurs in a very erratic manner, as
regards the arrangement of the portions of the composite
crystal belonging to the two varieties, the surfaces
of contact and character of the interpenetration
being frequently very irregular, and often remarkably
so. Thus Fig. 90, the upper figure of the coloured
frontispiece, gives some faint idea of the appearance
220presented on the screen by a very beautiful quartz
plate, one-half of which is entirely composed of left-handed
quartz, giving a rich even rose-red colour
when the Nicols are crossed, not very far from the
violet transition tint, the plate being nearly 7.5 mm.
thick, while the other half consists of an alternation of
strips of right and left-handed quartz, joined obliquely
to the surface of the plate, the black band and its
accompanying white ones and spectrum bands being
repeated two or three times before the edge is reached.
This is a very instructive case, for it shows in this
half of the plate, on a large scale, what occurs in
amethyst in a more minutely structural manner,
the broad strips, the sections of plates upwards of
a quarter of an inch thick, of alternating character
becoming in amethyst thin lines, the sections of
laminæ or films of microscopic tenuity, their number
being correspondingly enormously increased.
It may be interesting to state how this Fig. 90, and
the lower Fig. 97 of the frontispiece representing the
projection on the screen of benzoic acid in the act of
crystallisation, were produced. The pictures on the
screen were directly photographed on the latest
Lumière autochrome plates, a transparency in the
actual natural colours being thus obtained in each
case. These transparent colour-photographs were
then used as originals wherewith to reproduce the
effects on paper by the most recent improved three-colour
photographic process.

PLATE XIX.
Fig. 91.—Sectorial 60° or 120° Intrusive Twinning of Right and Left-handed Quartz, showing Ribbons with Central Black Band where Oblique Overlapping occurs.
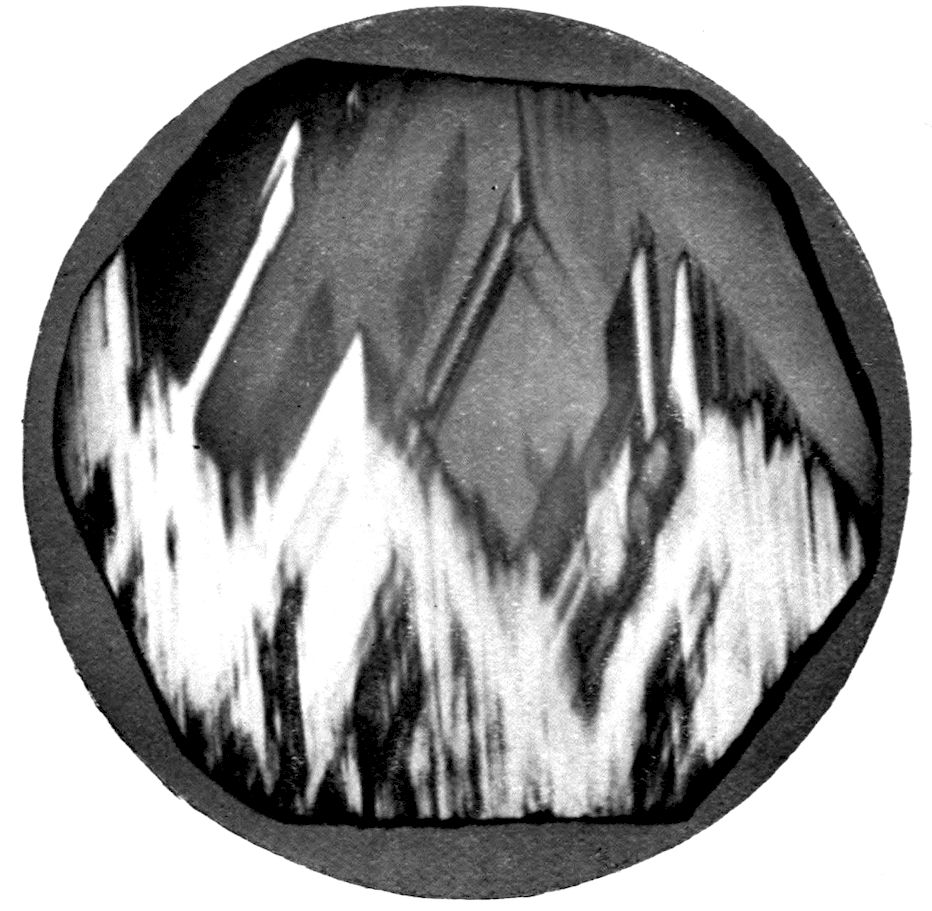
Fig. 92.—Irregular Intrusive Twinning of Right and Left-handed Quartz.
Direct Photographs of Remarkable Screen Pictures afforded in Parallel Polarised Light by Sections of Twins of Right and Left Quartz.
221Two other typical cases of irregular quartz twinning
may also with advantage be demonstrated. The
first is a plate in which there are repeated 60°
V-shaped or 120° wedge-shaped intrusions of one
variety into a greater mass of the other variety.
The border of the V or 120° wedge is composed
of a ribbon, the outer edges of which are spectrum-coloured
and the central line of which is formed by
the deep black band, which is separated on each
side from the spectra by a white strip. Some idea
of the beauty of this quartz plate, which was
generously lent to the author by Prof. S. P.
Thompson, as projected on the screen under crossed
Nicols, may be gathered from Fig. 91, Plate XIX.,
the upper homogeneous part of the plate being
coloured a brilliant green, and the lower part red.
The second is an irregular interpenetration of
one variety into the other, in repeated V-shapes
occupying the lower half of the image of the plate
as seen on the screen in the dark field of the projection
polariscope, like a range of sharp mountain peaks,
the black bands being so rapidly repeated as to be
nearly continuous. These darker portions thus
appear to form the bulk of the mountains, while the
upper untwinned half of the crystal shows a clear
and even sky blue; to make the resemblance to a
range of Alpine mountains even more complete,
the wavy line of demarcation between the twinned
and non-twinned portions of the plate is bordered
by a white ribbon, of varying width, giving the
appearance of a snow-cap to each peak, which shows
up clearly against the blue sky. It will be obvious that
this quartz plate affords an altogether very beautiful
series of phenomena in parallel polarised light on the
screen, for the colours change with every movement
of the analysing Nicol from the crossed position,
the appearance for which has just been described.
222Fig. 92, Plate XIX., gives only the faintest idea
of the beauty of the screen picture afforded by this
section-plate. The effect chosen as best for photographic
reproduction purposes is one afforded when
the analysing Nicol is rotated somewhat away from
the crossed position with respect to the polariser.
And now we arrive finally at amethyst quartz,
three very beautiful hexagonal plates of which—cut
perpendicularly to the optic axis as usual for
quartzes intended to display optical activity, from
an apparently single hexagonal prism in each case—will
be taken as typifying the phenomena exhibited
by this especially interesting variety of quartz on
the screen in parallel polarised light. The smaller
one affords a screen picture, with Nicols not quite
crossed, such as is portrayed in Fig. 93, Plate XX.
We observe that the area of the hexagon is roughly
divisible into six 60°-sectors, and that alternate ones
are uniformly coloured, indicating that they belong to
wholly right-handed or left-handed quartz; whereas
the other alternate sectors are most beautifully marked,
as if by line shading parallel or inclined at 30° to the
edges of the hexagon, by a considerable number of
equally spaced dark or slate coloured bands, close
together but separated by white bands, with a trace
of spectrum colours along the middle of the latter.
If we rotate the analysing Nicol somewhat we can
readily find a position, which is not always that
of crossed Nicols, for which these parallel bands of
laminar twinning are most clearly defined, as shown
in the illustration, the colours of the other sectors
ever changing during the rotation.

PLATE XX.
Fig. 93.—Section-plate of Amethyst Quartz, showing Sectorial Repeated Twinning of the Right and Left Varieties.
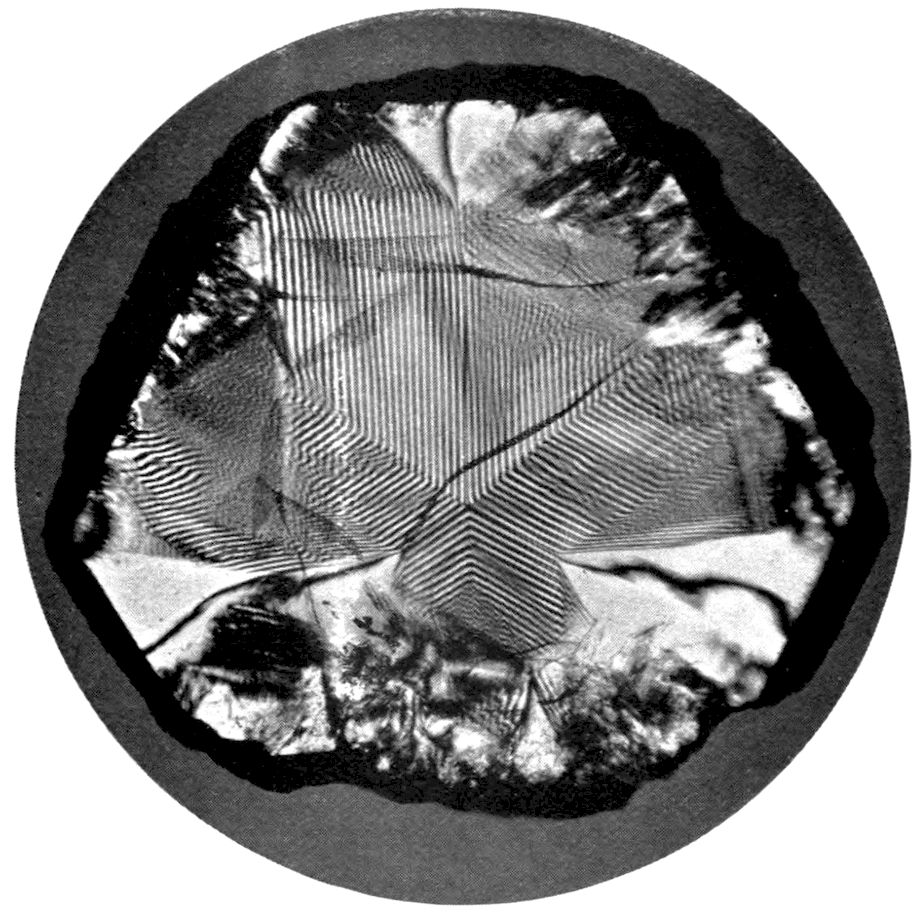
Fig. 95.—Section-plate of large Amethyst Quartz Crystal, showing relatively large Area of Sectorial Repeated Twinning of Right and Left-handed Quartz (see p. 225).
Direct Photographs of Screen Pictures of Amethyst projected by the Lantern Polariscope in Parallel Light.
223It is obvious that we have here to do with the
same phenomenon as was illustrated by the parallel
bands shown on the large scale by the section
illustrated in Fig. 90 of the coloured frontispiece,
the black, white, and spectrum-coloured bands being
simply repeated very many more times in the same
space, and in alternate sectors of the crystal.
The twinning of amethyst in 60°-sectors is very
characteristic of this variety of quartz, and it is
an interesting fact that the sectors which show the
laminar bands in polarised light often appear
purple coloured in ordinary light, the tint from
which amethyst derives its name. This is not
necessarily or always so however, and the section
just described and illustrated in Fig. 93 appears
quite colourless throughout on casual inspection
in ordinary light, in fact as a clear colourless hexagonal
section of ordinary simple quartz; a trace of
the amethyst colour becomes, however, apparent on
closer examination when held obliquely, in the sectors
where the bands become visible in polarised light.
The second plate of amethyst is a magnificent
section 9 millimetres thick and 2½ inches in
diameter, of which alternate 60°-sectors are deeply
amethyst coloured, the tint being a pure violet
of about the wave-length of the hydrogen line near
G of the spectrum. Moreover, even to the naked
eye when the specimen is held in the hand up to
the light, in certain positions the laminæ become
visible as more deeply shaded violet line markings.
On placing it on the stage of the polariscope but
with the analysing Nicol removed, so as to observe
the natural appearance of the section in white light
(for, although polarised by the polarising Nicol, being
224unanalysed the section exhibits no polarisation effects),
these facts become clear to everyone in the room.
The violet staining of alternate sectors appears
very deep, and traces of lamination in the violet
parts are just apparent on close scrutiny, the other
alternate sectors appearing colourless and unmarked
except by a few flaws almost always present in so large
a section-plate of amethyst. The natural appearance
of this plate is shown in Fig. 94, Plate XVIII.
(facing page 218), as far as is possible photographically,
the violet sectors being clearly demarcated.
On replacing the analysing Nicol the colourless
sectors are seen to polarise uniformly in brilliant
colours, indicating a homogeneous variety of quartz
in each, either right or left-handed. Moreover,
whenever two of these naturally colourless parts
touch each other, which they do as the margin of
the plate is approached, an irregular ribbon is produced,
composed of the black band in the centre,
with first white and then spectrum-coloured flanking
strips on each side, the spectra forming the edges
of the ribbon. The violet sectors show the laminated
twinning, but, owing to the great thickness of this
plate, in too complicated (overlapping) a manner
to be easily followed, a thinner plate being required
to show such fine laminations clearly.
Finally, the third section is such a thinner plate,
about 3.5 mm. thick and nearly 1½ inches in diameter.
This section of amethyst is probably the most
beautiful of all, for it not only shows the laminated
twinning to perfection, in three alternate 60°-sectors
and in all six in the middle part of the plate,
but also these alternate sectors are distinctly
225violet even to the eye when the specimen is held
in the hand against a white background; and the
laminations are likewise also clearly visible on
holding the section obliquely up to the light. In
polarised light, either with crossed or parallel or
anyway arranged Nicols, the phenomena on the
screen are of the most superb character. The
whole of the middle part of the plate appears made
up of six sectors, all showing the fine laminar bands
parallel to the edges of the second order hexagonal
prism {11̄20}, that is, at 30° to the edges of the
section, the crystal being a first order hexagonal
prism {10̄10}. Some idea of the arrangement will
be afforded by Fig. 95, Plate XX. The marginal parts
develop into alternately right and left-handed sectors
or half-sectors, polarising in different and very
brilliant colours, and showing the ribbon bands at
every junction. On rotating the analysing Nicol the
changes are remarkably beautiful, particularly for
the positions of the analyser when the laminar
bands take on their deep slate colour, with white
and marginally spectral interstrips. The whole
phenomena, indeed, afforded by this plate of amethystine
quartz, are the most magnificent which the
author has ever seen on the screen, in the whole of
his crystallographic experiences.
The Brazilian twinning law of quartz, according
to which the plane of twinning is parallel to a pair
of faces of the second order hexagonal prism {11̄20},
appears capable of explaining all these varieties of
right and left-handed twins, the interpenetration of
the intimate kind shown in Fig. 85 (page 215) usually
resulting in sectorial portions of space being occupied
226by each kind, the surfaces of junction of oppositely
optically active parts being, however, very varied
in their distribution and character. Where they
happen to be more or less horizontal, a plate cut
perpendicularly to the axis to include both kinds
would show Airy’s spirals in convergent polarised
light, as may readily be demonstrated by such a
plate, one of several, in the author’s collection.
Where they are oblique, a plate cut at right angles
to the axis would, as we have seen experimentally,
afford the black, white and spectral ribbon bands
in parallel polarised light. Where, however, the
mode of interpenetration is still more intimate,
we have the rapidly alternating laminæ of the
two varieties, right and left-handed, building up
the beautiful structure of amethyst in thin layers.
A section-plate of such an intimate blending of the
two varieties, cut as usual perpendicular to the
axis in order that any phenomena of optical activity
shall be exhibited at the maximum, affords no
indication whatever of optical rotation, the two
varieties simply neutralising each other’s effects,
and the plate behaves as an ordinary uniaxial
crystal, affording in convergent polarised light a
black cross like calcite, complete to the centre.
In parallel polarised light it shows of course the
laminated structure, but the tendency to remain
dark under crossed Nicols is shown by the fact
that the tints exhibited by the laminations are
slates, greys, and even black, when the Nicols are
crossed, the delightful other colours only making
their appearance when the analysing Nicol is rotated.
Thus the simple law of Brazilian twinning is quite
227capable of explaining the whole of the phenomena
exhibited by composite crystals of the two varieties
of quartz, and such an explanation is the one accepted
by von Groth, in the excellent description of quartz
in the last edition of his Physikalische Krystallographie.
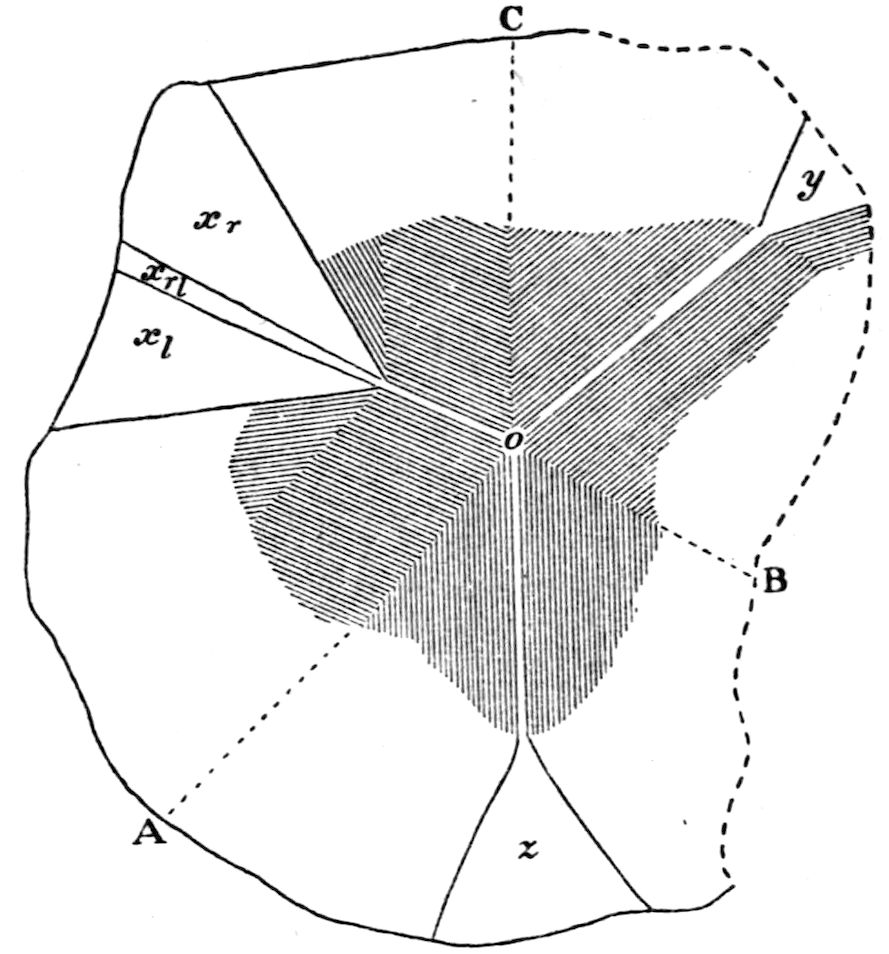
Fig. 96.—Plan of Amethyst Crystal.
An interesting crystal of amethyst very similar
to the third of those just described, the one illustrated
in Fig. 95, was described by Prof. Judd
in the year 1892 to the Mineralogical Society.[18]
The plan of the crystal is given in Fig. 96. The
wedges marked x, y, z, are of a pale yellow colour,
as are also the three strips, sections of plates, proceeding
from the wedges and meeting at the centre
228o. The wedge y exhibits left-handed polarisation,
and the wedge z right-handed. The large wedge
x is composite, the part marked xr being right-handed
and that marked xl left-handed. The surface
of junction of the two parts is not perpendicular
to the plate, so where the two varieties overlap,
the part marked xrl, a ribbon band is shown in
parallel light and Airy’s spirals in convergent polarised
light. The yellow parts of the crystal exhibit
ordinary rotatory polarisation colours, even tints;
but in the remaining sectors of the crystal, the lines
of division of which are indicated by the radial
lines A, B, C, no trace of circular polarisation is
displayed, and the central part, where the lamellæ
are very well developed, gives the ordinary calcite-like
uniaxial interference figure. The more marginal
portions, however, show complicated interference
figures, somewhat resembling those of biaxial
crystals, owing to irregular distribution of the two
varieties of quartz, and probable displacement
of the optic axis by distortion.
An ingenious theory of the formation of the
lamellæ is put forward by Prof. Judd in the same
memoir. He had already shown that quartz is
endowed with planes of gliding, parallel to the
rhombohedral faces, and suggests that the lamellation
is the result of the effect of high pressure and
possibly high temperature on the quartz crystal
after its formation. The lamellæ appear to be
frequently parallel to the rhombohedral terminal
faces of the crystal, as if they were indeed glide
plane effects. It is quite conceivable that the
gliding of layers of molecules, which when permanent
229usually involves rotation and inversion of
the molecules, might result in alternately right
and left structural arrangements, and there is considerable
evidence that the development of the
purple tint occurred subsequently to the growth
of the crystal. It is probably due to change in
the state of oxidation of the trace of manganese
present as a minute impurity in the quartz crystal,
and which is concentrated between the lamellæ,
just as the yellow tint is due to a slight trace of
iron (ferric) oxide. The theory is an interesting
one, and throws considerable light on the possible
nature of intimate lamellar twinning.
One last experiment may now be referred to,
the concluding experiment of the Winnipeg lecture,
and which is very reminiscent of the beautiful
slate colour of the lamellæ of amethyst. It is the
actual crystallisation, projected on the screen, of
a thin film of melted benzoic acid, which affords
radiating closely packed long and narrow crystals,
shooting out on the screen from centres near the
margin of the field, very much like the individual
crystals of repeatedly twinned quartz in the beautiful
amethyst crystal illustrated in Fig. 95. Provided
the film of melted benzoic acid be thin enough, the
crystals appear on the screen in parallel polarised
light, under crossed Nicols, tinted with the same
beautiful shades of slate colour as amethyst, the
intermediate low-order tint between the black and
the grey of Newton’s first order spectrum. Some
idea of the appearance on the screen is afforded
by Fig. 97, the lower of the two coloured figures in
the frontispiece. As in the case of Fig. 90, the
230screen picture was photographed directly on a
Lumière autochrome plate, and the transparency in
the actual colours thus obtained was employed as an
original wherewith to reproduce the picture on paper
by the latest three-colour photographic process.
In carrying out the experiment a few of the flaky
crystals of benzoic acid are placed on one of the
circular glass object plates of the standard 1⅞-inch
size for the projection polariscope; they are covered
by a second similar one, and the two plates are then
held in a pair of tongs and gently warmed over a
small spirit lamp, or miniature Bunsen lamp. As soon
as the crystals have fused, and the melted substance is
evenly spread as a thin film between the two glass
plates, the latter are rapidly transferred to a special
mahogany object frame, fitted with a side slide to
press the double-plate edge just sufficiently to hold
it in position in the frame, which is then at once
placed on the rotating stage of the polariscope. The
screen appears quite dark at first, the Nicols being
crossed, but in a second or two as the slide cools
the benzoic acid begins to crystallise out at the
sides, brilliant colours and the deep greys being
both developed, the former chiefly near the edges of
the crystals, rendering the crystallisation wonderfully
distinct and beautiful on the black background.
Then long needle crystals shoot out from various
quarters one after another or simultaneously, in
lovely shades of slate or grey tinted with brilliant
colours at the margins and tips, the growing point
cutting its way along like a sharp brilliantly coloured
arrowhead. Eventually an arch is formed of such
acicular crystals, radiating simultaneously from
231many centres, gorgeously coloured in parts, but
showing the yet more æsthetic slates and greys in
the main. Finally, the whole screen picture fills
up with a mass of interlacing yet ever distinct
crystals, the last few to crystallise in the centre
usually doing so with a burst of especially bright
colour, as the thickness increases adequately for
the double refraction retardation to reach the
more brilliant second order spectrum, a concluding
effect which evokes the emphatic delight of even the
most phlegmatic philosopher, inured to scenes of
beauty in natural phenomena.
The series of experiments with quartz described
in this and the previous chapter, culminating with
those revealing the alternate repetition of extremely
fine layers of right and left-handed quartz in
amethyst, will, it is hoped, have illustrated and
rendered intelligible the important structural
principle of enantiomorphism or mirror-image
symmetry. We have only to imagine the layers
to become thinner and thinner until we approach
ultimately the neighbourhood of the minute dimensions
of the chemical molecule, without as yet
penetrating within the range of the molecular
forces; the two such oppositely constructed and
intimately blended structures, built up by atoms
arranged oppositely screw-wise, clockwise and anti-clockwise,
will now form an ultramicroscopic mixture
of the two varieties in equal quantities, that is, in
equal molecular proportions.
Such a structure will exhibit the symmetry of
the system to which the two individuals belong,
but instead of only displaying that of the enantiomorphous
232class of that system, possessing lower than
the full symmetry, as each variety does when
crystallised alone, it will now display the full holohedral
symmetry of the system. That is, the
symmetry is enhanced by this intimate blending
of the two complementary enantiomorphous forms,
the two together supplying all the possible elements
of symmetry of which the system is capable. Moreover,
as we have seen in the case of the lamellar
portion of the amethyst crystals represented in
Figs. 95 and 96, there will now be no sign of optical
activity, for the two opposite rotations are equal
and destroy each other.
Hence, such a compound crystal shows the
holohedral symmetry of the system, and is optically
inactive. In such cases we are, in fact, confronted
with the phenomenon of pseudo-racemism, as
defined in Chapter XI. For we know that the
two varieties are still present intact, polarised light
revealing them in the case of their grosser development
such as is found in amethyst, and the system of
symmetry being clearly the same, the forms developed
being merely the sum of those of the two
individual varieties.
Amethyst thus affords us a gross demonstration
of the nature of pseudo-racemism, and as such has
proved an exceedingly illuminating study.
We can carry the process further, however, in
imagination, until the two differently helical molecules
are themselves juxtaposed face to face, right
molecule to left molecule. When, however, this
occurs, we have entered into that most fascinatingly
interesting region, the range of molecular forces,
233a mysterious sphere of activities of which we are
only just beginning to learn something. Within
this region of larger activity the two oppositely constructed
molecules are often known to combine
chemically to produce a molecular compound,
just as potassium sulphate molecules, for instance,
will combine with those of magnesium sulphate
to form the well-known double salt. The double
molecule now furnishes the representative point of
the space-lattice, in other words, a new space-lattice
is now erected, the units of which may be
taken to be the representative points of the double
molecules. Such a space-lattice will of necessity
be of a totally different character to the old one
corresponding to the single molecule of either
variety (for each variety has the same space-lattice,
the points, however, representing differently,
enantiomorphously, orientated atomic details).
That is to say, we shall have an entirely new kind of
crystal produced, in all probability belonging to
a different crystal system. It is known as a racemic
compound, as described in Chapter XI.
This is exactly what happens in the case of tartaric
acid, the two varieties, dextro or right-handed
tartaric acid and lævo or left-handed tartaric acid,
not forming pseudo-racemic crystals of like but
enhanced (holohedral) symmetry, but a truly molecular
compound, the well-known inactive racemic
acid, in which the phenomenon of “racemism” was
first discovered and from which it took its name.
Now a molecular compound is notoriously regarded
by chemists as a type of chemical compound of
low stability, molecular attraction or affinity not
234being nearly so powerful as atomic affinity. Hence,
under suitable conditions it may be possible to
induce the two component varieties to crystallise
out separately from the solution of the racemic
compound. In the case of racemic acid itself this
does not readily happen, but in the cases of certain
of its metallic salts, sodium ammonium racemate,
for instance, specific conditions are known under
which the two varieties of crystals, right and left-handed respectively, may be separately crystallised
out from the solution, some of which conditions
were referred to in Chapter XI. Racemic acid
itself, however, crystallises quite differently to
the two tartaric acids, namely, in triclinic prismatic
crystals. These are, in fact, absolutely different from
the monoclinic crystals of the dextro and lævo
varieties of ordinary tartaric acid, for racemic acid
takes up also a molecule of water of crystallisation
on separating from its aqueous solution. There are
certain chemical differences also, due to the chemical
union of the two enantiomorphous molecules into a
single double molecule, such, for instance, as greater
facility of reduction by hydriodic acid to succinic
acid.
Thus our experiments with quartz have afforded
us the means of acquiring a clear idea of the nature
of this most interesting type of crystal structure
which involves the principle of mirror-image
symmetry. Racemic acid and its similar structures,
racemic compounds in general, are known as “externally
compensated” structures, the reflective
principle here acting externally to the single enantiomorphous
molecule. It is but another step, however,
235to imagine internal compensation of enantiomorphous
parts of a molecule, by mirror-image
combination of such parts, such as in all probability
occurs in the case of the truly inactive fourth variety
of tartaric acid, in order to comprehend how the
principle enabled the 165 types of homogeneous
structure involving this kind of repetition to be
arrived at, and thus, together with the 65 regular
point-systems already known, to afford us the
complete set of 230 types of homogeneous structures
possible to crystals.
236
CHAPTER XV
HOW A CRYSTAL GROWS FROM A SOLUTION.
One of the most deeply interesting aspects of a
crystal, especially from the point of view of the
history of crystallographic investigation, concerns the
mysterious process of its growth from a solution
(in a solvent) of the substance composing it. The
story of the elucidation, as far as it has yet been
accomplished, of the nature of crystallisation from
solution in water is one of the most romantic which
the whole of scientific progress can furnish. Again
we are struck with the parallelism between crystals
and living objects. For just as the discovery of
bacteria, the infinitesimal germs of life, has given
an immense impetus to our knowledge of disease
and been blessed with most beneficent effects in
combatting the ravages of the latter, so the discovery
that crystal-germs of most common crystallised
substances, of no larger size than bacteria,
are floating about in our atmosphere, and ready at
any time to drop into our solutions and, if the
latter are in the proper receptive condition, to set
them crystallising, is little less marvellous, and has
had as profound an effect on our knowledge of the
process of crystallisation. A true story, told to the
Royal Society the other day, may serve to illustrate
the point. A new chemical compound had been
237discovered, and at the time there could obviously
be no crystal-germs, minute crystallites of the
dimensions of possibly only a comparatively few
chemical molecules, of this hitherto unknown
substance floating about in the air. It was found
impossible to obtain the deposition of crystals in
the ordinary way, from solutions of the substance
in its ordinary solvent, although they were in the
condition of proper receptivity above referred to,
on account of the absence of such germs in the air.
But later on, when the air of the laboratory had
become impregnated with such germs, on account of
the daily handling of the substance in the laboratory,
no difficulty was any longer found in
obtaining good crystals quite readily from these
solutions.
We are at first inclined to wonder whether such
extraordinary statements can possibly be sober facts.
Yet such is, indeed, the case, and it will be very
well worth devoting a chapter to the story of how we
have at length arrived at definite knowledge concerning
the process of crystallisation from the state of
solution in water. For water is the ordinary solvent
from which we obtain our crystals, that is, such as
are prepared artificially in the laboratory. The laws
which have been discovered to hold for aqueous
solutions are, however, equally applicable to the
cases where other solvents are used, such for instance
as the usual organic solvents like alcohol, ether,
chloroform, and benzene.
The conditions under which crystallisation occurs
from the liquid state, or from solution of the substance
in a solvent, have been accurately determined
238experimentally by H. A. Miers,[19] and they bear out
in the main the predictions from theoretical considerations
which were made by Ostwald.[20] Taking
first the case of crystallisation from solution, there
are two distinct curves representing the degree of
solubility of the solid substance and of supersolubility.
The well-known ordinary solubility
curve is obtained by taking the temperature for
abscissæ and concentration for ordinates, so that
any point on the curve indicates the amount of
the solid substance which the solvent can hold in
solution at that particular temperature. Now the
fact that supersaturation may occur has long been
established, the phenomenon being of frequent occurrence;
and it is common knowledge that a supersaturated
solution may be preserved for a long time
without crystals being deposited from it, provided
the liquid be maintained quietly at rest. Obviously,
therefore, this condition of supersaturation ought
to be represented by a second curve a few
degrees lower as regards temperature than the
solubility curve, and its conditions were fairly
fully predicted by Ostwald, after collecting together
and analysing the results of the experiments
of Gernez, Lecoq de Boisbaudran, J. M.
Thomson, de Coppet, Lefebvre, and Roozeboom.
It was reserved for Miers, however, to discover
a means of experimentally tracing this curve, by
observations of the refractive index of the solution.
The point at which the deposition of crystals from
239the supersaturated solution occurs is immediately
indicated by a sudden change in the refraction of
the liquid, the refractive index attaining its maximum
value at the temperature of spontaneous
crystallisation, and then dropping suddenly the
moment the crystals begin to fall. Moreover, the
solution at the same time records its own strength,
for the refractive index varies directly as the amount
of salt dissolved. The determination of the strength
of the solution at the critical moment itself had
previously proved an impossibility by ordinary
methods.
Fig. 98 gives a general diagrammatic representation
of Miers’ results for a typical crystalline
substance soluble in water. S is the ordinary
solubility curve, which may also be termed the
“curve of crystallisation by inoculation.” For
as soon as the solution reaches this condition of
normal saturation it is liable to be caused to
commence crystallising if a germ crystal, that is,
a miniature crystallite floating in the air as dust,
of the substance itself or of one isomorphous with
it or capable of forming parallel growths with it,
fall into the solution from the air. It has been a
revelation to us that such minute crystallites of
all common substances are scattered broadcast in
our atmosphere, and that sooner or later one will
introduce itself into any solution set to crystallise
which is not sealed up or placed in a vessel with a
filtering plug of cotton-wool in its neck or other
aperture.
240
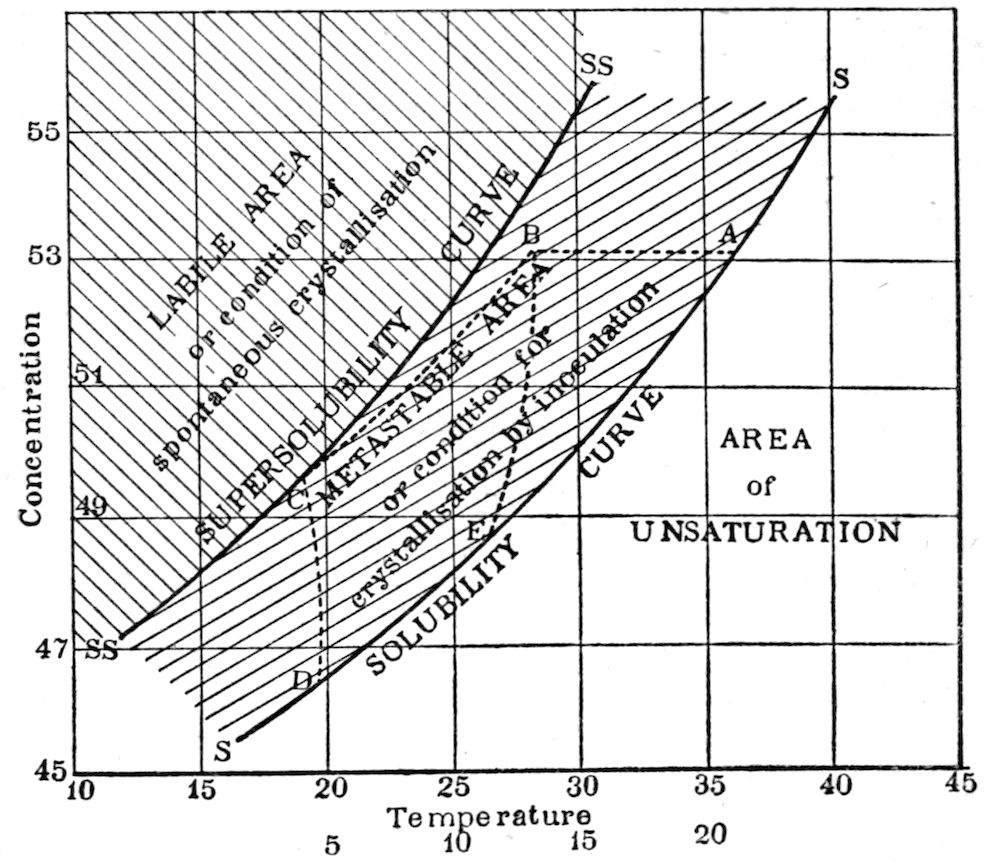
Fig. 98.—Diagram illustrating the Conditions for Crystallisation from Solution or the Liquid State.
SS is the supersolubility curve, situated approximately
10° to the left of the solubility curve as
regards temperature, but about as much above
as regards concentration, so that the two curves
usually run diagonally and more or less parallel
to each other across the diagram. This supersolubility
curve may be also called the “curve of
spontaneous crystallisation,” for it represents the
conditions under which alone crystals may begin
to form without the initiating impulse of inoculation
by a germ-crystallite. On the suggestion of Ostwald
it is also termed the “metastable limit,” and the
whole area between the solubility and supersolubility
curves is named the area of metastability,
that which represents the “metastable” condition
of the solution. Within this area the conditions
241are those for the start of crystallisation by inoculation.
The area beyond the supersolubility curve
represents the “labile” state, in which the conditions
are those for spontaneous crystallisation,
inoculation being no longer necessary. These
precise results will, it is hoped, be quite clear with
the aid of Fig. 98.
Hence, when a cooling solution not quite saturated
at the higher starting temperature is stirred
in an open vessel a slight shower of crystals, started
by inoculation, appears when the saturation point
is reached, which Miers calls a “metastable shower,”
corresponding to the ordinary solubility curve;
the liquid then goes on cooling without depositing
the main bulk of the excess which that curve indicates
ought to be deposited, if it represent the
whole truth. But when the temperature of the
supersolubility curve about 10° lower is reached, a
much more copious shower falls by spontaneous
crystallisation, the “labile shower.”
In a closed vessel, such for instance as a glass tube
sealed with the aid of the blowpipe after the introduction
of the solution, on cooling after heating
to a temperature superior to that of saturation,
the first shower never falls at all, no amount of
shaking inducing the deposition of crystals at the
ordinary saturation point, proving that the slight
shower of the experiment in the open vessel is due
to crystal-germs introduced from the atmosphere.
The second shower of crystals falls at the lower
temperature just as before, however, at the temperature
of the supersolubility curve, indicating that
this shower is due in both cases to spontaneous
242crystallisation. Solutions thus enclosed in sealed
tubes, to which inoculating dust crystals cannot
have access, can never be made to crystallise at any
temperature higher than that given by the supersolubility
curve, however agitated, although they
immediately do crystallise, if shaken, as soon as
that temperature is reached during the cooling.
If allowed to remain absolutely quiet, however,
the temperature may fall considerably lower before
any crystallisation occurs, the labile region being
frequently well penetrated before this happens.
When crystallisation does supervene, the temperature
usually rises somewhat. After the labile shower
has been deposited, the crystals continue to grow
steadily further, until the metastable region has
been traversed, and the saturation state is eventually
reached, when final equilibrium is produced.
The proof that the crystals deposited in the
metastable condition were started by the advent
of atmospheric germ crystals—that is, by infinitesimal
but perfectly structurally developed crystals,
carried by their very lightness like the particles of
dust which are only revealed in the path of a sunbeam
as seen against a dark background—was afforded
by a series of experiments with a mixture of two
rare organic chemical preparations, salol (phenyl
salicylate) a substance melting at 42.5°, and betol
(β-naphthol salicylate) another melting at 92°, which
Miers assumed were not likely to be present in
ordinary air. The assumption proved well grounded,
and the first shower never fell at all in the earlier
experiments in which mixtures of these two substances
were allowed to cool in open vessels, from
243the state of fusion. But very soon the air of the
laboratory became impregnated with crystallites
of both substances, due to the very operations
themselves being carried on in contact with the air,
and in the later experiments the first shower of
crystals did fall. The experiments were really
designed to effect the determination of the solubility
curve for salol and betol in each other, that is,
the freezing-point curve of their mixtures, and the
discovery of the so-called “eutectic” point at
which a mixture of constant composition solidifies
at a definite temperature. But incidentally the
experiments also served to establish similar laws
for the production of crystals from the liquefied
state, by cooling below the melting point, to those
applying to crystallisation from solution. In the
case of the mixtures of the substances the one of
lower melting point acted as a solvent for the one
of higher melting point, just as water does for salt.
Two curves corresponding to the ordinary freezing
point and to the limit of superfusion were established,
analogous to the solubility and supersolubility curves.
Pure salol alone proved to crystallise spontaneously
at 33°, 9½° below its melting point, and the refractive
index attained a maximum for this temperature.
Betol spontaneously crystallised at 79°, 13° below
its melting point.
Two general cases of crystallisation are shown
by the dotted curves ABCD and ABE in Fig. 98.
The first, represented by ABCD, is the case of a
supersaturated solution, made by adding the salt
to hot water, being allowed to cool slowly while
stirred. The solution cools from A to B without
244anything visibly happening, no crystal-germ falling
into the solution until B is reached, somewhere well
within the metastable region. When the germ has
fallen in, however, crystals begin to appear as a
slight shower at B, and from B to C they continue
to grow slowly. On reaching the labile condition
at C a cloud of crystals, the heavy shower, is deposited,
and the concentration falls rapidly to D
on the solubility curve, generally with slight rise
of temperature.
The second case is the important one employed
by the author in the investigations which will be
found described in his “Crystalline Structure and
Chemical Constitution” (Macmillan & Co., 1910),
for the purpose of producing crystals of high perfection
for goniometrical investigation. The method
can be confidently recommended as the one best
adapted to afford good measurable crystals, and
is of quite general application. The solution is
made up so as to be in the metastable condition,
that is, only slightly supersaturated for the ordinary
temperatures. Eventually, while the solution is
at rest in a protected place, free from draughts
or vibration, and after it has cooled to the temperature
of the air, a crystal-germ enters, followed
probably by others; each forms a centre of crystal
growth, which proceeds very slowly and deliberately,
keeping pace with the evaporation in such a manner
that the labile condition is never reached. The
natural result is the production of very well-formed
crystals bounded by excellent faces, truly plane
and free from striation or distortion.
When the operation is arranged to occur during
245the night, as will usually be the case, the solution
being set out to crystallise in a quiet and protected
place on the previous afternoon or evening, the slight
fall of temperature during the night gently assists
the process and almost ensures a good crop of a
few well-formed crystals large enough for goniometrical
purposes next morning. They should
be removed before the temperature begins to rise
again with the advent of the sun, dried with blotting
paper and by air exposure for a short time, and
stored in a miniature bottle labelled with the name
or formula of the substance and the date of collection
of the crop. In such cases the labile state is
never reached, and the course of the crystallisation
is represented by the curve BE. The whole conditions
for the curve ABE, however, would correspond
to much lower temperatures, such as those
given at the foot of the diagram below the word
“temperature,” rather than to the upper row of
temperature abscissæ suitable for the other purposes
of the diagram already referred to. Crystallisation
might well begin about 13° or 14°, as shown at B,
and the liquid would cool a couple of degrees or
more during the night while crystallisation was
steadily proceeding, until equilibrium was reached
at E on the solubility curve.
The diagram does not represent any substance
in particular, but is a perfectly general one, corresponding
to the facts observed with most of the
very varied salts worked with by Miers and those of
which the author has had experience. The exact
temperatures and concentrations will, of course,
differ for each substance.
246A beautiful experimental demonstration of
crystallisation from the metastable and labile conditions
of solution respectively is afforded by
potassium bichromate, K2Cr2O7. When deposited
slowly from a metastable solution under conditions
of quietude, this salt is slowly deposited in bright
orange coloured and excellently formed crystals, often
of considerable size, belonging to the triclinic system
of symmetry; they are bounded by good pinakoidal
(pairs of parallel) faces intersecting in sharp edges.
But when the crystallisation occurs from a labile
solution, being much more rapid, it takes the form
of feathery or arborescent branching skeletal growths,
there being inadequate time for the formation of well-developed
crystals.
Fig. 99, Plate XXI., is a photographic reproduction
of well-formed crystals of potassium bichromate,
grown from a solution in the metastable condition
on a microscope slip, just as they are seen through
the microscope in the slow act of formation, employing
a 1½ inch objective. The crystallisation had been
started by germ crystals of the salt falling in from
the air, after which the drop, placed within the
ring of hardened gold size on the slide, had been
covered with a cover-glass, under which the crystallisation
had proceeded with sufficient slowness to
enable a successful photograph to be taken, when
the camera was subsequently attached above the
vertically arranged microscope. An upright micrographic
apparatus had been designed by the author
specially for this photography of growing crystals,
many of the results of which are reproduced in this
book.
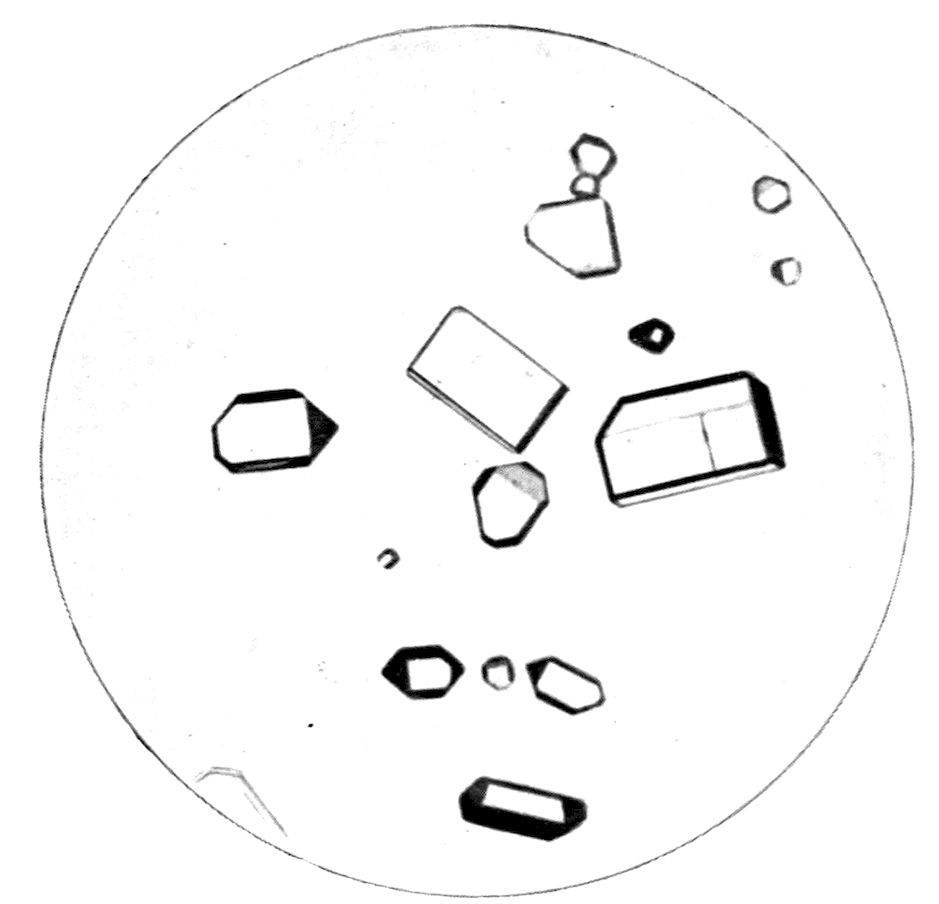
PLATE XXI.
Fig. 99.—Potassium Bichromate slowly crystallising from a Metastable Solution.

Fig. 100.—Potassium Bichromate rapidly crystallised from a Labile Solution.
Characteristic Difference in the Crystals deposited from Metastable and Labile Solutions.
247Fig. 100 is the reproduction of another photograph
taken under similar conditions, but employing a
hot and somewhat more concentrated solution of
potassium bichromate, and making the exposure at
the moment when, in the particular field chosen, a
rapid labile crystallisation was just completing
itself, the rapidity of growth of the feathery skeletal
crystals having just become arrested. Indeed, the
branches are frequently terminated by small well-formed
crystals, the rapid growth having been
succeeded by a final slow crystallisation where the
solution had discharged its labile excess and attained
once more the metastable condition.
This experiment with potassium bichromate lends
itself admirably to lantern demonstration with the
projection microscope. When the drop of hot
concentrated solution is first placed on the warmed
microscope slip, and the latter laid on the stage,
nothing visible on the screen happens for a minute
or two, the solution becoming, however, more or
less rapidly cooled. But suddenly, the drop having
cooled sufficiently to bring the solution to the labile
condition of supersaturation corresponding to the
conditions for spontaneous crystallisation indicated
by the supersolubility curve, arborescent or feathery
growths begin to shoot out from various points in
the field, often near the margin, and traverse the
screen so rapidly that in a moment or two it is
filled with them. The crystallisation then slows
down once more, the labile shower of excess having
become exhausted, and the terminations of the
branches and ramifications begin to develop into
good little crystals, which thus hang like fruit on
248a tree. The experiment is rendered the more
brilliant and beautiful by the bright orange colour
of the crystals.
In Fig. 101, Plate XI., facing page 88, a reproduction
of a photograph of a similar crystallisation from
a labile solution of ammonium chloride is given. This
salt is also particularly suitable for screen demonstrations.
The beautiful skeletal ramifications follow the
axial directions of the cubic axes, ammonium chloride
crystallising in the pentagonal-icositetrahedral class
of the cubic system. Good crystals may, however,
be very slowly grown from metastable solutions,
and they usually exhibit as the principal forms the
icositetrahedron (predominating), cube, octahedron,
rhombic dodecahedron, and the class-distinguishing
pentagonal icositetrahedron. The rapid growths by
spontaneous crystallisation of labile solutions, however,
invariably take the form of the rectangularly
branching feathery crystals shown in Fig. 101.
Further light has been thrown on the act of
crystallisation by another most interesting research
of Miers concerning “vicinal faces,”[21] such as the
three very low pyramid faces (forming a very flat
triakis octahedron) which often replace each octahedron
face on a crystal of alum which has been
grown somewhat rapidly. The author has frequently
observed this phenomenon in the course of the
numerous crystallisations required for the investigation
of the sulphates and selenates. It may be
described in general terms as the replacement of
primary faces possessing the simplest rational
indices by faces having such high indices that it is
249doubtful whether they ought really to be represented
by indices at all. The number of such
vicinal faces which replace the simple face depends
on the symmetry of the crystal, to which, of course,
they conform. Thus, while three such vicinal
faces replace an octahedral face, and two replace
the face of a tetragonal prism, the simple primary
prism face of a rhombic or monoclinic crystal
would only be replaced by one, which may have a
deformation of as much as even 30′ from the correct
position of the prism face, and on either side of it.
Indeed it is possible for a whole succession of such
vicinal faces to be developed within the degree of
arc which may in extreme cases separate the limiting
values on each side of the prism face, and such are
often seen and make up the well-known bundle
of images afforded on the goniometer by a bad face,
a face which would cause the author at once to
reject the whole crystal for measurement purposes.
One of the faces, even in cases such as alum or a
tetragonal crystal, where three or two might have
equal values as regards the symmetry, generally
predominates, and affords a very much more brilliant
image of the goniometer signal than the others in
the bundle, so that an unwary observer might
easily come to the conclusion that this was the
really valid image corresponding to the octahedron
face or to the simple primary prism face, or whatever
particular face was expected in the neighbourhood
indicated by the bundle of images. Obviously,
however, it might only be one of three or two
equally valid faces of a vicinal form, which had
grown predominatingly during the last period of
250growth previous to removal from the mother
liquor.
The explanation of this interesting phenomenon
of the production of vicinal faces is one intimately
connected with the structure of crystals, and it
forms one of the strongest confirmations of the
correctness of the theory of crystal structure the
basis of which is the molecular space-lattice. Miers
is in full agreement with the author in emphasising
the importance of the space-lattice formed by the
“points” representative of the molecules, and
analogously chosen in the molecules. He says:
“Whatever structures may be necessary to account
for other features of crystals, there is little doubt
that we are justified in regarding their faces as the
planes of a space-lattice.”[22] Now Wulff,[23] who has
contributed very considerably to our knowledge of
the nature of the act of crystallisation, has proved,
from his own investigations and those of Weyberg,
carried out at his suggestion in his laboratory at
Warsaw,[24] that faces of greatest reticular density,
that is, those along which the points of the space-lattice
are most thickly strewn, are those which
grow the most slowly, and therefore are the best
developed. This latter will be obvious on a little
consideration, for the faces of less reticular density
which grow more, tend in doing so to extend the
boundaries of the faces of greatest reticular density,
and thus to enlarge those faces. Hence the usual
planes on a crystal must be those of high reticular
density; and these are such as are represented by
251the simplest indices, the faces most dense of all in
points being the primary ones.
But it has been shown from the researches of
Miers that vicinal faces are often produced in
preference to these simple index planes of high
density, and such vicinal faces, although the nearest
(in angular position) of all possible faces to those
simple index planes, are themselves of excessively
low reticular density, so much so that if represented
by indices at all they can only be indicated by very
high numbers, not such as we are accustomed to
consider as in keeping with the simple spirit of the
law of rational indices. Taking the example worked
out most fully by Miers, the octahedral crystals
of alum, it is a fact that the cubic faces of highest
reticular density are those of the cube itself, then
come in order those of the rhombic dodecahedron
and those of the octahedron. Hence, the density
of octahedral faces is very high. But those of the
very low triakis octahedron, which Miers finds to
replace the octahedron faces so frequently as vicinal
faces, are of excessively low reticular density.
Miers explains the appearance of the latter instead
of octahedral faces by assuming that the supersaturated
liquid in contact with the growing crystal
consists of the particles (molecules) of salt uniformly
mingled with those of water, the solvent, and that
the act of crystallisation consists of the escape of
the water and solidification of the salt. Consequently,
the salt particles just before crystallisation
cannot be so dense as they are along primary planes
of the crystal, as they are separated by the water
particles, which are presumably much more numerous.
252Hence it is that they are not deposited along the
planes of high reticular density, but along vicinal
planes of low density of points. For instance, he
shows that the shower of salt particles upon a cube
face would have to be so dense that there would be
insufficient room for the water particles. The
density in a cube face is 114 times as great as that
in one of the vicinal planes observed. Now, 100
cubic centimetres of solid alum weigh 172 grammes,
and 100 c.c. of the solution depositing crystals contain
9·74 grammes of alum. Thus the density of
the growing crystal of alum is nearly 18 times that
of the alum in the adjacent saturated solution.
Consequently the deposition of the salt particles,
in a moderately quick crystallisation, when insufficient
time is afforded for the deliberate escape
of the water particles and for the orderly rearrangement
of the salt particles, occurs along vicinal planes
instead of along the primary planes. For it must
not be forgotten that whenever it has the opportunity
of coming into operation there is a directive
molecular force of some kind, which controls the
operation of crystallisation, and which undoubtedly
attempts to cause, and given adequate time and
scope succeeds in causing, the production of faces
of high reticular density, the fundamentally important
primary faces of lowest indices, and which
are often those along which cleavage occurs.
Wulff emphasises this in saying (loc. cit., p. 461):
“Bei der Krystallisation orientiren sich die Molekeln
auf den Flächen des Krystalles ganz gleichförmig
durch den Einfluss der Richtkraft der Krystallisation.”
The more rapidly the crystallisation occurs,
253however, the less chance is there for this force to
attain its ultimate object. More will be said about
this directive force in the next chapter, after we have
studied the remarkable “liquid crystals” discovered
by Lehmann.
This highly interesting explanation of Miers,
supported as it is by the work of Wulff, and confirmed
also in many respects by the observations
of the author, whose great aim throughout his investigations
has been to avoid the production of such
vicinal faces, throws an important light on the nature
of the act of crystallisation. It renders the reason
clear why crystals which are very slowly grown
from solutions only feebly supersaturated and under
conditions of absolute rest, protected from either air
currents or preventable earth tremors—conditions
which the author has taken quite exceptional pains
to procure for the preparation of the crystals used
in the investigation of the sulphates and selenates
of the rhombic simple salt series and monoclinic
double salt series—are occasionally obtained quite
free from any sign of such vicinal faces. They are
small perfect individuals exhibiting primarily the
faces of high reticular density, that is, the faces of
the simple forms of low rational indices; and these
faces are absolutely plane, affording one single
brilliant image of the goniometer signal, which can
be adjusted with great precision to the cross-wires
of the telescope. For the slower the growth,
the more time is afforded for the escape of the
water molecules, and for the salt molecules to
deposit themselves as directed by the molecular
guiding force of crystallisation, along the planes of
254high reticular density. In many of his experiments
Miers expressly stirred the solution, to prevent
concentration currents, which had been considered
by Wulff of importance in the process, from coming
into play and causing unknown effects. Hence his
experiments in which vicinal faces were produced are
not comparable with the author’s slow growths.
The work of Miers assists in the proof that the
constancy of angle to within one or two minutes
of arc is a real property of the crystals of a substance.
For previously the frequent presence of vicinal
faces rather than the simple forms of high reticular
density, and which had been mistaken for the latter,
had caused Pfaff in 1878[25] and others to conclude
that variations from the true crystal angle amounting
to as much as 30′ were of common occurrence
as the result of strain during deposition.
Brauns[26] in 1887 made a careful series of measurements
of very good octahedral crystals of lead
nitrate, and found 13′ 20″ the largest deviation of
a good image from the theoretical position. He
imputed it to the action of gravity as a disturbing
cause during deposition. The researches of Miers
have cleared away all this misconception, in proving
that the bright images referred to, taken for those
of the simple primary form, are not such at all, but
vicinal faces of very low reticular density.
255
CHAPTER XVI
LIQUID CRYSTALS.
We have seen in the foregoing pages that a crystal
is usually a solid, highly organised in a homogeneous
manner, and, unless the symmetry be developed
to its highest extent, the crystal then belonging
to the cubic system, it is also in general anisotropic,
that is, it exhibits double refraction. Section-plates of it, more or less thin according to the
strength of the double refraction, exhibit colours
in parallel polarised light, and show the phenomenon
of a single optic axis, or of two optic
axes, in convergent polarised light. Every
variety of hardness, however, is displayed, from
that of the diamond down to that of a crystal
as soft as gypsum, and even softer. Moreover,
many of the softer crystallised substances develop
the property of permitting one layer to glide over
another by gentle side pressure with a knife blade,
when inserted in an edge or face in an attempt to
cut the crystal. Calcite and ice, for instance, both
possess such planes of gliding of the structural units
over one another in layers. There are also the
border line cases of crystals so soft as to be readily
bent, and many well-known viscous substances
crystallisable only with great difficulty, some of
which form pliable crystals.
256But in the year 1876 Lehmann discovered a new
property in an already remarkable substance,
iodide of silver, AgI, namely, that at temperatures
superior to 146° C. it can flow like a viscous liquid,
while exhibiting several of the properties which are
characteristic of crystals. Silver iodide is dimorphous,
exhibiting a hexagonal form at the ordinary
temperature, which persists up to 146°. But during
the heating to the latter temperature a regularly
accelerating diminution of volume occurs, the feeble
expansion in directions perpendicular to the axis
being overbalanced by a considerable contraction
along the axis, both quantities having been accurately
measured so long ago as the year 1867 by Fizeau,
by means of his delicate interference dilatometer.
This contraction, so unusual an occurrence with
increase of temperature, culminates at 146°, according
to Mallard and Le Chatelier, in a sudden change
of condition into a cubic modification, accompanied
by absorption of heat. Now Lehmann, studying
this cubic modification of silver iodide under a
microscope which he had devised—specially adapted
for observations at temperatures higher than the
ordinary, by being supplied with the means of
heating the object under observation—found that
it was not only plastic, but actually a liquid.
257

Fig. 102.—Lehmann’s Crystallisation Microscope.
The form of Lehmann’s “Crystallisation Microscope,”
as now constructed by Zeiss, is shown in
Fig. 102. Its essential features are that the glass
object-plate, which is somewhat wider than the usual
microscope 3 by 1 inches slip, is supported by little
metallic columns at a height an inch or more above
the ordinary stage, and may be heated from below
by a miniature Bunsen burner, which is provided
with a delicate graduated gas-tap and is adjustable
for its position, swinging in or out as desired. The
small Bunsen flame may be converted into a blowpipe
flame if necessary, an air-blast attachment to a
mixing reservoir being provided, to which the arm
of the burner is hinged. Two cooling blasts, connected
258with a gas-holder of air, are also provided,
and are adjustable to the most suitable symmetrical
positions above the slide for directing the cooling
air on the part of the latter where the liquid is
situated. These arrangements enable the substance
on the slide to be rapidly or slowly heated or cooled
at will. Electric connections are also provided,
in the event of the observer desiring to study the
behaviour of the liquid crystals under the influence
of the electric current.
Considerably later, in the year 1889, the attention
of Lehmann was called by Reinitzer to another
similarly singular substance, cholesteryl benzoate,
which appeared to consist of an aggregate of minute
crystals which flow as readily as oil, while preserving
many of the characters of crystals.
In the next year, 1890, the substance para-azoxyphenetol,
then recently discovered by Gattermann,
was observed by Lehmann to form a turbid “melt”
on fusion, which consisted of an aggregate of crystals
flowing with a mobility equal to that of water,
and which take the form of spherical drops showing
a dark kernel inside, as shown at a in Fig. 103, quite
unlike a drop of ordinary liquid. The kernel disappears
on shaking, but reappears on coming to
rest again. In polarised light the drops show
dichroism, that is two different colours in different
parts or directions, being divided into white and
yellow parts, the yellow as a pair of opposite approximately
60°-sectors, as indicated at c in Fig. 103.
Under crossed Nicols they show a black cross, as
represented at d in Fig. 103.
Now obviously these drops are doubly refractive,
259and their whole optical behaviour corresponds to
the arrangement of the molecules in concentric
circles, such as that suggested at b in Fig. 103.
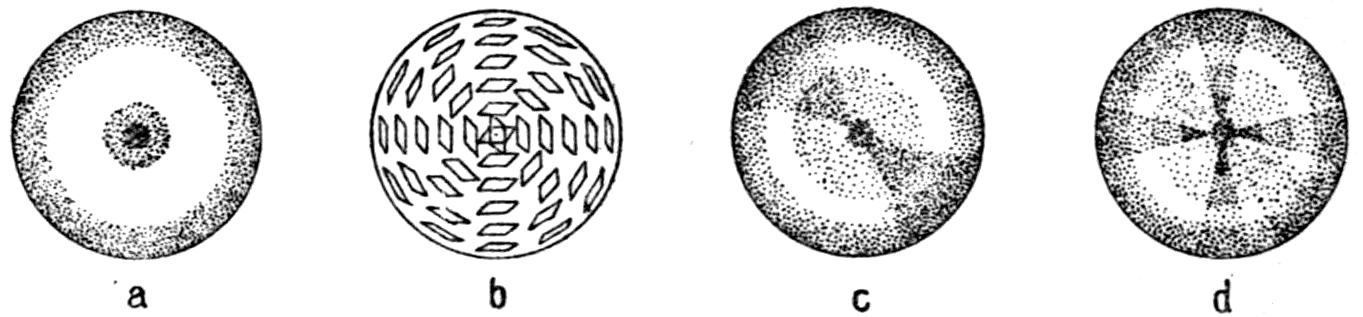
Fig. 103.—Liquid Crystals of Para-azoxy-phenetol arranged in Spherical Drops.
Another substance of like character, para-azoxy-anisol,
was subsequently found to behave similarly,
and forms an excellent substance to use for demonstration
purposes. A reproduction of a photograph,
kindly sent to the author by Prof. Lehmann, of a slide
of this substance is given in Fig. 104, Plate XXII. It
shows a characteristic field of such drops, exhibiting
white parts and yellow sectorial parts which photograph
dark, of para-azoxy-anisol mixed with a little
para-azoxy-phenetol, oil and resin (colophony), as seen
under the polarising microscope with crossed Nicols.
The next and possibly most interesting step in
this remarkable series of discoveries was made by
Lehmann himself in the year 1894. He alighted
on the fact that ammonium oleate, crystallised
from solution in alcohol, affords a splendid example
of flowing crystals, which are sufficiently large to
enable their habits to be studied in detail. The
individuals are almost invisible in ordinary light,
owing to the refractive index of the crystals and of
the mother liquor being approximately the same.
But in polarised light, using crossed Nicols, they
260are clearly revealed as steep double pyramids
with more or less rounded edges. Their section
is nearly circular in consequence, and they exhibit
optical properties of a uniaxial character, the optic
axis being that of the double cone or bipyramid.
A characteristic individual is shown at e in Fig. 105.
When two of these flowing crystals approach each
other, as at a in Fig. 105, they coalesce to form a
larger single individual, as is indicated in stages at
b, c, and d in the illustration.
Fig. 105.—Liquid Crystals of Ammonium Oleate.
When the cover-glass, under which they are
growing on a microscope 3 by 1 inch slip, is moved
to and fro so as to distort these remarkable bodies,
which we may well hesitate to call crystals, the
singular effect is produced of causing them all to
become similarly orientated, for the extinction directions
follow the direction of the pressure. They at
once seek to regain their original form, however,
on cessation of the disturbance. A slide of the
bipyramids under pressure is shown in Fig. 106.
In the black extinguished portions of the field the
261flowing crystals are flattened, according to Lehmann,
and arranged so that the optic axis is in all cases
perpendicular to the tabular crystals and the glass
plates and parallel to the axis of the microscope.
The black parts are separated by oily strips, as shown
in another slide under considerable pressure, represented
in Fig. 107, which are composed of the tabular
crystals standing on end, with their optic axes
parallel to the plates. These strips polarise the more
brightly the more truly the crystals stand perpendicularly
to the plates. The two conditions are
shown diagrammatically at a and b in Fig. 108.

Fig. 106.—Liquid Crystals of Ammonium Oleate under slight pressure.
Fig. 107.—Ammonium Oleate under considerable pressure.

Fig. 108.—Diagrammatic Representation of Arrangement of Molecules.
Lehmann believes the explanation of these singular
phenomena to be that the “liquid crystals” of
ammonium oleate are composed of piles or layers of
thin plates perpendicular to the optic axis. Disturbance
detaches the plates from their piled positions
over one another, and sets them parallel to the glass
262plate, except in places, the oily strips, where the
plates stand upright, perpendicularly to the micro-slip
and cover-glass. Lehmann, indeed, goes
further, and asserts that the molecules themselves are
anisotropic, and probably take the form of plates.
Fig. 109.—A Crystal of Ammonium Oleate A, broken at B, each part repairing itself at C, perfect again at D.
An extremely interesting experimental observation
of Lehmann’s with the bipyramids of ammonium
oleate is, that if one of them, for instance A in
Fig. 109, be broken into two parts, as at B, each part
grows again and completely repairs itself, becoming
once more a perfect double pyramid, as indicated in
stages at C and D in the figure.
Fig. 111.
Cruciform, Boomerang, and Arrow-head Twins of Ammonium Oleate.

PLATE XXII.
Fig. 104.
Dichroic Crystal Drops of Para-azoxy-anisol.
Fig. 112.
Rectilinear Liquid Prisms of Para-azoxy-benzoic Acid.

Fig. 115.—Tetragonal Astatic Magnet-system.

Fig. 116.—Cubic Astatic Magnet-system.
263Twins of ammonium oleate are also shown in
Figs. 110 and 111, the former figure representing a
twin of cruciform character, and the latter exhibiting
twins resembling a boomerang and an arrowhead
respectively.
This substance, ammonium oleate, thus appears
to be one of the most remarkable and interesting
of all the bodies yet observed to afford liquid crystals.
Many other oleates produce liquid crystals also,
but the ammonium salt is by far the most striking,
and very convincing as to the reality of Lehmann’s
discovery.
Another substance of a different nature was
discovered by Vorländer in the year 1904, namely,
the ethyl ester of para-azoxy-benzoic acid. A characteristic
microscope slide of it in ordinary light
is shown in Fig. 112, Plate XXII., which is a reproduction
of an actual photograph most generously
sent to the author by Prof. Lehmann.
The individuals are described by Lehmann, who
further studied the nature of the substance, as
almost perfectly rectilinear prisms with nearly
sharply defined basal plane end faces. A singular
fact about this substance is, that when two individuals
approach each other they arrange themselves
parallel with a jerk, and then flow into each
other, producing a single larger liquid crystal, and
often with such rapidity that the eye can scarcely
follow the movements. These coalescences appear
to be occurring all over the field at once, with the
production of larger and larger crystals. Indeed,
Lehmann likens it to a struggle between the innumerable
individuals, in which the smaller ones
are being continually eaten up by the larger.
Vorländer also prepared the ethyl ester of para-azoxy-cinnamic
acid, and Lehmann found it to be
264similarly interesting. The substance separates
from a solution in monobromonaphthalene in uniaxial
prisms or hemimorphic pyramids, the edges
and solid angles of which are more or less rounded,
and which appear colourless in the direction of the
axis and yellow in all other directions. When
pressed between the cover-glass and the micro-slip
on which the crystallisation is proceeding, extinction
of the light occurs throughout the whole mass when
polarised light is being employed and the Nicols are
crossed. For throughout the entire substance the
particles—whether they are the molecules themselves
as Lehmann asserts or aggregations of them
in the form of ultramicroscopic crystals—arrange
themselves with their optic axes (the crystals being
uniaxial) perpendicular to the cover-glass and
micro-slip, as in the case of ammonium oleate.
Lehmann’s theory is that the molecules themselves
are tabular perpendicular to the axis, as in the case
just referred to, and that they are thus readily
coerced by the pressure of the flat cover-glass to
take up positions parallel to it.
Two further reproductions of photographs, taken in
polarised light, of a somewhat remarkable character,
which have been placed at the author’s disposal by
the courtesy of Prof. Lehmann, are given in Figs.
113 and 114, Plate XXIII. Fig. 113 represents
numerous doubly refractive and dichroic strips
marking the boundaries of elongated individual
crystals of the substance dibenzal benzidine, and
affords a graphic idea of the real character of the
double refraction displayed by liquid crystals.

PLATE XXIII.
Fig. 113.—Elongated Liquid Crystals of Dibenzal Benzidine, showing Double Refraction and Dichroism.

Fig. 114.—Spherical Liquid Crystals of Para-azoxy-anisol, showing Interference Colours under Crossed Nicols as the Effect of Compression.
265Fig. 114 represents the effect of compression on
para-azoxy-anisol, and demonstrates very clearly
the distribution of the interference colours due to
double refraction.
We are thus face to face in these remarkable
experiments with some new facts concerning the
nature of crystals. For we pass here into the
borderland between ordinary liquids—singly refractive
and structureless, in which the molecules
are rolling over each other with every possible
orientation—and solid true crystals possessing
homogeneous structure, and the basis of which
is a space-lattice arrangement of the chemical
molecules, determinative of the system of symmetry
displayed. In this wonderful borderland we certainly
have had revealed to us, by the genius and
persistency of Lehmann, liquids which possess
many of the attributes of crystals, such as definite
orientation of the ultimate particles, double refraction,
and optic axes. These are undoubtedly
solid facts which require to be faced.
Whether Lehmann’s theory is to be accepted in
full can only be decided after much more investigation
by several independent investigators. We are
now becoming familiar with the phenomena, as
they have naturally excited immense interest in
all scientific circles, and demonstrations of many
of the experiments of Lehmann have been given
in this country by Dr. Miers, Prof. Pope, and others,
and particularly by Messrs Zeiss, with their new high
temperature microscope, a description of the use of
which for the projection of liquid crystals on the
screen will presently be given. Prof. Lehmann himself
has described the phenomena so clearly and fully
266that it is quite easy for others to repeat his experiments,
and doubtless time would often be much
better spent in doing so than in criticising points of
theory without observing the phenomena at first
hand. It frequently happens, in the inevitable
march of scientific progress, that striking new
facts, such for instance as the discovery of the
composite nature of the chemical atom, are apt to
cause either alarm, even panic, as to cherished
theories, or else unreasoning scepticism. The happy
mean between these two modes of receiving such
facts, the open philosophic mind, ever ready to
widen the scope of the horizon when a novel supposition
is indubitably proved to be a real fact, and
to assimilate that truth into the theory, widening
correspondingly the scope of the latter if needful,
is obviously the ideal thing to cultivate, and one
which eventually finds itself in harmony with the
authenticated final results of the new discoveries.
It usually happens that too sweeping conclusions
are at first drawn from such new facts, but time,
with its further wealth of experience, especially
the accumulation of experimental data which it
brings in its train, soon levels these down and relegates
the facts to their proper positions in the great
scheme of natural knowledge.
Lehmann’s view is that the ordinary effect of
surface tension to cause truly liquid particles to
assume the spherical “drop” form is resisted by
a special force, which he terms “Gestaltungskraft,”
and which we may perhaps translate “Configuration-determining
force.” This force he considers is not
identical with that of elasticity, but is that force
267by virtue of which a “flowing crystal” continually
seeks, while freely swimming in the mother liquor
or fused liquid, to take up its normal configuration.
Even if a spherical drop could be cut out of it, the
sphere would at once become a rod, prism, or pyramid
or whatever the normal configuration of the flowing
crystals of the substance in question might be.
The much debated term “liquid crystal” has
been given by Lehmann to the normal configuration
of each of the now considerable number of substances
which have been discovered to exhibit the
phenomena of flowing crystals. The latter appellation
“flowing crystal,” which Lehmann also uses, appears
to the author to be in many ways more suitable,
however, and would avoid much of the criticism
which has been levelled at the term “liquid crystal.”
As already indicated, Lehmann attributes the
whole phenomena to a fundamental cause, namely,
anisotropy (optical dissimilarity in different
directions) of the molecules themselves, which he
considers must cause self-restoration of the structure
after disturbance, a process which he terms “spontaneous
homœotropy.” He considers that it is
the molecular configuration-producing force, connected
with the tabular form of, and directionally
differentiated distribution of energy and force in, the
single chemical molecules, which maintains the inner
structure of the flowing crystal in position. The
polyhedral outward form thus appears to be a
necessary consequence of the inner structure, on this
basis that it is a force resident in the molecules
themselves which produces the structure.
Now the revelation of new facts, as startling as
268those which are now experimentally fully confirmed
concerning flowing crystals, must inevitably cause
searching reflection as to whether the magnificent
geometrical work on the 230 homogeneous structures,
and their development in actual fact in the 32
classes of crystals, is to stand or to be seriously
affected. Again the author ventures to express
the opinion, that just what happened in regard to
the historic differences between the schools of Haüy
and Mitscherlich, will in all probability again occur,
namely, both extreme views will be shown to depend
more or less on real facts, and other connecting
facts will eventually be revealed which will completely
reconcile the two series with each other.
In the author’s opinion, the geometrical work will
stand, as the grand generalisation it really is. But
it will be interpreted in the future without the
somewhat arbitrary assumptions which have more
or less accompanied it. From these it will be freed,
and then rise purified and elevated to its real
dominating position in regard to crystal morphology.
Lehmann, with the natural enthusiasm of the
discoverer of one of the most remarkable facts for
which the last few decades have been famous, may
have carried his theory too far, and particularly
in that part of his work, to which the author has
not hitherto referred, in which he describes certain
phenomena of flowing crystals as akin to the movement
of living organisms such as bacteria, and thus
brought even some of the sound facts under the
criticism of the sceptic more than might otherwise
have been the case. He may also have made his
theory far more revolutionary than is essential.
269But the one incontrovertible thing stands out plainly,
namely, that the “flowing crystals” with which he
has made us acquainted are an indubitable experimental
fact. Flowing crystals are produced, however,
by a relatively few substances of very complex
molecular constitution, involving a large number of
atoms in the molecule; they are mostly compounds
of carbon, and in number possibly not one per
cent. of the innumerable substances known to
produce ordinary solid crystals. That the theory of
crystal structure can eventually be made to include
these few remarkable substances is highly probable,
when many more facts have been accumulated.
Lehmann would appear to have made one point
very clear, which at once removes an objection long
felt by the author to the theory of crystal structure
as it stands at present, namely, that the chemical
molecule is endowed with a directive orientative
force, which is certainly concerned in crystallisation.
To assume, as has been done, just because it is not
necessary from the point of view of the geometrician
in developing his possible homogeneous structures,
that no directive force is operative in crystallisation,
and that all is a mere question of the most convenient
mechanical packing of the molecules, is, in the
author’s opinion, going beyond what the experimental
facts justify. If Lehmann’s discovery of
flowing crystals does nothing more than return to
the molecule the property always hitherto attributed
to it, of possessing in itself some directive force by
reason of which it arranges itself homogeneously
by mutual accommodation with its similarly endowed
fellow molecules, when its motion in the liquid
270state has been sufficiently arrested by its approach
to its fellows within the range of molecular action
(four or five molecular diameters), either by cooling
or the falling out of previously separating solvent
molecules, it will have achieved a notable thing.
What does occur at the moment of crystallisation
is at the present time one of the most interesting
unsolved questions in crystallography, and one
calling most urgently for solution. Attention was
directed to the problem in the last chapter, in connection
with the suggestive work of Miers on vicinal
faces. It was shown that it was only when the
directive force had time to come properly into
operation that the primary faces of fundamental
importance were produced, and that when the
crystallisation was rapid vicinal faces formed
instead. Lehmann believes that a single kind of
chemical molecule is only capable of producing a
single specific space-lattice, and that polymorphism
is due to alteration of the molecules themselves at
the critical temperature of transformation. He
showed so far back as 1872 that this limit could be
actually observed under the microscope, as a definite
line of demarcation between the two varieties as
the temperature fell, one side of the field attaining
the critical temperature slightly before the other,
and the defining line between the two kinds thus
travelling over the field. Internal friction did not
appear to Lehmann to enter into the question at
all, as he considered it would have done if a rearrangement
of the molecules were the sole cause
of the change. The molecules themselves, he states,
must have been undergoing change, and such rearrangement of them as occurred must have been
due to that fact.
PLATE XXIV.
Fig. 117.—Arrangement of Astatic Magnet-systems in a Plane.

Fig. 118.—Arrangement of Astatic Magnet-systems in Space.
271Lehmann suggests a very interesting explanation
of the molecular orientative force of configuration,
namely, that it is due to the action of the electronic
corpuscles (forming the elementary atoms) rotating
in the molecule. For the molecules of flowing crystals
behave like freely suspended astatic systems of
magnets, which are constantly setting themselves,
even while moving about, in a crystalline space-lattice.
He suggests that the molecules are really magnets
the poles of which mutually attract and repel one
another; that two equal magnetic molecules are
arranged alongside with opposite poles against each
other, thus mutually binding each other, or that four
horse-shoe magnets may be arranged with opposite
poles together, in a tetragonal astatic system, as
shown in Fig. 115, Plate XXII. The latter may be
grouped in space in a cubic astatic system, as represented
in Fig. 116 on the same Plate; while Figs. 117
and 118, Plate XXIV., are further suggestive of how
a homogeneous structure of such astatically distributed
molecules can be built up, Fig. 117 representing
a single plane of them, and Fig. 118 the
complete arrangement in space.
An astatic system of molecules of this nature
would have lost all power of attraction by a magnet,
and the fact would thus be accounted for that no
striking crystallographic results have ever attended
experiments on crystallisation in a magnetic field.
Astatic systems, however, such as that shown in
Fig. 115, would certainly arrange themselves in space-lattices.
For such parallel arrangements would, in
272general, involve differences in different directions,
with regard both to internal friction and to the
power of thermal expansion and of such regular
dilatational or other deformational changes as we
know are provoked by different physical conditions
of environment. These differences would naturally,
in turn, give rise to external polyhedral form.
Lehmann then goes on to point out that either
electric currents or mechanically moved quantities
of electricity, such as moving negative electronic
corpuscles, can give rise to just such magnetic
effects, and he suggests that these corpuscles are
the true cause. He supposes that the directive
forces result in astatic combinations which find
their equilibrium when the latter have taken up
their positions at the eight corners of a cube or
other elementary parallelepipedon of one of the
fourteen possible space-lattices, the positive atoms
being encircled spiral-wise by the negative electronic
corpuscles in alternately opposite directions. Such
parallelepipeda would seek homogeneous repetition
by virtue of the fact of the corners exhibiting
alternating polarity.
These theoretical ideas of Lehmann have naturally
called forth much discussion, criticism, and
scepticism. But, so far, his experimental facts
have been fully substantiated by further investigation.
Much more practical work is urgently
required, however, before the subject can be considered
as laid on a secure foundation. So much
may be said, however, that it is clear that we must
concede the existence of a directive force of crystallisation,
and not be led by the pure geometry of
273the subject of crystal structure to ignore facts of
such interest and undoubted importance as have
been brought into prominence by the remarkable
work of Lehmann.
A further interesting contribution has recently
been made by Vorländer[27] to the facts regarding
the relationship between chemical constitution and
the formation of liquid crystals. It must have
already struck the reader that most of the substances
which exhibit liquid crystals are composed of a large
number of chemical atoms, being either long-chain
compounds of the fatty acids or complex derivatives
of the hydrocarbon benzene, C6H6; also that many of
the latter are “para” compounds, that is, derivatives
in which the substitution groups are inserted in the
benzene ring of six carbon atoms in the “para” position,
which is that at the opposite corner of the
hexagon to the carbon atom to which a substitution
group has already been attached. This renders the
para compounds the most extended in a straight line
of all the benzene derivatives. Now Vorländer finds
that a particularly favourable condition for the production
of liquid crystals is a linear structure of the
molecule. As the para substitution products of
benzene derivatives possess this elongated structure,
many of them exhibit the development of liquid
crystals. The more linearly extended the structure
becomes, that is, the longer the straight chain of
atoms is, the more favourable become the conditions.
The advent of a third substitution group, however,
which would have the effect of producing a kink in
the chain, or of bending it, appears to destroy the
274possibility of the production of liquid crystals.
This interesting observation may afford the key
to many of the extraordinary phenomena of liquid
crystals which have been described, and is undoubtedly
one of prime importance. Further
favourable conditions for the formation of liquid
crystals, according to Vorländer,[28] are the aromatic
character, and the presence of the doubly-linked
carbon and nitrogen groups C:C, C:N, and N:N,
which are usually so rich in energy.
The idea of the formation of a specific crystalline
homogeneous structure, merely because the
mechanical fitting-in of the molecules occurs with
the minimum of trouble or maximum of ease for
this particular type of all the 230 possible types,
is certainly not applicable to the case of Lehmann’s
liquid crystals. With this, moreover, is also connected
the question of softness or hardness of crystals,
which was referred to at the opening of this chapter.
For the so-called liquid crystals are extreme cases
of softness, and yet in these cases the molecules
must still be arranged in accordance with the
internal structure of a crystal, either parallel or
enantiomorphously definitely orientated with respect
to each other, for otherwise it is not possible
to account for the optical properties resembling
the orientated ones of a crystal. Yet the condition
being that of a liquid, the molecules must be able
readily to pass and roll over each other, and
hence cannot be at the close quarters where mere
“fitting-in” comes into play.
Again, as has been pointed out earlier, many soft
275crystals, even such as calcite, which are only relatively
soft, attaining the position of as much as four in the
scale of hardness, readily exhibit the property of
being deformable upon glide-planes. The molecules
in these cases have been shown to undergo a movement
which has two components, a transference and
a rotation, a fact which has been thoroughly substantiated
by optical investigations of the parts
of the crystal concerned before and after gliding.
There cannot, therefore, have been merely “fitting-in”
of the molecules, but their orientated positions
must have been determined and maintained by the
organising force, which is probably purely physical
and not chemical, but is nevertheless the cause of
crystallisation; it draws the molecules within a
certain range of each other, corresponding to and
dependent upon the temperature, causes or enables
them to arrange themselves in the marshalled order
of the particular type among the 230 possible
arrangements, and keeps them at the same time from
approaching nearer to each other than within these
prescribed limits corresponding to the temperature.
It is doubtless within these limits that gliding
can occur parallel to such planes as leave the molecules
most room for the purpose, and which are
directions of least resistance.
276

Fig. 119.—Lehmann’s Crystallisation Microscope arranged for Projection.
Connected with this important question is the
principle enunciated by Bravais, as a result of his
discovery of the space-lattice, that cleavage occurs
most readily parallel to those net-planes of the
space-lattice which are most densely strewn with
points. The force just referred to, whether we
term it cohesion or otherwise, is obviously at a
maximum within such a plane, and at a minimum
in the perpendicular direction where the points
are further off from each other. Moreover, it has
been fairly well proved also, from the experiments
277of Wulff, described in the last chapter, that the
direction or directions of maximum cohesion are
those of slowest growth of the crystal; so that faces
parallel to those directions become relatively more
extended owing to the more rapid growth of other
faces on their boundaries, and thus become the most
largely developed and confer the “habit” on the
crystal. All these are facts so important as evidences
of a controlling force at work in crystallisation,
that a purely geometrical theory of the formation of
crystals which would make “facility of fitting-in”
of the molecular particles its chief tenet, obviously
does not tell us the complete story. Hence the
author desires to utter a warning against going too
far with the pure geometry of the subject. The
geometricians have done a grand work in providing
us with the thoroughly well established 230 types
of homogeneous structures, as a full and final explanation
of the 32 classes of crystals, and so far
their results are wholly and unreservedly acceptable.
The phenomena of “liquid crystals” lend themselves
admirably to screen demonstration, for which
purpose an excellent improved form of the crystallisation
microscope of Lehmann, shown in Fig. 119,
is constructed by Zeiss, and its actual use in the
projection, with the aid of the well-known Zeiss
electric lantern, but specially fitted for the purpose,
is shown in Fig. 120.
A magnification of 600–700 diameters on the screen
is very suitable, employing a Zeiss 8–millimetre
objective without eyepiece. This objective affords
directly a magnification of 30 diameters. For
ordinary eye observation an eyepiece magnifying
6–8 times is added, thus affording to the eye a
magnification of about 200 diameters.
278

Fig. 120.—Zeiss Apparatus for the Projection of Liquid Crystals.
279The lantern is supplied with a self-feeding electric
arc lamp, ensuring a steady light. A collective
lens of extra light-gathering power is fitted in front as
condenser, and from it proceeds a light-tight tube provided
with a water cell to filter out most of the heat
rays which accompany the light. The electric lantern
with Brockie-Pell or Oliver self-feeding arc lamp,
shown in Figs. 71 and 79 (pages 186 and 202), is
also equally suitable, and with the water cell, and
parallelising concave lens removed from the large
Nicol polariser, affords a parallel beam of the same
character as the Zeiss apparatus. The microscope
stands on a sole plate provided with levelling screws,
and is naturally employed in the vertical position
for such work with fused substances. A mirror
inclined at 45° at the foot of the microscope directs
the parallelised rays from the optical lantern through
the microscope, and another above the optical tube
reflects them to the screen.
The heating apparatus consists of a form of
miniature Bunsen burner fitted with blowpipe blast,
the respective pressures of gas and air being regulated
by means of two taps with graduated arcs for obtaining
greater delicacy of adjustment. The tabular
plate seen to the left in Fig. 119 is the graduated
semi-circle of the two taps; below it is seen the
cylindrical mixing chamber for gas and air, in the
event of the necessity for using the Bunsen as a
blowpipe. There are two separate attachments
for indiarubber tubes to this cylinder, conveying
respectively gas and air. Above the object stage
280a double air-blast is fitted, each tube of which is
hinged with a universal joint, so that it can be
readily adjusted to any desired position on either
side of and above the glass plate (supported on little
metallic uprights) on which the experiment is
being conducted. A polarising Nicol prism and an
analysing Nicol, both constructed in a manner
which protects them from the effects of heat more
effectually than is the case with the usual form,
are provided for obtaining the projections in polarised
light. The objective and analysing Nicol, as well
as the substage condenser, are also specially protected
from injury by heat, by being surrounded
with a water jacket, supplied with running water,
and a disc-like screen just above the objective
assists in deflecting the heat rays from the optical
tube and its Bertrand lens and other usual fittings.
The miniature Bunsen flame is usually brought about
an inch below the object-plate, and the size of the
flame can be regulated with the utmost precision,
so that a fairly constant temperature can be obtained
for a considerable time. With the aid of the blowpipe
air-blast temperatures up to 700° C. can be
safely employed.
The microscope shown in position on the projection
apparatus in Fig. 120 is a still more recent
form introduced by Zeiss, embodying several further
conveniences and improvements.
The following substances lend themselves particularly
well to projection purposes. Para-azoxy-anisol
with resin, which exhibits the phenomenon
of rotating drops; cholesteryl acetate, which affords
a fine example of spherical liquid crystals; paraazoxy-phenetol
281with resin, which gives beautiful interference
colours; and the acetyl ester of para-azoxy-benzoic
acid with resin, which shows the uniting
of crystals to form larger and larger individuals.
Perhaps the most interesting and beautiful of
all is cholesteryl acetate, a characteristic field of
which is shown in Fig. 121 on Plate XVI., facing
page 208. It is interesting that on this Plate XVI.
there are represented the very hardest and the
softest of crystals, namely, diamonds and liquid
crystals. In order to obtain the finest effect the
heating and cooling should be carried out very
slowly. The little Bunsen burner, with a very
minute flame, is first placed under the slide,
and allowed to act until the substance melts
and forms a clear liquid. The gas jet is then removed
and the air-blasts, both of which are simultaneously
actuated when the tap controlling them
is turned, are very gently brought into operation,
one on each side of the centre of the slide, there
being a good working distance of a quarter of an
inch or more between the slide and the objective.
The cooling is thus brought about very slowly.
The Nicols should be crossed, and at this time the
field is quite dark, the liquid substance being at
this temperature (well above 114.5° the ordinary
melting point) an ordinary singly refractive liquid.
As soon as the temperature has become reduced
to that at which the particular modification of cholesteryl
acetate is produced which forms liquid crystals,
spots of light make their appearance at various points
in the field, and each expands into a beautiful circular
and more or less coloured disc marked by a rectangular
282sectorial black cross, which latter is well
shown in the illustration (Fig. 121). These beautiful
apparitions continue to occur, and each to expand to
a certain size, which is rarely exceeded, until the whole
field becomes filled with the wheels or crossed discs, the
general effect very much in some respects resembling
that afforded by a slide of the well-known polarising
substance salicine. These discs, however, are
liquid, being spherical drops, of the structure
already described and illustrated in Fig. 103, and
that this is so is at once made apparent on touching
the cover-glass with a pen-knife or other hard pointed
substance, which immediately causes them to become
distorted. They recover instantly their shape again
when the pressure is removed. When the cooling,
moreover, has proceeded still further, there is a
sudden change, and acicular solid crystals shoot
over the screen, tinted with all the colours of the
spectrum, until the field is full of them, the ordinary
solid modification of the substance having then been
produced. The experiment may be repeated with
the same specimen of the substance, mounted on
the same slide, covered with the usual thin cover-glass,
time after time for months, at reasonable
intervals.
In concluding this chapter it may be mentioned
that absolute proof of the double refraction of the
liquid crystals of several different substances, derivatives
of cinnamic acid, has been afforded during the
year 1910. For direct measurements have been
carried out by two independent investigators, Dorn
and Stumpf, of the two refractive indices corresponding
to the ordinary and extraordinary rays in each
case, the crystals being uniaxial.
283
CHAPTER XVII
THE CHEMICAL SIGNIFICANCE OF CRYSTALLOGRAPHY. THE THEORY OF POPE AND BARLOW—CONCLUSION.
Nothing in connection with the subject of crystallography
is more surprising than the neglect and
apathy with which it has been for long treated by
the chemical world. That crystalline structure
is intimately related to chemical constitution will
have been made abundantly plain during the course
of this book. Yet in spite of the great work of
Mitscherlich, essentially a chemist, and of a large
amount of striking work which has been steadily
accumulating during the last thirty years, with
results of vital importance to chemistry, it is only
at the eleventh hour that chemists are really
awakening to the vast significance which crystal
structure has for them.
The explanation undoubtedly is, that the long
interregnum of conflicting investigations, doubt,
and controversy, which followed the work of Haüy
and Mitscherlich, and preceded the beginning of
really accurate and painstaking investigation of an
organised and systematic character, had caused
chemists to regard with more or less of indifference
the work of the crystallographers. Added to this
we must remember that the subject of crystallography
has hitherto been taught, when taught at
284all, merely as an appanage of mineralogy, although
the pure chemical substances which crystallise
well infinitely outnumber the naturally occurring
minerals, and the results afforded by them frequently
possess a much greater value by reason of the purity
of the substances and their more definite chemical constitution.
Also the mathematical and geometrical side
has usually been unduly emphasised, and carried on
in lectures without any practical goniometrical work
at all. Moreover, the current text-books have
often proved forbiddingly full of calculations
and formulæ, and of the obsolete and unenticing
symbols of Naumann.
At last we have come to see that the subject
is one of fascinating interest when its study is
commenced in a practical manner from the beginning,
armed from the very first lesson with the
goniometer. The crystal itself is then our main
and highly interesting study; its exterior form
unravels itself in a most delightfully simple manner
when we follow the arrangement of its faces in
zones on the goniometer itself; and its symmetry
becomes immediately patent to our eyes in all
ordinary simple cases, when we construct for ourselves
its plan in a stereographic projection, drawn
at first in freehand while still at the goniometer.
The calculations also become perfectly simple
when we have learnt that only the simplest of the
very easy formulæ of spherical trigonometry are
required, and which a knowledge of only elementary
plane trigonometry enables us to apply. Aided by
a few very helpful rules, such as those of Napier
for calculating right-angled spherical triangles,
285and the rule of the anharmonic ratio of four poles
in a zone—which, when the positions of three
crystal faces of the zone are known, at once enables
us to calculate the situation of any fourth face of
the zone—we have at once a stock-in-trade which
carries us over all difficulties in the way of calculation,
and relegates this side of the work to an altogether
subordinate position, although accuracy in carrying
it out is, of course, absolutely essential and even
vital.
Especial interest has recently been attracted
on the part of chemists to the bearing of crystallography
on their science by a remarkable theory
which has been advanced by Pope and Barlow,
connecting the internal structure of crystals with
chemical valency, the power which the atom of a
chemical element possesses of combining with the
atoms of other elements, and which is generally
expressed by the number of atoms of a monad
element, such as hydrogen or chlorine, with which
it is capable of combining chemically. Thus the
electro-positive metal potassium is said to have monad
valency because it is capable of combining with one
atom of the electro-negative element chlorine to form
the salt potassium chloride, KCl; calcium possesses
dyad valency because it can unite with two atoms
of chlorine to form calcium chloride, CaCl2; aluminium
is triadic as it can combine with three atoms of
chlorine producing aluminium chloride, AlCl3; carbon
is a tetrad because it can take up four chlorine atoms,
forming carbon tetrachloride, CCl4, and phosphorus
a pentad as it can fix five with production of phosphorus
pentachloride, PCl5; while sulphur is a hexad
286because it can take up as many as six atoms of
chlorine, forming sulphur hexachloride, SCl6.
Occasion has already been taken in Chapter XI. to
refer to the able work of Prof. Pope with regard to
optically active carbon compounds, and in Chapter
IX. the important contribution of Mr Barlow to
the completion of the theory of the homogeneous
partitioning of space has likewise been discussed.
In collaboration these two investigators have now
propounded a theory which connects the chemical
and geometrical sides of crystallography in a
somewhat startling manner, which has naturally
aroused very considerable discussion, and which,
whether right or wrong, cannot fail to have the
best results in attracting investigators to the
subject.
Starting from the facts which have now been laid
down in this book as having been firmly established
by the most careful measurement and experimental
investigation—notably the constancy of the interfacial
angles of the crystals of the same substance,
the fixed positions of the atoms or their spheres of
influence in the molecule and in the crystal, and the
arrangement of the molecules in space-lattices and the
atoms in point-systems—Pope and Barlow assume
that valency, the expression of the relative combining
power of the chemical elements, is a question of
the size of the sphere of influence of the atom of
an element, and that the relative sizes of such spheres
of influence determine the modes in which they can
be packed, that is, the nature of the homogeneous
crystal structure which they can build up. The theory
consequently renders the chemical phenomenon of
287valency and the physical phenomenon of crystalline
form mutually interdependent.
It will thus be apparent that the essence of their
conception is that the chemical molecule may be
considered as made up of a number of spheres
corresponding to, and representing, the spheres of
influence of the atoms composing it, and that the
volume of each sphere is roughly proportional
to the valency of the atom which it represents.
They then assume that the sum of the valencies of
the atoms present in the molecule may be substituted
for the molecular volume, and the quantity
thus arrived at is termed by them the “valency
volume.” By using the valency volume instead
of the molecular volume in the author’s formulæ
for calculating the molecular distance ratios, which
have been shown in Chapter X. to afford the relative
dimensions of the unit cell of the space-lattice, and
the distances of separation of the centres of gravity
of the molecules from each other along the directions
of the crystal axes, Pope and Barlow arrive at new
ratios, which they term equivalence parameters.
By the use of these latter they have attempted to
account for the crystalline structure of a number
of substances—chiefly organic compounds, in the
investigation of which Prof. Pope has proved so
adept—which are connected morphotropically in the
manner described in Chapter VIII., and of others
which are still less intimately connected.
Unfortunately, the equivalence parameters do
not make clear the relationships in an isomorphous
series, as do the molecular distance ratios; for they
are, from their very nature and mode of derivation,
288almost identical for all the members of an isomorphous
series, the valencies of the interchangeable
elements being the same. The molecular distance
ratios have also the great advantage of being derived
from the three measurements which have now been
brought to the highest pitch of experimental accuracy,
namely, atomic weight determinations, density determinations
by the Retgers immersion method, and
goniometrical and physical measurements (optical and
thermal) with instruments now available of the utmost
refinement. Structural constants thus derived are
obviously of especial value. It would thus appear
that the theory requires modification so as to take
account of the experimentally proved regular increase
in volume and in the directional dimensions of the
structural unit cell of the crystal space-lattice, when
one element of the same family group and of the
same valency is interchanged for another. Indeed,
as the theory stands at present it entirely ignores
and fails to offer any explanation of the highly
important physical property of density, specific
gravity. That this physical constant, and the equally
important constant molecular volume, derived by
dividing the molecular weight by the density,
possess a real and significant meaning in isomorphous
series, formed by the interchange of elements of the
same family group, has been clearly proved in
Chapter X. This fact is, indeed, so obvious that
any further development of the theory must of
necessity take account of it.
A precise statement of their conception has
recently been made by Prof. Pope in an excellent
Report on the Progress of Crystallography, issued
289by the Chemical Society early in the year 1909.
He states that they (Pope and Barlow) “regard
the whole of the volume occupied by a crystalline
structure as partitioned out into polyhedra, which
lie packed together in such a manner as to fill the
whole of that volume without interstices. The
polyhedra can be so selected that each represents
the habitat of one component atom of the material,
and are termed the spheres of atomic influence of
the constituent atoms. Up to this point no assumption
is made other than that clearly indicated by
the result of crystallographic measurements, namely,
that each atom present in a crystalline structure
exerts a distinct morphological effect—or, what
is the same thing, appropriates a certain definite
volume. The assumption is next made that the
crystalline structure, which is resolvable into
individual molecules and ultimately into individual
atoms, exists as such by reason of equilibrium set
up between opposing attractive and repulsive
forces operating between the component atoms,
and that this equilibrium results in the polyhedra
representing the spheres of atomic influence assuming
shapes which are as nearly as possible spherical....
The polyhedra thus arrived at may be regarded as
derived by compression of a close-packed assemblage
of deformable, incompressible elastic spheres,[29]
the compression sufficing for the practical extinction
of the interstitial space. When such an assemblage
290is released from pressure it is evident that in place
of polyhedra, the shapes of which approximate as
closely as possible to the spherical, closely packed
spheres are presented; the distances between the
sphere centres can be substantially in the same
ratios as the distances between the centres of the
corresponding polyhedra in the unexpanded mass,
and the equilibrium condition of maximum sphericity
of the polyhedra will be presented in the expanded
mass of spheres by the existence of the maximum
number of contacts between spheres. The whole
method of treating the primary assumption thus
resolves itself into finding close-packed assemblages
of spheres of various sizes representing by their
relative volumes the spheres of influence of the
component atoms of any particular crystalline
structure.”
Some very interesting evidence of the validity of
their fundamental assumption of spheres of influence
of the component atoms as the ultimate structural
units is brought forward. They show that there
are two modes of closely packing equal spheres,
which give rise respectively to a cubic and a hexagonal
crystal structure, the latter having a specific
axial ratio of the vertical to the three equal equatorial
horizontal axes; and that the chemical elements
which are solids and crystallise, and the structural
units of which can naturally be assumed to be equal
spheres, being those of the similar atoms of the
same chemical element, do practically all crystallise
either in the cubic system or in the hexagonal
system with the specific axial ratio indicated by
them. The theory as it concerns chemical valency
291is obviously not affected by these interesting facts,
as the spheres of influence present are those of
the identically similar atoms of the same element.
But the theory has received considerable support
from the results of the investigation of a number
of carbon compounds, chiefly derivatives of benzene.
Thus, in spite of the very wise decision of Barlow
at the time of developing his theory of the homogeneous
partitioning of space, to keep quite clear
of attributing shape to the structural unit atoms
or molecules, and to consider them as points, he,
in common with the other contributors to that
splendid geometrical work, appears driven to consider
the question of shape when, in collaboration
with his chemical colleague, he endeavours to apply
his geometrical results to the practical problems
of chemistry. It may be inevitable that we cannot
get away from the idea of shape of the fundamental
structural units. Yet the moment we do admit
the idea, and begin to talk of polyhedra, or even of
spheres, in close or any other packing, we enter the
debatable land, concerning which the experimental
evidence is as yet but shadowy and liable to many
interpretations. Hence it is that we have the
parallelohedra of Von Fedorow, having volumes
proportional to the molecular volumes, the more
general plane-faced cell of fourteen faces, the tetrakaidecahedron
of Lord Kelvin and its deformed
derivatives, and now the polyhedra of Pope and
Barlow. The more indefinite “Fundamentalbereich”
of Schönflies appears to be left behind,
and we have embarked on a definite course of
attributing shape to the component atoms or their
292regions of influence in the crystal structure.
Von Fedorow has developed his particular theory
in a very masterly manner, and with the aid of it
professes, and with very considerable success in
many cases, to determine the correct mode of setting
up a crystal for truly comparative descriptive
purposes, and has derived therefrom a remarkable
method of crystallochemical analysis.
Moreover, there is yet another view, that of
Sollas,[30] that the packing of the molecules is a more
open one altogether, a view to which he has been
guided by consideration of the molecular volume.
Sollas has offered some remarkable explanations of
crystal structure, notably in the case of the dimorphous
forms of silver iodide. The abnormal contraction
which occurs on heating this interesting
substance, and its sudden transformation at 146° from
the ordinary hexagonal into a cubic modification as
discovered by Lehmann, appear capable of very clear
explanation on the basis of his theory. According
to this theory of Sollas the volumes of the spheres of
influence of the atoms of the different elements of
the same family group, such as those of the group
of alkali metals or those of the halogens, chlorine,
bromine, and iodine, vary progressively in a manner
which is dependent on the atomic volumes of the
elements, which have a real comparative significance
when the elements belong to the same family group.
It is probable that there is a considerable substratum
of truth behind these various apparently
conflicting views, and what is now required is that
the germ of real fact shall be winnowed from the
293husk of fallacious speculation, just as occurred in
the happy recent settlement of the old issue between
Haüy and Mitscherlich. As in that case, moreover,
it will be experimental work of superlative accuracy
which can alone offer the desirable evidence on
which a satisfactory arbitration can be founded.
It is thus obvious that we have now arrived at a
stage in the history of crystallography when more experimental
data, and many more measurements of the
most carefully conducted character, on pure materials
and excellently developed crystals, are most urgently
needed, in order to decide these important, indeed
fundamental, questions, the present state of which
the author has endeavoured to present with judicial
impartiality. When one looks around, and sees
the almost complete lack of opportunities for the
training of investigators in this rapidly growing
branch of science, the importance of which to
chemistry and physics is increasing every day,
while the field is ripe for the harvesters, one is
inclined to feel depressed with the thought of the
opportunities which are being lost. Our country
has, in this science at any rate, a fine record, having
with few breaks led the van of progress from the
time of Wollaston, the inventor in the year 1809 of
the reflecting goniometer, and of Miller, the originator
of our method of describing crystals and the pioneer
of accurate experimental work, down to the present
day. It may be, also, that our country’s reputation
is safe at this moment. But it is in the hands
of a band of investigators so small, and often of the
private and not professional nature, carrying on
the work for sheer love of it and deep interest in it,
294that the wonder is that so much has been done, and
it is the provision for carrying on our national
tradition of leadership in crystallography in the
future that is a matter for the deepest concern.
If the perusal of this book should have awakened
sufficient interest in the minds of some of its readers
to prompt them to offer themselves as recruits to
this small band of investigators, and especially if
it should have inspired the zeal and enthusiasm of a
few young students looking around for a promising
and fascinating field of work, and, finally, if it should
prove to be of assistance in obtaining the means of
training such recruits with the help of the best and
most accurate experimental apparatus which can be
obtained, the author’s main objects in writing it will
have been attained.
295
INDEX
- Airy’s spirals, 197
- Alpine snow-field, 49
- Alum, ammonium iron, 43;
- Amethyst quartz, 222–229;
- as example of pseudo-racemism, 231, 232
- Ammonium chloride labile crystallisation, 248;
- iron alum, 43;
- NH4 group, and its isomorphism with alkalies, 82, 83, 131;
- oleate, liquid crystals of, 259–263;
- oleate, twins of, 262
- Ampère’s researches on ammonia, 83
- Anatase, crystal of, 37
- Antimony oxide, dimorphism of, 87, 88
- Apatite, crystal of, 37
- Aragonite, biaxial interference figure of, 189, 190
- Armstrong and Pope on sobrerol, 153
- Arsenic oxide, crystals of, 5, 88
- Astatic systems of molecular magnets of Lehmann, 271, 272
- Asymmetric carbon atom, 144, 145
- Axes and axial planes of crystals, 51, 55, 56
- Axial ratios, 129
- Babinet’s double-wedge quartz plate, 219
- Bacteria, destruction of one enantiomorphous form by, 149
- Barium nitrate, 152
- Barker, researches on perchlorates, 123
- Barlow, discovery of remainder of 230 point-systems, 118, 119, 140;
- and Pope’s theory, 285–292
- Bartolinus, Erasmus, 17
- Benzoic acid, screen experiment on crystallisation of, 229–231
- Bergmann and Gahn’s laws of cleavage, 18
- Berzelius and Mitscherlich, atomic weights and isomorphism, 80, 82, 83, 85
- Beudant’s researches on the vitriols, 75, 76
- Biaxial crystals, 60°-prisms and refractive indices of, 162, 163, 184;
- optic axes of, 185;
- optic axial angle of, 191
- Biot’s researches on tartaric and racemic acids, 143
- Biquartze, natural and artificial, 181, 211, 214, 216, 217
- Black band of quartz twins, 216–218
- Boisbaudran, Lecoq de, 238
- Boyle, Robert, 17
- Brauns, 254
- Bravais, 114;
- Brookite, 91
- Cæsalpinus, 15
- Cæsium alum, 42
- Calcite, crystals of, 10–13, 38;
- amount of double refraction of, 174;
- in rock sections, 177, 178;
- uniaxial interference figure of, 189, 190;
- plate perpendicular to axis of, 209;
- refractive indices of, 174;
- 60°-prism of, 165, 168
- 296Calcium carbonate, three habits of crystals of, 11
- Calcium dextro-glycerate, optical activity and crystal form of, 155–160
- Carangeot’s contact goniometer, 18–20
- Carbonate, calcium, 11, 87;
- Carbonates of alkaline earths, 74
- Carbon, dimorphism of, 137
- Carbon dioxide, liquid in quartz cavities, 46
- Cavendish, 23
- Chemical significance of crystallography, 73, 283, 284;
- valency and crystalline form, 285–291
- Cholesteryl benzoate, liquid crystals of, 258;
- acetate, spherical liquid crystals of, 281, 282
- Chromate, potassium, 84
- Chromates and manganates, isomorphism with sulphates, 84
- Classes, the 32 crystal, 6, 33
- Cleavage, 17;
- Cobalt sulphate, 78
- Conditions for growth of crystals, 240, 244, 245
- Constancy of crystal angles, 6, 13, 14, 17, 23, 132
- Convergent light experiments, 186, 188
- Copper sulphate, 40, 76, 78
- Coppet, de, 238
- Crookes, Sir William, 138, 208
- Crossed-axial-plane dispersion of optic axes, 89, 94, 95;
- of ethyl triphenyl pyrrholone, 106, 107, 108;
- of gypsum, 89
- Crystal, definition of, 4;
- germs and their influence on crystallisation, 236, 237
- Crystals, modes of formation of, 4, 5
- Cube and its perfection of symmetry, 38;
- Cubic system, 37
- Cyanide, potassium cadmium, crystals of, 42
- Dalton, 25
- Dark field of polariscope, 188, 202
- Davy, Sir Humphry, researches on ammonia, 82, 83
- Delafosse and morphotropy, 101
- Deville and Troost’s researches on tantalum chloride, 84, 85
- Diamond, 8, 137, 138, 207, 208
- Dibenzal benzidine, liquid crystals of, 264
- Digonal axis of symmetry, 36
- Dimensions of structural parallelepipeda, 129
- Dimorphism, 79, 87;
- of antimony oxide, 87, 88;
- of carbonate of lime, 79, 87;
- of mercuric iodide, 97;
- of sodium dihydrogen phosphate, 80, 81;
- of sulphur, 86;
- of vitriols, 79
- Directive molecular force in crystallisation, 139, 269, 274–277
- Dog-tooth spar, 10–12
- Double refraction, interference colours due to, 176, 177;
- measure of, 169, 170;
- of biaxial crystals, 184;
- of uniaxial crystals, 183
- Double sulphates and selenates, 35, 79, 121, 127, 128, 132
- Dulong and Petit’s law, 84
- Electronic corpuscles, constituents of atoms, 113, 124
- Elements of a crystal, 68, 69
- Enantiomorphism and optical activity, 140;
- Epsom salts, 76, 78
- Ethyl triphenyl pyrrholone, 105, 106
- Eutropic series, definition of, 132
- External molecular compensation, 134, 234
- Extinction directions, 204, 205
- Fedorow, von, discovery of remainder of 230 point-systems, 118, 119, 140;
- Ferricyanide, potassium, 44
- Ferrocyanide, potassium, 43
- Ferrous sulphate, 76, 78
- Fletcher, indicatrix of, 184
- Fluorspar, single refraction of, 206
- Form, definition of a, 11, 60, 61
- Frankenheim on morphotropy, 101;
- discovery of space-lattices, 114
- Frankland and Frew, 155
- Fuchs, von, researches on sulphates of barium, strontium, and lead, 75, 77
- Fuess reflecting goniometer, 64–66
- Fundamentalbereich of Schönflies, 112, 113
- Gattermann, 258
- Gay-Lussac on alums, 77;
- on ammonia, 83;
- on racemic acid, 142
- Gernez, 238
- Gessner, 14
- Gmelin, researches on racemic acid, 142
- Goniometer, contact, 19, 20;
- Graphite, 137
- Groth, von, morphotropic researches, 98, 102–104
- Growth of a crystal, 1;
- Guglielmini, researches on crystal structure, 17
- Gypsum (selenite), cleavage of, 203;
- crystals of, 14;
- extinction directions of, 204;
- 60°-prism, experiment with, 163, 168;
- twins of in polarised light, 205, 206
- Habit of crystals, 12, 13
- Hardness of crystals, 255, 274
- Hatchett’s discovery of columbium, 85
- Haüy, 22;
- and Mitscherlich, 70, 75, 77, 88, 132;
- fundamental forms, 22, 23;
- law of constancy of form, 23;
- lattices, 29;
- law of rational indices, 24, 29, 30;
- modernisation of theories of, 30–32;
- molécules intégrantes, soustractives, and élémentaires, 25–28;
- structural units, 24
- Hemihedral classes of crystals, 34
- Hexagonal axes of symmetry, 36;
- Hexakis octahedron, 39;
- Hjortdahl and morphotropy, 101
- Holohedral classes of crystals, 34
- Homogeneity, 6, 16;
- Homogeneous structures, the 230 types of, 6, 111
- Hooke, Robert, 16
- Huyghens, 17;
- discovery of laws of double refraction, 17;
- investigation of calcite, 17
- Ice, crystalline form of, 47
- Iceland spar, discovery of, 17;
- Inactive tartaric acid, 144
- Inactivity, true optical, 235
- Indicatrix of Fletcher, 184
- Indices of crystal faces, 11
- Intercepts on crystal axes, 58
- Interference colours due to double refraction, 177;
- figures of biaxial and uniaxial crystals, 189–191
- Internal structure of crystals, 15, 111–120
- Iodide of mercury, dimorphism of, 97
- Isomerism, chemical and physical, 142, 143
- Isomorphism, Mitscherlich’s conferment of the term, 81;
- doctrine of, 81, 82;
- limitations of, 85;
- recent clearer definition of, 121–132
- Isotropic crystals, 206
- John of Berlin’s discovery of racemic acid, 142
- 298Kipping and Pope, definition of racemism and pseudo-racemism, 153, 154
- Kopp, 100
- Kundt’s powder, 149
- Labile solutions, 241
- Laurent and Nickle’s organic researches, 99
- Lavoisier, 23
- Law of rational indices, 24, 50, 57, 59
- Le Bel and van t’Hoff’s explanation of optical activity, 151
- Le Blanc, researches on alums, 77
- Lehmann, researches on liquid crystals, 256–282
- Liquid crystals, 255–282;
- and polymorphism, 138, 139;
- list of substances forming, 280, 281
- Magnesium sulphate, 76, 78
- Mallard and Le Chatelier on silver iodide, 256
- Manganate, potassium, 96
- Manganates, 84, 96
- Manganese sulphate, 78
- Marignac and isomorphism of tantalum and niobium compounds, 84;
- Mercury iodide, dimorphism of, 97
- Metastable solutions, 240
- Methyl triphenyl pyrrholone, 105, 106
- Mica-sectors plate for testing sign of optical rotation, 212, 213
- Microscope, Lehmann’s crystallisation, 256, 257, 276–280
- Miers, H. A., researches on crystallisation, 238–243;
- on red silver ores, 109;
- on vicinal faces, 248–254
- Millerian indices, 57
- Mirror-image symmetry, 118, 119, 134, 135;
- illustrated by quartz, 231
- Mitscherlich, experiment with gypsum, 90–94;
- Mixed crystals, 77, 86
- Molecular compound, racemic acid a, 150
- Molecular volume and distance ratios, 129, 130
- Molecule, individuality and directive force of, 139, 269
- Monochromatic illuminator, 192, 193
- Monoclinic system, 39;
- axes and axial planes of, 53, 54
- Morphotropy, 98–104
- Muthmann, researches on permanganates, 123
- Naphthalene tetrachloride, 99
- Newton’s seven orders of spectra, 177
- Nickel sulphate, 76, 78
- Nicol prism, 174, 175, 187
- Nitrobenzenes, von Groth’s researches on, 104
- Noble, Sir Andrew, experiments on liquefaction of carbon, 138
- Optical activity and mirror-image symmetry, 141;
- antipodes, characters of, 152;
- characters of crystals, 7
- Optically active classes of crystals, 150, 151
- Optic axes of biaxial crystals, 185;
- axis of uniaxial crystals, 165;
- axial angle, 191;
- axial angle of ethyl triphenyl pyrrholone for different wave-lengths, 107, 191;
- axial angle of gypsum at different temperatures, 90–94, 191
- Ostwald’s predictions of crystallisation phenomena, 238, 240
- Oxides of arsenic and antimony, isodimorphism of, 88
- Para-azoxy-anisol, liquid crystals of, 259, 265;
- 299-benzoic acid, 263;
- -cinnamic acid, 263;
- -phenetol, 258, 259
- Parametral form, 56
- Pasteur’s law, 155;
- research on morphotropy of tartrates, 100;
- research on tartaric and racemic acids, 142–150
- Penfield’s diagram of spherical projection, 61, 62
- Penicillium glaucum, destruction of dextro component of racemic acid, 148
- Perchlorates and permanganates, isomorphism of, 84, 96
- Pfaff, 254
- Phases, different solid, 137
- Phenol and resorcinol, von Groth’s researches on, 103
- Phosphate, ammonium magnesium, 43;
- sodium dihydrogen, dimorphism of, 80, 81
- Phosphates and arsenates, isomorphism of, 73, 74
- Phosphorus, dimorphism of, 138
- Photomicrographs of growing crystals, mode of obtaining, 41
- Pistor’s goniometer, 89
- Planeness of crystal faces, 6, 7
- Polarisation colours due to optical activity, 179
- Polarisation, rectangular, of spectra from doubly refractive prisms, 164
- Polariscope, the, 187, 188
- Polymorphism, 133–137
- Pope and Barlow, theory of, 285–291
- Positive and negative uniaxial and biaxial crystals, 166
- Potassium bichromate, metastable and labile crystallisation of, 246, 247;
- manganate, 96;
- nickel sulphate, 35;
- selenate, 96;
- sulphate, 13
- Priestley, 23
- Primitive form of Romé de l’Isle, 20, 27
- Projection polariscope, for convergent light, 92, 186, 188, 189;
- Progressive change of crystal angles in isomorphous series, 125;
- of double refraction, 126;
- of molecular distance ratios, 130, 131;
- of position of optical ellipsoid, 128
- Propyl triphenyl pyrrholone, 106, 108
- Proustite, 109, 110
- Pseudo-racemism, 153, 154
- Pyrargyrite, 109, 110
- Pyroelectrical properties of crystals, 149
- Quartz, 170;
- crystalline form of, 171, 172;
- crystals in rock sections, polarisation colours of, 175–178;
- crystals, liquid cavities in, 45;
- crystals on sand grains, 2, 3;
- double refraction of, 174;
- interference figure in convergent polarised light, 194–196;
- optical activity of, 173, 179–181, 210;
- plates, preparation of for polariscope, 181;
- polarisation colours of due to optical activity, 209, 210;
- refractive indices of, 174;
- screw point-systems of, 151;
- 60°-prism experiment with, 165, 168;
- Steno’s research on, 16;
- twinning of, 215, 216, 219–221, 225;
- two varieties of as examples of mirror-image symmetry, 171
- Racemate, sodium ammonium, Pasteur’s researches on, 147, 148
- Racemic acid, 142–146, 233, 234
- Racemic forms and racemism, 150, 153, 233
- Rammelsberg and morphotropy, 101
- Rational indices, 24, 50, 59, 116
- Reflection of light by crystal faces, 8
- Refractive index, meaning of, 167
- Reinitzer, 258
- 300Reusch’s artificial quartzes, 198, 199
- Rhombic system, 39;
- axes and axial planes of, 52, 54
- Rhombohedron and its axes, 10, 11, 54, 55, 172
- Rings and brushes, optic axial, 190, 191
- Rock-salt, cube of in quartz cavity, 45;
- 60°-prism experiment with, 162, 168
- Romé de l’Isle, 18–20;
- Roozeboom, 238
- Rotation of plane of polarisation by quartz of two varieties and different thickness, 180, 210, 211
- Royal Institution experiment with diamonds, 8
- Sal-ammoniac, 82, 83
- Salol and betol, Miers’ researches on, 242, 243
- Sand grains with quartz crystals, 3
- Scalenohedron of calcite, 11
- Scheele’s discovery of tartaric acid, 142
- Schlippe’s salt, 45
- Schönflies, discovery of remainder of 230 point-systems, 118, 119, 140
- Seebeck, researches on ammonia, 82, 83
- Selenates, isomorphous with sulphates, 96;
- Selenic acid, 95
- Selenite, polarisation colours of films of, 203
- Selenium, discovery by Berzelius, 96
- Sella’s warning against hasty generalisation, 102
- Senarmontite, 88
- Silver iodide, 256, 292
- Single refraction of cubic crystals, 162, 183
- Snow crystals, 49
- Sobrerol, 153
- Sodium chlorate, 151;
- Sohncke, regular point-systems, 117;
- mirror-image molecular arrangement, 141;
- two point-systems of quartz, 151
- Sollas, crystal structure, theory of, 292
- Solubility and supersolubility, 238–241;
- Solutions, optical activity of, 151;
- metastable and labile, 240, 241
- Space-lattices, 50, 114–116;
- triclinic illustration of, 115
- Specific gravity, importance of determinations of, 129
- Spheres of influence of atoms, 113
- Steno, 16
- Stereographic projection, 34, 62, 67;
- of topaz, 68;
- of double sulphates, 35
- Stereometric arrangement of atoms in molecule, 124, 136
- Story Maskelyne, 34
- Strain, polarisation colours of glass and diamond due to, 207, 208
- Structural units of crystals, 24, 111–113
- Sulphantimoniate of sodium, 45
- Sulphate, ammonium magnesium, 44
- Sulphates of alkalies, 121;
- of barium, strontium and lead, 74
- Sulphur, dimorphism of, 86, 87, 137;
- monoclinic form of, 4, 86
- Symbol of a face or form, 57
- Symmetry, axes and planes of, 34, 36, 41, 55;
- Systems, the crystal, 6, 7, 33
- Tartaric acid, 142–148;
- dextro, 143, 146–148;
- lævo, 144, 146–148;
- pyro-electrical properties of, 149
- Tartrate, hydrogen potassium, 43
- Tetartohedral classes of crystals, 34
- 301Tetragonal system, 37;
- axes and planes of, 36, 52
- Thallium, relation of to alkali metals, 131
- Thénard and Gay-Lussac, research on ammonia, 83
- Thomson, J. M., 238
- Thomson, Sir J. J., discovery of composition of atoms, 112
- Topaz, crystal of, 40;
- stereographic projection of, 68
- Transition tint, 180
- Triclinic bipyramid, 56;
- system, 40;
- axes and planes of, 53, 54
- Trigonal system, 37;
- axes and planes of, 37, 53, 55
- Triphenyl pyrrholone derivatives, 105–108
- Triple tartrate of sodium, potassium, and ammonium, 91
- Tutton, fixed positions of atoms in crystals, 122–124;
- law of progression of crystal properties in isomorphous series, 121–123, 129;
- nature of structural units, 134, 135;
- research on calcium dextro-glycerate, 157, 160;
- researches on simple and double sulphates and selenates, 121;
- researches on triphenyl pyrrholones, 105–108
- Uniaxial crystals, optic axis of, 165;
- 60°-prisms of, 164;
- two refractive indices of, 166, 183
- Valentinite, 88
- Vanadium family group of elements, 85
- Vauquelin, researches on alums, 77
- Vicinal faces, 248–254
- Vitriols, the, 15, 76, 78
- Von Lang, 23, 34
- Vorländer, 263;
- nature of molecules forming liquid crystals, 273
- Water, exceptional thermal dilatation of, 47
- Water flowers in ice, 47
- Water of crystallisation, 76, 78, 79
- Wave-length of most luminous part of spectrum, 179
- Werner’s fundamental form, 20
- Westfeld, 18
- Weyberg, 250
- White of higher orders, 178
- Wollaston’s reflecting goniometer, 63, 81;
- work on carbonates and sulphates of barium, strontium and lead, 74, 75
- Wulff, 250, 252, 253
- Zinc sulphate, 76, 78
- Zone of crystal faces, 63;
PRINTED BY
TURNBULL AND SPEARS,
EDINBURGH
- Silently corrected obvious typographical errors and variations in spelling.
- Retained archaic, non-standard, and uncertain spellings as printed.
- Re-indexed footnotes using numbers and collected together at the end of the last
chapter.